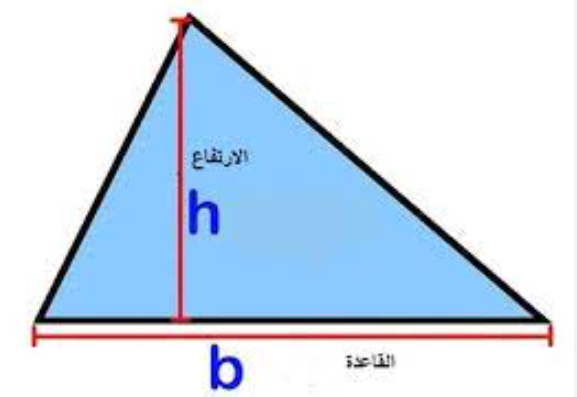
المثلثات، تلك الأشكال الهندسية البسيطة التي تتكون من ثلاثة أضلاع وثلاثة زوايا، هي مبنى أساسي لدراسة الهندسة الرياضية. ومن بين المفاهيم الأساسية التي تتعلق بها، يبرز حساب « مساحات المثلثات » كمفتاح لفهم الكثير من الظواهر الهندسية والتطبيقات العملية في حياتنا اليومية.
عندما نتحدث عن مساحات المثلثات، ندخل عالمًا من التفاصيل الرياضية الرائعة والتي تحمل في طياتها الكثير من الأسرار والتحديات. حيث يعمل حساب مساحة المثلث على توجيهنا نحو فهم أعمق للعلاقات بين أضلاع المثلث وزواياه، وكذلك كيفية تطبيق هذه المفاهيم في المجالات العلمية والهندسية.
مساحة مثلث القائم الزاوية
يُعد المثلث القائم أحد أنواع المثلثات الأساسية، حيث يحتوي على زاوية قائمة (90 درجة). يمكن حساب مساحته بسهولة باستخدام الصيغة
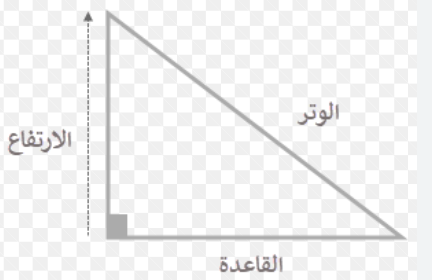
مساحة = ( 1/2) × القاعدة × الارتفاع
مثال
لدينا مثلث بضلعين معروفي القيمة 5 و 6. إذا كانت الزاوية بين هذين الضلعين 90 درجة، فكم ستكون مساحة المثلث؟
يتم الحصول على مساحة المثلث من القانون التالي:
2 ÷(ارتفاع × قاعدة) = مساحة المثلث
الصيغة الرياضية هي كما يلي:
A = b × h / 2
نعوض القيم المعروفة في القانون أعلاه:
A = 6×5 / 2
A = 30 / 2
A =15
اذاً مساحة المثلث يساوي 15
مساحة مثلث متساوي الساقين
المثلث المتساوي الساقين هو المثلث الذي يحتوي على ضلعين متساويين في الطول. ويمكن حساب مساحته إذا كان لديك قيمة كلاً من ارتفاعه وقاعدته. حساب المثلث المتساوي الساقين
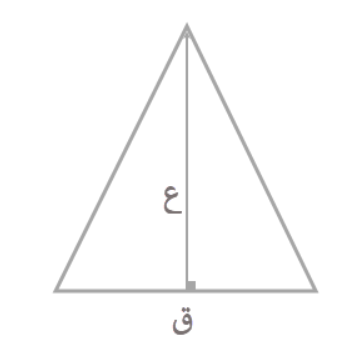
المقصود بـ ع ::: هو ارتفاع المثلث
المقصود بـ ق ::: هو قاعدة المثلث
مساحة المثلث = ( 1/2) × القاعدة × الارتفاع
مساحة مثلث متساوي الأضلاع
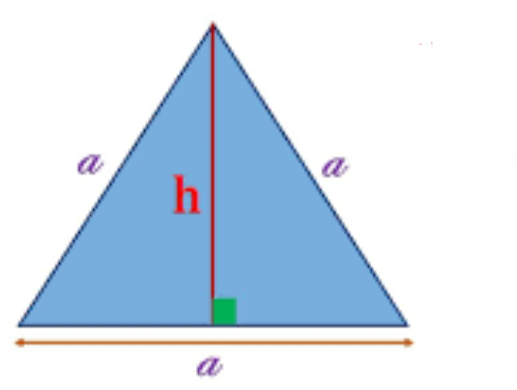
المثلث المتساوي الأضلاع هو نوع خاص من المثلثات حيث تكون جميع الأضلاع متساوية الطول. بالإضافة إلى ذلك، جميع الزوايا في هذا المثلث تكون متساوية القياس، وبالتالي، يكون لدينا زاوية متساوية القياس في كل رأس.
من أجل حساب مساحة المثلث المتساوي الأضلاع، يمكننا استخدام القاعدة التقليدية لحساب مساحة المثلث. إليك الطريقة:
مساحة المثلث = ( 1/2) × القاعدة × الارتفاع
مساحة مثلث مختلف الأضلاع
المثلث المختلف الأضلاع هو نوع من المثلثات حيث تكون أطوال الأضلاع غير متساوية. لحساب مساحة مثلث مختلف الأضلاع..