| Cours sur les nombres entiers naturels 6ème |
Nombres Entiers
I − Rang des chiffres
Définitions
Les chiffres sont 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9.
Un nombre entier est constitué de un ou plusieurs chiffres, et c’est un nombre sans virgule.
Remarque
Sur une calculatrice (ou un pavé numérique de clavier d’ordinateur), un chiffre s’obtient en appuyant sur une seule touche, alors qu’un nombre s’obtient en appuyant sur une ou plusieurs touches. Tous les chiffres sont donc aussi des nombres!
Dans un nombre, chaque chiffre occupe un certain rang détaillé dans le tableau ci-dessous
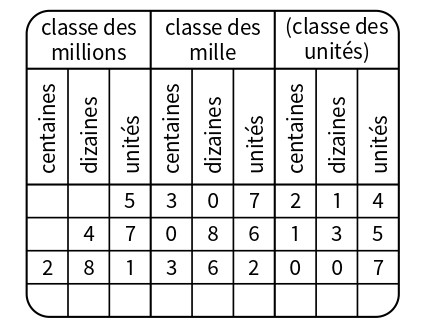
Dans le premier nombre (5 307 214) :
— 4 est le chiffre des unités,
— 7 est le chiffre des unités de mille,
— 5 est le chiffre des (unités de) millions,
— le nombre de dizaines de milliers est 530,
— le nombre de centaines est 53 072.
Dans le second nombre (47 086 135) :
— 4 est le chiffre des dizaines de millions,
— 7 est le chiffre des unités de millions,
— le nombre de dizaines est 4 708 613,
— le nombre de dizaines de mille est 4 708.
Méthode (TROUVER LE NOMBRE DE CENTAINES)
Pour trouver le nombre de centaines d’un nombre entier, il suffit d’effacer tous les chiffres dont le rang est plus petit que celui des centaines.
II − Décompositions
Définitions
N’importe quel nombre peut se décomposer :
- selon le rang de chacun de ses chiffres :
2 017 = (2 × 1000) + (0 × 100) + (1 × 10) + (7 × 1).
En effet, on écrit ici mathématiquement que 2 est le chiffre des milliers, 0 celui des centaines,
1 celui des dizaines et 7 celui des unités. De plus, puisqu’il y a un zéro dans le nombre, on aurait
aussi pu écrire plus simplement : 2017 = (2 × 1000) + (1 × 10) + (7 × 1). - en regroupant plusieurs chiffres de ce nombres ensemble :
2 017 = (20 × 100) + (17 × 1).
Dans ce cas, c’estle dernier chiffrede chaque regroupement qui donnele rang de chaque nombre :
en effet, 20 est le nombre de centaines et 17 est le nombre d’unités.
III − Écriture en toutes lettres
- 1 823 : Mille-huit-cent-vingt-trois. →pas de « s » à cent, ni à vingt car il y a encore quelque chose d’écrit arprès!
- 2 087 : Deux-mille-quatre-vingt-sept. → le mot « mille » est invariable, et toujours pas de « s » à vingt…
- 600 : Six-cents. → ici on met bien un « s » car il n’y a plus rien derrière!
- 680 : Six-cent-quatre-vingts. → pas de « s » à cent (il y a quelque chose après), mais un « s » obligatoire à vingt.
Voici les règles correspondant à ces exemples :
- Le mot « mille » est invariable; les mots « million » et « milliard » par contre s’accordent et prennent donc un s
au pluriel. - Les mots « cent » et « vingt » ne prennent un s que s’ils ne sont suivis de rien d’autre!
- Les tirets peuvent désormais être mis entre chaque mot. Avant cela, on n’en mettait que pour les portions de
nombres inférieurs à cent (par exemple pour le 2e nombre, on aurait écrit « deux mille quatre-vingt-sept »).
IV − Zéros inutiles
Propriété
Dans un nombre entier, on peut enlever les zéros qui se trouvent au début du nombre.
Exemples :
- 007 = 7 et 00 100 200 304 = 100 200 304.
- Dans 2 018, il n’y a pas de zéro inutile.
V − Demi-droite graduée
Définitions
On appelle demi-droite graduée une demi-droite qui possède une origine (toujours le zéro), un sens représenté par une flèche et une unité de longueur fixée (généralement 1 cm ou 1 carreau) :
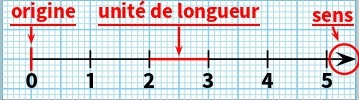
Remarque
À cette demi-droite graduée s’ajoutent lesgraduations (= nombres écrits sous la demi-droite graduée) qui doivent être régulièrement réparties!!
Propriété
Sur une demi-droite graduée,
- chaque point est représenté par un nombre appelé abscisse de ce point.
- à chaque nombre correspond un point unique.
Notation : « Le point P d’abscisse 4 » s’écrit mathématiquement « P(4) ».
Exemples :
Sur la figure suivante ,
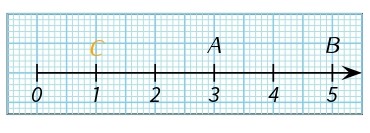
- L’abscisse du point A est 3 : A(3)
- Le nombre 5 est l’abscisse du point B : B(5)
- Où et comment placer le point C(1)?
