Les concepts Angle au Centre et Angle Inscrit sont fondamentaux en géométrie et jouent un rôle crucial dans l’étude des cercles et de leurs propriétés. Ces notions sont souvent utilisées pour décrire les relations angulaires entre différents points sur un cercle. Commençons par explorer chacun de ces concepts.
• Angle au Centre et Angle Inscrit exercice- partie1
• Angle au Centre et Angle Inscrit exercice- partie2
• Angle au Centre et Angle Inscrit exercice- partie3
Angle au Centre : Un angle au centre est un angle formé par deux rayons qui partent du centre d’un cercle et qui rejoignent deux points distincts sur la circonférence de ce cercle. En d’autres termes, l’angle au centre est l’angle formé entre les deux rayons qui relient le centre du cercle aux points de la circonférence. La mesure de cet angle au centre est égale à la moitié de l’angle correspondant au sommet du secteur circonscrit.
Angle Inscrit : Un angle inscrit est un angle formé par deux côtés d’un triangle (ou d’un polygone) et un arc de cercle correspondant à l’arc délimité par ces deux côtés. En d’autres termes, les deux côtés du triangle sont des cordes du cercle, et l’angle inscrit est l’angle formé par ces deux cordes à l’intérieur du cercle. L’angle inscrit mesure la moitié de l’angle central associé à l’arc circonscrit.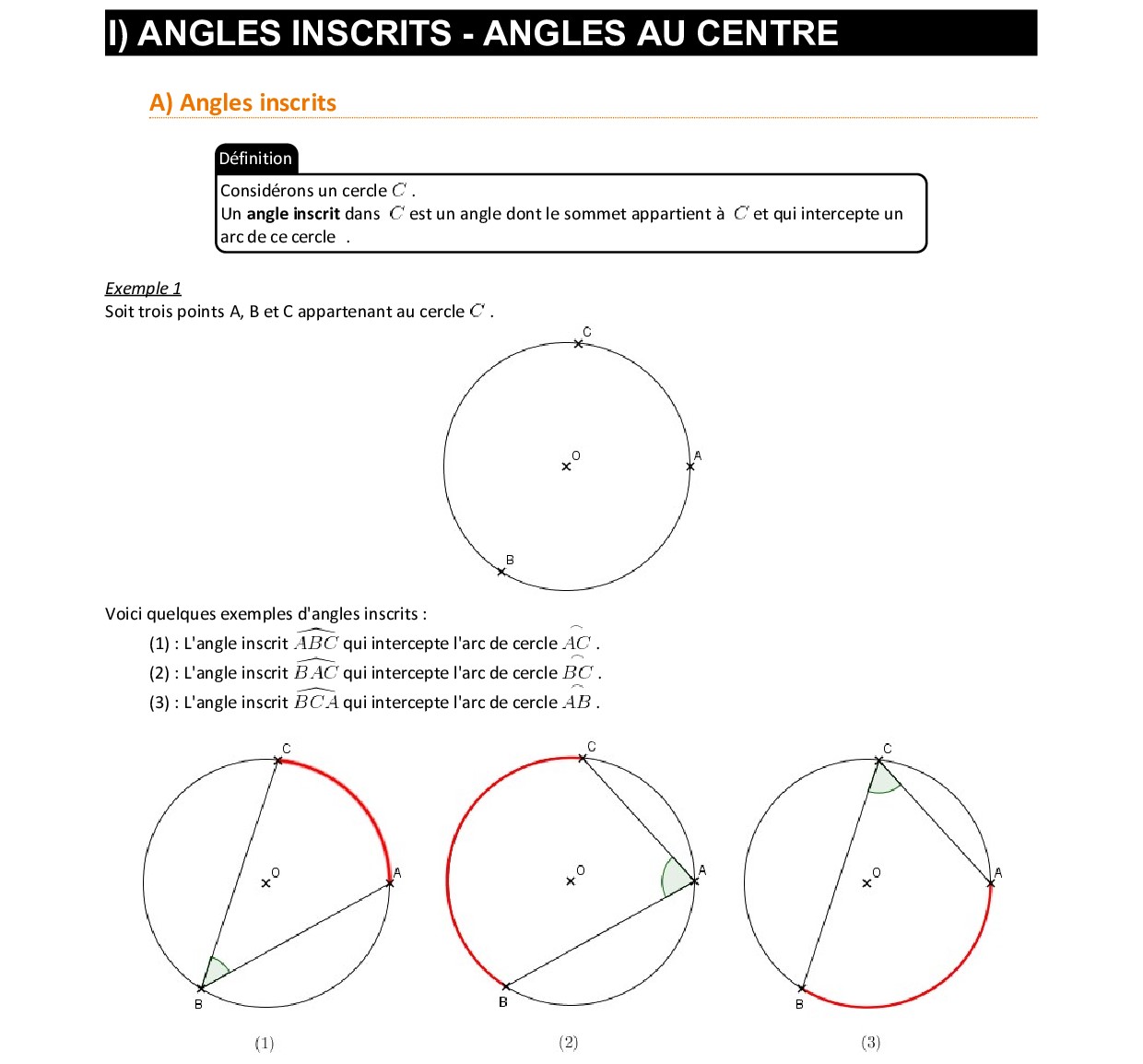

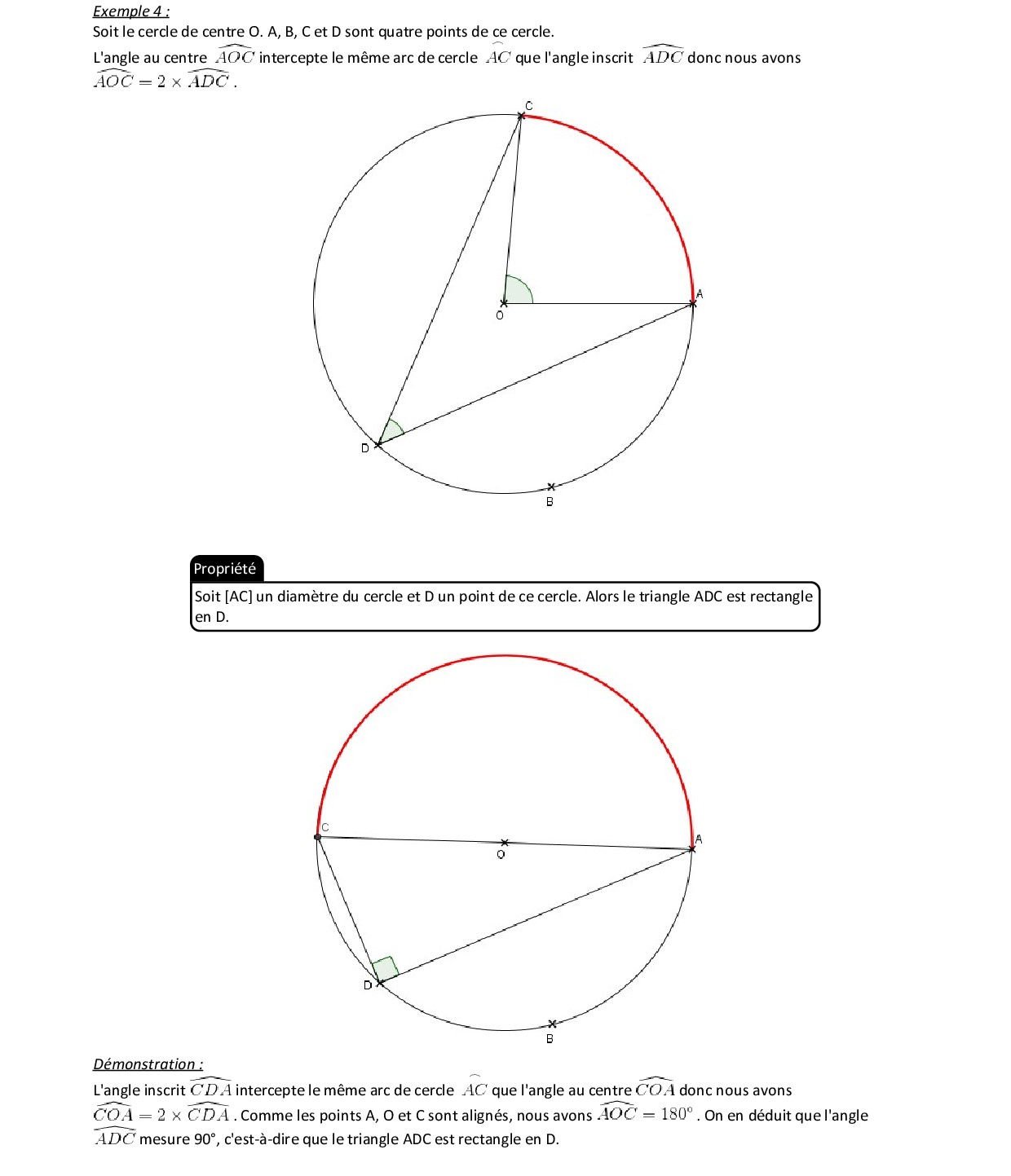
O est le centre du cercle passant par A, B et C.
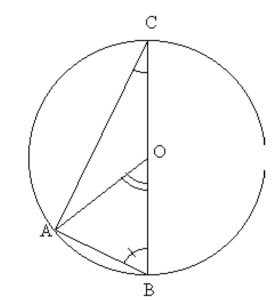
1. Sachant que ACB=25°
a) Compléter en justifiant vos réponses.
• Le triangle ABC est ……………… donc OBA= ……. -ACB =……….
• Le triangle OAB est ……………… donc OAB = ………= ……….
• La somme des angles du triangle AOB vaut …… donc AOB = …….
b) Comparer AOB et ACB : …………………………..
O est le centre du cercle passant par A, B et C.
1. Sachant que ACB=25°
a) Compléter en justifiant vos réponses.
• Le triangle ABC est rectangle donc OBA= 90° -ACB=90°-25°=65°
• Le triangle OAB est isocèle en O donc OAB = OBA = 65°.
• La somme des angles du triangle AOB vaut 180° donc :
AOB = 180°-OAB-OBA =180-65-65 = 50° .
b) Comparer AOB et ACB : ACB = 2× AOB
O est le centre du cercle passant par A, B et C.
Nous avons posé ACB = x .
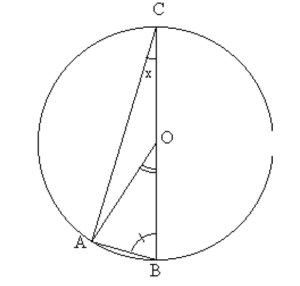
Calculer à l’aide de x :
OBA =…………………………………
OAB =…………………………………
AOB =…………………………………
O est le centre du cercle passant par A, B et C.
Nous avons posé ACB = x .

Calculer à l’aide de x :
Le triangle ABC est rectangle donc : OBA= 90°- ACB = 90°- x
Le triangle OAB est isocèle en O donc OAB = OBA =90°- x
La somme des angles du triangle AOB vaut 180° donc :
AOB =180 -OAB -OBA =180 – (90 – x)– (90 – x) = 180 – 90 + x– 90 + x = 2x
O est le centre du cercle passant par A, B et C, et ACB = 65°
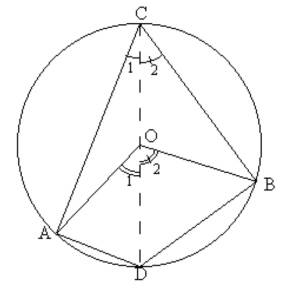
1. Sachant que ACD =25°
a) Compléter en justifiant vos réponses
DCB = ………………………………………
AOD = ………………………………………
DOB= ………………………………………
AOB = ………………………………………
b) Comparer AOB et ACB : …………………………………………
O est le centre du cercle passant par A, B et C, et ACB = 65°
1. Sachant que ACD =25°
a) Compléter en justifiant vos réponses :
Les angles ACD et DCB sont adjacents :
DCB = ACB – ACD = 65 – 25 = 40°
Les angles ACD et AOD sont construits sur le même arc BD :
AOD = 2× ACD = 2×25 = 50°
Les angles DCB et DOB sont construits sur le même arc BD :
DOB= 2×DCB = 2×40 = 80°
Les angles AOD et DOB sont adjacents :
AOB = AOD+DOB = 50+80 =130°
b) AOB et ACB : On vérifie bien que : AOB = 2× ACB
Rappel : si (BT) est tangente au cercle alors (BT) est
perpendiculaire à (OB). C’est le cas ici.
Sachant que BOC = 100°
Compléter en justifiant vos réponses :
OBC+ …………. + …………. =180°
or : OBC = ………..
donc : OBC = ……………………………………………………
ainsi : TBC = 90 -………. = …………………………………..
Rappel : si (BT) est tangente au cercle alors (BT) est perpendiculaire à
(OB).
Sachant que BOC = 100°
Compléter en justifiant vos réponses :
La somme des angles du triangle BOC vaut 180° et le triangle
BOC est isocèle en O.
OBC+ BOC+ BCO =180°
or : OBC = BCO
donc : OBC =(180 – BOC)/2 = (180 – 100)/2 = 80/2 = 40°
Ainsi : TBC = 90 – OBC = 90- 40 = 50°
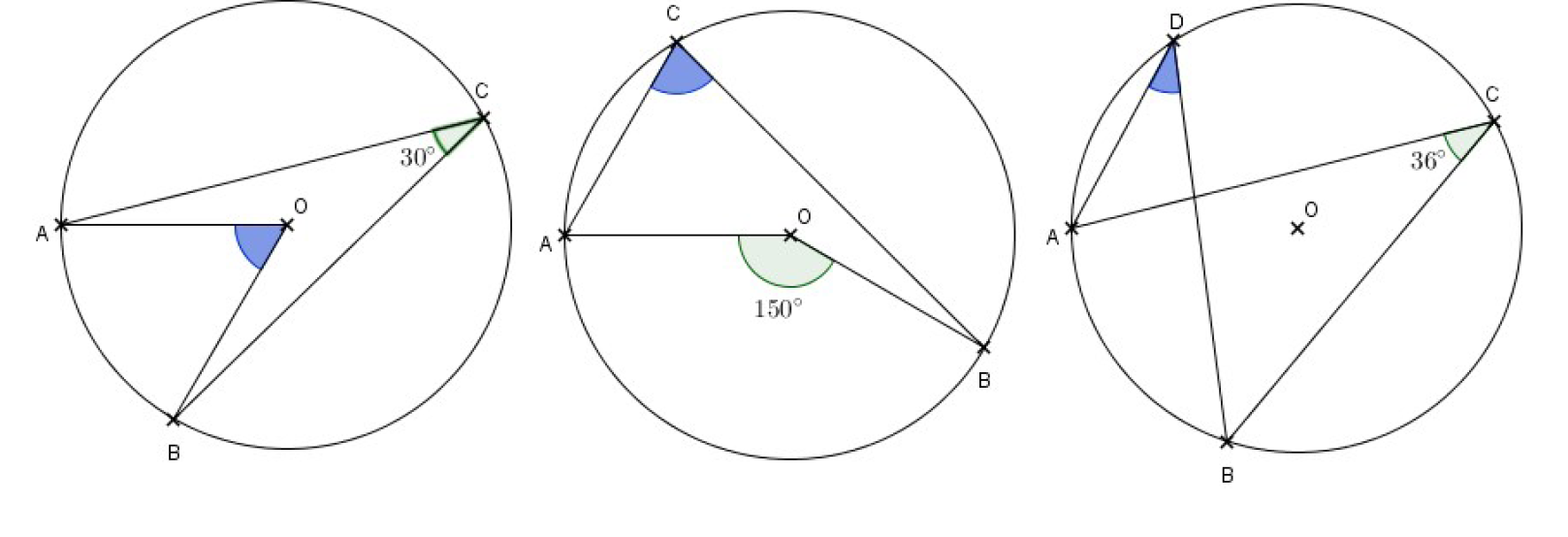
1-Pour chacune des figures, donner la mesure de l’angle ACB :
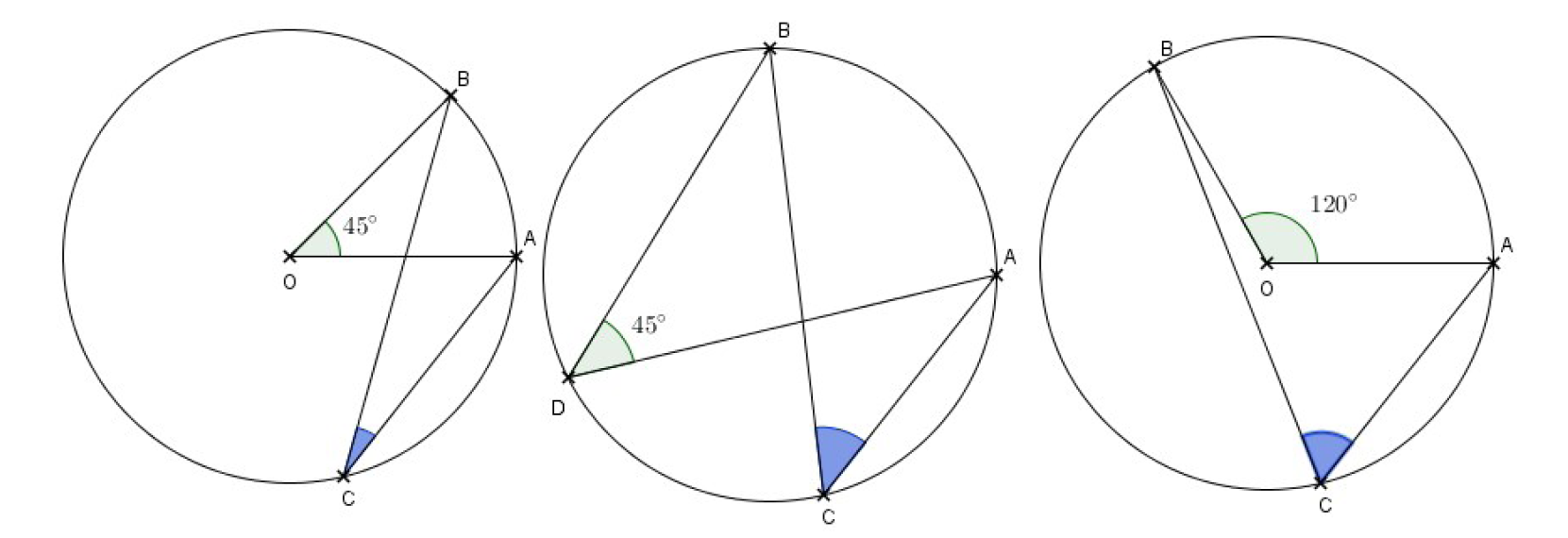
2- Pour chacune des figures, donner la mesure de l’angle colorié en bleu :
1-Pour chacune des figures, donner la mesure de l’angle ACB :

2- Pour chacune des figures, donner la mesure de l’angle colorié en bleu :

Soit (C) le cercle de centre O et de rayon [OA]. B et C sont des points de ce cercle. On donne également ACB = 30° .
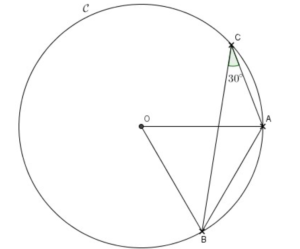
Quelle est la nature du triangle AOB ?
Les points A et B appartiennent au cercle de centre O donc nous avons OA = OB et le triangle OAB est isocèle en O.
D’autre part, l’angle au centre AOB intercepte le même arc AB de cercle que l’angle inscrit ACB donc nous avons :
AOB = 2×ACB = 2×30 = 60°
AOB mesure 60°.
Le triangle AOB est isocèle et possède en plus un angle de 60° ; par conséquent il est équilatéral.
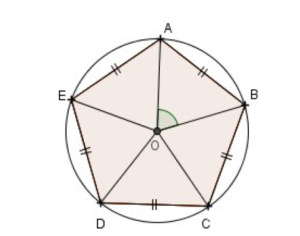
1) On considère les polygones réguliers suivants :
a) Le carré :
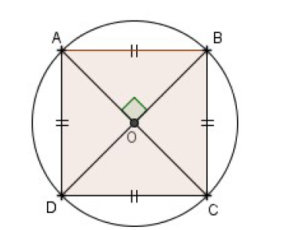
Expliquer pourquoi l’angle mesure 90°.
b) Le pentagone régulier :
Expliquer pourquoi l’angle mesure 72°.
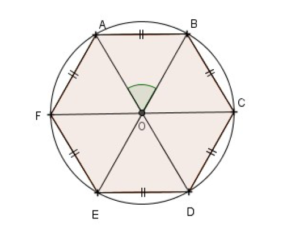
c) L’hexagone régulier :
Calculer la mesure de l’angle .
2) Un polygone régulier a des côtés de longueur 5 cm. Les angles à chaque sommet mesurent 140°.
Calculer le périmètre de ce polygone.
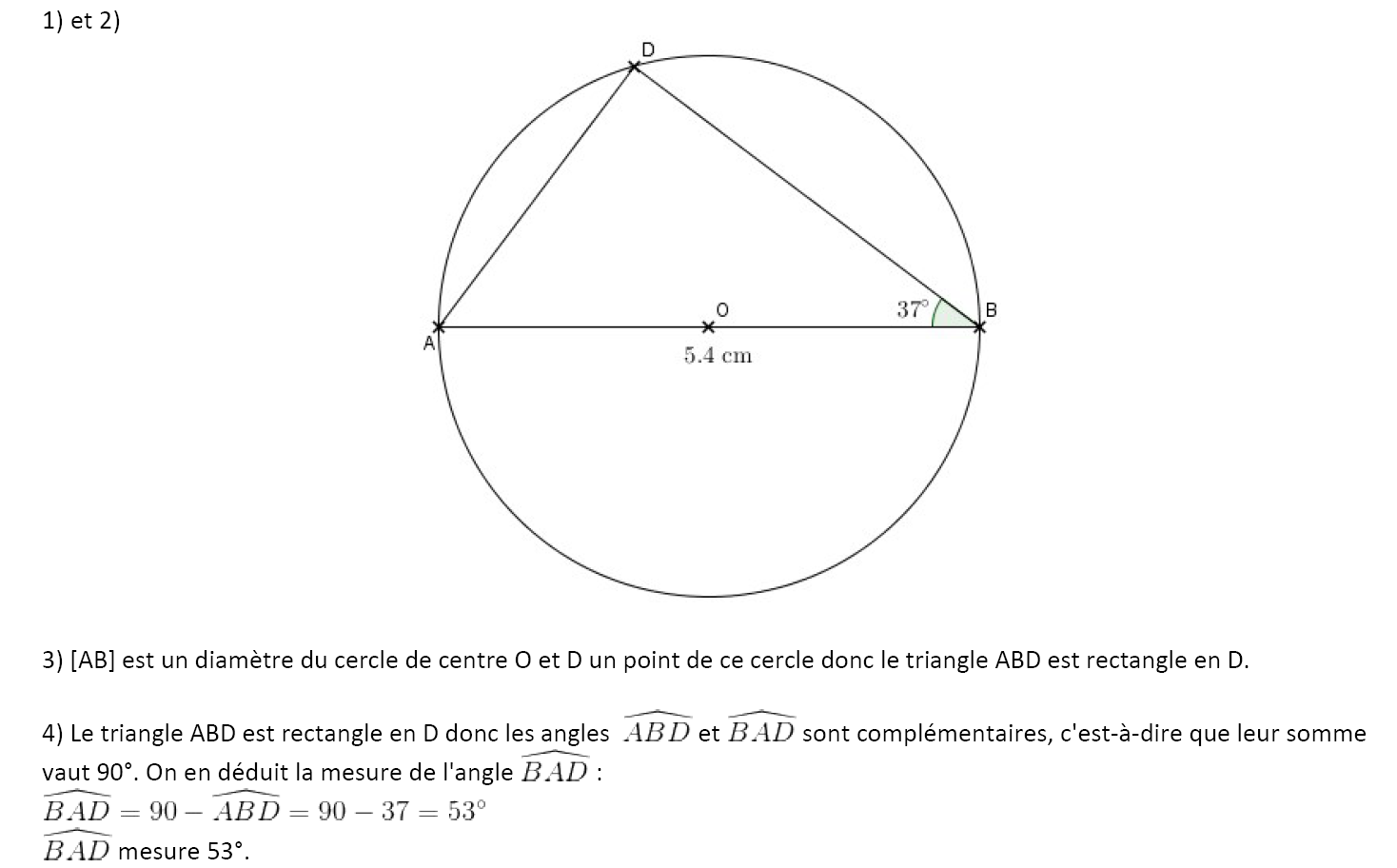
1) Tracer un cercle G de centre O et de diamètre [AB] tel que AB = 5,4 cm.
2) Construire un point D du cercle tel que ABD = 37°.
3) Quelle est la nature du triangle ABD? Justifier votre réponse.
4) Quelle est la mesure de l’angle BAD ? Justifier votre réponse.
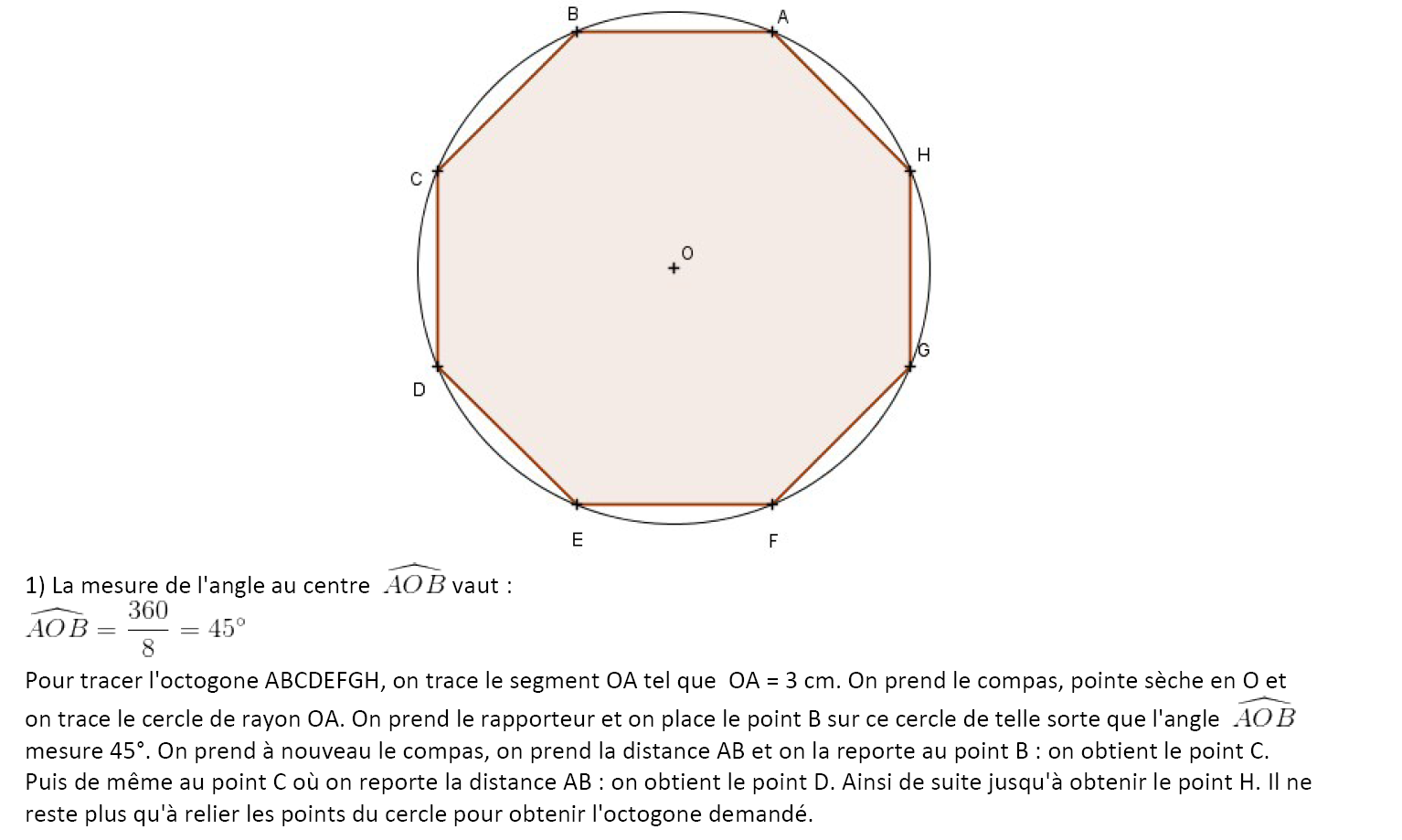
Voici un octogone régulier ABCDEFGH.
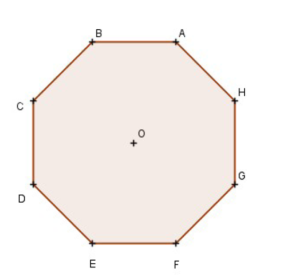
1) Représenter un agrandissement de cet octogone en l’inscrivant dans un cercle de rayon 3 cm. Aucune justification n’est attendue pour cette construction.
2) Démontrer que le triangle DAH est rectangle.
3) Calculer la mesure de l’angle BEH .
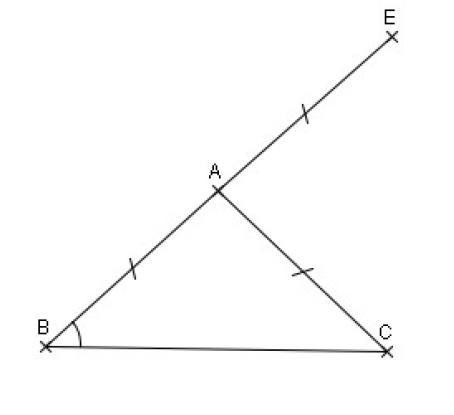
Dans cet exercice, on étudie la figure ci‐dessous où :
‐ ABC est un triangle isocèle tel que AB = AC = 4 cm
‐ E est le symétrique de B par rapport à A.
PARTIE 1
On se place dans le cas particulier où la mesure de ABC est 43 °.
1) Construire la figure en vraie grandeur.
2) Quelle est la nature du triangle BCE ? Justifier.
3) Prouver que l’angle EAC mesure 86 °.
PARTIE 2
Dans cette partie, on se place dans le cas général où la mesure de ABC n’est pas donnée.
Ali affirme que pour n’importe quelle valeur de ABC , on a : EAC = 2× ABC.
Ali a‐t‐il raison ? Faire apparaître sur la copie la démarche utilisée.
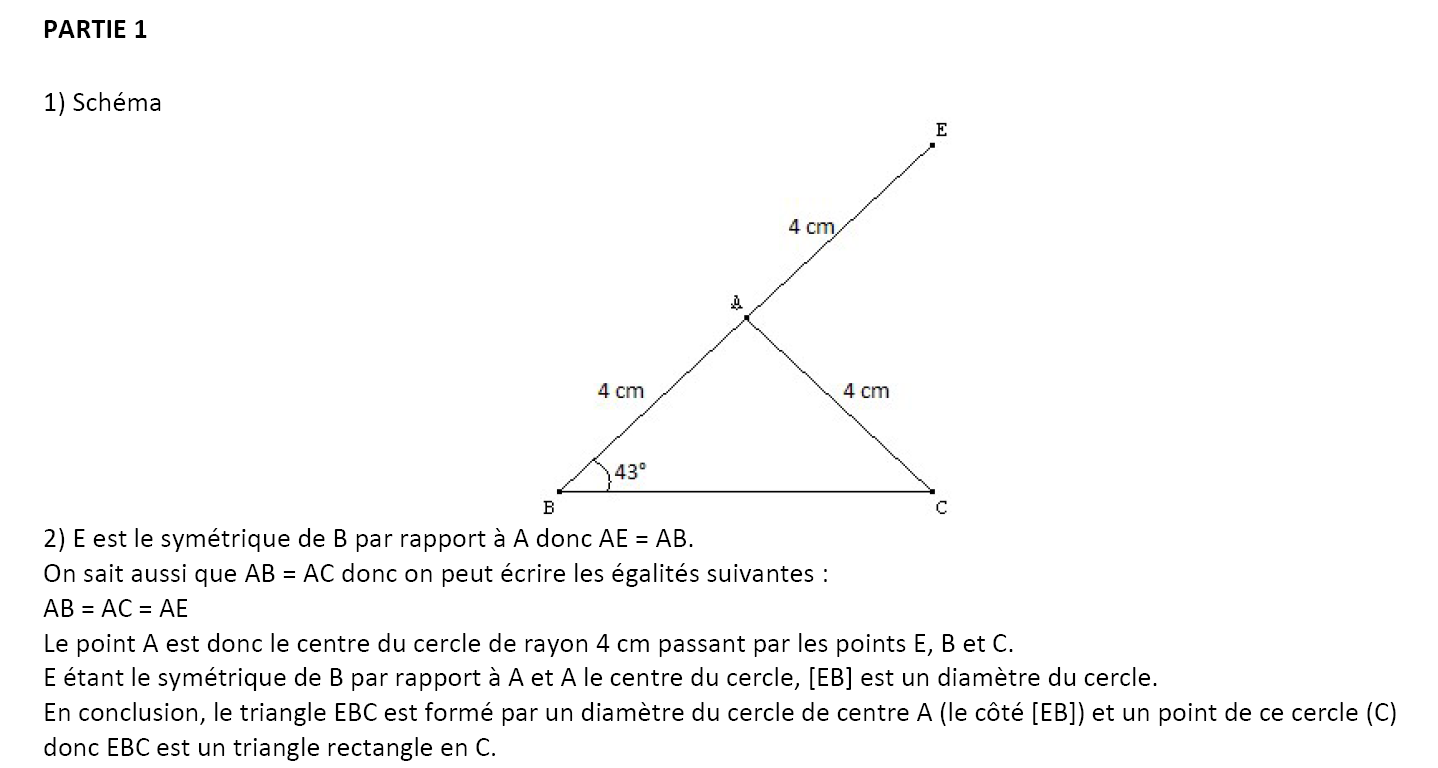

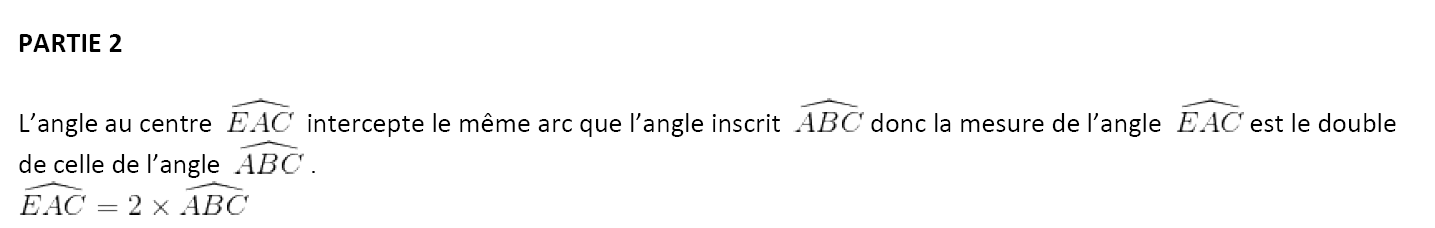
Donc Ali a raison.