Angles formés par deux droites parallèles et une sécante exercices corrigés
Exercice 1:
Les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont coupées par la sécante $(d)$.
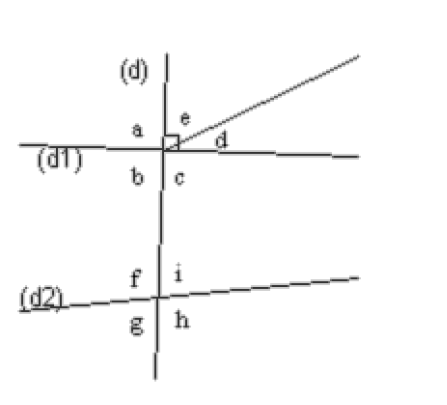
Complète les phrases suivantes en utilisant la figure :
• Les angles $g$ et $i$ sont ……………………………………
• Les angles $b$ et $c$ sont ………………………………….. et ……………………………………….
• Les angles $a$ et $f$ sont ………………………………………
• Les angles $i$ et $b$ sont ……………………………………….
• Les angles $e$ et $d$ sont ………………………………….. et ……………………………………….
• Les angles $g$ et $i$ sont opposés par le sommet.
• Les angles $b$ et $c$ sont adjacents et supplémentaires.
• Les angles $a$ et $f$ sont correspondants.
• Les angles $i$ et $b$ sont alternes-internes.
• Les angles $e$ et $d$ sont adjacents et complémentaires.
Exercice 2:
On suppose que, sur la figure ci-contre, les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles et que $\widehat{BAC} = 70°$.
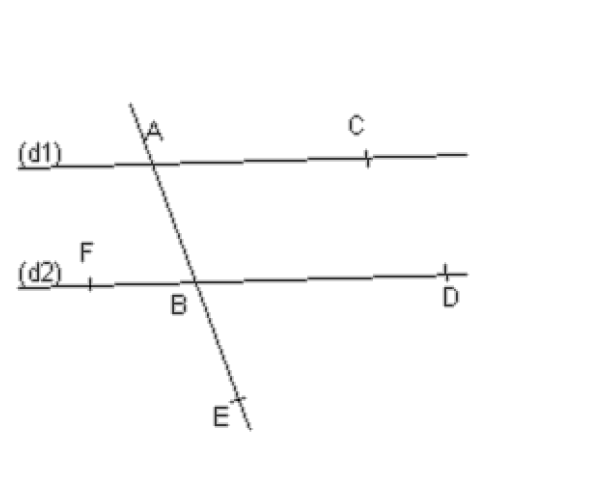
$1)$ Déterminer l’angle $\widehat{ABF} $. Justifie ta réponse.
$2)$ Déterminer l’angle $\widehat{EBD} $. Justifie ta réponse.
$3)$ Déterminer l’angle $\widehat{EBF } $. Justifie ta réponse.
$1)$ Les angles $\widehat{A B F}$ et $\widehat{B A C}$ sont alternes-internes et les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
Or si deux droites parallèles sont coupées par une sécante, alors deux angles alternes-internes ont la même mesure.
Donc: $\widehat{A B F}=\widehat{B A C}=70^{\circ}$.
$2)$ Les angles $\widehat{E B D}$ et $\widehat{B A C}$ sont correspondants et les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
Or si deux droites parallèles sont coupées par une sécante, alors deux angles correspondants ont la même mesure.
Donc : $\widehat{E B D}=\widehat{B A C}=70^{\circ}$.
Autre méthode : Les angles $\widehat{A B F}$ et $\widehat{E B D}$ sont opposés par le sommet.
Or deux angles opposés par le sommet ont la même mesure donc $\widehat{E B D}=\widehat{A B F}=70^{\circ}$.
$3)$ Les angles $\widehat{E B F}$ et $\widehat{E B D}$ (ou $\widehat{E B F}$ et $\widehat{A B F}$ ) sont supplémentaires.
Donc $\widehat{E B F}=180^{\circ}-\widehat{E BD}=180^{\circ}-70^{\circ}=110^{\circ}$.
Exercice 3:
Les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont coupées par la droite $(xy)$.
On sait que $\widehat{B A D}=82^{\circ}$ et $\widehat{EBy}=98^{\circ}$ .
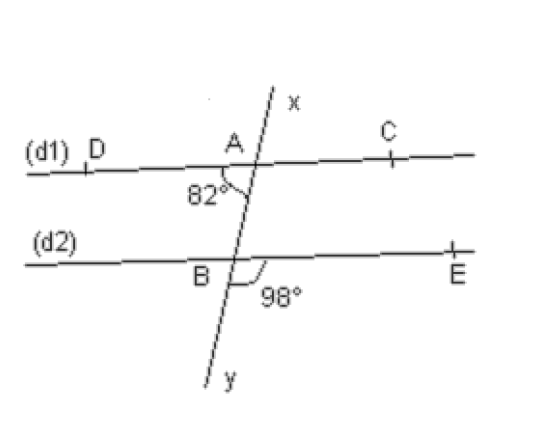
$1)$ Calculer l’angle $\widehat{ABE}$.
$2)$ En déduire que les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
$1)$ Les angles $\widehat{A B E}$ et $\widehat{E B y}$ sont supplémentaires. Donc $\widehat{A B E}=180^{\circ}-98^{\circ}=82^{\circ}$.
$2)$ Les angles $\widehat{B A D}$ et $\widehat{A B E}$ sont alternes-internes et de même mesure.
Or si deux droites coupées par une sécante forment deux angles alternes-internes de même mesure, alors ces deux droites sont parallèles.
Donc les droites $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
Exercice 4:
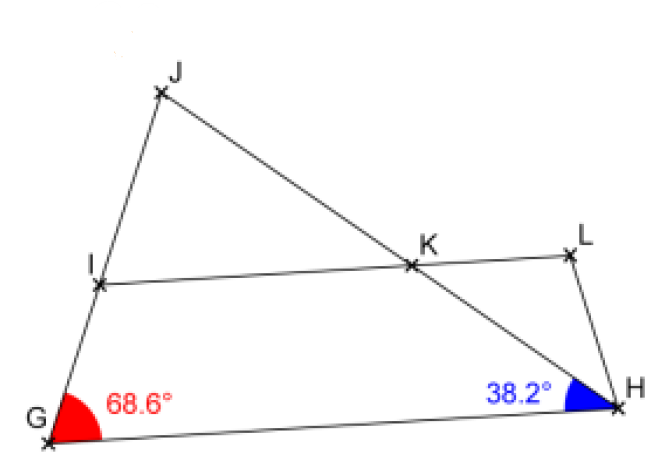
On sait que :
– les droites $(I L)$ et $(G H)$ sont parallèles ;
– les points $I, K$ et $L$ sont alignés dans cet ordre ;
– les points $J, I$ et $G$ sont alignés dans cet ordre ;
– les points $J, K$ et $H$ sont alignés dans cet ordre.
A l’aide des mesures portées sur la figure et des informations données ci-dessus, donner la mesure des angles $\widehat{K I J}, \widehat{K I G},\widehat{IKJ},\widehat{JKL} , \widehat{IK H}$ et $\widehat{L K H}$.
• Calculons la mesure de l’angle $\widehat{K I J}$.
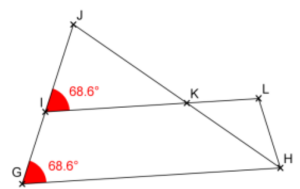
Les droites $(H K)$ et $(G H)$ sont parallèles et elles sont coupées par la droite ( $\mathcal{G}$ ) donc elles forment des angles correspondants de même mesuré.
Or, comme les angles $\widehat{H G} I$ et $\widehat{K I J}$ sont correspondants, il en résulte que $\widehat{K I J}=\widehat{H G I}=68,6^{\circ}$
L’angle $\widehat{K I J}$ mesure $68, 6^{\circ}$.
• Calculons la mesure de l’angle $\widehat{K I G}$.
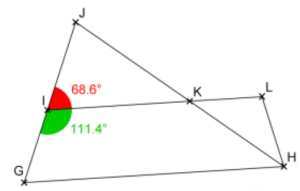
Les points $J, I$ et $G$ sont alignés dans cet ordre donc l’angle $\widehat{J I G}$ est un angle plat. Autrement dit, $\widehat{JIG}=180^{\circ}$.
En outre, les angles $\widehat{K I J}$ et $\widehat{K I G}$ sont adjacents car ils ont le même sommet $I$, le même côté commun $[K I]$ et se situent de part et d’autre de ce côté commun.
Ainsi,$\widehat{K I J}+\widehat{K I G}=\widehat{JIG}=180^{\circ}$ (autrement dit, les angles $\widehat{K I J}$ et $\widehat{K I G}$ sont supplémentaires).
Par conséquent, en remplaçant par les mesures connues, on a :
$\widehat{K I G}=\widehat{J I G}-\widehat{K I J}=180-68,6=111,4^{\circ}$
L’angle $\widehat{K I G}$ mesure $111, 4°$
• Calculons la mesure de l’angle $\widehat{IKJ}$.
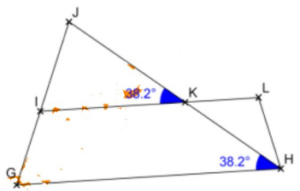
Comme les droites $(IL)$ et $(G H)$ sont parallèles et coupées par la droite $(JH)$ , elles forment des angles correspondants de même mesure.
Les angles $\widehat{IKJ}$ et $\widehat{GHK}$ étant correspondants, on a :
$\widehat{IKJ}=\widehat{KHG}=38,2^{\circ}$
L’angle $\widehat{IKJ}$ mesure $38, 2^{\circ}$.
• Calculons la mesure de l’angle $\widehat{JKL}$.
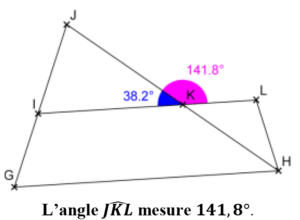
Les points $I, K$ et $L$ sont alignés dans cet ordre.
Par conséquent, l’angle $\widehat{IKL}$ est un angle plat.
De plus, les angles $\widehat{IKJ}$ et $\widehat{JKL}$ sont adjacents car ils ont le même sommet $K$, le même côté commun $[K J]$ et se situent de part et d’autre de ce côté commun.
De ce fait, $\widehat{IKJ}+\widehat{JKL}=\widehat{IKL}=180^{\circ}$ (ce quí signifie en d’autres termes que les angles $\widehat{IKJ}}$ et $\widehat{JKL}$ sont supplémentaires).
Il s’ensuit, en remplaçant par les mesures connues, que :
$\widehat{JKL}=\widehat{IKL}-\widehat{IKJ}=180-38,2=141,8^{\circ}$
L’angle $\widehat{JKL}$ mesure $141, 8^{\circ}$.
• Calculons la mesure de l’angle $\widehat{IKH}$.
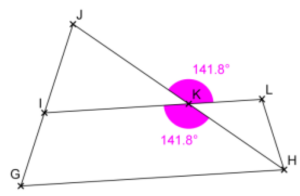
Les angles $\widehat{JKL} $ et $\widehat{IKH} $ sont opposés par le sommet donc ils ont même mesure.
On a donc $\widehat{IKH} =\widehat{JKL}=141,8^{\circ}$
L’angle $\widehat{I K H}$ mesure $141,8^{\circ}$.
• Calculons la mesure de l’angle $\widehat{L K H}$.
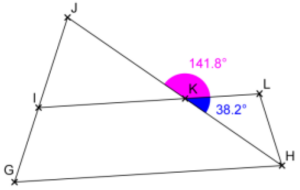
Les points $J, K$ et $H$ sont alignés dans cet ordre.
Donc l’angle $\widehat{J K H}$ est un angle plat.
Les angles $\sqrt{K K}$ et $\widehat{L K H}$ sont adjacents et supplémentaires puisque $\widehat{J KL}+\widehat{L K H}=\widehat{J K H}$.
Il vient alors que : $\widehat{L K H}=\widehat{J K H}-\widehat{JK L}=180-141,8=38,2^{\circ}$
L’angle $\widehat{L K H}$ mesure $38,2^{\circ}$.
Il peut exister plusieurs démonstrations possibles. Quelle que soit la méthode utilisée, il convient de détailler la rédaction pour montrer au correcteur que les savoirs (définitions, propriétés…) et les savoir-faire sont parfaitement maitrisés.
Exercice 5:
Dans chacun des quatre cas suivants, dire si les droites $(CF)$ et $(DE)$ sont parallèles. Justifier.
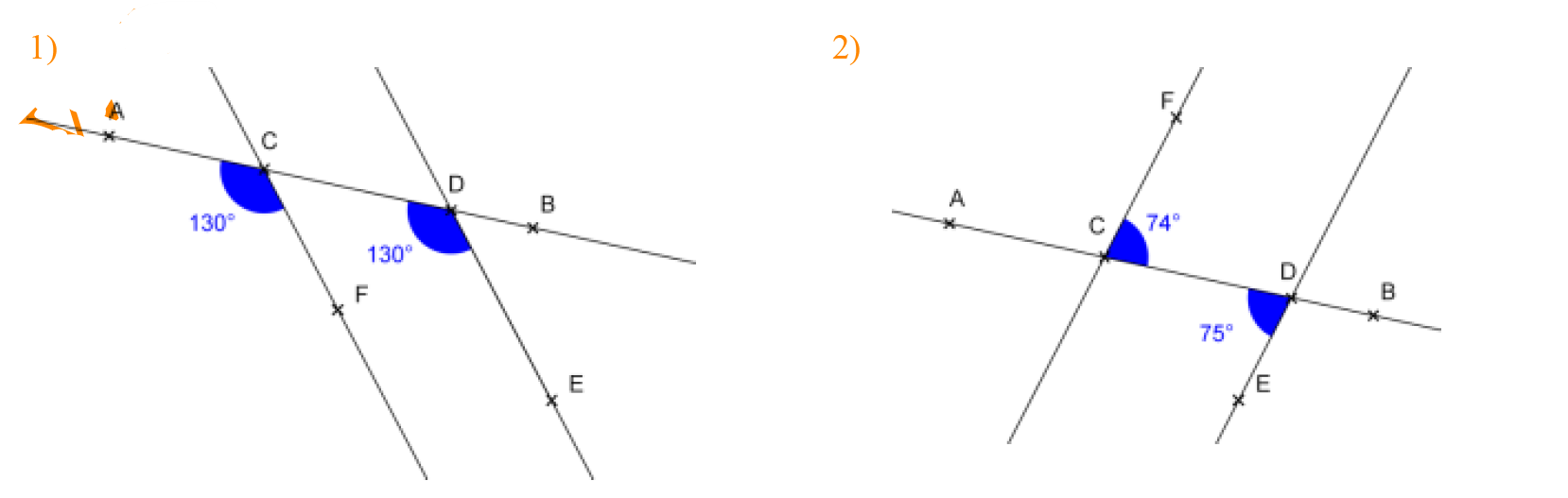
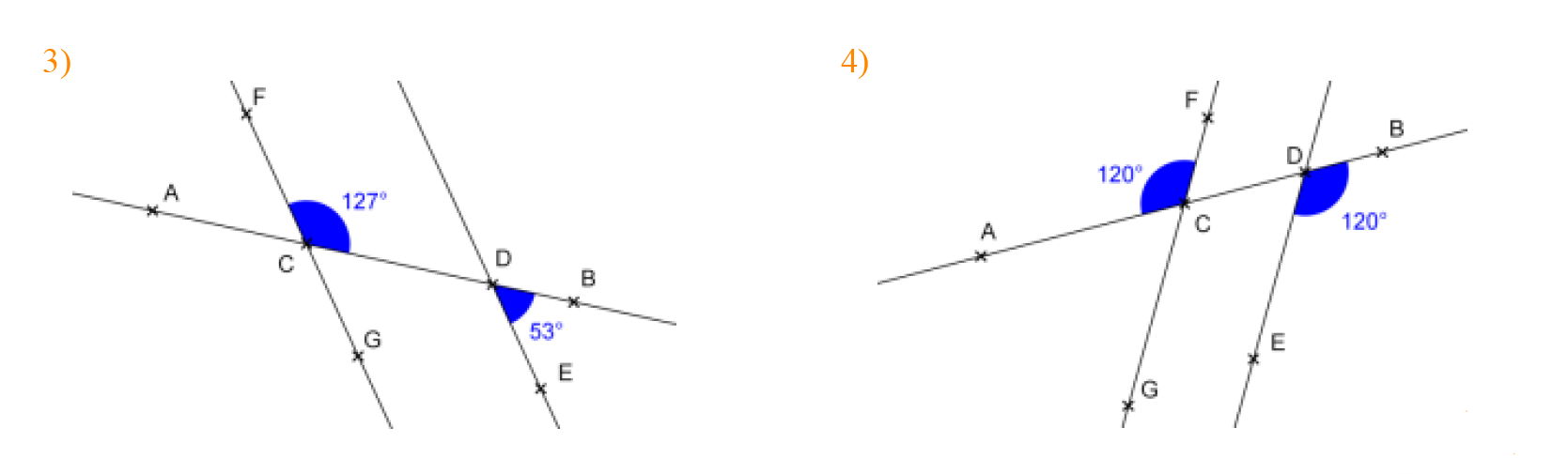
$1)$ D’apres le dessin, les angles $\widehat{A C F}$ et $\widehat{C D E}$ sont des angles correspondants.
De plus, $\widehat{A C F}=\widehat{C D E}=130^{\circ}$.
Ainsi, les droites ( $C F$ ) et ( $D E$ ) coupées par la sécante ( $A B$ ) forment des angles correspondants de même mesure.
Il s’ensuit que les droites ( $C F$ ) et (DE) sont parallèles.
$2)$ D’après le dessin, les angles $\widehat{D C F}$ et $\widehat{C D E}$ sont des angles alternes-internes.
De plus, $\widehat{D C F} \neq \widehat{C D E}$.
Ainsi, les droites ( $C F$ ) et ( $D E$ ) coupées par la sécante ( $A B$ ) forment des angles alternes-internes de mesures différentes.
Par conséquent, les droites ( $C F$ ) et ( $\boldsymbol{D E}$ ) ne sont pas parallèles.
$3)$ Les points $F, C$ et $G$ sont alignés dans cet ordre donc les angles $\widehat{F C D}$ et $\widehat{D C G}$ sont des angles adjacents et supplémentaires.
On a donc: $\widehat{F C D}+\widehat{D C G}=180^{\circ}$
D’où : $\widehat{D C G}=180-\widehat{F C D}=180-127=53^{\circ}$
On a donc $\widehat{D C G}=\widehat{B D E}=53^{\circ}$.
Par ailleurs, les angles $\widehat{D C G}$ et $\widehat{B D E}$ sont correspondants.
En conséquence, les droites ( $C F$ ) et ( $D E$ ) sont parallèles.
$4)$ Les angles $\widehat{A C F}$ et $\widehat{G C D}$ sont opposés par le sommet donc ils sont de même mesure.
Ainsi, on a $\widehat{A C F}=\widehat{G C D}=120^{\circ}$
On a donc finalement $\widehat{G C D}=\widehat{E D B}=120^{\circ}$.
Or, les angles $\widehat{G C D}$ et $\widehat{E D B}$ sont des angles correspondants.
Autrement dit, les angles $\overline{G C D}$ et $\widehat{E D B}$ sont correspondants et de même mesure.
Par conséquent, les droites $(CF)$ et $(DE)$ sont parallèles.
Exercice 6:
Sur le schéma ci-contre, les droites (AB) et (CD) sont parallèles.
Calculer les angles $E \hat{A} B, E \hat{B} A, A \hat{D} C, B \hat{C} D$ et $D \hat{E} C$.
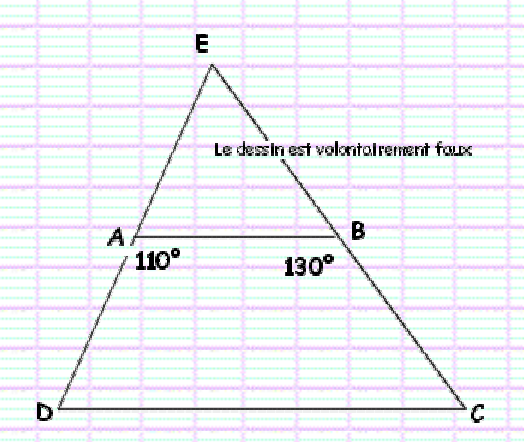
• Calcul de l’angle $E \hat{A} B$ :
Les angles $E \hat{A} B$ et $B \hat{A} D$ sont supplémentaires ( les points E, A et D sont alignés )
Donc : $E \hat{A} B = 180 – B \hat{A} D = 180 – 110 = 70°$
• Calcul de l’angle $E\hat{B}A$ :
Les angles $E \hat{B}A$ et $A\hat{B}C$ sont supplémentaires .
Donc : $E \hat{B}A = 180 – A \hat{B} C = 180 – 130 = 50°$
• Calcul de l’angle $A\hat{D}C$ :
Les angles $E \hat{A}B$ et $A\hat{D}C$ sont correspondants .
Comme les droites $(AB)$ et $(DC)$ sont parallèles (voir énoncé), ces angles ont même mesure.
Donc : $A\hat{D}C = E \hat{A}B =70°$
• Calcul de l’angle $B\hat{C}D$ :
les droites $(AB)$ et $(DC)$ sont parallèles.
Les angles $E \hat{B}A$ et $B\hat{C}D$ sont correspondants, alors ces angles ont même mesure.
Donc : $B\hat{C}D = E \hat{B}A= 50°$
• Calcul de l’angle $D\hat{E}C$ :
Dans le triangle EDC ( ou dans le triangle EAB ), la somme des angles est égale à 180 °.
Donc : $D\hat{E}C = 180 – ($E\hat{D}C + $D\hat{C}E ) = 180 – ( 70 + 50 ) = 180 – 120 = 60°$
Exercice 7:
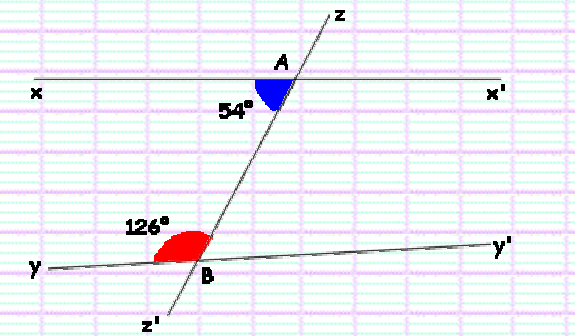
Les droites $(xx’)$ et $(yy’)$ sont-elles parallèles ?
– Les angles $x \hat{A} B$ et $A \hat{B} y^{\prime}$ sont des angles alternes-internes.
– $x \hat{A B}=A \hat{B} y^{\prime}=54^{\circ}$ donc les angles $x \hat{A B}$ et $A \hat{B} y^{\prime}$ ont même mesure.
Donc les droites ( $x x^{\prime}$ ) et ( $y y^{\prime}$ ) sont parallèles.
Exercice 8:
$1)$ Tracer $x \hat{O} y$ un angle de $120^{\circ}$, puis sa bissectrice $[Oz]$.
$2)$ Placer sur $[\mathrm{Oz})$ un point $A$ et sur $[O y)$ un point $B$ tel que $O A=O B$.
$3)$ Calculer les angles du triangle $O A B$
$4)$ Prouver que la droite ( $A B$ ) et la demi-droite $[Ox)$ sont parallèles.
$1)$ $2)$
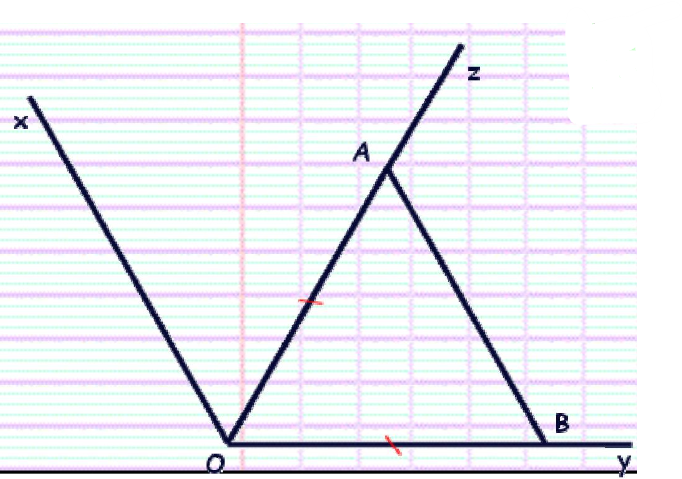
$3)$ Calcul de AÔB (et de $\times \hat{O} A$ ) : La demi-droite $[Oz)$ est la bissectrice d’e l’angle $xÔy$
Donc: $\hat{A} \hat{O} B=x \hat{O} A=x \hat{O} y: 2=120: 2=60^{\circ}$
$\triangleright$ Calcul de $O \hat{A} B$ (et de $O \hat{B A}$ ): Comme $O A=O B$ (voir énoncé ), le triangle $O A B$ est isocèle en $0$ .
Donc, comme dans un triangle isocèle, les angles à la base ont même mesure, nous avons : $O \hat{A} B=O \hat{B A}=(180-60): 2=120: 2=60^{\circ}$
En conclusion, nous avons $\hat{A} \hat{O} B=O \hat{A} B=O \hat{B} A=60^{\circ}$
(Le triangle $O A B$ est donc un triangle équilatéral)
$4)$ Les angles $B \hat{A} O$ et $X \hat{O} A$ sont alternes internes.
De plus $B \hat{A} O=60^{\circ}$ et $x \hat{O} A=60^{\circ}$ , donc $B \hat{A} O=x \hat{O} A$.
Les deux angles $B \hat{A} O$ et $x \hat{O} A$ sont alternes internes et de même mesure, par conséquent, la droite ( $A B$ ) et la demi-droite $[O X$ ) sont parallèles.
Exercice 9:
On considère deux cercles concentriques (c’est à dire deux cercles de même centre). Soit $O$ ce centre.
$A$ et $B$ sont deux points du cercle $C$ et $M$ et $N$ sont deux points du cercle $C^{\prime}$.
Les points $A, O$ et $M$ sont alignés ainsi que les points $B, O$ et $N$.
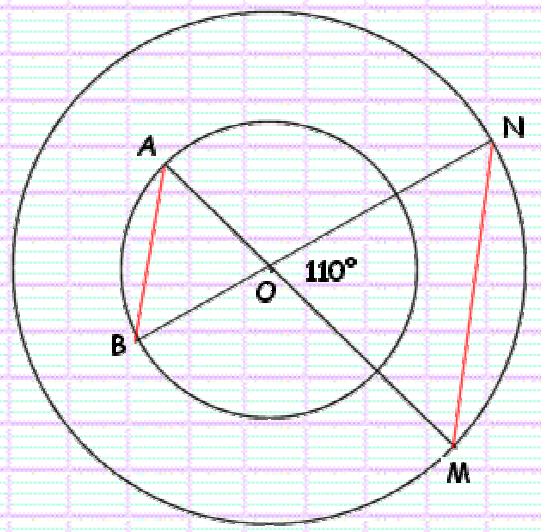
$1)$ Quelle est la nature du triangle $O A B$ ? du triangle $ONM$ ?
$2)$ Calculer les angles du triangle $ONM$.
$3)$ Calculer les angles du triangle $OAB$.
$4)$ Montrer que les droites $(A B)$ et $(MN)$ sont parallèles.
$1)$ Nature des triangles $O A B$ et $O M N$ :
$O A=O B$ (rayons du cercle $C$ )
$\text { Donc le triangle OAB est isocèle en } O$
$O M=O N$ (rayons du cercle $C^{\prime}$ )
$\text { Donc le triangle OMN est isocèle en } O$
$2)$ On a : $MÔN =110^{\circ}$ (voir énoncé)
Comme le triangle $OMN$ est isocèle en $O$ (question a ), les angles à la base ont même mesure.
Nous avons donc :
$ O \hat{M} N=O \hat{N} M=(180-M \hat{N}): 2 $
$ O \hat{M} N=O \hat{N} M=(180-110): 2=70: 2=35^{\circ}$
$3)$ Les angles $AÔB$ et $MÔN$ sont opposés par le sommet.
Donc : $\hat{A O B}=M \hat{O} \mathrm{~N}=110^{\circ}$
De la même façon que précédemment, comme le triangle $O A B$ est isocèle en $O$, nous avons : $\hat{O A B}=O \hat{B A}=(180-A \hat{O}): 2=(180-110): 2=70: 2=35^{\circ}$
$4)$ Les angles $O \hat{A} B$ et $O \hat{M} N$ sont alternes internes et de même mesure ( $O \hat{A} B=O \hat{M} N=35^{\circ}$ ).
Donc : Les droites $(A B)$ et $(M N)$ sont parallèles.
Exercice 10:
On considère la figure ci-contre :
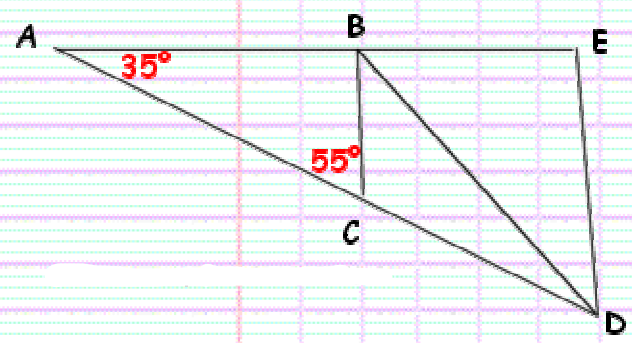
Nous avons: $\hat{B A C}=35^{\circ}$; $\hat{A C B}=55^{\circ}$; $\hat{A B D}=125^{\circ}$ et $\hat{B D E}=35^{\circ}$
• La droite $( A B )$ est-elle perpendiculaire à la droite $(DE)$?
( Aide : Si deux droites sont parallèles, toute droite perpendiculaire à l’une est perpendiculaire à l’autre. )
• Calcul de l’angle $A \hat{B} C$ :
Dans le triangle $A B C$, la somme des angles est égale à $180^{\circ}$.
Donc : $A \hat{B C} C=180-(B \hat{A} C+A \hat{C} B)=180-(35+55)=180-90=90^{\circ}$
• Calcul de l’angle $C \hat{B}$ :
$\hat{C B D}=A \hat{B} D-A \hat{B} C=125-90=35^{\circ}$
• Les droites ( $B C$ ) et ( $E D$ ) sont-elles parallèles?
– Les angles $C \hat{B D}$ et $B \hat{D} E$ sont des angles alternes internes.
– De plus ces deux angles ont même mesure $\left(35^{\circ}\right)$
Donc les droites ( $B C$ ) et $(ED)$ sont parallèles.
• La droite $(A B)$ est-elle perpendiculaire à la droite $(DE)$?
– $(BC) // (ED)$ (question précédente)
– $(B C) \perp(A E)\left(A \hat{B C}=90^{\circ}\right)$
Donc $(ED) \perp (A E)$ (Si deux droites sont parallèles, toute droite perpendiculaire à l’une est perpendiculaire à l’autre.)
La droite $(AE)$ et la droite $(AB)$ sont confondues (même droite)
Donc :$(ED) \perp (A B)$
Exercice 11:
Cette figure à main levée représente un rectangle $ABCD$. De plus, les points $A, B, M$ sont alignés ainsi que les points $D, B, N$.
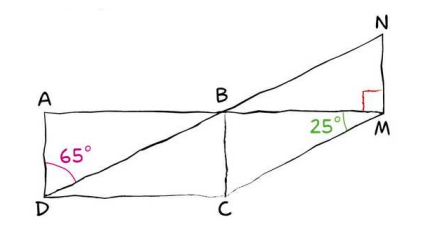
• Quelle est la nature du quadrilatère $ BCMN$ ? Expliquer la réponse
Les droites $(AD)$ et $(BC)$ sont parallèles car $ABCD$ est un rectangle donc les angles alternes-internes $A \hat{B} D$ et $D \hat{B} C $ ont la même mesure.
Donc : $D \hat{B} C = 65°$.
Donc : $A \hat{B} D = 90° −65° = 25°$.
Donc : $N \hat{B} M = A \hat{B} D = 25°$ car ce sont deux angles opposés par le sommet.
Ainsi, les angles alternes-internes $N \hat{B} M$ et $B \hat{M} C$ ont la même mesure.
Les droites $(C M)$ et $(B N)$ sont donc parallèles.
Les droites $(BC)$ et $(M N)$ étant toutes les deux perpendiculaires à la droite $(AM)$, elles sont également parallèles.
Le quadrilatère $B N MC$ a donc ses côtés opposés parallèles, c’est un parallélogramme.
Exercice 12:
$ABCD$ est un trapèze rectangle.
• Déterminer la mesure de l’angle $A \hat{B} C$.
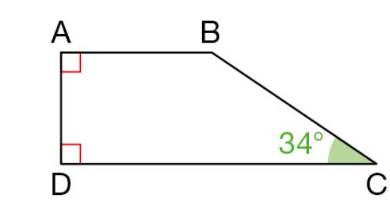
Les droites $(AB)$ et $(DC)$ sont toutes les deux perpendiculaires à la droite $(AD)$.
Or, si deux droites sont perpendiculaires à une même droite alors ces deux droites sont parallèles.
Donc les droites $(AB)$ et $(DC)$ sont parallèles.
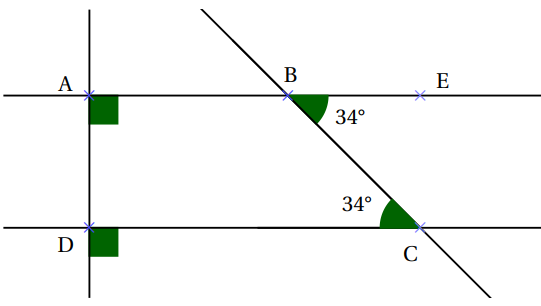
Les angles alternes-internes $B \hat{C} D$ et $C\hat{B} E$ sont donc de même mesure.
Ainsi : $A \hat{B} C = 180° −34° = 146°$.
Exercice 13:
Les pans des toits $[S A]$ et $[T C]$ du collège de Reda sont parallèles ainsi que les pans $[SB] $et $[T A]$.
La pente du toit [S A] est l’angle que $[S A]$ fait avec l’horizontale, c’est-à-dire l’angle $S \hat{A} B$.
De même la pente du toit $[T C]$ est l’angle $T \hat{C} A$ .
Voici un croquis du collège.
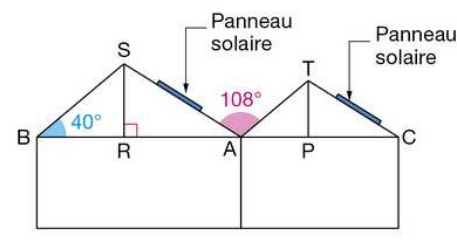
Pour installer des panneaux solaires, l’idéal est d’avoir une pente de toit comprise entre $30°$ et $35°$.
• Peut-on installer des panneaux solaires sur les pans $[S A]$ et $[T C]$ du collège de Reda ?
Les droites $(SB)$ et $(T A)$ sont parallèles donc les angles alternes-internes $S \hat{A} B$ et $T\hat{A}C$ ont la même mesure.
Donc : $T\hat{A}C = 40°$.
Donc : $S\hat{A} B= 180° −108° −40° = 32°$.
Les droites $(S A)$ et $(T C)$ sont également parallèles donc les angles alternes-internes $S\hat{A} B$ et $T\hat{C}A$ ont la même mesure.
Donc : $T \hat{C} A = S \hat{A} B= 32°$.
La pente du toit étant comprise entre $30°$ et $35°$, on pourra installer des panneaux solaires.
Angles formés par deux droites parallèles et une sécante exercices corrigés