Calcul trigonométrique 2-exercices corrigés
📐Exercice 1 :
À l’aide d’un cercle trigonométrique seulement, donner toutes les valeurs possibles de \(x\) vérifiant les conditions données.
❓Questions :
\(\cos x = \frac{1}{2}\) et \(\sin x = -\frac{\sqrt{3}}{2}\) avec : \(x \in ]-\pi, \pi]\)
\(\cos x = \frac{\sqrt{2}}{2}\) et \(\sin x = \frac{\sqrt{2}}{2}\) avec : \(x \in ]-\pi, \pi]\)
\(\cos x = -\frac{\sqrt{3}}{2}\) et \(\sin x = -\frac{1}{2}\) avec : \(x \in [-\pi, 3\pi]\)
\(\cos x = 0\) et \(\sin x = -1\) avec : \(x \in [-2\pi, 3\pi]\)
Équations : \(\cos x = \frac{1}{2}\) et \(\sin x = -\frac{\sqrt{3}}{2}\)
Intervalle : \(x \in ]-\pi, \pi]\)
Raisonnement :
- Sur le cercle trigonométrique, \(\cos x = \frac{1}{2}\) correspond aux angles \(\frac{\pi}{3}\) et \(-\frac{\pi}{3}\).
- La condition \(\sin x = -\frac{\sqrt{3}}{2}\) impose que le sinus soit négatif.
- Sur l’intervalle \(]-\pi, \pi]\), seul l’angle \(-\frac{\pi}{3}\) vérifie les deux conditions simultanément.
Solution : \(x = -\frac{\pi}{3}\)
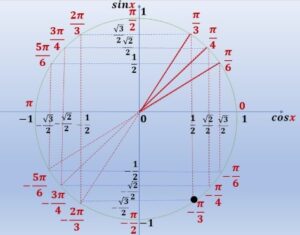
Représentation sur le cercle trigonométrique
Équations : \(\cos x = \frac{\sqrt{2}}{2}\) et \(\sin x = \frac{\sqrt{2}}{2}\)
Intervalle : \(x \in ]-\pi, \pi]\)
Raisonnement :
- Les valeurs \(\cos x = \frac{\sqrt{2}}{2}\) et \(\sin x = \frac{\sqrt{2}}{2}\) correspondent à un angle dont le cosinus et le sinus sont positifs et égaux.
- Cela correspond au premier quadrant du cercle trigonométrique.
- Sur l’intervalle \(]-\pi, \pi]\), l’angle qui vérifie cette condition est \(\frac{\pi}{4}\).
- Note : L’angle \(\frac{\pi}{4}\) a pour cosinus et sinus la même valeur positive \(\frac{\sqrt{2}}{2}\).
Solution : \(x = \frac{\pi}{4}\)
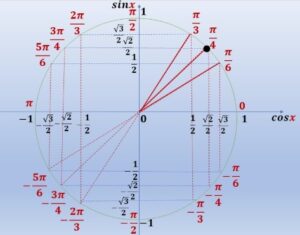
Représentation sur le cercle trigonométrique
Équations : \(\cos x = -\frac{\sqrt{3}}{2}\) et \(\sin x = -\frac{1}{2}\)
Intervalle : \(x \in [-\pi, 3\pi]\)
Raisonnement :
- Un cosinus négatif et un sinus négatif indiquent que l’angle se situe dans le troisième quadrant.
- Les angles de référence sont \(\frac{\pi}{6}\) (pour les valeurs absolues) et \(\frac{5\pi}{6}\) (pour cos négatif).
- Dans le troisième quadrant, l’angle correspondant est \(\pi + \frac{\pi}{6} = \frac{7\pi}{6}\).
- Sur l’intervalle \([-\pi, 3\pi]\), nous devons considérer les angles coïncidants avec cette position sur le cercle :
- \(\frac{7\pi}{6} – 2\pi = -\frac{5\pi}{6}\) (dans l’intervalle)
- \(\frac{7\pi}{6}\) (dans l’intervalle)
- \(\frac{7\pi}{6} + 2\pi = \frac{19\pi}{6}\) (hors intervalle)
Solution : \(x \in \left\{-\frac{5\pi}{6}, \frac{7\pi}{6}\right\}\)
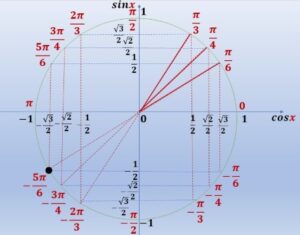
Représentation sur le cercle trigonométrique
Équations : \(\cos x = 0\) et \(\sin x = -1\)
Intervalle : \(x \in [-2\pi, 3\pi]\)
Raisonnement :
- La condition \(\cos x = 0\) correspond aux angles \(\frac{\pi}{2} + k\pi\) où \(k \in \mathbb{Z}\).
- Parmi ceux-ci, \(\sin x = -1\) sélectionne uniquement les angles où le point sur le cercle est en bas : \(-\frac{\pi}{2} + 2k\pi\).
- Sur l’intervalle \([-2\pi, 3\pi]\), nous cherchons les valeurs de \(k\) telles que :
- Pour \(k = 0\) : \(x = -\frac{\pi}{2}\) (dans l’intervalle)
- Pour \(k = 1\) : \(x = -\frac{\pi}{2} + 2\pi = \frac{3\pi}{2}\) (dans l’intervalle)
- Pour \(k = 2\) : \(x = -\frac{\pi}{2} + 4\pi = \frac{7\pi}{2}\) (hors intervalle, supérieur à \(3\pi\))
- Pour \(k = -1\) : \(x = -\frac{\pi}{2} – 2\pi = -\frac{5\pi}{2}\) (hors intervalle, inférieur à \(-2\pi\))
Solution : \(x \in \left\{-\frac{\pi}{2}, \frac{3\pi}{2}\right\}\)
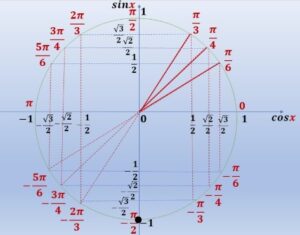
Représentation sur le cercle trigonométrique
📚Exercice 2 : Résolution d’équations trigonométriques
📋Énoncé :
Résoudre dans \(\mathbb{R}\) les équations suivantes :
❓Équations à résoudre :
\(\cos x = \frac{\sqrt{2}}{2}\)
\(\cos x = -\frac{1}{2}\)
\(\cos^2 x = \frac{1}{2}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 3 :
📋Énoncé :
Résoudre dans \(\mathbb{R}\) les équations suivantes :
❓Équations à résoudre :
\(\sin x = \frac{\sqrt{3}}{2}\)
\(\sin x = -\frac{1}{2}\)
\(\sin^2 x = \frac{1}{2}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 4 :
❓Questions :
Résoudre dans \(\mathbb{R}\) l’équation suivante : \(\tan x = \sqrt{3}\).
Résoudre dans \(]-\pi ; \pi]\) l’équation suivante : \(\tan x = \sqrt{3}\).
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 5 :
❓Questions :
Résoudre dans \(\mathbb{R}\) l’équation suivante : \(4 \tan x + 4 = 0\)
Résoudre dans \([-\pi, \pi[\) l’équation suivante : \(2 \cos 2x + \sqrt{3} = 0\)
Résoudre dans \(\left[-\frac{\pi}{2} ; \frac{5\pi}{2}\right]\) l’équation suivante : \(2\sqrt{2} \sin x + 2 = 0\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 6 :
📋Énoncé :
Résoudre dans \(\mathbb{R}\) les équations suivantes :
❓Équations à résoudre :
\(\cos \left(2x + \frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\)
\(\sin(2x) = \cos(3x)\)
\(\tan \left(\frac{\pi}{4} – x\right) = -\sqrt{3}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 7 :
❓Questions :
Résoudre dans \(\mathbb{R}\) l’équation : \(\sin \left(\frac{\pi}{4} – x\right) = \frac{1}{2}\)
En déduire dans \([-\pi ; 2\pi[\) les solutions de l’équation \((E)\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 8 :
📋Énoncé :
Résoudre les équations trigonométriques suivantes.
❓Équations à résoudre :
\(\cos 2x = \cos \left(\frac{8\pi}{2}\right)\) dans \(\mathbb{R}\) puis dans \([\pi ; 5\pi]\)
\(\sin \left(x – \frac{2\pi}{3}\right) = \sin \left(\frac{\pi}{5}\right)\) dans \(\mathbb{R}\) puis dans \([-2\pi ; 2\pi]\)
\(\cos 3x = -\cos x\) dans \(\mathbb{R}\) puis dans \([-2\pi ; \pi]\)
\(\sin \left(2x + \frac{\pi}{4}\right) = -\sin x\) dans \(\mathbb{R}\) puis dans \([4\pi ; 6\pi]\)
\(\sin(3x) = \cos(2x)\) dans \(\mathbb{R}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 9 :
❓Équations à résoudre :
Résoudre dans \(\mathbb{R}\) l’équation : \(\cos 2x = \cos \left(x – \frac{\pi}{3}\right)\)
Résoudre dans \([0 ; \pi]\) l’équation : \(\sin \left(2x – \frac{\pi}{3}\right) = \sin \left(\frac{\pi}{4} – x\right)\)
Résoudre dans \(\left]-\frac{\pi}{2} ; \frac{\pi}{2}\right[\) l’équation : \(\tan \left(2x – \frac{\pi}{5}\right) = 1\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 10 :
Représenter sur un cercle trigonométrique l’ensemble des points du cercle associés aux réels \(x\) vérifiant les conditions suivantes :
❓Questions :
\(0 \leq \cos(x) \leq 1\)
\(\cos(x) \in \left[\frac{1}{2}; 1\right]\)
\(-1 < \sin(x) < 0\)
\(-\frac{1}{2} \leq \sin(x) \leq 1\)
\(\sin(x) \in \left[-\frac{\sqrt{2}}{2}; 0\right[\)
\(\cos(x) \in \left[-\frac{1}{2}; \frac{\sqrt{3}}{2}\right]\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 11 :
Résoudre les inéquations trigonométriques suivantes dans les intervalles donnés.
Utilisez le cercle trigonométrique pour déterminer les solutions.
❓Questions :
Résoudre dans \( [0, 2\pi[ \) l’inéquation suivante : \(\sin x \geq \frac{1}{2}\)
Résoudre dans \( ]-\pi, \pi] \) l’inéquation suivante : \(\sin x \leq -\frac{1}{2}\)
Résoudre dans \( ]-\pi, \pi] \) l’inéquation suivante : \(\cos x \geq \frac{\sqrt{2}}{2}\)
Résoudre dans \( ]-\frac{\pi}{2}, \pi] \) l’inéquation suivante : \(\cos x \leq \frac{1}{2}\)
Résoudre dans \( [0, 2\pi] \) l’inéquation suivante : \(\cos x < \frac{\sqrt{3}}{2}\)
Résoudre dans \( [0, 2\pi] \) l’inéquation suivante : \(\tan x – 1 \geq 0\)
Résoudre dans \( [0, 2\pi] \) l’inéquation suivante : \(\tan x > -1\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 12 :
Résoudre les équations et inéquations trigonométriques suivantes.
❓Questions :
a) Équation du second degré en \(\sin x\)
Résoudre dans \(\mathbb{R}\) l’équation suivante : \(2 \sin^{2} x – 9 \sin x – 5 = 0\)
et en déduire les solutions dans \([0 ; 2\pi]\)
b) Inéquation associée
Résoudre dans \([0 ; 2\pi]\) l’inéquation suivante : \(2 \sin^{2} x – 9 \sin x – 5 \leq 0\)
Résoudre dans \([0 ; \pi]\) l’inéquation suivante : \((2 \cos x – 1)(\tan x + 1) \geq 0\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 13 :
On considère l’expression trigonométrique suivante :
\(E(x) = \sin\left(2x + \frac{\pi}{4}\right) – \cos\left(2x + \frac{3\pi}{4}\right)\) avec \(x \in \mathbb{R}\)
❓Questions :
Calculer : \(E(0)\) et \(E(\pi)\)
Montrer que : \(E(x) = 2 \sin\left(2x + \frac{\pi}{4}\right)\)
Résoudre dans \(\mathbb{R}\) l’équation : \((E) \quad E(x) = -\sqrt{2}\)
Résoudre dans \([0 ; \pi]\) l’inéquation : \((I) \quad E(x) \leq -\sqrt{2}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 14 :
À partir du triangle de la figure suivante, déterminez les éléments demandés.
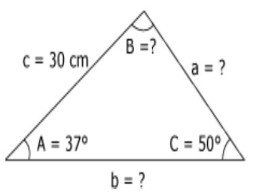
❓Questions :
Trouver la valeur du côté \(a\) (côté opposé à l’angle A)
Trouver la mesure de l’angle \(B\)
Trouver la valeur du côté \(b\) (côté adjacent à l’angle A)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 15 :
Soit \(ABC\) un triangle tel que :
\(BC = \sqrt{3}\)
\(\widehat{BCA} = \frac{\pi}{4}\)
\(\widehat{BAC} = \frac{\pi}{3}\)
❓Questions :
Calculer : \(AB\)
a) Vérifier que : \(\widehat{ABC} = \frac{5\pi}{12}\)
b) Calculer : \(\sin \frac{5\pi}{12}\) sachant que : \(AC = \frac{\sqrt{6} + \sqrt{2}}{2}\)
Et en déduire la valeur de \(\cos \frac{\pi}{12}\).
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 16 :
Calculer le périmètre et la surface d’un parallélogramme \(ABCD\) tel que :
\(AB = 4\ \text{cm}\)
\(BC = 3\ \text{cm}\)
\(\widehat{ABC} = \frac{2\pi}{3}\)
❓Calculs à effectuer :
Calculer le périmètre du parallélogramme \(ABCD\)
Calculer la surface (aire) du parallélogramme \(ABCD\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
📐Exercice 17 :
Soit \(ABC\) un triangle tel que :
\(BC = \sqrt{2}\)
\(AC = \frac{\sqrt{2}}{3}\)
\(\widehat{BAC} = \frac{3\pi}{4}\)
❓Questions :
Vérifier que : \(\sin \frac{3\pi}{4} = \frac{\sqrt{2}}{2}\)
Calculer : \(\sin \widehat{ABC}\) et en déduire la valeur de \(\cos \widehat{ABC}\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
Calcul trigonométrique 2
