Devoirs Corrigés Maths N°1 S1 1AC
Modèle N°1
Exercice 1:(8 pts)
1) Calculer les expressions suivantes: $(1 \times 4=4$ pts)
$A=4,7-1,7+0,3$
$B=36 \div 6 \times 3$
C $=3,7+1,3 \times 2$
$D=1,2+2,5 \times(1,2+0,8)$
2) Développer cette expression : (1pt)
$E=3 \times(x-2)$
3) Factoriser cette expression : (1pt)
$F=9 \times a+9 \times x$
4) Calculer par deux méthodes différentes : $(1 \times 2=2 $ pts)
$A=100 \times(0,8+2,11)$
$B=2,23 \times 217-2,23 \times 117$
Exercice 2:(5 pts)
1) Recopier et compéter par le nombre qui convient : $(1,5 \times 2=3 $ pts)
$\frac{5}{3}=\frac{5 \times \cdots}{3 \times \cdots}=\frac{\cdots}{12}$
$\frac{24}{55}=\frac{24 \div \cdots}{\ldots \div \cdots}=\frac{4}{\ldots}$
2) Comparer ces fractions : (2 pts)
$\frac{5}{4} \ldots \frac{9}{4} \quad ; \quad \frac{5}{3} \ldots \frac{7}{12} \quad ; \quad \frac{6}{5} \ldots 1 \quad ; ; \quad \frac{7}{6} \ldots 1$
Exercice 3:(6 pts)
Calculer et simplifier si possible ces expressions : $(1 \times 6=6$ pts)
1) $\frac{4}{5}+\frac{11}{5}=\cdots$
2) $\frac{13}{7}-\frac{6}{7}=\cdots$
3) $\frac{6}{5}-\frac{7}{15}=\cdots$
4) $\frac{5}{3} \times \frac{7}{2}=\cdots$
5) $\frac{4}{35} \times \frac{5}{8}=\cdots$
6) $\frac{5}{6} \div \frac{7}{3}=\cdots$
Exercice 4:(1 pt)
Nabil procède 170 DH , il a acheté une trousse à 9 DH et cinq cahiers de 23 DH chacun.
1) Ecrire les calculs qui donnent le prix à payer par Nabil.
2) Déterminer le montant qui reste à Nabil
Modèle N°2
Exercice 1:(7 pts)
1) Calculer les expressions suivantes: $(1 \times 5=5$ pts)
$A=25+3 \times 6 \quad $
$B=24,9+4,8-2,1 \quad$
$C=10 \times 7 \div 5 \quad$
$D=120 \div 3-6 \times 6+5 \quad$
$ E=[(10-3) \div 2+8 \div 5] \times 4$
2) Calculer $F$ de deux manières différentes : $(1 \times 2=2$ pts)
$F=7 \times 13,3+7 \times 6,7 $
$G=7 \times 13,3+7 \times 6,7$
Exercice 2:(10 pts)
1) Comparer en justifiant votre réponse : $(0,5 \times 5=2,5 $ pts)
$\frac{3}{5}$ et $\frac{6}{5}\quad$ ; $\quad1$ et $\frac{23}{66} \quad;\quad 1$ et $\frac{66}{13} \quad ; \quad\frac{66}{13}$ et $\frac{23}{66}\quad ;\quad \frac{5}{16}$ et $\frac{1}{4}$
2) Calculer:$(1\times 6=6 $ pts)
$A=\frac{5}{7}+\frac{1}{7}$
$ B=\frac{10}{4,3}-\frac{9,9}{4,3}$
$ C=\frac{5}{12}+\frac{7}{6}$
$ D=\frac{15}{3}-\frac{20}{6}$
$ E=\frac{15}{3} \times \frac{20}{6}$
$ F=1.5 \times \frac{7}{2}$
3) Simplifier les fractions suivantes: $(0,5 \times 3=1,5 $ pts)
$\frac{8}{10}=\ldots$
$\frac{50}{75}=\ldots$
$\frac{21}{30} \times \frac{15}{7}=\ldots$
Exercice 3:$(0,5 \times 6=3 $ pts)
1) Trace trois points $A, B$ et $C$ non alignés.
2) Trace la droite (d1) perpendiculaire à (BC) qui passe par B.
3) Trace la droite (d2) perpendiculaire à (BC) qui passe par A.
4) Que peux-tu dire des droits (d1) et (d2)?
5) Trace la droite (d 3) parallèle à ( BC ) qui passe par A.
6) Explique comment tu as effectué ce dernier tracé.
Modèle N°3
Exercice 1:(7 pts)
1) Calculer les expressions suivantes: $(1 \times 5=5$ pts)
$A=25+3 \times 6$
$B=24,9+4,8-2,1$
$C=10 \times 7 \div 5$
$D=120 \div 3-6 \times 6+5$
$ E=[(10-3) \div 2+8 \div 5] \times 4$
2) Calculer par deux méthodes différentes : $(1 \times 2=2 $ pts)
$F=7 \times 13,3+7 \times 6,7$
$G=7 \times 13,3+7 \times 6,7$
Exercice 2:(10,5 pts)
1) Comparer en justifiant votre réponse : $(0,5 \times 5=2,5 $ pts)
$\frac{3}{5} \text { et } \frac{6}{5}$
$1 \text { et } \frac{23}{66}$
$1 \text { et } \frac{66}{13}$
$\frac{66}{13} \text { et } \frac{23}{66}$
$\frac{5}{16} \text { et } \frac{1}{4}$
2) Calculer : $(1 \times 6=6$ pts)
$A=\frac{5}{7}+\frac{1}{7}$
$B=\frac{10}{4,3}-\frac{9,9}{4,3}$
$C=\frac{5}{12}+\frac{7}{6}$
$D=\frac{15}{3}-\frac{20}{6}$
$E=\frac{5}{9} \times \frac{4}{3}$
$F=1,5 \times \frac{7}{2}$
3) Simplifier les fractions suivantes :$(1 \times 3=3$ pts)
$\frac{8}{10}=$
$\frac{50}{75}=$
$\frac{21×15}{30×7}=$
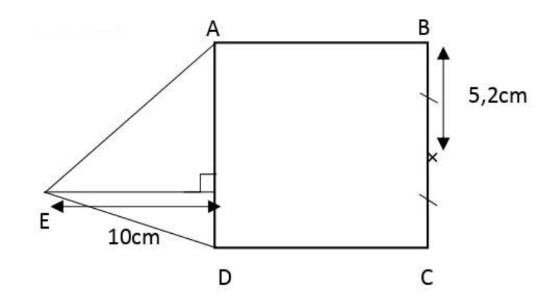
Exercice 3:(1,5 pts)
1) Calculer l’aire de la figure ci-contre :
Modèle N°4
Exercice 1 (5pts)
1. Calculer les expressions suivantes en écrivant les étapes intermédiaires (1pt × 2) :
A = 12,75 – 8,85 + 2,7
B = 120 – [100 × 2 – 2(450 ÷ 9)]
2. Écrire sous forme d’une différence, puis effectuer les calculs (1pt) :
C = 120 × (0,1 – 0,01)
3. Écrire sous forme d’un produit, puis effectuer les calculs (1pt) :
D = 129 × 6,109 + 129 × 3,891
4. Simplifier l’expression E telle que x et y désignent deux nombres décimaux (1pt) :
E = 5x + 6y – x – 4y
Exercice 2 (7pts)
1. Écrire sous forme d’une fraction irréductible les nombres suivants (0,75pt × 2) :
\(A = \frac{140}{60} \quad ; \quad B = 0,125\)
2. Comparer (1pt) :
\(\frac{23}{10} \quad et \quad \frac{2018}{2019}\)
3. Calculer et simplifier (1,5pt × 2) :
\(C = \frac{29}{12} – \left( \frac{7}{4} + \frac{1}{3} \right)\)
\(D = \frac{9}{5} \times \frac{25}{81} + \frac{28}{27} \times \frac{3}{7}\)
4. Problème (1,5pt) :
Sami fait trois parties de billes au cours desquelles il perd successivement le \(\frac{1}{4}\), puis les \(\frac{2}{5}\), puis le \(\frac{1}{3}\) des billes qu’il possédait en entrant dans le jeu. Il se retire alors avec une seule bille.
Combien avait-il de billes avant de jouer ?
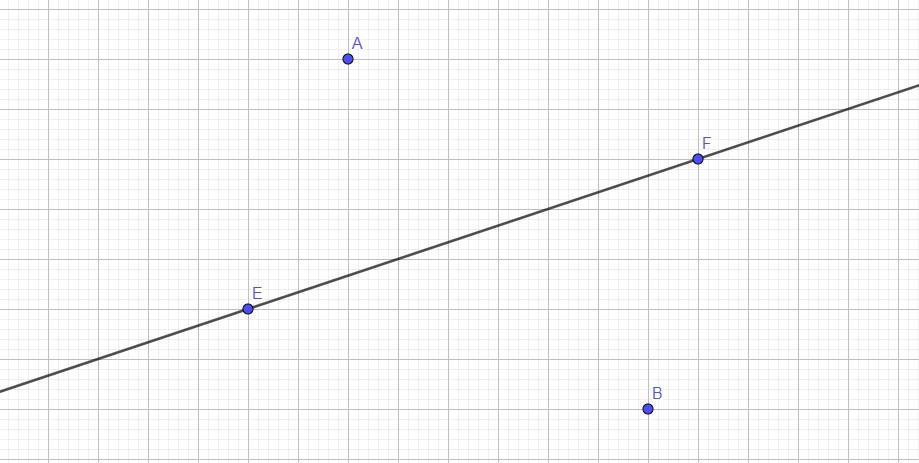
Exercice 3 (8pts)
Sur la figure ci-dessus construire :
1. La droite (D) passant par A et parallèle à (A). (1pt)
2. C le point d’intersection des deux droites (AB) et (EF). (1pt)
3. Le point K tel que : K ∈ [EF] et K ∉ [EF]. (1pt)
4. Le point H le projeté orthogonal de B sur (D). (1pt)
5. Le point L le milieu du segment [EF]. (1pt)
6. Montrer que les trois points L, G et K sont alignés. (1pt)
7. Montrer que (EF) est perpendiculaire à (BH). (1pt)
8. Supposons que LF = 3cm et FK = 2cm, calculer la distance EK. (1pt)
Devoirs Corrigés Maths N°1 S1 1AC
