Devoirs Corrigés Maths N°1 S1 2AC
Devoir Surveillé N°1-1
Exercice 1 : (14 pts)
14 pts1) Calculer : (1 × 6 = 6 pts)
\(-12 + (-9)\)
\(+21 \div (-7)\)
\((-19) + (+7)\)
\((-5) \times (-9)\)
\(-7 – 31\)
\(-7 + 7 \times (-3)\)
2) Donner le signe des nombres suivants : (1 pt)
\(\frac{-39}{+52} \quad ; \quad \frac{-93 \times 5 \times (-4)}{14 \times (-7) \times (-3)}\)
3) Parmi les nombres rationnels suivants, entourer en vert les nombres décimaux relatifs. (1 pt)
\(\frac{-17}{4} \quad ; \quad \frac{49}{-3} \quad ; \quad \frac{-67}{-11} \quad ; \quad \frac{-36}{-5}\)
4) Compléter les égalités suivantes. (1 pt)
\(\frac{4}{-5} = \frac{-28}{\cdots} \quad ; \quad \frac{-28}{-36} = \frac{\cdots}{9}\)
5) Entourer en bleu les fractions irréductibles. (1 pt)
\(\frac{-12}{13} \quad ; \quad \frac{69}{20} \quad ; \quad \frac{31}{-5} \quad ; \quad -\frac{11}{3}\)
6) Simplifier chaque fraction au maximum. (1 pt)
\(\frac{-45}{25} = \cdots \quad ; \quad \frac{132}{-96} = \cdots\)
7) Les fractions \(\frac{-8}{6}\) et \(\frac{12}{-9}\) sont-elles égales ? Justifier. (1 pt)
8) Comparer les fractions suivantes. (1 × 2 = 2 pts)
\(\frac{-13}{27} \quad \cdots \quad \frac{-21}{27} \quad ; \quad \frac{-29}{18} \quad \cdots \quad \frac{11}{-6}\)
Exercice 2 : (6 pts)
6 pts
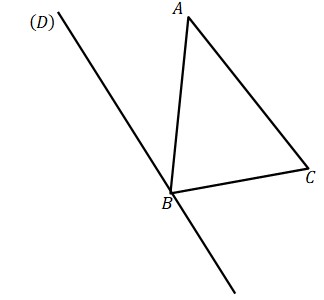
Dans la figure ci-dessous on a :
\(AC = 7 \quad ; \quad \widehat{ACB} = 65^{\circ} \quad \text{et} \quad \widehat{ABC} = 50^{\circ}\)
1) Construire \(A’\) et \(C’\) les symétriques respectifs de \(A\) et \(C\) par rapport à \((D)\). (2 pts)
2) Quel est le symétrique de \(B\) par rapport à \((D)\) ? (0,75 pt)
3) Montrer que \(A’C’ = 7\). (0,75 pt)
4) Quelle est la mesure de l’angle \(\widehat{A’C’B}\) ? Justifier. (0,75 pt)
5) Soit \(E\) un point appartient à \([AB]\).
a) Construire \(E’\) le symétrique de \(E\) par rapport à \((D)\). (0,75 pt)
b) Montrer que les points \(A’\), \(B\) et \(E’\) sont alignés. (1 pt)
Corrigé du Devoir Surveillé N°1-1
Exercice 1 : (14 pts)
14 pts
1) Calculer : (1 × 6 = 6 pts)
\(-12 + (-9)\)
\(-12 + (-9) = \color{#27ae60}{-21}\)
✓ Addition de deux nombres négatifs.
\(+21 \div (-7)\)
\(21 \div (-7) = \color{#27ae60}{-3}\)
✓ Division d’un nombre positif par un nombre négatif.
\((-19) + (+7)\)
\((-19) + (+7) = \color{#27ae60}{-12}\)
✓ Addition de nombres de signes contraires.
\((-5) \times (-9)\)
\((-5) \times (-9) = \color{#27ae60}{45}\)
✓ Produit de deux nombres négatifs.
\(-7 – 31\)
\(-7 – 31 = \color{#27ae60}{-38}\)
✓ Soustraction de deux nombres.
\(-7 + 7 \times (-3)\)
\(-7 + 7 \times (-3) = -7 + (-21) = \color{#27ae60}{-28}\)
✓ La multiplication est prioritaire : \(7 \times (-3) = -21\).
2) Donner le signe des nombres suivants : (1 pt)
\(\frac{-39}{+52}\)
\(\frac{-39}{+52}\) est de signe négatif (car \(- \div + = -\))
\(\frac{-93 \times 5 \times (-4)}{14 \times (-7) \times (-3)}\)
Numérateur : \((-93) \times 5 \times (-4)\) → produit de deux signes négatifs = positif
Dénominateur : \(14 \times (-7) \times (-3)\) → produit de deux signes négatifs = positif
Donc la fraction est de signe positif.
3) Parmi les nombres rationnels suivants, entourer en vert les nombres décimaux relatifs. (1 pt)
\(\frac{-17}{4} \quad ; \quad \frac{49}{-3} \quad ; \quad \frac{-67}{-11} \quad ; \quad \frac{-36}{-5}\)
\(\frac{-17}{4} = -4,25\) → décimal relatif
\(\frac{49}{-3} \approx -16,33\) → non décimal (périodique)
\(\frac{-67}{-11} \approx 6,09\) → non décimal (périodique)
\(\frac{-36}{-5} = 7,2\) → décimal relatif
✓ Un nombre décimal relatif a une écriture décimale finie.
4) Compléter les égalités suivantes. (1 pt)
\(\frac{4}{-5} = \frac{-28}{\cdots} \quad ; \quad \frac{-28}{-36} = \frac{\cdots}{9}\)
\(\frac{4}{-5} = \frac{4 \times (-7)}{-5 \times (-7)} = \frac{-28}{35}\) → le nombre manquant est 35
\(\frac{-28}{-36} = \frac{-28 \div (-4)}{-36 \div (-4)} = \frac{7}{9}\) → le nombre manquant est 7
5) Entourer en bleu les fractions irréductibles. (1 pt)
\(\frac{-12}{13} \quad ; \quad \frac{69}{20} \quad ; \quad \frac{31}{-5} \quad ; \quad -\frac{11}{3}\)
\(\frac{-12}{13}\) → PGCD\((12,13)=1\) → irréductible
\(\frac{69}{20}\) → PGCD\((69,20)=1\) → irréductible
\(\frac{31}{-5}\) → PGCD\((31,5)=1\) → irréductible
\(-\frac{11}{3}\) → PGCD\((11,3)=1\) → irréductible
✓ PGCD : Plus grand commun diviseur.
6) Simplifier chaque fraction au maximum. (1 pt)
\(\frac{-45}{25}\)
\(\frac{-45}{25} = \frac{-45 \div 5}{25 \div 5} = \color{#27ae60}{-\frac{9}{5}}\)
\(\frac{132}{-96}\)
\(\frac{132}{-96} = \frac{132 \div 12}{-96 \div 12} = \frac{11}{-8} = \color{#27ae60}{-\frac{11}{8}}\)
7) Les fractions \(\frac{-8}{6}\) et \(\frac{12}{-9}\) sont-elles égales ? Justifier. (1 pt)
Réponse :
\(\frac{-8}{6} = \frac{-8 \div 2}{6 \div 2} = \frac{-4}{3}\)
\(\frac{12}{-9} = \frac{12 \div 3}{-9 \div 3} = \frac{4}{-3} = -\frac{4}{3}\)
\(\frac{-4}{3} = -\frac{4}{3}\)
Donc \(\frac{-8}{6} = \frac{12}{-9}\)
8) Comparer les fractions suivantes. (1 × 2 = 2 pts)
\(\frac{-13}{27} \quad \cdots \quad \frac{-21}{27}\)
Même dénominateur \((27)\) → on compare les numérateurs : \(-13 > -21\)
\(\frac{-13}{27} > \frac{-21}{27}\)
\(\frac{-29}{18} \quad \cdots \quad \frac{11}{-6}\)
\(\frac{11}{-6} = -\frac{11}{6}\)
On met au même dénominateur \((18)\) :
\(-\frac{11}{6} = -\frac{11 \times 3}{6 \times 3} = -\frac{33}{18}\)
Comparaison : \(-29 > -33\)
\(\frac{-29}{18} > \frac{11}{-6}\)
✅ Réponses finales :
1) \(-21\) | \(-3\) | \(-12\) | \(45\) | \(-38\) | \(-28\)
2) Négatif, Positif | 3) \(\frac{-17}{4}\) et \(\frac{-36}{-5}\)
4) \(35\) et \(7\) | 5) Toutes les fractions sont irréductibles
6) \(-\frac{9}{5}\) et \(-\frac{11}{8}\) | 7) \(\frac{-8}{6} = \frac{12}{-9}\)
8) \(\frac{-13}{27} > \frac{-21}{27}\) et \(\frac{-29}{18} > \frac{11}{-6}\)
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Devoir Surveillé N°1-2
Exercice 1 : (4 pts)
4 pts1) Calculer les expressions suivantes : (1 × 2 = 2 pts)
\(A = 11 – 12 \times (-3) + 16 \div (-4)\)
\(B = 8 + (4 – 3 + 9 \div (-3)) \times 5\)
2) \(x\) et \(y\) sont deux nombres décimaux relatifs, supprimer les crochets et les parenthèses puis simplifier : (1 × 2 = 2 pts)
\(C = -3x + [(2x + 4y – 7) – (y + x)]\)
\(D = -(4x + 5y – 9) – [3 – (3x + 3y) – 8x]\)
Exercice 2 : (5 pts)
5 pts1) Compléter par le nombre manquant : (0,5 × 4 = 2 pts)
\(\frac{-6}{12} = \frac{12}{\cdots} = \frac{\cdots}{-36} = \frac{-1}{\cdots} = \frac{\cdots}{60}\)
2) Rendre les nombres rationnels suivants irréductibles : (1 × 3 = 3 pts)
\(E = \frac{75}{-15} \quad ; \quad F = \frac{49 \times (-81)}{9 \times 7}\)
\(G = \frac{4 \times (-5) \times 27 \times (-22)}{-20 \times 9 \times (-11) \times (-21)}\)
3) Montrer que les nombres rationnels : (1 pt)
\(-\frac{112}{5} \quad \text{et} \quad \frac{336}{-15} \quad \text{sont égaux.}\)
Exercice 3 : (7 pts)
7 pts1) Calculer et simplifier : (1 × 6 = 6 pts)
\(A = \frac{-17}{17} + \frac{6}{17} \quad ; \quad B = \frac{-3}{7} – \frac{4}{28}\)
\(C = \frac{-7}{8} – \left(-\frac{7}{8}\right) \quad ; \quad D = 2 + \frac{3}{4} + \frac{7}{2}\)
\(E = 0,5 – \frac{4}{3} + \frac{-1}{2} \quad ; \quad F = \frac{5}{3} + \frac{-2}{6} – \frac{1}{12} – \frac{-5}{12}\)
2) Supprimer les parenthèses et les crochets puis calculer et simplifier l’expression : (1 pt)
\(R = \left(\frac{3}{4} – \frac{1}{3}\right) – \left[3 – \left(\frac{1}{3} – \frac{3}{2}\right)\right] – 5\)
Exercice 4 : (1 pt)
1 ptRanger les nombres rationnels dans l’ordre décroissant : (justifier ta réponse)
\(1,5 \quad ; \quad \frac{-2}{5} \quad ; \quad \frac{3}{10} \quad ; \quad \frac{7}{2}\)
Exercice 5 : (1 pt)
1 ptDéterminer la valeur de \(x\) dans chaque cas :
\(\frac{3}{4} + x = \frac{-1}{2} \quad ; \quad \frac{3+x}{5+x} = \frac{1}{2}\)
Exercice 6 : (1 pt)
1 ptQuatre personnes Ahmed, Said, Rachid et Khalid doivent partager le montant d’une facture de 1200 Dh de la façon suivante :
La part de Ahmed est égale à \(\frac{3}{20}\) de la facture.
La part de Said est égale à 2 fois la part de Ahmed.
La part de Rachid est égale au \(\frac{3}{4}\) de la part de Said.
La part de Khalid est le reste. Calculer la part de chacun.
Exercice 7 : (1 pt)
1 ptSoit \(n\) un nombre entier naturel non nul vérifier que :
\(\frac{1}{n} + \frac{1}{2n} + \frac{2}{4n} = \frac{2}{n}\)
Écrire le nombre rationnel \(\frac{2}{11}\) sous forme d’une somme de trois nombres rationnels.
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Devoir Surveillé N°1-3
Mathématiques
2ème Année Collège
1 heure
20 points
Exercice 1 : (5 pts)
5 pts
1) Calculer les expressions suivantes : (1 × 2 = 2 pts)
\(A = -17 + 13 – 5,8 – 11 + 4,9\)
\(B = 6 \times 3 – 42 \div 7 – (2 + 4 \times 3)\)
2) Calculer les expressions suivantes : (1 × 3 = 3 pts)
\(C = -7 – 11 \quad ; \quad D = -12 + 21\)
\(E = 4,5 – 9,5 \quad ; \quad F = -12 \times 7\)
\(G = -9 \times (-3,7) \quad ; \quad H = (-21,7) \div 7\)
Exercice 2 : (4,5 pts)
4,5 pts
1) Compléter par les nombres manquants : (1 pt)
\(-\frac{\cdots}{77} = \frac{-6}{\cdots} = \frac{3}{-7} = \frac{\cdots}{21} = \frac{12}{\cdots}\)
2) Simplifier l’écriture des nombres rationnels suivants : (1 × 2 = 2 pts)
\(I = \frac{-45}{135} \quad ; \quad J = \frac{-33 \times 24 \times (-4)}{12 \times (-8) \times (-44)}\)
3) Déterminer le nombre rationnel \(x\) qui vérifie : (1,5 pt)
\(\frac{2x + 4}{3x – 2} = \frac{3}{7}\)
Exercice 3 : (4 pts)
4 pts
1) Comparer les deux nombres rationnels dans les cas suivants (\(=\) ou \(\neq\)) : (1 × 2 = 2 pts)
\(\frac{2}{-3} \quad \text{et} \quad \frac{-8}{12} \quad ; \quad \frac{-5}{3} \quad \text{et} \quad \frac{7}{-5}\)
2) Comparer les deux nombres rationnels dans les cas suivants (\(\succ\) ou \(\prec\)) : (1 × 2 = 2 pts)
\(\frac{3}{7} \quad \text{et} \quad \frac{5}{8} \quad ; \quad \frac{-9}{11} \quad \text{et} \quad \frac{-11}{12}\)
Exercice 4 : (5,25 pts)
5,25 pts
Calculer et simplifier : (0,75 × 7 = 5,25 pts)
\(K = \frac{-3}{5} + \left(\frac{7}{-5}\right) \quad ; \quad L = \left(\frac{-6}{-5}\right) + \frac{-8}{3}\)
\(M = \left(\frac{12}{-7}\right) – \left(\frac{-8}{2}\right) \quad ; \quad N = \frac{9}{2} + \frac{10}{3} + \frac{-5}{6}\)
\(O = \left(-\frac{3}{25}\right) \times \left(-\frac{5}{9}\right) \quad ; \quad P = \frac{\frac{-4}{7}}{\frac{-16}{-49}}\)
\(Q = \frac{7}{9} – \frac{7}{9} \times \left(\frac{-3}{2}\right)\)
Exercice 5 : (1,25 pt)
1,25 pt
Supprimer les parenthèses et les crochets puis simplifier les expressions suivantes :
\(R = \frac{4}{3} – \left(\frac{7}{8} + \frac{2}{5}\right) – \left[\frac{16}{12} – \left(\frac{21}{24} – \frac{7}{10}\right)\right]\)
Exercice 6 : (Bonus)
Bonus
\(a\), \(b\) et \(c\) trois nombres rationnels non nuls tels que :
\(2a – 4b + 3c = \frac{31}{12} \quad \text{et} \quad abc = \frac{-5}{72}\)
Calculer et simplifier :
\(S = \frac{1}{12ab} + \frac{1}{18bc} – \frac{1}{9ac}\)
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Devoir Surveillé N°1-4
Mathématiques
2ème Année Collège
1 heure
20 points
Exercice 1 : (4 pts)
4 pts
1) Calculer les expressions suivantes : ( 1 pt)
\(A = -18 + 15 – 6,2 – 13 + 5,1\)
\(B = 19 \times 4 – 48 \div 6 – (3 + 5 \times 2)\)
2) Calculer les expressions suivantes : ( 3 pts)
\(C = -9 – 14 \quad ; \quad D = -15 + 24\)
\(E = 5,2 – 8,7 \quad ; \quad F = -14 \times 6\)
\(G = -8 \times (-4,2) \quad ; \quad H = (-18,6) \div 6\)
Exercice 2 : (3 pts)
3 pts
1) Compléter par les nombres manquants : ( 2 pts)
\(\frac{-8}{\cdots} = \frac{4}{-5} = \frac{\cdots}{20} = \frac{-24}{\cdots}\)
2) Simplifier l’écriture des nombres rationnels suivants : ( 1 pt)
\(I = \frac{-42}{126} \quad ; \quad J = \frac{-28 \times 18 \times (-3)}{9 \times (-6) \times 35}\)
Exercice 3 : (3,5 pts)
3,5 pts
1) Comparer les deux nombres rationnels dans les cas suivants (\(=\) ou \(\neq\)) : ( 2 pts)
\(\frac{3}{-4} \quad \text{et} \quad \frac{-9}{12} \quad ; \quad \frac{-4}{5} \quad \text{et} \quad \frac{6}{-7}\)
2) Déterminer le nombre rationnel \(x\) qui vérifie : ( 1,5 pt)
\(\frac{3x + 5}{4x – 3} = \frac{2}{5}\)
Exercice 4 : (2,5 pt)
2,5 pt
Calculer et simplifier :
\(K = \frac{-3}{4} + \left(\frac{5}{4}\right) \quad ; \quad L = \left(\frac{-5}{-7}\right) + \frac{-6}{2}\)
\(M = \frac{10}{6} – \left(\frac{-6}{3}\right) \quad ; \quad N = \frac{7}{3} + \frac{8}{4} + \frac{-4}{5}\)
Exercice 5 : (1,5 pt)
1,5 pt
Supprimer les parenthèses et les crochets puis simplifier l’expression suivante :
\(R = \frac{5}{4} – \left(\frac{6}{7} + \frac{3}{4}\right) – \left[\frac{15}{10} – \left(\frac{18}{21} – \frac{5}{8}\right)\right]\)
Exercice 6 : (5,5 pts)
5,5 pts
\(ABC\) est un triangle tel que :
\(AB = 5\) cm \(\quad ; \quad \widehat{ABC} = 60^{\circ} \quad \text{et} \quad \widehat{CAB} = 40^{\circ}\)
\(M\) est le milieu du segment \([BC]\).
\(B’\) est le symétrique de \(B\) par rapport à la droite \((AM)\).
\(C’\) est le symétrique de \(C\) par rapport à la droite \((AM)\).
1) Faire une figure convenable. ( 1,5 pt)
2) Déterminer le symétrique de la droite \((AB)\) par rapport à la droite \((AM)\). ( 1 pt)
3) Montrer que les points \(B’\), \(M\) et \(C’\) sont alignés. ( 1,5 pt)
4) Montrer que \(\widehat{AB’C’} = 60^\circ\) (justifier). ( 1,5 pt)
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Devoirs Corrigés Maths N°1 S1 2AC