Devoirs Corrigés Maths N°1 S2 1AC
EXERCICE 1
(9 pts)
1) Développer et simplifier les expressions suivantes : (6×1 = 6 pts)
\(2(x+3) =\)
\(-3(x-\frac{1}{2}) =\)
\(2x(x-2) =\)
\((x+2)(x+1) =\)
\((x+1)(x-2) =\)
\((x+2)^2 =\)
2) Factoriser : (4×1 = 4 pts)
A = \(3x + 9y\)
B = \(5x – 15\)
C = \(ab – 3b\)
D = \(5(x-1) – 3(x-1)\)
EXERCICE 2
(9 pts)
1) Résoudre les équations suivantes : (4×1 = 4 pts)
\(3x = 6\)
\(x – 9 = 11\)
\(x + 1,5 = -3\)
\(3x – 8 = x + 12\)
2) Problème : (2 pts)
Aicha et Ahmed pèsent ensemble 137 kg. Ahmed a 11 kg de plus qu’Aicha. Quel est le poids d’Aicha ? et celui d’Ahmed ?
EXERCICE 3
(4 pts)
\([AB]\) un segment de longueur 5 cm et \(O\) un point à l’extérieur de ce segment.
\(M\) le symétrique du point \(A\) par rapport à \(O\).
\(N\) le symétrique du point \(B\) par rapport à \(O\).
1) Construire la figure.
2) Déterminer le symétrique du segment \([AB]\) par rapport à \(O\).
3) Montrer que \(MN = 5\) cm.
4) Montrer que \((AB) \parallel (MN)\).
🔒 Abonnez-vous pour accéder à la correction détaillée .
EXERCICE 1
(6 pts)
1) Développer et simplifier les expressions suivantes : (0,75 pt × 2)
A = \(2(4-5x)\)
B = \((x-1)(3x+7)\)
2) Développer à l’aide d’une identité remarquable : (0,5 pt + 0,75 pt)
C = \((x+3)^{2}\)
D = \((2x-7)(2x+7)\)
3) Factoriser à l’aide d’un facteur commun : (0,75×2 = 1,5 pt)
E = \(8x^{4}-16x^{2}\)
F = \((5x-7)(2x+1)+10x-14\)
4) Factoriser à l’aide d’une identité remarquable : (0,5×2 = 1 pt)
G = \(4x^{2}-12x+9\)
H = \((5x+7)^{2}-16\)
5) Factoriser l’expression suivante, en justifiant les étapes : (0,75 pt)
M = \(x^{2}+2x-3\)
EXERCICE 2
(6 pts)
1) Choisir la bonne réponse : (0,5×2 = 1 pt)
a) L’égalité : \(x^{2}+2x+3=(x+1)(x+3)\), est vraie pour :
\(x=-7 \quad ; \quad x=2 \quad ; \quad x=0\)
b) Une solution de l’équation: \(x^{2}+x-\frac{3}{4}=0\) est :
\(-\frac{2}{5} \quad ; \quad \frac{1}{2} \quad ; \quad 1\)
2) Résoudre les équations suivantes : (0,75×4 = 3 pts)
\(x+7=2\)
\(-3x=9\)
\(\frac{x+7}{2}+\frac{x-9}{4}=\frac{2x-1}{8}\)
\(x(x-5)=(x-2)^{2}\)
Problème : (2 pts)
Pour un étudiant, une place de cinéma coûte 30 DH, alors que le prix normal est de 45 DH.
La recette pour 80 personnes a été de 3225 DH. Combien y avait-il d’étudiants parmi ces 80 personnes ?
EXERCICE 3
(8 pts)
Soit \(ABC\) un triangle tel que : \(AC = 6cm\) et \(\widehat{BAC} = 60°\).
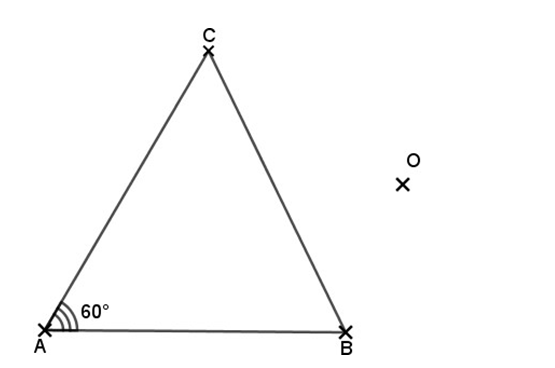
1) Sur la figure ci-dessus construire les points \(E, F\) et \(G\) les symétriques respectifs de \(A, B\) et \(C\) par rapport au point \(O\). (0,75×3 = 2,25 pts)
2) Construire le point \(M\) le milieu du segment \([AC]\), et \(N\) le symétrique de \(M\) par rapport à \(O\). (0,75×2 = 1,5 pts)
3) Montrer que \((AB) \parallel (EF)\). (1 pt)
4) Calculer la mesure de l’angle \(\widehat{FEG}\). (1 pt)
5) Calculer la distance \(EG\). (1 pt)
6) Montrer que \(N\) est le milieu du segment \([EG]\) (utiliser la définition du milieu). (1,25 pt)
🔒 Abonnez-vous pour accéder à la correction détaillée .
EXERCICE 1
(1 pt)
Réduire les expressions suivantes :
A = \(2x^2 + 4 + 4x + 5x^2 + 3x^2 – 2x – x\)
B = \(3a – 2b + 7b – 3a + 2b – 2 + 5a + 3b\)
EXERCICE 2
(5 pts)
Développer puis réduire les expressions suivantes :
C = \(3(x – 2) – 2(x + 5)\)
D = \(5(2x + 2)\)
E = \((x + 7)(x – 7)\)
F = \((5x – 6)(x – 3)\)
G = \((2x + 1)^2\)
EXERCICE 3
(4 pts)
Factoriser les expressions suivantes :
K = \(4x + 20\)
L = \(x(2 + x) + 3(2 + x)\)
M = \(x^2 – 14x + 49\)
N = \(25x^2 + 10x\)
EXERCICE 4
(4 pts)
Résoudre les équations suivantes :
\(3x + 4 = 0\)
\(5(x – 6) = 5\)
\(3(x + 2) = 6(x + 4)\)
\(\frac{5x}{4} = 3\)
EXERCICE 5
(2,5 pts)
Un père dispose de 1600 dh pour ses trois enfants, il veut que l’aîné ait 200 dh de plus que le second et que le second ait 100 dh de plus que le dernier.
Quelle somme doit-il donner à chacun ?
EXERCICE 6
(3,5 pts)
\(ABC\) est un triangle tel que \(AB = 7cm\), \(AC = 5cm\), \(\widehat{BAC} = 60^\circ\) et \(E\) un point de \([BC]\).
- 1. Faites une construction.
- 2. Tracer \(B’\), \(C’\) et \(E’\) les symétriques respectifs de \(B\), \(C\) et \(E\) par rapport à \(A\).
- 3. Montrer que \((BC) \parallel (B’C’)\).
- 4. Montrer que \(E’\), \(B’\) et \(C’\) sont alignés.
- 5. Calculer \(AB’\) et \(AC’\), justifier.
- 6. Calculer \(\widehat{B’AC’}\), justifier.
🔒 Abonnez-vous pour accéder à la correction détaillée .
EXERCICE 1
(2 pts)
Réduire les expressions suivantes :
A = \(2x^3 + 1 + 4x + 5x^3 – 2x – x\)
B = \(3a^2 – 2b + 7b^2 – b + 3a + 2ab – 2 + 5a + 3ab\)
EXERCICE 2
(5 pts)
Développer puis réduire les expressions suivantes :
C = \(5(x-3) – 3(x+3)\)
D = \(9(2x+5)\)
E = \(13x+6(3x-17)\)
F = \((x+4)(x-4)\)
G = \((5x-6)(x-3)\)
I = \((11a+5b)(11a-5b)\)
J = \((x-2)(2x-5)-7(-10x+4)\)
H = \((2x+1)^2+(x+2)(x-2)\)
EXERCICE 3
(4 pts)
Factoriser les expressions suivantes :
K = \(4x + 12\)
L = \(x(1-x) + 3(1-x)\)
M = \((5x+10) – x(x+2)\)
P = \((x-2)a+(x-2)b+(x-2)c\)
S = \(x^2 – 14x + 49\)
N = \(x^2 – 0,04\)
EXERCICE 4
(4 pts)
Résoudre les équations suivantes :
1) \(2x + 4 = 0\)
2) \(3(x-5) = 5\)
3) \(2x + 3 = 4x + 8\)
4) \(\frac{3x}{5} = 11\)
5) \(3(x+12) + 4x = 7(x+4)\)
EXERCICE 5
(3 pts)
\(ABC\) est un triangle rectangle en A, tel que \(AB = 4cm\), \(BC = 5cm\)
et \(\widehat{ABC} = 60^\circ\) et \(O\) un point dans le plan.
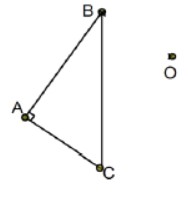
- 1. Tracer une construction.
- 2. Tracer \(E\), \(F\) et \(G\) les symétriques respectifs de \(A\), \(B\) et \(C\) par rapport à \(O\).
- 3. Calculer \(EF\) et \(FG\). Justifier.
- 4. Calculer \(\overrightarrow{EFG}\). Justifier.
- 5. Montrer que \((EF) \parallel (AB)\).
EXERCICE 6
(2 pts)
Calculer d’une façon plus simple :
a = \(102^2\)
b = \(301,495 \times 97 + 301,495 \times 3\)
c = \(9995 \times 1005\)
🔒 Abonnez-vous pour accéder à la correction détaillée .
Devoirs Corrigés Maths N°1 S2 1AC
