Devoirs Corrigés Maths N°1 S2 2AC
Modèle N°1
EXERCICE 1
(9 pts)
1) Réduire les expressions suivantes : (1+1=2 pts)
\(4x + 4 – 3x – 4 =\)
\(3x^{2} + 2x – x^{2} – 5x + 4 =\)
2) Développer et réduire les expressions suivantes : (1+1+1=3 pts)
\(4(x-3) =\)
\(-3(-x+8) + 5 =\)
\((x+1)(2x-4) =\)
3) Factoriser au maximum les expressions suivantes : (1+1+1+1=4 pts)
\(7x – 7y =\)
\(5x + 5 =\)
\(6x^{2} + 12x =\)
\(\frac{3}{5}x – \frac{7}{15}x^{2} =\)
EXERCICE 2
(9 pts)
1) Soit l’équation suivante \(2(x+1) + 14 = 10 + 5x\).
a) 0 est-il solution de l’équation ? (1 pt)
b) 2 est-il solution de l’équation ? (1 pt)
2) Résoudre les équations suivantes : (2+2=4 pts)
\(5x + 6 = -2x – 1\)
\(\frac{3}{4} + \frac{x}{2} = \frac{5}{8}\)
3) Déterminer la valeur de \(x\) pour que le périmètre du rectangle soit égal à 27 cm. (2 pts)
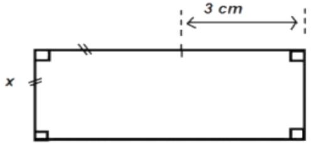
EXERCICE 3
(3 pts)
1) Développer : (0,5+0,5=1 pt)
\((a+b)^{2} =\)
\((x+\frac{2}{3})^{2} =\)
2) Factoriser : (0,5+0,5=1 pt)
\(a^{2} – b^{2} =\)
\(25 – x^{2} =\)
3) Déduire les solutions de l’équation \(25 – x^{2} = 0\). (1 pt)
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Modèle N°2
EXERCICE 1
(10 pts)
1) Développe puis réduis les expressions suivantes : (6×1 pts = 6 pts)
A = \(2x(1-x)\)
B = \(3x(5x-1)-2x(5x+2)\)
C = \((2x-1)(x+3)\)
D = \((3x-2)^{2}\)
E = \((x-3)(x+3)\)
F = \((2x-5)(2x+5)-(2x+3)^{2}\)
2) Factoriser les expressions suivantes : (4×1 pts = 4 pts)
G = \(36x^{2}+12x\)
H = \((x-\frac{9}{7})(x-3)+(x-\frac{9}{7})(x+10)\)
I = \(x^{2}-8x+16\)
J = \(9x^{2}-100\)
EXERCICE 2
(9 pts)
1) On donne l’expression suivante : \(E=16-(2x+3)^{2}\)
a) Développer et réduire \(E\).
b) Factoriser \(E\).
c) Calculer la valeur de \(E\) pour \(x=\frac{1}{2}\).
2) Soit \(x\) et \(y\) deux nombres rationnels :
• Montrer que : \((x+y)^{2}+(x-y)^{2}=2(x^{2}+y^{2})\)
EXERCICE 3
(3 pts)
MNP est un triangle rectangle en M tels que : MN = 4 cm et MP = 3 cm.
Soit C le milieu de [PN].
1) Faire une figure.
2) Quel est l’orthocentre du triangle MNP ?
3) Construire le point G centre de gravité du triangle.
4) Calculer MG sachant que : MC = 6 cm.
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Modèle N°3
EXERCICE 1
(8 pts)
1) Développe puis réduis les expressions suivantes :
A = \(6(-2x + 3) \)
B = \((3 + x)(2x – 5) \)
C = \((5 + x)^2 \)
D = \((3x – 1)(3x + 1) – (4x – 2)^2 \)
2) Factorise puis réduis les expressions suivantes :
A = \(12x + 4x^2 \)
B = \(16 – 9x^2 \)
C = \(36 + 24x + 4x^2 \)
D = \((x – 11)(2x + 10) – (3 – 7x)(x – 11) \)
EXERCICE 2
(8 pts)
1) Résoudre les équations suivantes :
\(x – 3 = 7\)
\(4x – 10 = 3\)
\(6x – 7 = 3x – 5\)
\(\frac{2x}{4} + \frac{x-5}{8} = \frac{5}{2}\)
\(\frac{9x – 11}{3} = 0\)
2) Trouve quatre nombres entiers consécutifs dont la somme vaut 1 254.
EXERCICE 3
(4 pts)
1) Comparer les nombres suivants :
\(\frac{2x+5}{2}\) et \(\frac{9+8x}{8}\)
2) Soient \(a\) et \(b\) deux nombres rationnels tel que : \(a < 9\) et \(b < 2\).
Comparer :
a) \(a + b \) et 11
b) \(-3b \) et -6
c) \(-2a+1 \) et -17
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Modèle N°4
EXERCICE 1
(8 pts)
1) Développe puis réduis les expressions suivantes : (6×0,5 pt = 3 pts)
A = \(2x(3x + 1) + 3x(-5x + 2)\)
B = \(-4x^2(-x – 7) – 5x(1 – 2x)\)
C = \((4x – 1)^2 + (5 – x)^2\)
D = \((3x – 2)(x – 4) – (2x – 3)^2\)
E = \(4x(x – 6)^2\)
F = \((5x – 2)(5x + 2) – (3x + 4)(3x + 4)\)
2) Factorise puis réduis les expressions suivantes : (7×0,5 pt = 3,5 pts)
A = \(24x^2 + 12x\)
B = \(25x – 15x^2\)
C = \((7x + 1)^2 – (5x – 3)(7x + 1)\)
D = \((2x + 3)(5x + 7) – (2x + 3)(-x – 1) + 2x + 3\)
E = \(144x^2 – 49\)
F = \(49 – 70x + 25x^2\)
G = \((2x – 3)(5x + 7) + 4x^2 – 9\)
EXERCICE 2
(5 pts)
Résoudre les équations suivantes :
(E₁) : \(10 – (x – 2) = 7 + (-5x + 4)\)
(E₂) : \(-3(2x – 1) + 7(1 – 5x) = 0\)
(E₃) : \(\frac{x}{2} + \frac{1}{3} = 5\)
(E₄) : \(\frac{1}{14} – \frac{2x – 1}{7} = \frac{x}{2}\)
(E₅) : \(7x^2 – 5x = 0\)
EXERCICE 3
(2 pts)
Quel nombre faut-il ajouter au numérateur et au dénominateur du nombre \(\frac{2}{7}\) pour obtenir le double du nombre \(\frac{2}{7}\) ?
EXERCICE 4
(5 pts)
1) Comparer les nombres suivants : (3×0,5 pt = 1,5 pts)
1) \(-\frac{7}{6}\) et \(-\frac{5}{4}\)
2) \(2x\) et \(\frac{7 + 8x}{4}\)
3) \(x(x – y)\) et \(y(x – y)\)
2) Soient \(a\) et \(b\) deux nombres rationnels tel que : \(a \geq 3\) et \(b \geq 1\). Montrer que : (3×1 pt = 3 pts)
1) \(a + b \geq 4\)
2) \(ab \geq 3\)
3) \(-2a + \frac{3}{4} \leq -\frac{21}{4}\)
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Modèle N°5
EXERCICE 1
(5 pts)
Développer et réduire les expressions suivantes :
A = \(9(x – 2)\)
B = \((2a + 3)(3a – 1)\)
C = \(\left( \frac{1}{4}x – 1 \right) \left( \frac{1}{4}x + 1 \right) – \frac{3}{4}x^2 + 1\)
EXERCICE 2
(6 pts)
Factoriser les expressions suivantes :
A = \(12x^3 + 8x^2 – 4x\)
B = \(9x^2 – 12x + 4\)
C = \(\frac{16}{25} – \frac{9}{64}y^2\)
D = \((x – 3)(5x – 1) + 9x – 27\)
EXERCICE 3
(9 pts)
Soit un cercle \( \mathcal{C} \) de rayon \( 2,5cm \) et de diamètre \([BC]\).
\( A \) est un point de \( \mathcal{C} \) tel que \( AB = 3cm \).
- 1. Construire la figure.
- 2. Montrer que le triangle \( ABC \) est rectangle.
- 3. Calculer \( AC \).
- 4. Calculer \( \cos \widehat{ABC} \).
- 5. \( H \) est le projeté orthogonal de \( A \) sur \( (BC) \).
- • Calculer \( BH \) .
Bon travail !
🔒 Abonnez-vous pour accéder à la correction détaillée de ce devoir.
Devoirs Corrigés Maths N°1 S2 2AC
