Devoirs Corrigés Maths N°2 S1 1AC
Modèle N°1
Exercice 1:$(0,5+0,5+0,5+0,5+1+1+1=5 pts)$
1) Calculer :
$A=(-8)+(+6)$
$\mathbf{B}=(-5,7)+(-3,8)$
$\mathbf{C}=24 -(\mathbf{- 1 3})$
$\mathbf{D}=34,7-50$
$\mathbf{E}=(-7)-12+(-5)$
$\mathrm{F}=\mathbf{9}-\mathbf{5 , 3}-(-5)-3,7$
$\mathbf{G}=-3+14+7-8-11$
Exercice 2:$(2 pts)$
Supprimer les parenthèses et le crochet et calculer l’expression suivante:
$H = 18 – (17 + 4 – 6 ) – [13 – (4 – 18 ) ]$
Exercice 3:$(1,5+1,5=3 pts)$
$a$ et $b$ deux nombres relatifs tels que : $a+b=-11 \quad$
Calculer :
$M=(\mathbf{a}-\mathbf{9}+\mathbf{4 5})-(5-b-45)$
$N=45,3-[7+b-(-30)]-(a+15,3)$
Exercice 4:$(0,5+0,75+0,75=2pts)$
Observer la figure puis compléter.
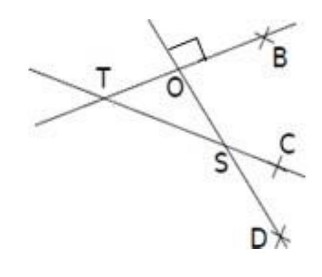
• Les deux angles $\mathbf{T} \hat{S} O$ et $………$ sont opposés par le sommet.
• Les deux angles $\mathrm{T} \hat{S} \mathrm{D}$ et $………$ sont supplémentaires.
• Les deux angles $………$ et $………$ sont complémentaires.
Exercice 5:$(1 +1+1+1=4 pts)$
On considère la figure ci-dessous :
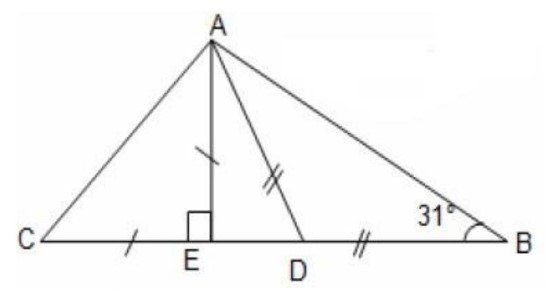
Calculer en justifiant votre réponse la mesure de chacun des angles suivants:
a- $C \widehat{A} \mathbf{E}$
b- $A \widehat{D} \mathbf{B}$
c- $E \widehat{A} \mathbf{D}$
d- $C \widehat{A} \mathbf{D}$
Exercice 6:$(1 +1+0,5+0,5+1=4 pts)$
a) Construire le triangle $MNP$ isocèle en $P$ tel que $\mathrm{MN}=4 \mathrm{~cm}$; $\mathbf{N} \widehat{\mathbf{M}} \mathbf{P}=70^{\circ}$
b) Calculer la mesure d’angle $\mathbf{M} \widehat{\boldsymbol{P}} \boldsymbol{N}$
c) Placer le point $H$ la projection orthogonale de $M$ sur la droite $(PN)$
d) Déterminer la nature du triangle $MNH$ ? justifier votre réponse
e) Calculer en justifiant votre réponse la mesure d’angle $\mathrm{H} \widehat{\boldsymbol{M}} \boldsymbol{N}$
Modèle N°2
Exercice 1:$(14 pts)$
1) Calculer les opérations suivantes: $(1 \times 6=6 pts)$
$(-4,3)+(-5) \quad ; \quad 17+(-7) \quad ; \quad(-8,5)+(-15)$
$5-(-8) \quad ; \quad 17,8-12,8 \quad ; \quad(-9)-(-5,4)$
2) Comparer les nombres relatifs suivants : $(0,5 \times 6=3 pts)$
$(-4,3) \ldots . .(-5)$
$15 ….. (-7) $
$(-8,5) \ldots . .(-15)$
$0 ….. (-8)$
$-17,8 …. .17,8$
$(-9)…. . (-5,4)$
3) Range dans l’ordre croissant : $(1 pt)$
$-5 \quad ; \quad -15 \quad ; \quad 0 \quad ; \quad -2,5 \quad ; \quad 2 \quad ; \quad 3,5 \quad ; \quad -13,51$
4) On considéré les abscisses des points suivants : $(1+2+1=4pts)$
$E(-3) \quad ; \quad F(2,5) \quad ; \quad G(-2) \quad ; \quad K(1,5)$
a) Place les points sur une droite graduée.
b) Calculer les distances $EF$ et $FG$.
c) Déterminer l’abscisse de $M$ sachant que $M$ est le milieu de $[EG]$.
Exercice 2:$(1,5+1+0,5+1+1+1=6pts)$
$IJK$ triangle rectangle en $I$ tel que : $\mathrm{IJ}=5 \mathrm{~cm}$ et $I \hat{\jmath} K=50^{\circ}$
1) Déterminer la valeur de $I \hat{J} K$ ? Justifier
2) Construire le triangle $IJK$.
3) Construire le point $A$ de demi-droite $[AJ)$ tel que $I$ est le milieu de $[AJ]$.
4) Que représente la droite $(IK)$ par rapport au segment $[AJ]$ ? Justifier
5) Donner la nature de triangle $AKJ$ ? Justifier
6) Déterminer la valeur de $\widehat{K A} J$ ? Justifier
Modèle N°3
Exercice 1:$(14 pts)$
1) Compléter par le signe » < » ou » > » :: $(1,5 pts)$
$+2,67 … 5,01$
$ -70,7 … – 1,5$
$+13 …- 23$
2) Ranger les nombres suivants dans l’ordre croissant: : $(1 pt)$
$-7,12 \quad ; \quad -19 \quad ; \quad 11 \quad ; \quad +3,1 \quad ; \quad 1 \quad ; \quad 0 \quad ; \quad -9,9 \quad ; \quad -11,01 $
3) On Considère la droite graduée ci-dessous : $(1+1=2 pt)$
a. Placer sur la droite les points .$A (-5)$, $\mathrm{B}(+3), \boldsymbol{C}(-2,5)$ et $D(+5)$ :

b. Calculer les distances $AB$ et $CD$ .
4) Calculer les expressions suivantes en écrivant les étapes intermédiaires : $(0,5+0,5+0,5+0,5+2=4pts)$
$(-3)+7 $
$-90 \div 45$
$(+2)-(-18) $
$(-18) \times(+0,5)$
$(-6)+(-6) \times(+2)+(-36) \div(-3)+3 \times(+2)$
5) Sachant que $a+b=-3$ et $a \times b=4$, calculer:$(0,75+0,75 =1,5 pt)$
• $1+a+(-5)+b+(+7) $
• $ a \times(-1) \times b-(-4)$
6) Supprimer les parenthèses puis effectuer les calculs : $(1 pt)$
$\mathrm{D}=-(-12-(+3-7))+(-12+4)$
Exercice 2:$(1+1+1=3 pts)$
Peut -on construire le triangle ABC dans les cas suivants? justifier ta réponse.
• $A B=7 \mathrm{~cm}, A \hat{B} C=95^{\circ}, B A \hat{ C}=87^{\circ}$
• $A B=3 \mathrm{dm} ; A C=4 \mathrm{~cm} ; B C=6 \mathrm{~cm}$
• $A B=5 \mathrm{~cm} ; A C=5 \mathrm{~cm} ; B \hat{A} C=60^{\circ} ; A \widehat{B} C=90^{\circ}$
Exercice 3:$(5 pts)$
1) Soit $A B C$ un triangle isocèle en $A$ tel que: $\mathrm{BC}=4 \mathrm{~cm}$ et $A \widehat{\mathrm{B}}C=\mathbf{5 0 ^ { \circ }}$$(1+1=2 pts)$
a) Construire la figure
b) Calculer la mesure de $B \widehat{A} C$ en justifiant
2) Observer la figure ci-dessous. tel que $E \widehat{O} L=90^{\circ}$ et $N \widehat{K}M=\mathbf{6 0} ^{\circ}$ et $F \widehat{O} L=\mathbf{13 0} ^{\circ}$ $(1+2=3 pts)$

a) Déterminer deux angles adjacents et opposés
b) Calculer la mesure de $F \widehat{O}G$ et $O \widehat{G} K$ en justifiant
Modèle N°4
Exercice 1:$(4,25 pts)$
$1)$ Placer sur une droite graduce les paints ci-apres enchoisissand bien l’échelle de graduation: $(0,25 \times 9=2,25 pts)$

$2)$ Ranger les abscisses de ses points par ordre croissant : $(2 pts)$
Exercice 2:$(3pts)$
Recopier at compléter par deux extiers relatifs consécutifs :
$ a) \ldots<-5,4<\ldots $
$ b) \ldots<-9,4<\ldots $
$ c) \cdots<19,51<\cdots$
$d) \cdots<-1,4<\ldots .$
$e) \cdots<29,4<\ldots .$
$f) \cdots<-8,1<\ldots .$
Exercice 3:$(1 \times 6=6 pts)$
Effectuer les calculs suivants :
$(+9)+(+36)$
$(-4,5)+(-9,4)$
$(-6)+(-17) $
$(-65)-(-10)$
$ (+10)+(-5)+(-16)$
$(+17)+(+13)+(-45)$
Exercice 4:$(0,25+0,5+1,5+1,5+3=6,75pts)$
$1)$ Tracer une droite $(D)$
$2)$ Placer deux points $A$ et $B$ tels que: $A$ et $B$ ne sont pas sur la droite $(D)$
$3)$ Tracer la parallèle ( $D^{\prime}$ ) à la droite ( $D$ ) passant par $A$
$4)$ Tracer la droite ( $D^{\prime\prime}$ ) passant par $B$ et perpendiculaire à la droite $(D)$
$5)v Que peut-on dire des droites ( $D^{\prime}$ ) et ( $D^{\prime\prime}$ ) ? Justifier
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Devoirs Corrigés Maths N°2 S1 1AC
