Devoirs Corrigés Maths N°2 S1 2AC
Modèle N°1
Exercice 1:(11 pts)
1) Calcule les expressions suivantes: : $(1 \times 7=7$ pts)
$\frac{11}{15}-\frac{3}{15} \quad ; \quad \frac{13}{2}-\left(\frac{-1}{3}\right) \quad ; \quad \frac{3}{9}-\frac{24}{27} \quad ; \quad \frac{14}{10}-\left(\frac{-1}{-5}\right)$
$\frac{3}{8} \div\left(\frac{-1}{9}\right) \quad ; \quad\left(\frac{-6}{5}\right) \times\left(-\frac{1}{13}\right) \quad ; \quad 1,5 \times\left(\frac{7}{-8}\right)$
2) Calcule l’expression suivante : $(2 \times 2=4$ pts)
$A=\frac{2}{3}-\left(\frac{-5}{4}\right)+\frac{1}{12} \quad $
$ B=\frac{2}{7}+\left(\frac{-1}{3}\right) \times\left(\frac{-11}{7}\right)-2$
Exercice 2:(3 pts)
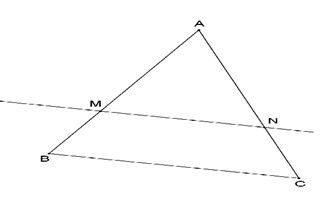
On considéré la figure suivante tel que:
$\mathrm{CN}=2 \mathrm{~cm} ; \mathrm{AB}=4 \mathrm{~cm}$; $\mathrm{AC}=4 \mathrm{~cm}$; $\mathrm{BC}=6 \mathrm{~cm}$ Et (BC) // (MN).
1) Calcule $AM$ et $ MN$. $(1,5 \times 2=3$ pts)
Exercice 3:$(1 +2+1+2 =6$ pts)
$ABC$ est un triangle tel que : $\mathrm{AB}=4 \mathrm{~cm} ; \mathrm{AC}=5 \mathrm{~cm}$; $\mathrm{BC}=7 \mathrm{~cm}$.
Soit $B^{\prime}$ le symétrique de $A$ par rapport au point $B$.
$C^{\prime}$ le symétrique de A par rapport au point C .
1) Construire une figure convenable.
2) Montrer que $(BC) // ( \left.B^{\prime} C^{\prime}\right)$.
3) Calculer la valeur de $B^{\prime} C^{\prime}$.
4) $G$ est le milieu du segment $[AC]$ et la droite $(D)$ passe par le point $G$ et parallèle à la droite $(BC)$ et coupe le segment $[AB]$ au point $E$.
• Montrer que le point $E$ est le milieu de $[AB]$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°2
Exercice 1:(13 pts)
1) Remplace les pointilles par ce qui convient: ( $a, b$ et $c$ sont des nombres rationnels non nuls et $\boldsymbol{n}, \boldsymbol{m}$ sont des nombres entiers naturels ).: $(0,5 \times 11=5,5$ pts)
$a \times \frac{b}{c}=\ldots \ldots \ldots \ldots .$
$\frac{\frac{\mathrm{a}}{\mathrm{~b}}}{\mathrm{c}}=\ldots \ldots \ldots \ldots .$
$\frac{a}{\frac{b}{c}}=\ldots \ldots \ldots \ldots .$
$ \mathbf{a}^{0}= \ldots \ldots \ldots \ldots .$
$ \left(a^{n}\right)^{m}= \ldots \ldots \ldots \ldots .$
$ \frac{1}{a^{-n}}=\ldots \ldots \ldots \ldots .$
$a^{n} \times a^{m}=\ldots \ldots \ldots \ldots .$
$\frac{a^{n}}{a^{m}}=\ldots \ldots \ldots \ldots .$
$a^{n} \times b^{n}=\ldots \ldots \ldots \ldots$.
$\frac{a^{n}}{b^{n}}=\ldots \ldots \ldots \ldots $
$\left(\frac{a}{b}\right)^{-m}=\ldots \ldots \ldots \ldots $
2) Calculer et simplifier si possible les expressions suivantes: $(0,5 \times 9=4,5$ pts)
$\frac{-7}{3} \times \frac{15}{21}$
$\frac{-6}{11} \div \frac{2}{-5}$
$\left(\frac{-1}{5}-\frac{8}{3}\right) \times \frac{5}{4} \div 7$
$\frac{7-\frac{3}{5}}{\frac{2}{10}}$
$\left(\left(\frac{1}{2}\right)^{-3}\right)^{6}$
$\frac{11^{-2}}{11^{7}}$
$9^{2} \times 3^{8}$
$\left(\frac{2}{5}\right)^{-4}$
$\frac{(\frac{7}{4})^{5}}{(\frac{13}{4})^{5}}$
3) a-Simplifier les expressions suivantes ( $a$ et b sont deux nombres rationnels non nuls). $(1 \times 2=2$ pts)
$A=\frac{5^{-4} \times 5^{7}}{2^{3} \times 5^{3}}$
$B=\frac{\frac{1}{a}+\frac{1}{b}}{a+b}$
b – Prouver que $\frac{a+b}{c}+\frac{b+c}{a}+\frac{a+c}{b}=-3$, sachant que $a b+b c+a c=0$ $(1 pt)$
Exercice 2: $(1 \times 7=7$ pts)
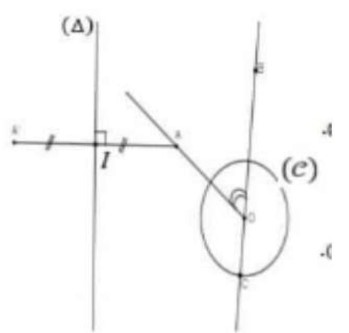
On considère Ia figure ci-contre tels que : $A O=3 \mathrm{~cm}, O C=1.5 \mathrm{~cm}$ et $\widehat{A^{\prime} OB }=35^{\circ}$
1) Montrer que $A’$ est le symétrique de $A$ par rapport à ( $\Delta$ )
2) Construire $O^{\prime}, B^{\prime}, C^{\prime}$ les symétriques (respectivement) de $\mathrm{O}, \mathrm{B}, \mathrm{C}$ par rapport à ( $\Delta$ ).
3) Montrer que $ A^{\prime} O^{\prime}=3 \mathrm{~cm}$.
4) Quel est le symétrique du point $I$, de la droite $(BI)$ et de demi droite $(IC]$ par rapport à ( $\Delta$ ) . Justifier
5) Montrer que les points $O^{\prime}, B^{\prime}$ et $C^{\prime}$ sont alignées
6) Déterminer la mesure de l’angle $\widehat{AO^{\prime}B^{\prime} }$. Justifier
7) Construire le symétrique de la cercle de $(C)$ par rapport à ( $\Delta$ ).
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°3
Exercice 1:(8 pts)
1) Développer et réduire:: $(1 \times 4=4$ pts)
a) $\frac{5}{3}(2 x-\frac{1}{4}) $
b) $-2(\frac{3}{2} x-\frac{1}{4})$
c) $-\frac{1}{6} \times(\frac{4}{6}-\frac{4}{3})$
d) $-\frac{3}{5}(\frac{4 x}{3}-\frac{7}{2})$
2) Calculer : $(1 \times 4=4$ pts)
$I=\frac{1}{8}+\frac{5}{\frac{6}{7}}$
$J=\frac{\frac{7}{4}-\frac{1}{6}}{\frac{8}{3}} $
$K=\frac{7}{8} \div \frac{5}{3} $
$L=\frac{\frac{3}{4}}{\frac{1}{8}}$
Exercice 2:($1 \times 5=5$ pts)
Calculer en simplifiant si possible:
a) $\frac{25}{16} \times \frac{24}{45}$
b) $\frac{9}{20} \times \frac{16}{9}$
c) $\frac{2}{4} \times \frac{3}{5}-\frac{7}{10}$
d) $\frac{2 \times 3 \times 7}{3 \times 5 \times 17 \times 2}$
e) $\frac{17+3}{11} \times \frac{23-1 2}{20}+\frac{1}{2}$
Exercice 3:($2+2+3 =7$ pts)
I- $A B C D$ un rectangle, $I, J$ les milieux des segments $[A B]$ et $[D C]$ respectivement.
a) Quels sont les symétriques des points $B$, $C$ par rapport à la droite $(IJ)$.
b) $K$ appartient à la droite $(IJ)$. quelle est la nature du triangle $D K C$, Justifier.
II- $ABC$ un triangle rectangle en $A$.
$A^{\prime} , B^{\prime} et C^{\prime}$ symétriques des points $A, B$ et $C$ (respectivement) par rapport à la droite (d).
• Quelle est la nature du triangle $A^{\prime} B^{\prime} C^{\prime}$. Justifier

🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°4
Exercice 1:(10 pts)
1) Calculer puis simplifier si possible : $(1 \times 4=4$ pts)
$\mathrm{A}=\frac{-1}{8} \times \frac{7}{-9}$
$\mathrm{~B}=\frac{-2}{5} \times \frac{7}{-12} \quad$
$\mathrm{C}=\frac{-12}{-11} \div \frac{4}{-33}$
$\mathrm{D}=\frac{-19}{10} \div 19$
2) Calculer puis simplifier si possible : $(1 \times 3=3$ pts)
$A=\frac{-2}{7} \times \frac{-3}{5} \times \frac{1}{6}$
$B=\frac{-17}{13} \times \frac{15}{11} \times \frac{13}{17}$
$C=8 \times \frac{-13}{5} \times \frac{1}{13}$
3) $a$ et $b$ désignent deux nombres rationnels avec $a \times b=\frac{5}{3}$
Calculer les produits suivants : $(1 \times 3=3$ pts)
• $5 b \times (-\frac{6}{25} a)$
• $-3 a \times 5 b$
• $(a \times \frac{-7}{3}) \times b$
Exercice 2:(4 pts)
1) Calculer les puissances suivantes: ($0,5 \times 4=2$ pts)
• $\left(\frac{-1}{7}\right)^{3}$
• $\left(\frac{-1}{6}\right)^{-2}$
• $\left(\frac{-1}{2}\right)^{4}$
• $\left(\frac{-3}{5}\right)^{-3}$
2) Donner le signe des nombres suivants: ($0,5 \times 4=2$ pts)
• $\left(\frac{-1}{12}\right)^{6}$
• $\left(\frac{-3}{7}\right)^{5}$
• $\left(\frac{-2}{-4}\right)^{7}$
• $-4^{6}$
Exercice 3: ($1 \times 5=5$ pts)
$ABC$ est un triangle rectangle et isocèle en $A$.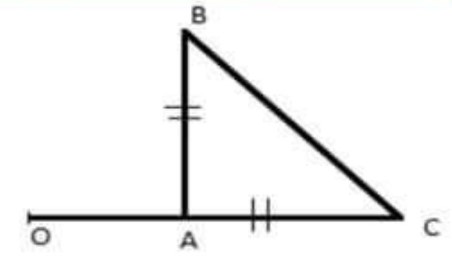
1) Construire le point $E$ le symétrique du point $A$ par rapport à la droite $(BC)$.
Construire le point $F$ le symétrique du point $O$ par rapport à la droite $( BC )$.
2) Montrer que les points $\mathrm{C}, \mathrm{E}$ et $F$ sont alignés.
3) Quel est le symétrique du segment $[\mathrm{OB}]$ par rapport à la droite $(BC)$? Justifier.
4) Quel est le symétrique de l’angle $A \hat{B} C$ par rapport à la droite $(\mathrm{BC})$ ? Justifier.
5) Déduire la mesure de l’angle $\mathrm{E} \hat{B} C$.
Exercice 4:(1 pts)
$a$ et $b$ deux nombres rationnels avec $a \times b=\frac{7}{8}$.
• Calculer $\quad \frac{a+b}{\frac{1}{a}+\frac{1}{b}}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Devoirs Corrigés Maths N°2 S1 2AC
