Devoirs Corrigés Maths N°2 S1 3AC
Modèle N°1
Exercice 1:$(1+1+1+2=5$ pts)
1) Simplifie : $\frac{3}{\sqrt{5}-\sqrt{2}}-\frac{2}{\sqrt{2}}$
2) Comparer les nombres suivants: $7 \sqrt{3}$ et $5 \sqrt{6}$
3) Déduire de la question précédente une écriture simplifiée de l’expression :
$A=\sqrt{(7 \sqrt{3}-5 \sqrt{6})^{2}}$
4) Comparer : $\frac{1}{4 \sqrt{2}}$ et $\frac{1}{2 \sqrt{7}}$
Exercice 2:$(3+3+1=7$ pts)
Soit $a$ et $b$ deux nombres réels tels que :
$7 \leq b \leq 10 \quad \text { et } \quad-7 \leq a \leq-2$
1) Donner un encadrement de : $a+b \quad $ ; $a-b \quad ;-2 a+2 b$
2) Donner un encadrement de : $a b \quad ; \frac{a}{b} \quad ; \frac{2 a-b}{a+b}$
3) Comparer les nombres suivants : $a+7 \sqrt{3}$ et $b+5 \sqrt{6}$
Exercice 3:$(1 + 1+ 1=3$ pts)}
Soit un triangle $EDF$ rectangle en $D$.
1) Écris l’égalité de Pythagore pour ce triangle.
2) On donne : $\mathrm{EF}=5 \mathrm{~cm}$ et $\mathrm{DF}=4\mathrm{~cm}$. Calculer la longueur $ED$.
3) Calculer $DF$ avec $\mathrm{EF}=10$ et $\mathrm{ED}=6$.
Exercice 4:$(1 + 2+ 2 = 5$ pts)}
$ABCD$ est un rectangle tel que : $\mathrm{AB}=5$ et $\mathrm{BC}=2$.
$E$ est un point qui appartient au segment $[CD]$ tel que $C E=B C$.
La droite $(AE)$ coupe $(BC)$ en $F$.
1) Comparer $\frac{A B}{C E}$ et $\frac{F B}{F C}$
2) Déduire la valeur de $FC$.
3) Soit I un point du $[EF]$ tel que $EI = 1$.
J un point du $[AE] $ tel que $EJ = 1,5$.
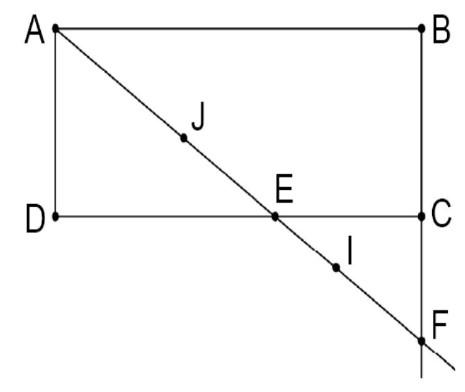
• Montrer que $(DJ) // (CI)$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°2
Exercice 1:$(6+2=8$ pts)
1) Comparer les nombres suivants (justifier votre réponse)
$\frac{7}{3} \quad $ et $ \quad \frac{5}{6}$
$\frac{3}{7} \quad $ et $ \quad \frac{6}{5}$
$3 \sqrt{7} \quad $ et $ \quad 7 \sqrt{3}$
$\frac{7}{3}+\sqrt{5} \quad $ et $ \quad \frac{5}{6}+\sqrt{5}$
$\sqrt{3 \sqrt{7}+1} \quad $ et $ \quad \sqrt{7 \sqrt{3}+1}$
$3 \sqrt{7} \times(-2)^{5} \quad $ et $ \quad 7 \sqrt{3} \times(-2)^{5}$
2) Soient $x$ et $y$ deux nombres réels tel que : $5 x+3 \sqrt{7}=5 y+7 \sqrt{3}$
• Comparer $x$ et $y$
Exercice 2:$(2+4=6$ pts)
Soient, a b et $\mathbf{c}$ trois nombres réels tels que : tels que : $2 \leq a \leq 4,-3 \leq b \leq-1$ et $\mathbf{5 \leq 2 c – 1 \leq 9 }$
1) Montrer que : $\mathbf{3 \leq c \leq 5}$
2) Encadrer : $a+b \quad $ ; $a-b \quad $ ; $ab \quad $ ; $\frac{\mathrm{a}}{\mathrm{c}}$
Exercice 3:$(1+1+2+2=6$ pts)
On considère la figure ci-contre telle que : $O M=1,6$; $O B=2,4$; $O C=\frac{2}{3} O D$
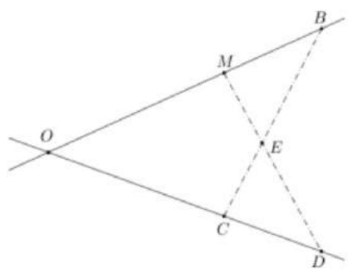
1) a- Montrer que $\frac{O C}{O D}=\frac{2}{3} \quad$
b- Calculer $\frac{O M}{O B} $
c- Déduire que $(MC) / /(B D)$
2) Utiliser le théorème direct de Thalès pour montrer que $3EM= 2ED$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°3
Exercice 1:$(1,5+1,5=3$ pts)
Calculer et simplifier les expressions suivantes:
$A=\left[\frac{1}{\sqrt{3}+\sqrt{2}}\right]^{-2} $
$B=\frac{1}{3-\sqrt{6}}-\frac{\sqrt{2}}{\sqrt{3}}$
Exercice 2:$(1,5+4+1+1,5=8$ pts)
1) Comparer: $4 \sqrt{5}$ et $6 \sqrt{2}$ puis en déduire une comparaison de: $7-4 \sqrt{5}$ et $7-6 \sqrt{2}$
2) $x$ et $y$ sont deux nombres réels tels que:
$2 \leq \sqrt{3 x+1} \leq \sqrt{10} \quad $ ; $ \quad -2 \leq y \leq-1$
a- Montrer que : $1 \leq x \leq 3$
b- Encadrer: $x+y \quad $ ; $ 3 x-y \quad $ ; $ \quad \frac{y^{2}+5}{y}$
3) $a$ et $b$ sont deux nombres réels positifs tels que :
$2 \leq \sqrt{b+1} \leq 3 \quad $ et $ \quad 0 \leq \frac{a^{2}-1}{3} \leq 1$
• Montrer que: $\quad 3 \leq a b \leq 16$
4) $x, y$ et $z$ sont des nombres réels strictement positifs
a- Développer: $\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2}$
b- En déduire que : $x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 6$
Exercice 3:$(1+1+1=3$ pts)
$A B C$ est un triangle rectangle en $A$ tel que :
$A B=2 \sqrt{5} \text { et } A C=4$
1) Calculer la longueur $B C$
2) Calculer l’aire du triangle $A B C$
3) Soit H le projeté orthogonal du point A sur la droite (BC)
• Montrer que: $A H=\frac{4 \sqrt{5}}{3}$
Exercice 4:$(2+2+1=5$ pts)
$A B C$ est un triangle tel que :
$B C=6 \mathrm{~cm} ; A C=3 \mathrm{~cm} ; A B=4 \mathrm{~cm}$
Soit $M$ un point du côté $[A B]$ tel que : $B M=3 \mathrm{~cm}$
La droite parallèle à la droite ( AC ) passant par le point M coupe le côté $[B C]$ au point N (voir la figure).
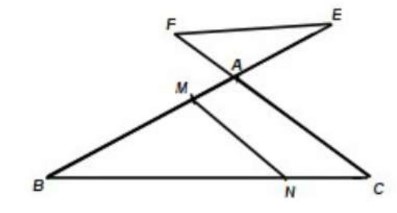
1) Calculer les longueurs $M N$ et $B N$
2) Soit E le point de la demi-droite $[B A$ ) tel que:
$B E=6 \mathrm{~cm}$
Soit F le point de la demi-droite (CA) tel que:
$C F=4,5 \mathrm{~cm}$
a– Montrer que: $(E F) / /(B C)$
b- Sans calculer la distance EF, montrer que:
$E F=\frac{2}{3} B N$
Exercice 5:$(1$ pt)
On considère l’expression suivante :
$B =\frac{2(\sqrt{2}+\sqrt{6})}{3 \sqrt{2+\sqrt{3}}} $
• Montrer que : $B =\frac{4}{3}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°4
Exercice 1:$(1,5+1,5+1=4$ pts)
1) Simplifier: $\frac{3}{\sqrt{5}-\sqrt{1}}-\frac{2}{\sqrt{2}}$
2) Comparer les nombres suivaris: $7 \sqrt{3}$ et $5 \sqrt{6}$
3) Deduire de la question précedente une écriture simplifier de l’expression: $A=\sqrt{(7 \sqrt{3}-5 \sqrt{6})^{2}}$
Exercice 2:$(2+3+4=9$ pts)
1) a un nombre rél tel que: $a \geqslant 7$
a) Montrer que: $-2 a+1 / 4 \leqslant 0$
b) Montrer que: $-\frac{7}{a} \geqslant-3$
2) $a$ et $b$ deux réels positifs: $a<b$
a) Moutrer que: $2 a<a+b$
b) Deduire que: $a<\frac{a+b}{t}$
c) Montrer que: $a<\frac{a+b}{c}<b$
3) $x$ et $y$ deur réls tels que: $-4<y<-2$ et $3<x<5$
Donner un encadrement de: $x+y ; x-y ; x^{2}+ y^{2} ; \frac{x}{y} $
Exercice 3:$(2+3+2=7$ pts)
Soit $A B C$ un triangle tel que: $A B=8 \mathrm{~cm}, A C=6 \mathrm{~cm}, B C=4$
$E$ un point du segment $[A B]$ tel que: $A E=2$.
La droite passant par $E$ parallilement à $(B C)$ coupe $(AC)$ en $F$.
1) Construire la figure
2) Calculer : $AF$ et $EF$
3) $I \in[B A)$ tel que: $B I=10 \mathrm{~cm}, et J \in[C A)$ tel que: $CJ= 7,5 \mathrm{~cm}$.
• Montrer que $(I J) // (B C)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Modèle N°5
Exercice 1
8 points
1- Comparer : \( 4\sqrt{5} \) et \( 6\sqrt{2} \) puis en déduire une comparaison de :
\[7 – 4\sqrt{5} \quad \text{et} \quad 7 – 6\sqrt{2}\]
2- \( x \) et \( y \) deux nombres réels tels que :
\[2 \leq \sqrt{3x + 1} \leq \sqrt{10} \quad \text{et} \quad -2 \leq y \leq -1\]
a) Montrer que : \( 1 \leq x \leq 3 \)
b) Encadrer : \( x + y \); \( 3x – y \); \( \frac{x^2 + 5}{y} \)
3- \( a \) et \( b \) sont deux nombres réels positifs tels que :
\[2 \leq \sqrt{b + 1} \leq 3 \quad \text{et} \quad 0 \leq \frac{a^2 – 1}{3} \leq 1\]
Montrer que : \( 3 \leq ab \leq 16 \)
Exercice 2
6 points
\( ABC \) est un triangle et \( K \) le projeté orthogonal du point \( A \) sur la droite (\( BC \)).
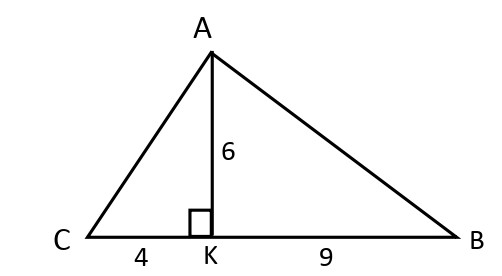
1- Calculer : \( AB \) et \( AC \)
2- Montrer que \( ABC \) est un triangle rectangle parallèles
Exercice 3
6 points
On considère la figure suivante telle que :
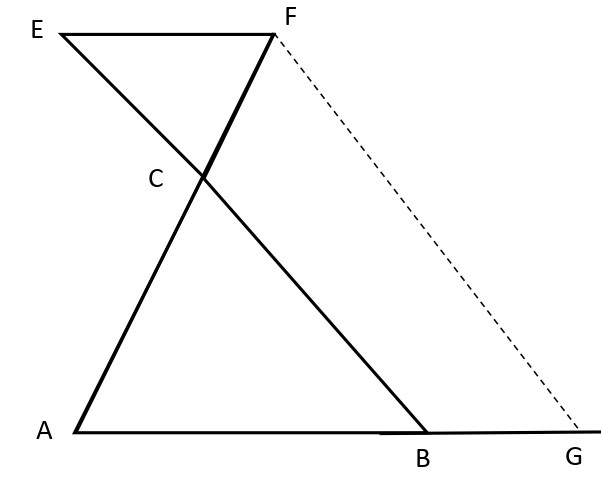
\[(EF) \quad // \quad (AB)\]
\[CF = 3 \quad ; \quad AC = 6\]
\[BC = 4 \quad ; \quad AB = 8\]
1- Calculer : \( CE \) et \( EF \)
2- \( G \) est un point de la demi-droite \([AB]\) tel que : \( BG = 4\)
Montrer que les droites (\( BC \)) et (\( FG \)) sont parallèles
Exercice 4
Bonus
\( x, \, y \) et \( z \) sont des nombres réels strictement positifs.
1- Développer :
\[\left( \sqrt{x} – \frac{1}{\sqrt{x}} \right)^2\]
2- En déduire que :
\[x + y + z + \frac{1}{x} + \frac{1}{y} + \frac{1}{z} \geq 6\]
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Devoirs Corrigés Maths N°2 S1 3AC
