Devoirs Corrigés Maths N°2 S1 Tronc commun
Modèle N°1
Questions indépendantes:$(1×5=5 pts)$
$1)$ Déterminer les entiers relatifs qui vérifient la relation suivante : $|-2 x+3|<6$
$2)$ Montrer que le nombre: $(\sqrt{6}-\sqrt{2}) 2 \sqrt{2}(\sqrt{3}+1)$ est entier naturel.
$3)$ On considère les deux nombres : $a=\sqrt{10}$ et $b=\sqrt{5}+\sqrt{2}-1$
$a$- Vérifier que : $a-b=(\sqrt{5}-1)(\sqrt{2}-1)$
$b$- En déduire une comparaison de $a$ et $b$
$4)$ Simplifier l’expression suivante : $B=|1-\sqrt{3}|+|\sqrt{18}-4 \sqrt{2}|-\sqrt{3}-\sqrt{2}$
Exercice 1:$(1+1+1,5+1=4,5 pts)$
$A B C$ un triangle et $D$ le point tel que : $\overrightarrow{B D}=\frac{1}{3} \overrightarrow{B C}$
• Le point $\boldsymbol{E}$ est le projeté de $\boldsymbol{D}$ sur $(\boldsymbol{A C})$ parallèlement à ( $\boldsymbol{A B} $ )
• Le point $\boldsymbol{F}$ est le projeté de $\boldsymbol{E}$ sur $(\boldsymbol{B C})$ parallèlement à ( $\boldsymbol{A D})$
$1)$ Construire la figure.
$2)$ Montrer que $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A C}$ et $\overrightarrow{D F}=\frac{1}{3} \overrightarrow{D C}$
$3)$ Montrer que $\frac{C D}{C B}=\frac{E D}{A B}$ et $\frac{C D}{C F}=\frac{A D}{E F}$
$4)$ Déduire que : $\overrightarrow{B F}=\frac{1}{3}(\overrightarrow{B C}+\overrightarrow{D C})$
Exercice 2:$(1+2+0,5+1×2=5,5 pts)$
Soit $a$ et $b$ deux nombres réels tels que: $|a-1|<\frac{1}{2}$ et $\left|b-\frac{1}{2}\right|<\frac{1}{6}$
$1)$ Montrer que : $\frac{1}{2}<a<\frac{3}{2}$ et $\frac{1}{3}<b<\frac{2}{3}$
$2)$ Encadrer chacun des nombres : $\boldsymbol{a}-\boldsymbol{b}$ et $\frac{\boldsymbol{a}}{\boldsymbol{b}}$ et $-\mathbf{3 a b}$ et $\sqrt{\boldsymbol{a b}}$
$3)$ Développer $(a+2)^{3}$
$4)$ On pose : $A=(a+2)^{3}-(6+a) a^{2}$
• Vérifier que : $A=8+12 a$, en déduire un encadrement de $A$.
Exercice 3:$(1×3=3 pts)$
Soient $x$ et $y$ deux nombres réels tels que : $x \leq \frac{1}{2}, y \geq \frac{3}{4}$ et $x-2 y=5$
On pose : $A=\sqrt{x^{2}+(x-1)^{2}+2 x(x-1)}$ et $B=\sqrt{4 y^{2}+(2 y-3)^{2}+4 y(2 y-3)}$
$1)$ Montrer que : $A=\sqrt{(2 x-1)^{2}}$ et $B=\sqrt{(4 y-3)^{2}}$
$2)$ Simplifier les nombres $\boldsymbol{A}$ et $\boldsymbol{B}$
$3)$ Déterminer la valeur numérique du nombre $\boldsymbol{A}+\boldsymbol{B}$
Exercice 4:$(2pts)$
Soit $x$ un nombre réel strictement positif tel que : $\sqrt{x}+\frac{1}{\sqrt{x}}=\sqrt{5}$
• Montrer que : $\left|\sqrt{\boldsymbol{x}}-\frac{1}{\sqrt{x}}\right|=\mathbf{1}$
$1)$ Déterminer les entiers relatifs qui vérifient la relation suivante : $|-2 x+3|<6$
On a: $|-2 x+3|<6 $
Alors : $-6<-2 x+3<6 $
Donc : $-9<-2 x<3 $
Donc : $-\frac{3}{2}<x<\frac{9}{2}$
$2)$ Montrer que le nombre: $(\sqrt{6}-\sqrt{2}) 2 \sqrt{2}(\sqrt{3}+1)$ est entier naturel.
$(\sqrt{6}-\sqrt{2}) 2 \sqrt{2}(\sqrt{3}+1)=2(\sqrt{6}-\sqrt{2})(\sqrt{6}+\sqrt{2}) =2\left((\sqrt{6})^{2}-(\sqrt{2})^{2}\right)=2(6-2)=8 \in \mathbb{N}$
$3)$ On considère les deux nombres : $a=\sqrt{10}$ et $b=\sqrt{5}+\sqrt{2}-1$
$a)$ Vérifier que : $a-b=(\sqrt{5}-1)(\sqrt{2}-1)$
$a-b=\sqrt{10}-\sqrt{5}-\sqrt{2}+1=\sqrt{5} \times \sqrt{2}-\sqrt{5}-\sqrt{2}+1$
$a-b=\sqrt{5}(\sqrt{2}-1)-(\sqrt{2}-1)=(\sqrt{5}-1)(\sqrt{2}-1)$
$b)$ On a: $\sqrt{5}>1$ et $\sqrt{2}>1$
Alors : $(\sqrt{5}-1)(\sqrt{2}-1)>0$
Puisque : $a-b>0$
Donc : $\boldsymbol{a}>\boldsymbol{b}$
$4)$ Simplifier l’expression suivante : $B=|1-\sqrt{3}|+|\sqrt{18}-4 \sqrt{2}|-\sqrt{3}-\sqrt{2}$
$B=|1-\sqrt{3}|+|\sqrt{18}-4 \sqrt{2}|-\sqrt{3}-\sqrt{2}$
• $|1-\sqrt{3}|=\sqrt{3}-1 \text { car }: 1-\sqrt{3}<0$
• $|\sqrt{18}-4 \sqrt{2}|=4 \sqrt{2}-\sqrt{18} \text { car }: \sqrt{18}<4 \sqrt{2}$
Donc: $B=\sqrt{3}-1+4 \sqrt{2}-\sqrt{18}-\sqrt{3}-\sqrt{2}$
$B=\sqrt{3}-1+4 \sqrt{2}-3 \sqrt{2}-\sqrt{3}-\sqrt{2}$
$B=4 \sqrt{2}-4 \sqrt{2}-1$
$B=-1$
$1)$ Construire la figure.
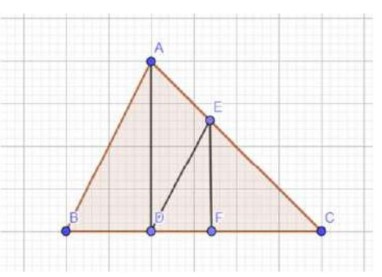
$2)$ Montrer que $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A C}$ et $\overrightarrow{D F}=\frac{1}{3} \overrightarrow{D C}$
• On a :
$E$ est le projeté de $D$ sur $(\mathrm{AC})$ parallèlement à $(\mathrm{AB})$
$A$ est le projeté de $B$ sur $(\mathrm{AC})$ parallèlement à $(AB)$
$C$ est le projeté de $C$ sur $(A C)$ parallèlement à $(AB)$
Et $\quad \overrightarrow{B D}=\frac{1}{3} \overrightarrow{B C}$
Puisque la projection conserve le coefficient de colinéarité.
Donc : $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A C}$
• On a :
$F$ est le projeté de $\mathbf{E}$ sur $(BC)$ parallèlement à $(AD)$
$D$ est le projeté de $A$ sur $(BC)$ parallèlement à $(AD)$
$C$ est le projeté de $C$ sur $(BC)$ parallèlement à $(AD)$
Et $\overrightarrow{A E}=\frac{1}{3} \overrightarrow{A C}$
Puisque la projection conserve le coefficient de colinéarité.
Donc: $\overrightarrow{D F}=\frac{1}{3} \overrightarrow{D C}$
$3)$ Montrer que $\frac{C D}{C B}=\frac{E D}{A B}$ et $\frac{C D}{C F}=\frac{A D}{E F}$
• Dans le triangle $ABC$ les droites $(D E) / /(B A)$
Alors d’après le théorème direct de Thalès :
$\frac{C D}{C B}=\frac{E D}{A B}$
• Dans le triangle $ADC$ les droites $(AD)//(EF)$
Alors d’après le théorème direct de Thalès :
$\frac{C D}{C F}=\frac{A D}{E F}$
$4)$ Déduire que : $\overrightarrow{B F}=\frac{1}{3}(\overrightarrow{B C}+\overrightarrow{D C})$
On a : $\overrightarrow{B F}=\overrightarrow{B D}+\overrightarrow{D F}$
$ \overrightarrow{B F} =\frac{1}{3} \overrightarrow{B C}+\frac{1}{3} \overrightarrow{D C}$
$ \overrightarrow{B F} =\frac{1}{3}(\overrightarrow{B C}+\overrightarrow{D C})$
$1)$ Montrer que : $\frac{1}{2}<a<\frac{3}{2}$ et $\frac{1}{3}<b<\frac{2}{3}$
• On a : $|a-1|<\frac{1}{2}$
Alors : $-\frac{1}{2}<a-1 <\frac{1}{2}$
$-\frac{1}{2}+1 <a<\frac{1}{2}+1 $
Donc : $\frac{1}{2} <a <\frac{3}{2}$
• On a : $\left|b-\frac{1}{2}\right|<\frac{1}{6}$
Alors : $\left|b-\frac{1}{2}\right|<\frac{1}{6} $
$-\frac{1}{6}<b-\frac{1}{2}<\frac{1}{6} $
$-\frac{1}{6}+\frac{1}{2}<b<\frac{1}{6}+\frac{1}{2} $
Donc : $ \frac{1}{3}<b<\frac{2}{3}$
$2)$
• Encadrons : $\boldsymbol{a}-\boldsymbol{b}$
$ \frac{1}{2}<a<\frac{3}{2} $
$ \frac{1}{3}<b<\frac{2}{3}$
$\frac{1}{2}-\frac{2}{3}<a-b<\frac{3}{2}-\frac{1}{3} $
$-\frac{1}{6}<a-b<\frac{7}{6}$
• Encadrons : $\frac{\boldsymbol{a}}{\boldsymbol{b}}$
$\frac{1}{2}<a<\frac{3}{2}$
$\frac{1}{3}<b<\frac{2}{3}$
$\frac{1}{\frac{2}{2}}<\frac{a}{b}<\frac{\frac{3}{2}}{\frac{1}{3}}$
$\frac{3}{4}<\frac{a}{b}<\frac{9}{2}$
• Encadrons : $-\mathbf{3 a b}$
$\frac{1}{2}<a<\frac{3}{2}$
$\frac{1}{3}<b<\frac{2}{3}$
$\frac{1}{6}<a b<1$
$-3<-3 a b<-\frac{1}{2}$
• Encadrons : $\sqrt{\boldsymbol{a b}}$
$\frac{1}{2}<a<\frac{3}{2}$
$\frac{1}{3}<b<\frac{2}{3}$
$\frac{1}{6}<a b<1$
$\frac{1}{\sqrt{6}}<\sqrt{a b}<1$
$\frac{\sqrt{6}}{6}<\sqrt{a b}<1$
$3)$ Développer $(a+2)^{3}$
On sait que : $(a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}$
Alors :
$(a+2)^{3}=a^{3}+3 a^{2} \times 2+3 a \times 2^{2}+2^{3}$
Donc :
$(a+2)^{3}=a^{3}+6 a^{2}+12 a+8$
$4)$
• Vérifier que : $A=8+12 a$
$A=a^{3}+6 a^{2}+12 a+8-6 a^{2}-a^{3}$
$A=12 a+8$
• L’encadrement de A:
On a $\quad \frac{1}{2}<a<\frac{3}{2}$
$6<12 a<18 $
$14<12 a+8<26$
$1)$ Montrer que : $A=\sqrt{(2 x-1)^{2}}$ et $B=\sqrt{(4 y-3)^{2}}$
On a : $A=\sqrt{x^{2}+(x-1)^{2}+2 x(x-1)}$
$x^{2}+(x-1)^{2}+2 x(x-1)=(x+(x-1))^{2}$, Identité remarquable: $(a+b)^{2}=a^{2}+2 a b+b^{2}$
Alors: $ A=\sqrt{(2 x-1)^{2}}$
On fait la même chose pour $B$ on trouve.
$B=\sqrt{(2 y+(2 y-3))^{2}}=\sqrt{(4 y-3)^{2}}$
$2)$ Simplifier les nombres $\boldsymbol{A}$ et $\boldsymbol{B}$
$ A=\sqrt{(2 x-1)^{2}}=|2x-1|=-(2x-1)=1-2x$
Car : $x≤\frac{1}{2}$
C.à.d. : $2x-1≤0$
$ B=\sqrt{(4 y-3)^{2}}=|4 y-3|=4 y-3$
Car : $y≥\frac{3}{4}$
C.à.d. : $4 y-3≥0$
$3)$ Déterminer la valeur numérique du nombre $\boldsymbol{A}+\boldsymbol{B}$
On a: $x-2 y=5$
Donc :
$A+B=1-2 x+4 y-3=-2 x+4 y-2=-2(x-2 y)-2=-2 \times 5-2=-10-2=-12$
• Montrer que : $\left|\sqrt{\boldsymbol{x}}-\frac{1}{\sqrt{x}}\right|=\mathbf{1}$
On a : $\sqrt{x}+\frac{1}{\sqrt{x}}=\sqrt{5}$
Donc: $\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)^{2}=(\sqrt{5})^{2}$
$ (\sqrt{x})^{2}+2 \times \sqrt{x} \times \frac{1}{\sqrt{x}}+\left(\frac{1}{\sqrt{x}}\right)^{2}=5 $
$ x+2+\frac{1}{x}=5 $
$ x+\frac{1}{x}=3$
Alors:
$\left|\sqrt{x}-\frac{1}{\sqrt{x}}\right|=\left|\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2}\right|=\left|(\sqrt{x})^{2}-2 \times \sqrt{x} \times \frac{1}{\sqrt{x}}+\left(\frac{1}{\sqrt{x}}\right)^{2}\right|=\left|x-2+\frac{1}{x}\right|=\left|x+\frac{1}{x}-2\right|=|3-2|=|1|$
Donc: $\left|\sqrt{x}-\frac{1}{\sqrt{x}}\right|=1$
Modèle N°2
Questions indépendantes:$(1,5+2+1,5+1+1=7 pts)$
$1)$ On pose : $B=\sqrt{4+2 \sqrt{3}}+\sqrt{4-2 \sqrt{3}}$
Calculer $\boldsymbol{B}^{2}$ puis déduire une valeur de $\boldsymbol{B}$ plus simple.
$2)$ Soient $\boldsymbol{a}$ et $\boldsymbol{b}$ deux réels non nuls :
$a)$ Simplifier le nombre : $A=\frac{a b^{-2}\left(a^{-1} b\right)^{4}\left(a b^{-1}\right)^{2}}{a^{2} b\left(a^{2} b^{-1}\right)^{3} a^{-1} b}$
$b)$ Calculer $A$ pour : $a=10^{-\mathbf{2}}$ et $\boldsymbol{b}=\mathbf{1 0}^{\mathbf{- 3}}$.
$3)$ Factoriser les expressions suivantes:
$E=x^{3}-8+(x-2)(2 x-3) \text { et } F=(5 x-3)(x+1)-6 x+10 x^{2}+(3-5 x)^{2}$
$4)$ Résoudre dans $IR$ l’équation suivante : $4-x^{2}=(x+2)(2 x+5)$
$5)$ Donner l’écriture scientifique du nombre $\boldsymbol{G}$ tel que :
$G=15 \times 10^{2}+2 \times 10^{-2}-1,2 \times 10^{3}$
Exercice 1:$(2+2+1+1=6 pts)$
Soit $\boldsymbol{A B C}$ un triangle et $\boldsymbol{M}$ un point tel que :
$\overrightarrow{\boldsymbol{A M}}=\frac{2}{3} \overrightarrow{\boldsymbol{A B}}$
• $ N$ est le projeté de $\boldsymbol{M}$ sur $(A C)$ parallèlement à ( $B C)$
• $\boldsymbol{F}$ est le projeté de $N$ sur $(\boldsymbol{B C})$ parallèlement à $(\boldsymbol{A B})$
$1)$ Construire la figure.
$2)$ Montrer que $\overrightarrow{A N}=\frac{2}{3} \overrightarrow{A C}$ et $\overrightarrow{M N}=\frac{2}{3} \overrightarrow{B C}$
$3)$ Montrer que $\overrightarrow{\boldsymbol{C F}}=\frac{\mathbf{- 1}}{\mathbf{3}} \overrightarrow{\boldsymbol{B C}}$
$4)$ Déduire que : $\overrightarrow{M N}=\overrightarrow{B F}$
Exercice 2:$(1+1,5+1,5+1=6 pts)$
Soient $a$ et $b$ deux réels tels que : $a=1+\sqrt{4-\frac{3}{2} \sqrt{7}}$ et $b=1+\sqrt{4+\frac{3}{2} \sqrt{7}}$
$1)$ Vérifier que : $(3-\sqrt{7})^{2}=4\left(4-\frac{3}{2} \sqrt{7}\right)$ et $(3+\sqrt{7})^{2}=4\left(4+\frac{3}{2} \sqrt{7}\right)$
$2) $Montrer que : $\boldsymbol{a}+\boldsymbol{b}=\mathbf{5}$
$3)$ Montreque : $(a-1)(b-1)=\frac{1}{2}$
$4)$ En déduire la valeur du produit : $a b$
Exercice 3:$(2 pts)$
Montrer que : $\left(\frac{\sqrt{85}+1}{2}\right)^{3}-\left(\frac{\sqrt{85}-1}{2}\right)^{3}=64$
$1)$ On pose : $B=\sqrt{4+2 \sqrt{3}}+\sqrt{4-2 \sqrt{3}}$
$ B^{2}=(\sqrt{4+2 \sqrt{3}}+\sqrt{4-2 \sqrt{3}})^{2}$
$B^{2}=(\sqrt{4+2 \sqrt{3}})^{2}+2 \sqrt{4+2 \sqrt{3}} \times \sqrt{4-2 \sqrt{3}}+(\sqrt{4-2 \sqrt{3}})^{2} $
$ B^{2}=|4+2 \sqrt{3}|+2 \sqrt{(4+2 \sqrt{3})(4-2 \sqrt{3})}+|4-2 \sqrt{3}|$
$B^{2}=4+2 \sqrt{3}+2 \sqrt{\left(4^{2}-(2 \sqrt{3})^{2}\right)}+4-2 \sqrt{3} $
$ B^{2}=8+2 \sqrt{(16-12)}=8+2 \sqrt{4}=8+2 \times 2=12$
Alors : $B=\sqrt{12}=\sqrt{4 \times 3}=2 \sqrt{3}$
$2)$ Soient $\boldsymbol{a}$ et $\boldsymbol{b}$ deux réels non nuls :
a) Simplifier $A$ :
$A=\frac{a b^{-2}\left(a^{-1} b\right)^{4}\left(a b^{-1}\right)^{2}}{a^{2} b\left(a^{2} b^{-1}\right)^{3} a^{-1} b}$
$A=\frac{a b^{-2} \times a^{-4} b^{4} \times a^{2} b^{-2}}{a^{2} b \times a^{6} b^{-3} \times a^{-1} b}$
$A=\frac{a \times a^{-4} \times a^{2}}{a^{2} \times a^{6} \times a^{-1}} \times \frac{b^{-2} \times b^{4} \times b^{-2}}{b \times b^{-3} \times b}$
$A=\frac{a^{-1}}{a^{7}} \times \frac{b^{0}}{b^{-1}}$
$A=a^{-8} \times b$
b) Calculer A pour $\boldsymbol{a}=\mathbf{1 0}^{-\mathbf{2}}$ et $\boldsymbol{b}=\mathbf{1 0}^{-\mathbf{3}}$
$A=\left(10^{-2}\right)^{-8} \times\left(10^{-3}\right)=10^{16} \times 10^{-3}=10^{13}$.
$3)$ Factoriser les expressions suivantes:
$E =x^{3}-8+(x-2)(2 x-3)$
$E=(x-2)\left(x^{2}+2 x+4\right)+(x-2)(2 x-3) $
$E= (x-2)\left(x^{2}+2 x+4+2 x-3\right)$
$E=(x-2)\left(x^{2}+4 x+1\right) $
$F =(5 x-3)(x+1)-6 x+10 x^{2}+(3-5 x)^{2} $
$ F=-(3-5 x)(x+1)-2 x(3-5 x)+(3-5 x)(3-5 x) $
$ F=(3-5 x)(-(x+1)-2 x+(3-5 x)) $
$ F=(3-5 x)(-x-1-2 x+3-5 x) $
$ F=(3-5 x)(-8 x+2)$
$4)$ Résoudre dans $IR$ l’équation suivante : $4-x^{2}=(x+2)(2 x+5)$
$4-x^{2}=(x-2)(2 x-3)$
$(x-2)(x+2)=(x-2)(2 x-3)$
$(x-2)(x+2)-(x-2)(2 x-3)=0$
$(x-2)((x+2)-(2 x-3))=0$
$(x-2)(5-x)=0$
Donc $:(x-2)=0$ ou $(5-x)=0$
Alors l’équation admet deux solutions : $x=2$ et $x=5$
$5)$ Donner l’écriture scientifique du nombre $\boldsymbol{G}$ tel que :
$G=15 \times 10^{2}+2 \times 10^{-2}-1,2 \times 10^{3}=15 \times 10^{2}+0.0002 \times 10^{2}-12 \times 10^{2}$ $G=(15+0,0002-12) \times 10^{2}=3,0002 \times 10^{2}$
$1)$ Construire la figure.
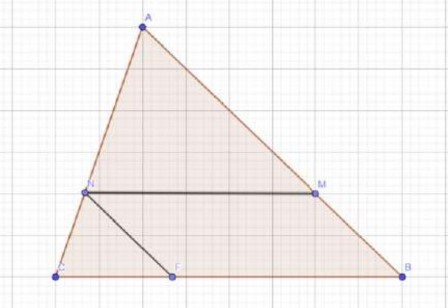
$2)$ Montrer que $\overrightarrow{A N}=\frac{2}{3} \overrightarrow{A C}$ et $\overrightarrow{M N}=\frac{2}{3} \overrightarrow{B C}$
• On a:
$N$ est le projeté de $M$ sur ( $\mathbf{A C}$ ) parallèlement à $(BC)$
$C$ est le projeté de $B$ sur $(AC)$ parallèlement à $(BC)$
$A$ est le projeté de $A$ sur $(AC)$ parallèlement à $(BC)$
Et $\quad \overrightarrow{A M}=\frac{2}{3} \overrightarrow{A B}$
Et puisque la projection conserve le coefficient de colinéarité
Donc: $\overrightarrow{A N}=\frac{2}{3} \overrightarrow{A C}$
• Dans le triangle $ABC$ les droites $(MN)//(BC)$
Alors d’après le théorème direct de Thalès :
$\frac{A M}{A B}=\frac{A N}{A C}=\frac{M N}{B C}=\frac{2}{3} \quad \operatorname{car}: A M=\frac{2}{3} A B$
Alors : $\frac{M N}{B C}=\frac{2}{3}$
Implique que : $\boldsymbol{M N}=\frac{2}{3} \boldsymbol{B C}$
Donc: $\quad \overrightarrow{M N}=\frac{2}{3} \overrightarrow{B C}$
$3)$ Montrer que $\overrightarrow{\boldsymbol{C F}}=\frac{\mathbf{- 1}}{\mathbf{3}} \overrightarrow{\boldsymbol{B C}}$
• On a:
$F$ est le projeté de $\mathbf{N}$ sur $(BC)$ parallèlement à $(AB)$
$B$ est le projeté de $\mathbf{A}$ sur $(BC)$ parallèlement à ( $\mathbf{A B}$ )
$C$ est le projeté de $C$ sur $(BC)$ parallèlement à $(AB)$
Et $\quad \overrightarrow{A N}=\frac{2}{3} \overrightarrow{A C}$
Et puisque la projection conserve le coefficient de colinéarité
Donc : $\overrightarrow{\boldsymbol{B F}}=\frac{2}{3} \overrightarrow{B C}$
Et: $\overrightarrow{B F}=\overrightarrow{\boldsymbol{BC}}+\overrightarrow{C F}=\frac{2}{3} \overrightarrow{B C}$
Alors : $\overrightarrow{\boldsymbol{BC}}+\overrightarrow{C F}=\frac{2}{3} \overrightarrow{B C}$
$\overrightarrow{C F}=\frac{2}{3} \overrightarrow{B C}-\overrightarrow{B C}$
Donc:
$\overrightarrow{C F}=-\frac{1}{3} \overrightarrow{B C}$
$4)$ Déduire que : $\overrightarrow{M N}=\overrightarrow{B F}$
On a : $\overrightarrow{M N}=\frac{2}{3} \overrightarrow{B C}$ et $\overrightarrow{B F}=\frac{2}{3} \overrightarrow{B C}$
Donc: $\overrightarrow{\boldsymbol{M N}}=\overrightarrow{\boldsymbol{B F}}$
$1)$ Vérifier que : $(3-\sqrt{7})^{2}=4\left(4-\frac{3}{2} \sqrt{7}\right)$ et $(3+\sqrt{7})^{2}=4\left(4+\frac{3}{2} \sqrt{7}\right)$
$(3-\sqrt{7})^{2} =9-6 \sqrt{7}+7=16-6 \sqrt{7}=4\left(4-\frac{3}{2} \sqrt{7}\right) $
$(3+\sqrt{7})^{2} =9+6 \sqrt{7}+7=16+6 \sqrt{7}=4\left(4+\frac{3}{2} \sqrt{7}\right)$
$2)$ Montrer que : $\boldsymbol{a}+\boldsymbol{b}=\mathbf{5}$
$a+b =1+\sqrt{4-\frac{3}{2} \sqrt{7}}+1+\sqrt{4+\frac{3}{2} \sqrt{7}}=2+\sqrt{\frac{(3-\sqrt{7})^{2}}{4}}+\sqrt{\frac{(3+\sqrt{7})^{2}}{4}}=2+\frac{|3-\sqrt{7}|}{2}+\frac{|3+\sqrt{7}|}{2} $
$ =2+\frac{3-\sqrt{7}}{2}+\frac{3+\sqrt{7}}{2}=2+\frac{3-\sqrt{7}+3+\sqrt{7}}{2}=2+\frac{6}{2}=2+3=5$
$3)$ Montrer que : $(a-1)(b-1)=\frac{1}{2}$
$a+b =1+\sqrt{4-\frac{3}{2} \sqrt{7}}+1+\sqrt{4+\frac{3}{2} \sqrt{7}}=2+\sqrt{\frac{(3-\sqrt{7})^{2}}{4}}+\sqrt{\frac{(3+\sqrt{7})^{2}}{4}}=2+\frac{|3-\sqrt{7}|}{2}+\frac{|3+\sqrt{7}|}{2} $
$=2+\frac{3-\sqrt{7}}{2}+\frac{3+\sqrt{7}}{2}=2+\frac{3-\sqrt{7}+3+\sqrt{7}}{2}=2+\frac{6}{2}=2+3=5$
$4)$ En déduire la valeur du produit : $a b$
On a: $(a-1)(b-1)=a b-a-b+1=a b-(a+b)+1=a b-5+1=a b-4$
Puisque: $(a-1)(b-1)=a b-4$
Alors : $a b-4=\frac{1}{2}$
Donc: $a b=\frac{1}{2}+4=\frac{9}{2}$
Montrer que : $\left(\frac{\sqrt{85}+1}{2}\right)^{3}-\left(\frac{\sqrt{85}-1}{2}\right)^{3}=64$
On sait que:
$(a)^{3}-(b)^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$
Alors :
$ \left(\frac{\sqrt{85}+1}{2}\right)^{3}-\left(\frac{\sqrt{85}-1}{2}\right)^{3}=\left(\left(\frac{\sqrt{85}+1}{2}\right)-\left(\frac{\sqrt{85}-1}{2}\right)\right)\left(\left(\frac{\sqrt{85}+1}{2}\right)^{2}+\left(\frac{\sqrt{85}+1}{2}\right)\left(\frac{\sqrt{85}-1}{2}\right)+\left(\frac{\sqrt{85}-1}{2}\right)^{2}\right) $
$\quad=\left(\frac{\sqrt{85}+1-\sqrt{85}+1}{2}\right)\left(\left(\frac{86+2 \sqrt{85}}{4}\right)+\left(\frac{85-1}{4}\right)+\left(\frac{86-2 \sqrt{85}}{4}\right)\right) $
$ \quad=\left(\frac{86+2 \sqrt{85}+84+86-2 \sqrt{85}}{4}\right) $
$ \quad=\left(\frac{256}{4}\right) $
$ \quad=64$
Modèle N°3
Exercice 1:$(8 pts)$
Soient $x \geq \frac{1}{2} ; y \leq 1$ et $x-y=3$.
Partie 1 : $(1,5+1+1,5 )$
$1)$ Déterminer la valeur du nombre $A$ tel que: $A=\sqrt{(2 x-1)^{2}}+\sqrt{(2 y-2)^{2}}$
$2)$ Montrer que: $\frac{1}{2} \leq x \leq 4$ et $-\frac{5}{2} \leq y \leq 1$.
$3)$ En déduire la simplification de l’écriture du nombre: $B=|x+y-5|+|x+y+2|$
Partie 2 : $(0,5+0,5+1,5+1,5)$
$1)$ Soient deux intervalles suivants : $I=]-\infty ; 3]$ et $J=[-5 ;+\infty[$
$a)$ Représenter les deux intervalles sur une droites graduée.
$b)$ Déterminer $I \cap J$ e $I \cup J$.
$2)$ Résoudre dans $\mathbb{R}$ :
$a)$ $|3 x+2|=|9 x+8|$
$b)$ $\left|5 x-\frac{1}{2}\right|>0$
Exercice 2:$(1+1,5+1,5+1,5+1,5=7 pts)$
$a$ et $b$ deux nombres réels tels que $|2 b-3| \leq 5$ et $5$ une approximation de $4 a-3$ par excès à $4$ prés.
$1)$ Montrer que $1 \leq a \leq 2$ et $-1 \leq b \leq 4$
$2)$ Simplifier le nombre $A=|a+b|+|a-2 b-4|$
$3)$ On pose: $x=\frac{6 a^{2}+b}{\sqrt{b+5}+2}$
$a)$ Montrer que : $1 \leq x \leq 7$.
$b)$ En déduire que $4$ valeur approchée de $x$ à $3$ près
Exercice 3:$(1+1,5+1,5+1,5+1,5=7 pts)$
On considère les points $A(4 ;-5) ; B(1 ; 4)$ et $C(9 ;-6)$ et la droite $(D)$ définie par la représentation paramétrique: $\left\{\begin{array}{c}x=9-8 t \\ y=-6+10 t\end{array} /(t \in \mathbb{R})\right.$
$1)$$a)$ Vérifier que les points $B$ et $C$ appartiennent à la droite ( $D$ ).
$b)$ Montrer que $5 x+4 y-21=0$ est une équation cartésienne de la droite ( $D$ ).
$2)$ Soit ( $\Delta$ ) la droite passant par $A$ et dirigée par le vecteur $\overrightarrow{O B}$.
• Montrer que $4 x-y-21=0$ est une équation cartésienne de la droite ( $\Delta$ ).
$3)$ Déterminer le couple de coordonnées du point $I$ d’intersection des $(D)$ et ( $\Delta$ ).
$4) $Étudier la position relative des droits $(\Delta)$ et $(L)$ de l’équation: $(L): x+y=0$.
Soient $x \geq \frac{1}{2} ; y \leq 1$ et $x-y=3$.
Partie 1 :
$1)$ Déterminer la valeur du nombre $A$ tel que: $A=\sqrt{(2 x-1)^{2}}+\sqrt{(2 y-2)^{2}}$
$A=\sqrt{(2 x-1)^{2}}+\sqrt{(2 y-2)^{2}}$
$A=|2 x-1|+|2 y-2|$
On a : $x \geq \frac{1}{2}$ donc : $2 x-1 \geq 0$
Et : $y \leq 1$ donc : $2 y-2 \leq 0$
Alors: $A=2 x-1+2-2 y$
$ A=2 x-2 y+1 $
$ A=2(x-y)+1 $
$ A=2 \times 3+1 $
$ A=7$
$2)$ Montrer que: $\frac{1}{2} \leq x \leq 4$ et $-\frac{5}{2} \leq y \leq 1$.
On a : $\frac{1}{2} \leq x$ et $x-y=3 \Rightarrow x=y+3$
Et on sait que : $y \leq 1 \Rightarrow y+3 \leq 4 \Rightarrow x \leq 4$
Alors: $\frac{1}{2} \leq x \leq 4$
On a : $\frac{1}{2} \leq x$ et $\frac{1}{2} \leq y+3 \Rightarrow \frac{1}{2}-3 \leq y \Rightarrow-\frac{5}{2} \leq y$
Donc: $-\frac{5}{2} \leq y \leq 1$
$3)$ En déduire la simplification de l’écriture du nombre: $B=|x+y-5|+|x+y+2|$
On a : $\frac{1}{2} \leq x \leq 4$ et $-\frac{5}{2} \leq y \leq 1$
Alors : $-2 \leq x+y \leq 5$
Donc : $-\mathbf{7} \leq \boldsymbol{x}+\boldsymbol{y}-\mathbf{5} \leq \mathbf{0}$ (intervalle négatif)
Et : $\mathbf{0} \leq \boldsymbol{x}+\boldsymbol{y}+\mathbf{2} \leq \mathbf{7}$ (intervalle positif)
Par conséquent : $B=-\boldsymbol{x}-\boldsymbol{y}+\mathbf{5}+\boldsymbol{x}+\boldsymbol{y}+\mathbf{2}$
Donc : $\boldsymbol{B}=\mathbf{7}$
Partie 2 : $(0,5+0,5+1,5+1,5)$
$1)$ Soient deux intervalles suivants : $I=]-\infty ; 3]$ et $J=[-5 ;+\infty[$
$a)$ Représenter les deux intervalles sur une droites graduée.

$b)$ Déterminer $I \cap J$ e $I \cup J$.
$I \cap J=[-5 ; 3] \quad ; \quad I \cup J=]-\infty ;+\infty[$
$2)$ Résoudre dans $\mathbb{R}$ :
$a)$ $|3 x+2|=|9 x+8|$
1er cas: $\quad \mathbf{3 x}+\mathbf{2}=\mathbf{9 x}+\mathbf{8}$
$3 x-9 x=8-2$
$-6 x=6$
$x=-1$
2ème cas: $3 x+2=-(9 x+8) $
$ 3 x+9 x=-8-2 $
$ 12 x=-10$
$ x=\frac{-10}{12}=\frac{-5}{6}$
Donc : $S={-1;\frac{-5}{6}}$
$b)$ $\left|5 x-\frac{1}{2}\right|>0$
$5 x-\frac{1}{2}>0$ ou $-\left(5 x-\frac{1}{2}\right)>0$
$5 x>\frac{1}{2} \quad ou \quad-5 x>-\frac{1}{2}$
$x>\frac{1}{10} \quad$ ou $\quad x<\frac{1}{10}$
$S=]-\infty ; \frac{1}{10}[\cup] \frac{1}{10} ;+\infty[$
$1)$ Montrer que $1 \leq a \leq 2$ et $-1 \leq b \leq 4$
On a $5$ une approximation de $4 a-3$ par excès à $4$ prés, c’est-à-dire que :
$1 \leq 4 a-3 \leq 5$
$ 4 \leq 4 a \leq 8 $
$ 1 \leq a \leq 2$
On a : $|2 b-3| \leq 5$
C’est-à-dire que : $-5 \leq 2 b-3 \leq 5$
$-2 \leq 2 b \leq 8 $
$-1 \leq b \leq 4$
$2)$ Simplifier le nombre $A=|a+b|+|a-2 b-4|$
On a : $1 \leq a \leq 2$ et $-1 \leq b \leq 4$
Alors : $0 \leq a+b \leq 6 \quad$ donc : $|a+b|=a+b$
et $-8 \leq-2 b \leq 2 \Rightarrow-7 \leq a-2 b \leq 4 \quad \Rightarrow-11 \leq a-2 b-4 \leq 0$
Donc: $|a-2 b-4|=-(a-2 b-4)$
$A=|a+b|+|a-2 b-4|=a+b-a+2 b+4=3 b+4$
$3)$ On pose: $x=\frac{6 a^{2}+b}{\sqrt{b+5}+2}$
$a)$ Montrer que : $1 \leq x \leq 7$.
On a : $1 \leq a \leq 2$ et $-1 \leq b \leq 4$
$1 \leq a^{2} \leq 4 \Rightarrow 6 \leq 6 a^{2} \leq 24 \Rightarrow 5 \leq 6 a^{2}+b \leq 28$
Et : $-1 \leq b \leq 4 \Rightarrow 4 \leq b+5 \leq 9 \Rightarrow 2 \leq \sqrt{b+5} \leq 3 \Rightarrow 4 \leq \sqrt{b+5}+2 \leq 5$
Alors: $\frac{5}{5} \leq \frac{6 a^{2}+b}{\sqrt{b+5}+2} \leq \frac{28}{4}$
Donc : $1 \leq \frac{6 a^{2}+b}{\sqrt{b+5}+2} \leq 7$
$b)$ En déduire que $4$ valeur approchée de $x$ à $3$ près
On a : $1 \leq x \leq 7 \Rightarrow-3 \leq x-4 \leq 3 \quad \Rightarrow|x-4| \leq 3$
Donc $4$ est une valeur approchée de $x$ à $3$ près.
On considère les points $A(4 ;-5) ; B(1 ; 4)$ et $C(9 ;-6)$ et la droite $(D)$ définie par la représentation paramétrique: $\left\{\begin{array}{c}x=9-8 t \\ y=-6+10 t\end{array} /(t \in \mathbb{R})\right.$
$1)$
$a)$ Vérifier que les points $B$ et $C$ appartiennent à la droite ( $D$ ).
$\left\{\begin{array}{l}x_{A}=9-8 t \\ y_{A}=-6+10 t\end{array} \Rightarrow\left\{\begin{array}{c}4=9-8 t \\ -5=-6+10 t\end{array} \Rightarrow\left\{\begin{array}{c}4-9=-8 t \\ -5+6=10 t\end{array} \Rightarrow\left\{\begin{array}{c}-5=-8 t \\ 1=10 t\end{array} \Rightarrow\left\{\begin{array}{l}t=\frac{5}{8} \\ t=\frac{1}{10}\end{array}\right.\right.\right.\right.\right.$
Donc: $A \notin(D)$
$\left\{\begin{array}{l}x_{B}=9-8 t \\ y_{B}=-6+10 t\end{array} \Rightarrow\left\{\begin{array}{l}1=9-8 t \\ 4=-6+10 t\end{array} \Rightarrow\left\{\begin{array}{c}1-9=-8 t \\ 4+6=10 t\end{array} \Rightarrow\left\{\begin{array}{c}-8=-8 t \\ 10=10 t\end{array} \Rightarrow\left\{\begin{array}{l}t=1 \\ t=1\end{array}\right.\right.\right.\right.\right.$
Donc: $B \in(D)$
$b)$ Montrer que $5 x+4 y-21=0$ est une équation cartésienne de la droite ( $D$ ).
D’après la représentation paramétrique $\overrightarrow{\boldsymbol{u}}(-8 ; 10)$ est le vecteur directeur de la droite (D).
$10 x+8 y+c=0$
On a : $B \in(D)$
Alors: $10 x_{B}+8 y_{B}+c=0 \Rightarrow 10 \times 1+8 \times 4+c=0 \Rightarrow 42+c=0 \Rightarrow c=-42$
Donc :
$10 x+8 y-42=2(5 x+4 y-21)=0 $
$5 x+4 y-21=0$
$2)$ Soit ( $\Delta$ ) la droite passant par $A$ et dirigée par le vecteur $\overrightarrow{O B}$.
On a $A \in(\Delta)$ et $\overrightarrow{O B}(1 ; 4)$ vecteur directeur de la droite ( $\Delta$ ), donc: $\quad \boldsymbol{x} \boldsymbol{x}-\boldsymbol{y}+\boldsymbol{c}=\mathbf{0}$
Alors : $4 x_{A}-y_{A}+c=0 \Rightarrow 4 \times 4+5+c=0 \Rightarrow 21+c=0 \Rightarrow c=-21$
$4 x-y-21=0$
$3)$ Déterminer le couple de coordonnées du point $I$ d’intersection des $(D)$ et ( $\Delta$ ).
$\left\{\begin{array}{l}5 x + 4 y – 2 1 = 0 \\ 4 x – y – 2 1 = 0 \end{array} \Rightarrow\left\{\begin{array}{l}5 x + 4 y = 2 1 \\4 x – y = 2 1\end{array} \Rightarrow\left\{\begin{array}{c}5 x+4 y=21 \\ 16 x-4 y=84\end{array}\right.\right.\right.$
$5 x+16 x+4 y-4 y=21+84 $
$21 x=105 $
$x=5$
On remplace $x$ dans : $5 x+4 y=21$
$25+4 y=21 $
$4 y=-4 $
$y=-1$
Par conséquent : $I(5 ;-1)$
$4)$ Étudier la position relative des droits $(\Delta)$ et $(L)$ de l’équation: $(L): x+y=0$.
( $\Delta$ ): $4 x-y-21=0$
$(L): \boldsymbol{x}+\boldsymbol{y}=\mathbf{0}$
On a : $4 \times 1-1 \times(-1)=4+5=9 \neq 0$
Donc les droites sont sécantes.
Devoirs Corrigés Maths N°2 S1 Tronc commun
