ℵ Devoir N°2 Modèle 1
ℵ Devoir N°2 Modèle 2
ℵ Devoir N°2 Modèle 3
ℵ Devoir N°2 Modèle 4
ℵ Devoir N°2 Modèle 5
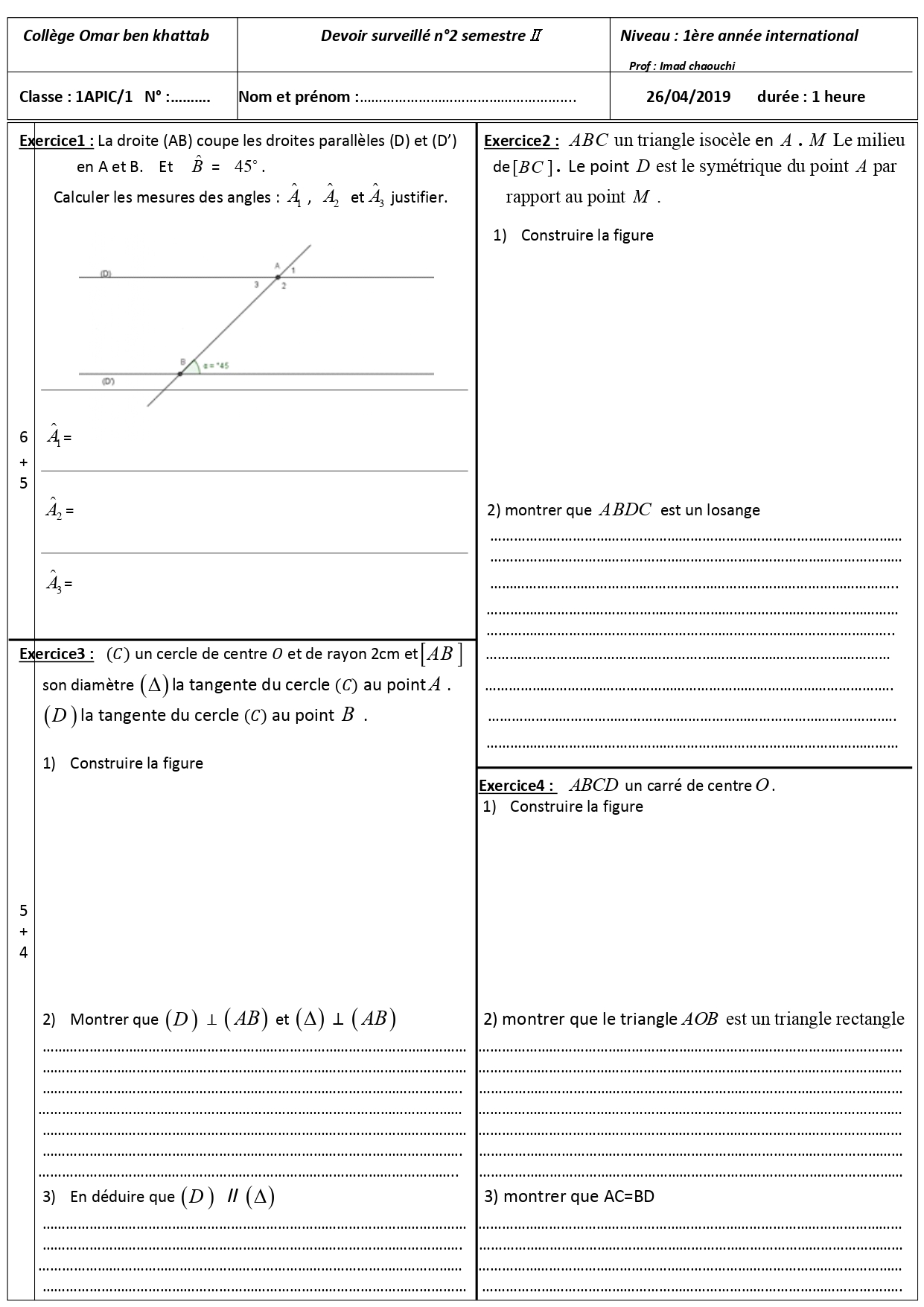
1) Construire la figure
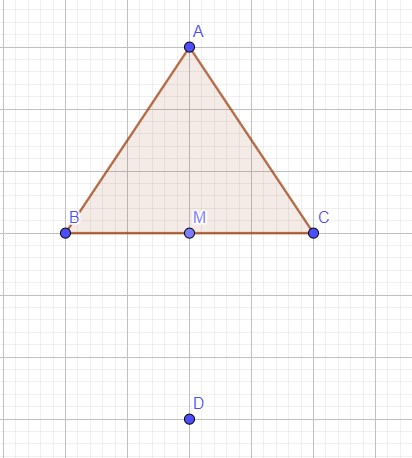
2) montrer que ABDC est un losange
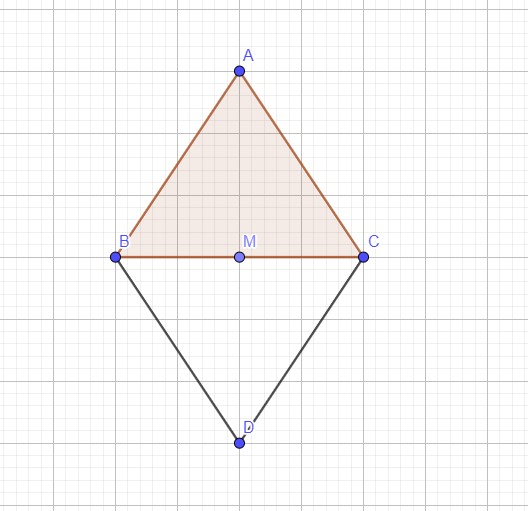
Le triangle ABC est isocéle en A (AB=AC)
En plus le point D est le symétrique de A par rapport au point M,donc le triangle BDC est le symétrique du triangle ABC par rapport au point M.
Alors les quartes cotés sont de même longueur, et ses diagonales perpendiculaires qui se coupent en leur milieu.
Donc le quadrilatère est un losange.
1) Construire la figure
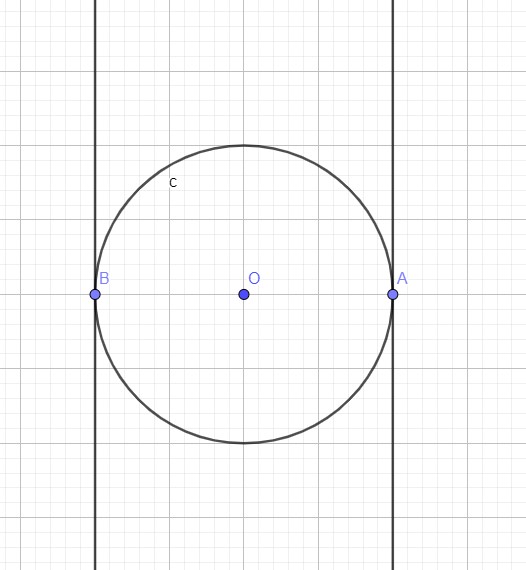
2) Montrer que (D ) ⊥ ( AB ) et (Δ) ⊥ ( AB )
(D ) la tangente du cercle (C) au point B ,alors (D)⊥ (AB)
(Δ) la tangente du cercle (C) au point A , alors (Δ)⊥ (AB)
3) En déduire que (Δ ) // (D)
On a : (D)⊥ (AB) et (Δ)⊥ (AB)
Alors :
(Δ)// (D)
1) Construire la figure
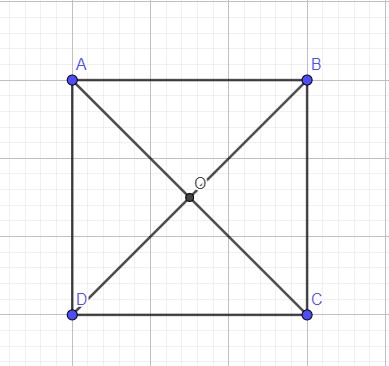
2) montrer que le triangle AOB est un triangle rectangle
ABCD est un carrée , donc ses diagonales sont perpendiculaires au point O.
Puisque l’angle AOB est droit,alors le triangle AOB est un triangle rectangle en O.
3) montrer que AC=BD
Puisque ABCD est un carrée , donc ses diagonales sont de même longueur.
AC = BD
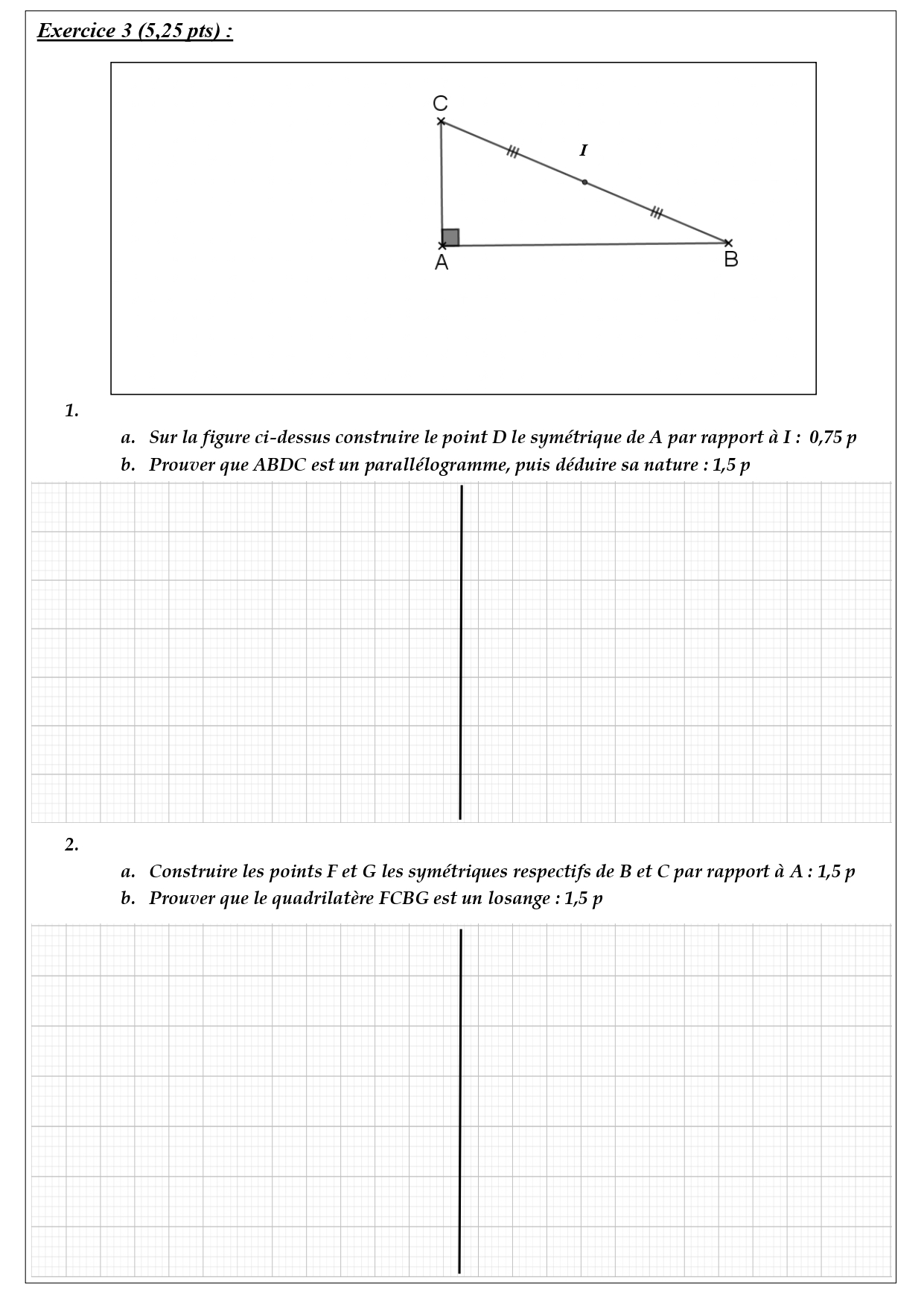
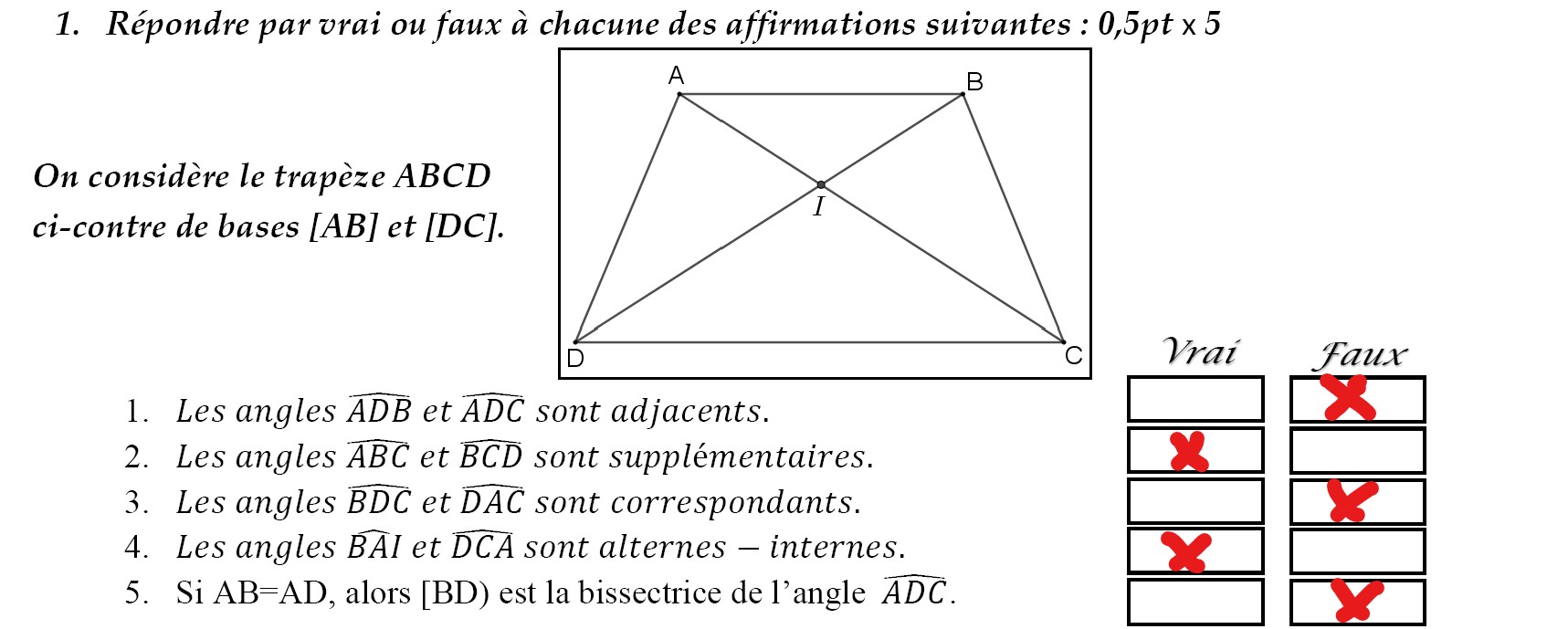
1.
a. Sur la figure ci-dessus construire le point D le symétrique de A par rapport à I : 0,75 p
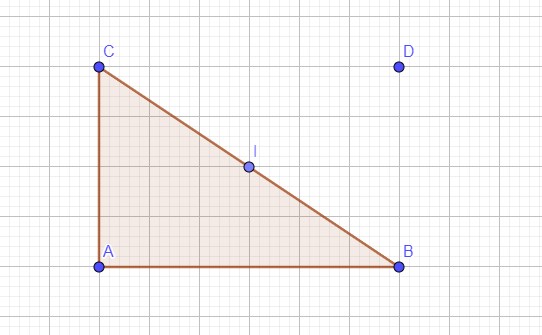
b. Prouver que ABDC est un parallélogramme, puis déduire sa nature : 1,5 p
• I est le milieu du segment [BC], donc le point C est le symétrique de B par rapport à I.
Aussi , le point D est le symétrique de A par rapport à I.
donc un parallélogramme a un centre de symétrie qui est le point d’intersection de ses diagonales.
• La nature de ce parallélogramme est rectangle.
2.
a. Construire les points F et G les symétriques respectifs de B et C par rapport à A : 1,5 p
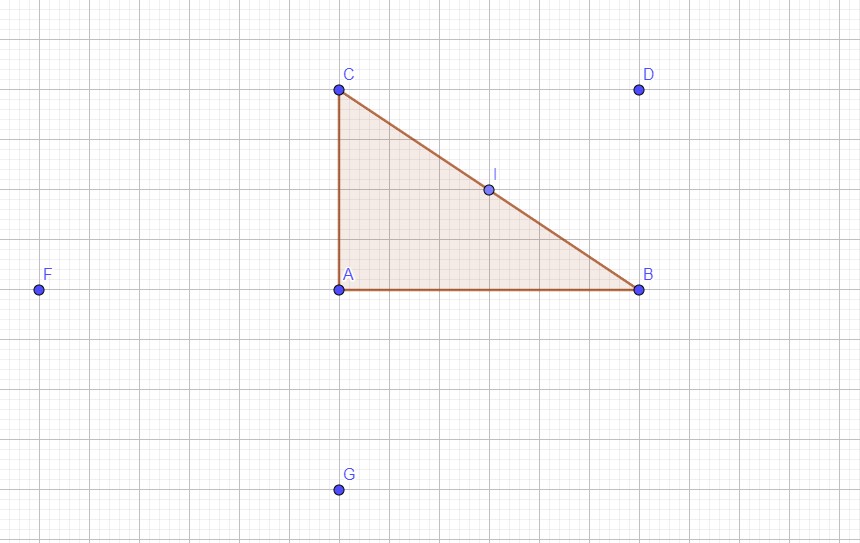
b. Prouver que le quadrilatère FCBG est un losange : 1,5 p
F et G les symétriques respectifs de B et C par rapport à A.
Alors dans le quadrilatère FCBG les quartes cotés sont de même longueur, et ses diagonales perpendiculaires qui se coupent en leur milieu.
Donc le quadrilatère FCBG est un losange.
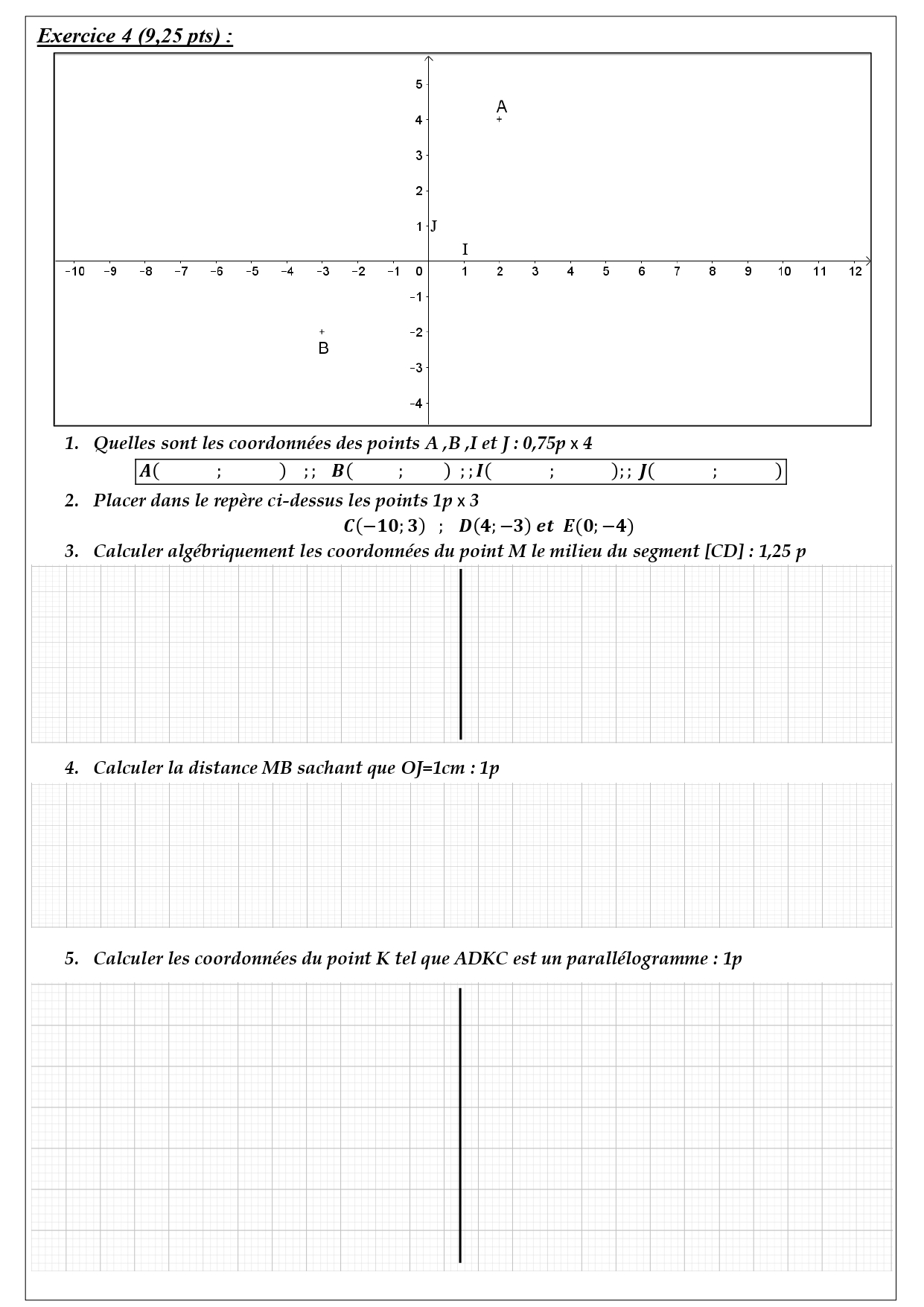
1. Quelles sont les coordonnées des points A ,B ,I et J : 0,75p x 4
A(2;4) ; B(-3 ;-2) ; I(1;0) ; J(0;1)
2.Placer dans le repère ci-dessus les points 1p x 3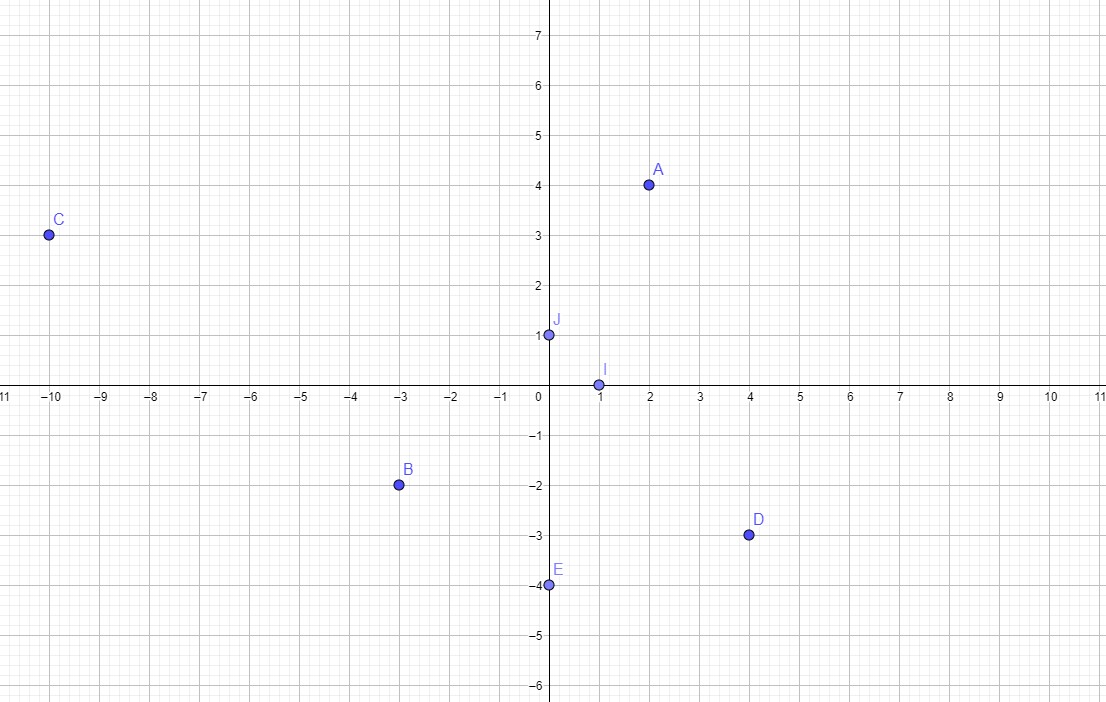
NB: les questions 3,4 et 5 appartiennent au programme de la 3ème année collège
3. Calculer algébriquement les coordonnées du point M le milieu du segment [CD] : 1,25 p
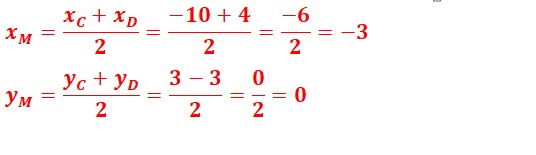
4. Calculer la distance MB sachant que OJ=1cm : 1p
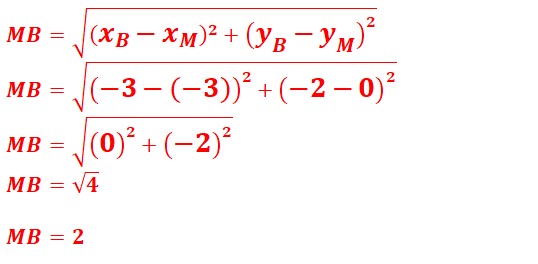
5. Calculer les coordonnées du point K tel que ADKC est un parallélogramme : 1p
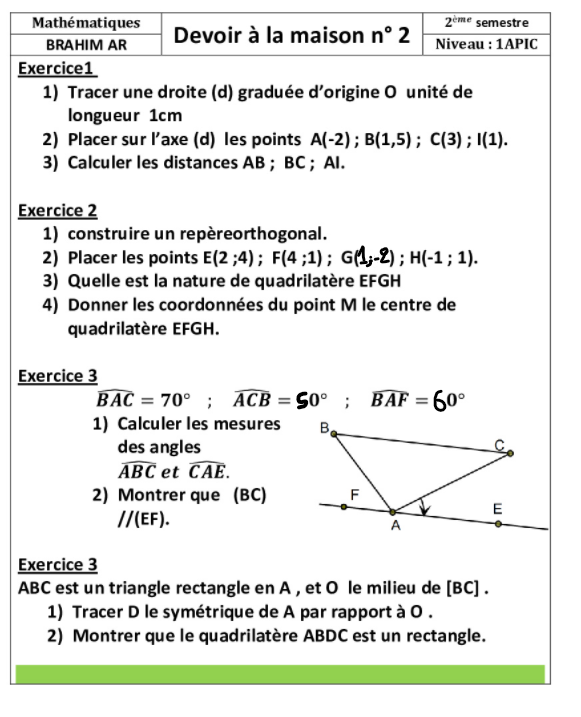
1) Tracer une droite (d) graduée d’origine O unité de longueur 1cm

2) Placer sur l’axe (d) les points A(-2) ; B(1,5) ; C(3) ; I(1).

3) Calculer les distances AB ; BC ; AI.
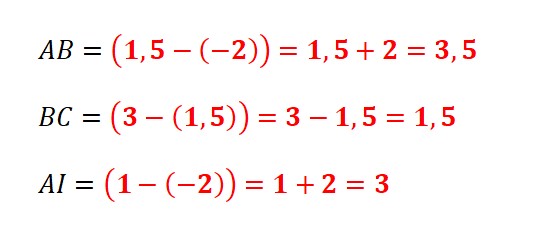
1) Construire un repère orthogonal.
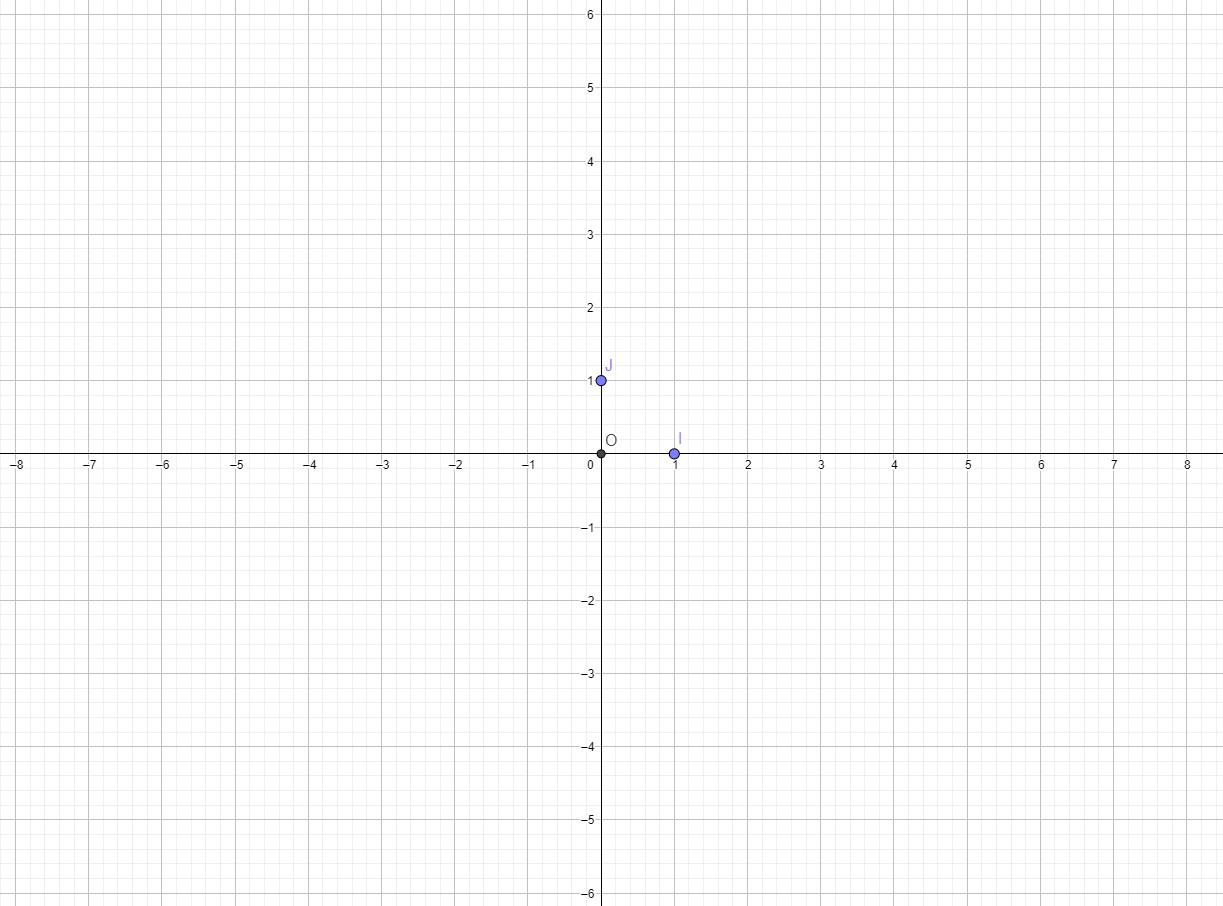
2) Placer les points E(2 ;4) ; F(4 ;1) ; G(1 ;-2) ; H(-1 ; 1).
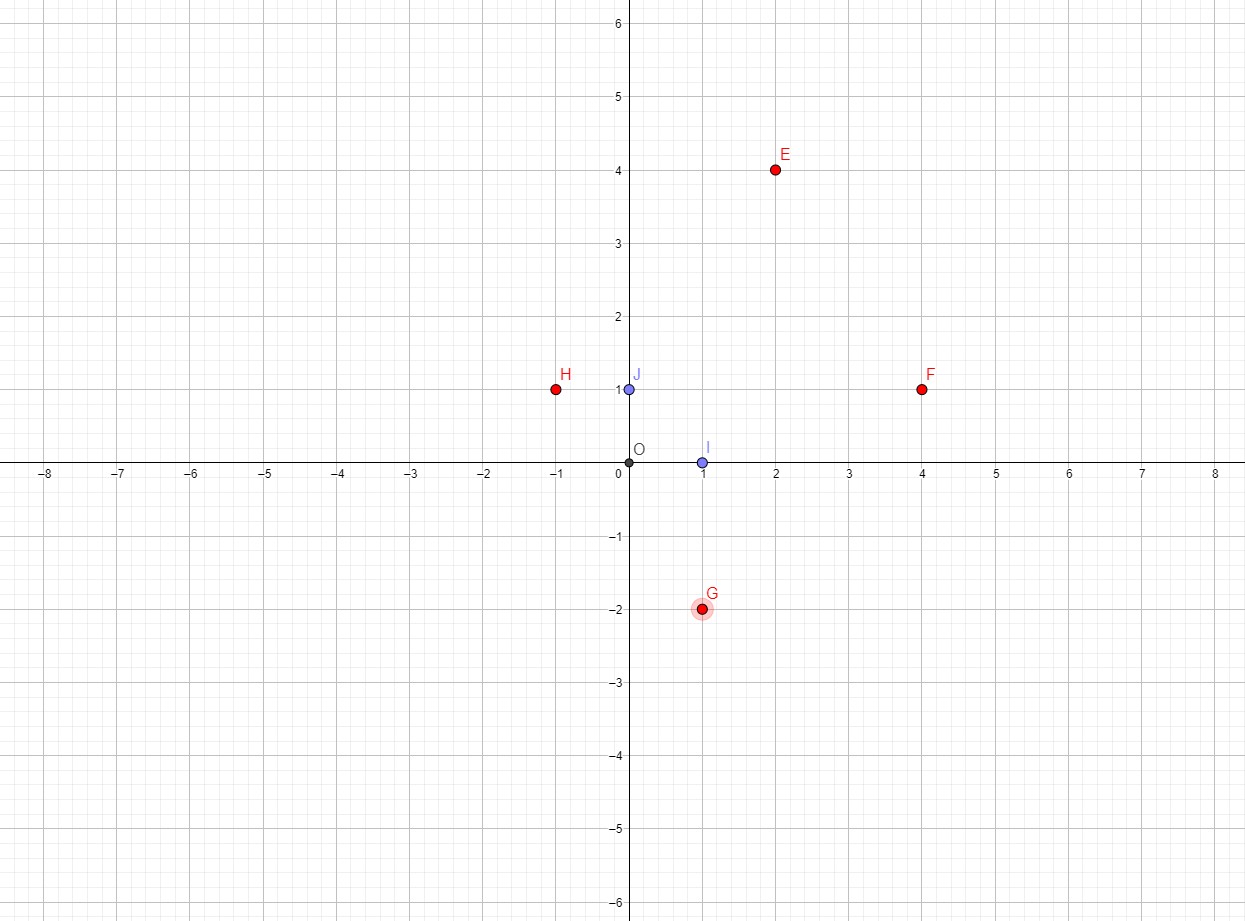
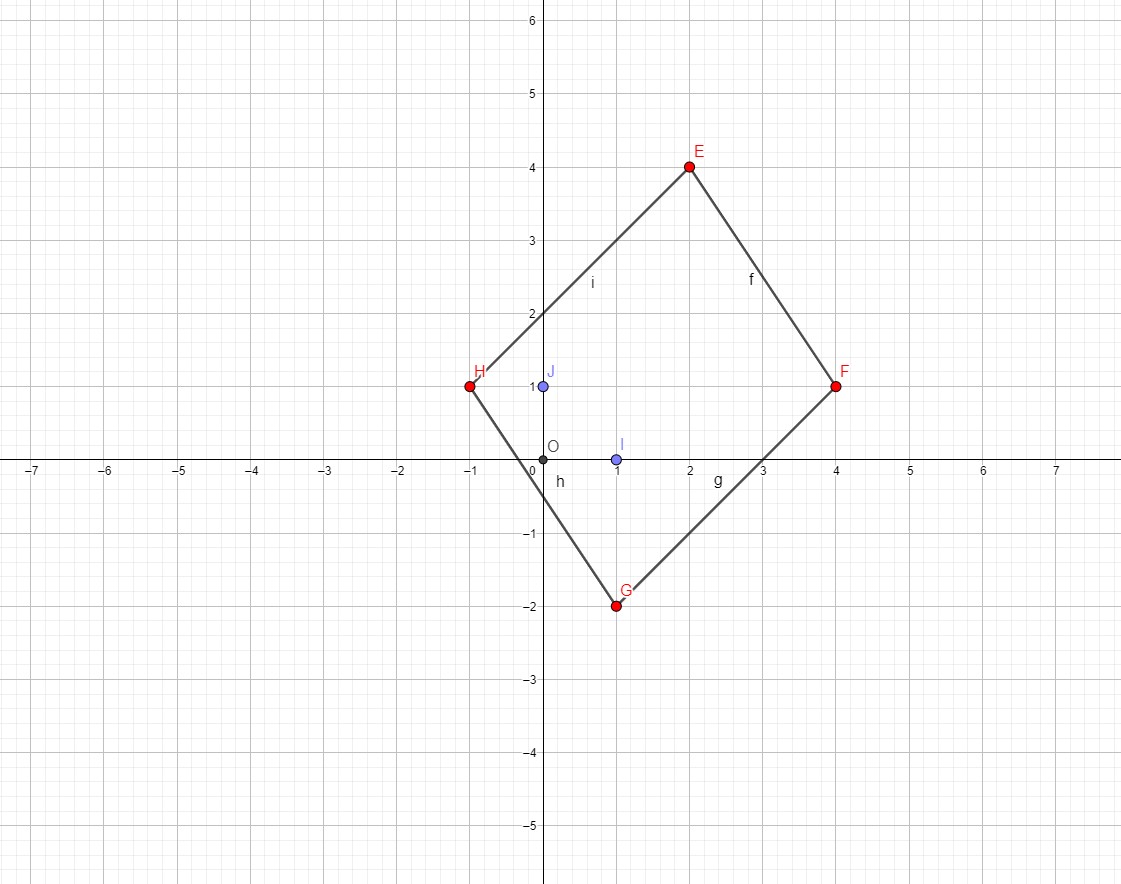
3) Quelle est la nature de quadrilatère EFGH
Un parallélogramme
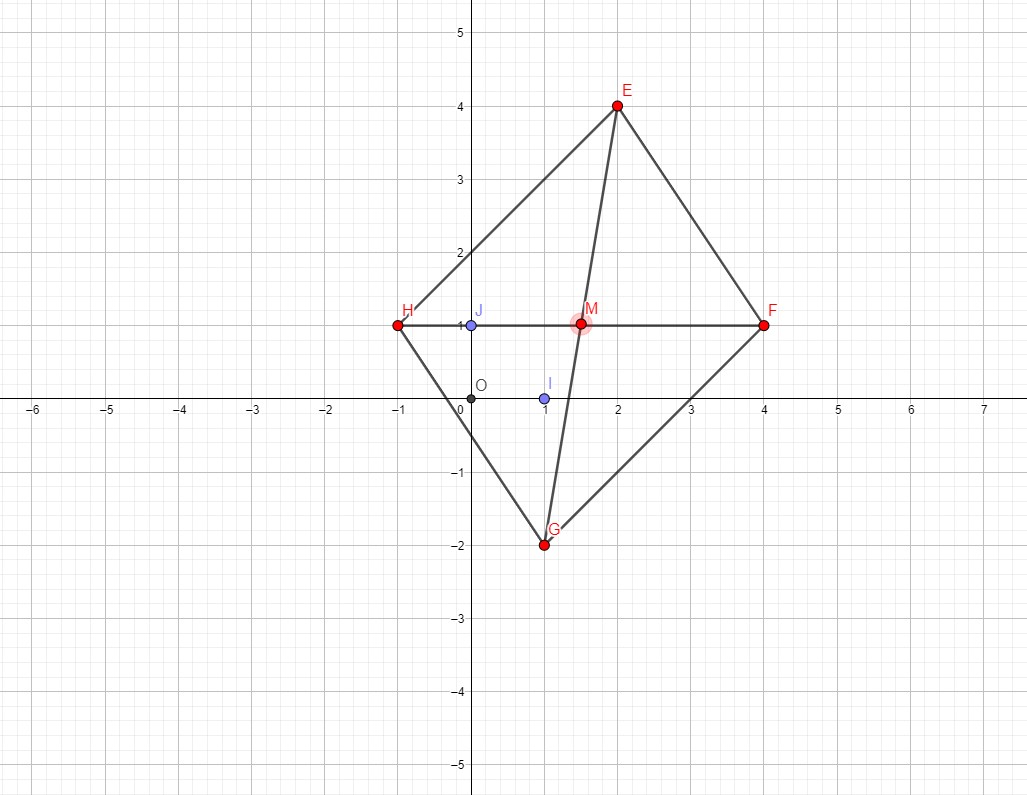
4) Donner les coordonnées du point M le centre de quadrilatère EFGH.
M(1,5 ; 1)
ABC est un triangle rectangle en A , et O le milieu de [BC] .
1) Tracer D le symétrique de A par rapport à O .

2) Déterminer la nature du quadrilatère ABDC .
O le milieu de [BC],alors OB=OC.
En plus D est le symétrique de A par rapport à O.
Puisque les diagonales [AD] et [BC] ont le même milieu
Alors ABDC est un parallélogramme