ℵ Devoir N°2 Modèle 1
ℵ Devoir N°2 Modèle 2
ℵ Devoir N°2 Modèle 3
ℵ Devoir N°2 Modèle 4
ℵ Devoir N°2 Modèle 5
Résoudre les équations suivantes :
Trois frères ont respectivement 48 , 26 et 14 ans , Dans combien d’années l’âge de l’aîné sera-t-il égal à la somme
des âges des deux autres ?
1. Le choix de l’inconnue :
Soit x le nombre d’années cherché
2. La mise en équation :
48+x = 26+x +14+x
3. Résolution de l’équation :
48+x = 26+x +14+x
48+x=40+2x
x – 2x = 40 – 48
-x = -8
x = 8
4. conclusion :
Dans 8 ans l’age de l’ainé sera égale à la somme des plus jeunes
Simplifier :
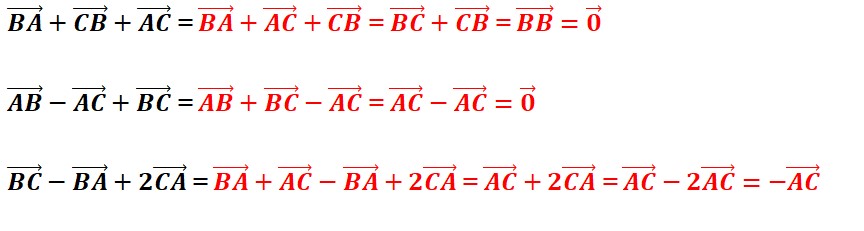
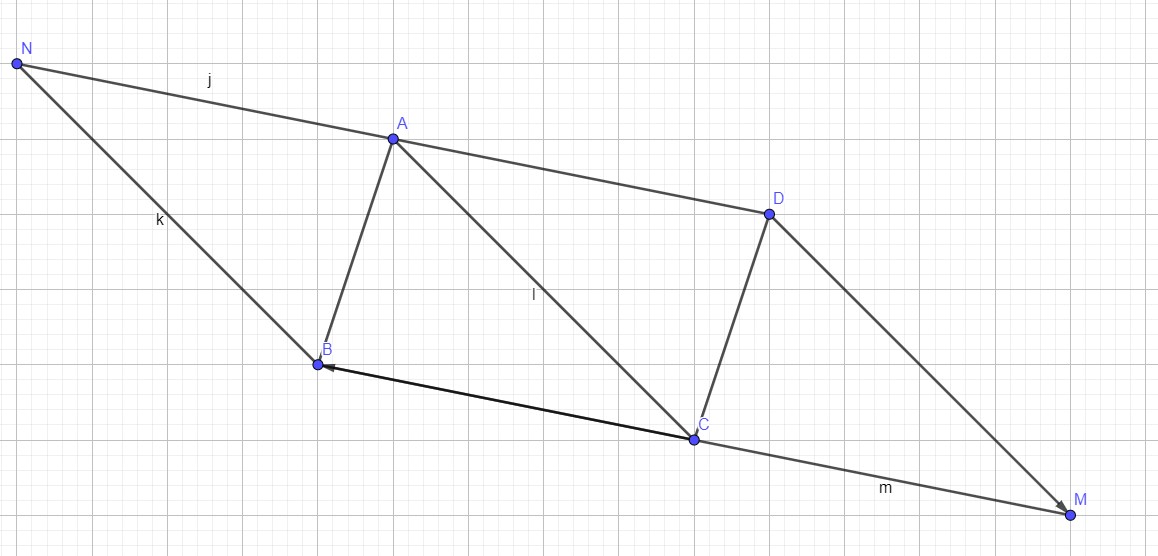
ABC est un triangle
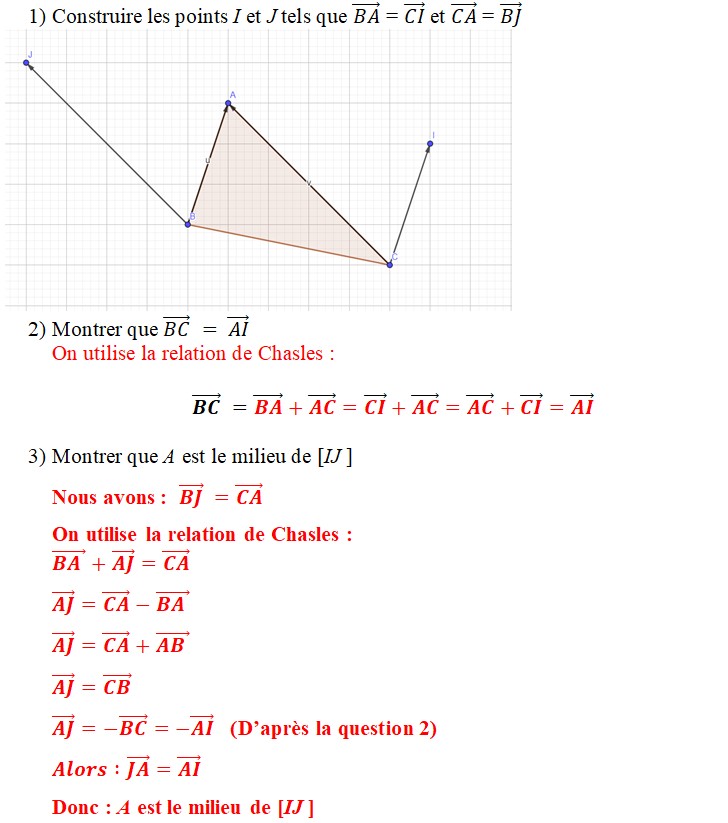
ABCD est un parallélogramme
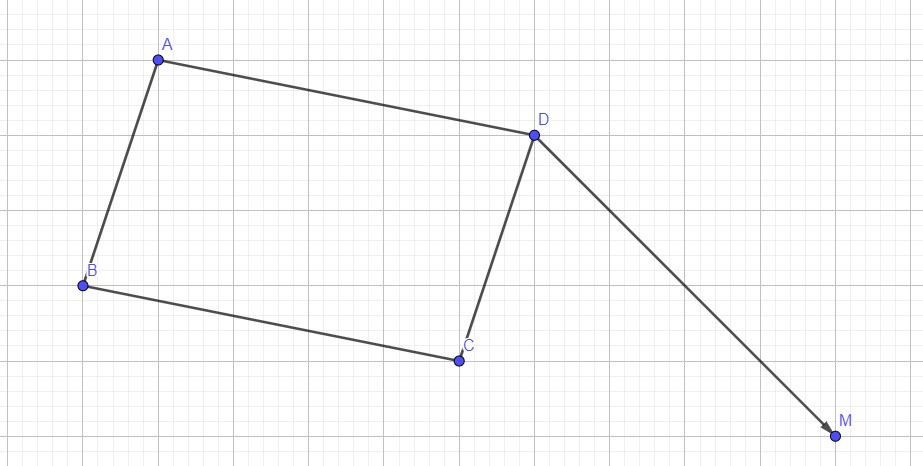
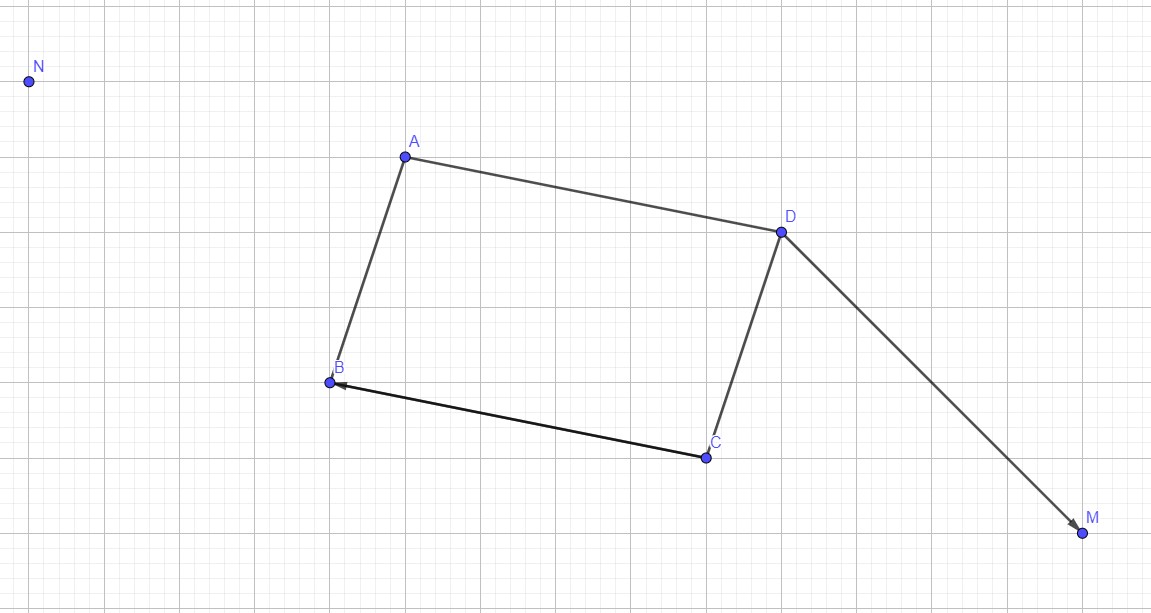
1) Construire le point M tel que:
2) Construire le point N l’image de A par la translation de vecteur:
3) Montrer que B est l’image de N par la translation de vecteur:

Soit PQR un triangle rectangle en P tel que : PQ = 4cm
1) Construire le point S tel que : 𝐏𝐒⃗⃗⃗⃗⃗ = 𝐏𝐐⃗⃗⃗⃗⃗ + 𝐏𝐑⃗⃗⃗⃗⃗
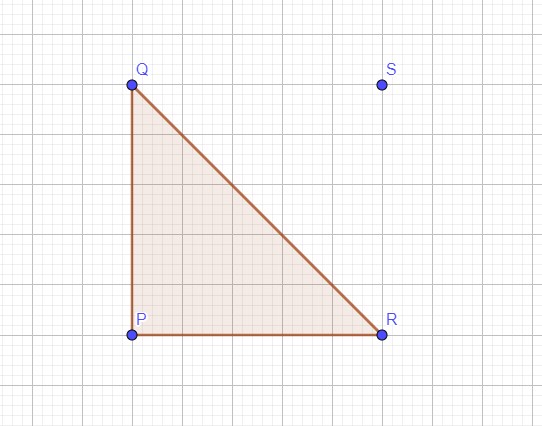
2) Quelle est la nature du quadrilatère PQSR.
Le quadrilatère PQSR il a quatre côtés de même longueur avec quatre angles droits
3) Construire le point M l’image de R par la translation 𝐐𝐏⃗⃗⃗⃗⃗ .
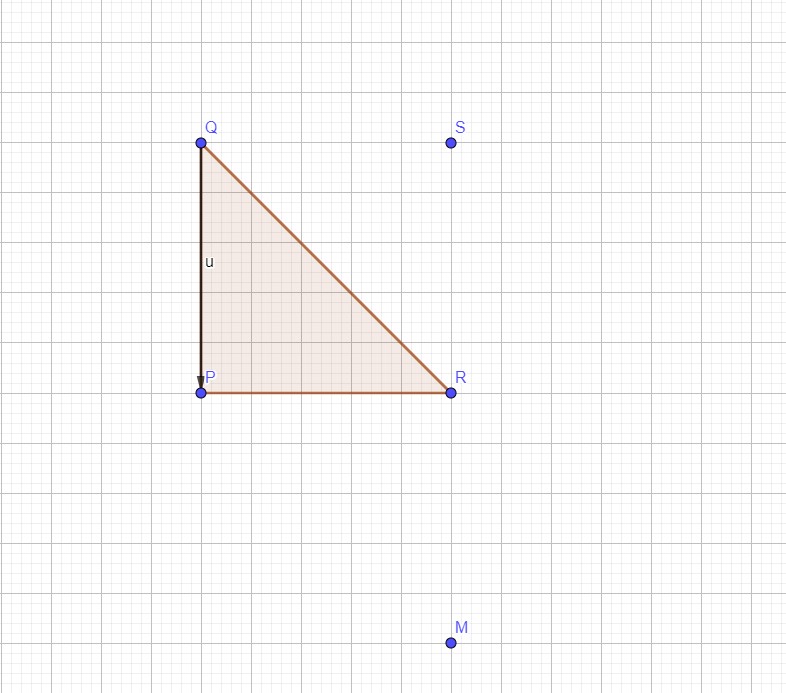
4) Montrer que R est le milieu de [MS].
On considère les points H ,G , F et E dans un plan :
• Simplifier :
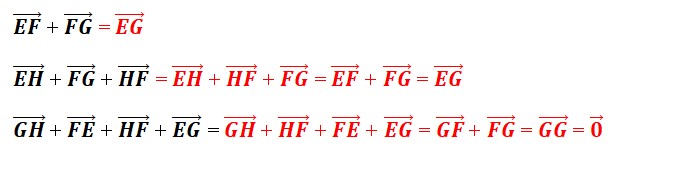
Résoudre les équations suivantes :