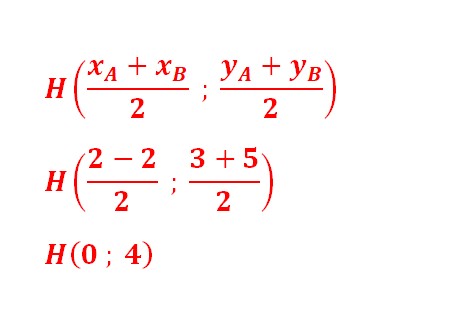Devoirs Corrigés Maths N°2 S2 3AC
Modèle N°1
Exercice 1: $(7 pts)$
Dans le plan muni d’un repère orthonormé ( $\mathrm{O}, \mathrm{I}, \mathrm{J}$ ), on considère les points suivants : $A(4,3)$ et $B(-2,5)$.
$1)$ Déterminer les coordonnées des vecteurs: $\overrightarrow{A B}$ et $\overrightarrow{A I}$. $(2 pts)$
$2)$ Calculer les distances : $AB$ et $BI$. $(2 pts)$
$3)$ Déterminer les coordonnées du point $M$ milieu de $[A B]$. $(1 pt)$
$4)$ Déterminer les coordonnées du point $N$ image du point $M$ par la translation de vecteur $\overrightarrow{A B}$. $(2 pts)$
Exercice 2:$(9 pts)$
Dans le plan muni d’un repère orthonormé ( $\mathrm{O}, \mathrm{I}, \mathrm{J}$ ), on considère les points suivants :
$A(0,2)$ et $B(4,4)$.
$1)$ Déterminer l’équation réduite de la droite $(A B)$. $(1 pt)$
$2)$ Déterminer parmi les points suivants ceux qui appartiennent à la droite ( $A B$ ): $R(0,-2)$ et $S(2,3)$. $(2 pts)$
$3)$ Déterminer l’équation réduite de la droite $(D)$ image de la droite $(AB)$ par la translation du vecteur $\overrightarrow{A B}$ et qui passe par le point $M(0,3)$. $(1,5 pts)$
$4)$ Déterminer l’équation réduite de la droite $(\Delta)$ la médiatrice du segment $[A B]$. $(1,5 pts)$
$5)$ Déterminer le point d’intersection de la droite $(D)$ avec l’axe des abscisses. $(1 pt)$
$6)$ Tracer les droites $(D)$ et $(\Delta)$ dans un repère orthonormé. $(2 pts)$
Exercice 3:$(4 pts)$
$1)$ Résoudre le système suivant: $\left\{\begin{array}{l}x-y=20 \\ x+y=130\end{array}\right.$ $ \quad (2 pts)$
$2)$ Hamza a payé $130 Dh$ pour l’achat de légumes et fruits. $(2 pts)$
Sachant que le prix des achats de légumes dépasse celui des fruits de $20 Dh$ .
Déterminer le prix payé pour l’achat des légumes et le prix payé pour l’achat des fruits.
$1)$
• $\overrightarrow{A B}\left(x_{B}-x_{A} ; y_{B}-y_{A}\right)$
$\overrightarrow{A B}(-2-4 ; 5-3)$
$\overrightarrow{A B}(-6 ; 2)$
• $\overrightarrow{A I}\left(x_{I}-x_{A} ; y_{I}-y_{A}\right)$
Les coordonnées de $I(1 ; 0)$
$\overrightarrow{A I}(1-4 ; 0-3)$
$\overrightarrow{A I}(-3 ;-3)$
$2)$
• $A B=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}$
$A B=\sqrt{(-6)^{2}+(2)^{2}}$
$A B=\sqrt{36+4}$
$A B=\sqrt{40}$
• $B I=\sqrt{\left(x_{I}-x_{B}\right)^{2}+\left(y_{I}-y_{B}\right)^{2}}$
$B I=\sqrt{(1-(-2))^{2}+(0-5)^{2}}$
$B I=\sqrt{(3)^{2}+(-5)^{2}}$
$B I=\sqrt{9+25}$
$B I=\sqrt{34}$
$3)$
$M\left(\frac{x_{A}+x_{B}}{2} ; \frac{y_{A}+y_{B}}{2}\right)$
$M\left(\frac{4-2}{2} ; \frac{3+5}{2}\right)$
$M(1 ; 4)$
$4)$
$N$ l’image du point $M$ par la translation de vecteur $\overrightarrow{A B}$, c’est-à-dire que : $\overrightarrow{M N}=\overrightarrow{A B}$
$\overrightarrow{M N}\left(x_{N}-x_{M} ; y_{N}- _{M}\right)=\overrightarrow{A B}(-6 ; 2)$
$\overrightarrow{M N}\left(x_{N}-x_{M} ; y_{N}-y_{M}\right)=\overrightarrow{A B}(-6 ; 2) $
$\overrightarrow{M N}\left(x_{N}-1 ; y_{N}-4\right)=\overrightarrow{A B}(-6 ; 2)$
Donc : $x_{N}-1=-6$ et $y_{N}-4=2$
Alors : $x_{N}=-5$ et $y_{N}=6$
$1)$
la droite $(AB)$ a une équation réduite de la forme : $\mathrm{y}=\mathrm{ax}+\mathrm{b}$
Calculons $a$ :
$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{4-2}{4-0}=\frac{1}{2}$
Calculons b:
On a: $y=\frac{1}{2} x+b$
Or : $A(0 ; 2) \in(A B)$
Donc : $y_{A}=\frac{1}{2} x_{A}+b$
$2=\frac{1}{2} \times 0+b$
$2=b$
Par conséquent : $(\mathrm{AB}): y=\frac{1}{2} x+2$
$2)$
• Pour $R(0 ;-2)$
$y_{R} =\frac{1}{2} x_{R}+2 $
$-2 =\frac{1}{2} \times 0+2$
$-2=2$ Impossible
Donc le point $R$ n’appartient pas à la droite $( AB )$
• Pour $S(2 ; 3)$
$y_{S}=\frac{1}{2} x_{S}+2 $
$3=\frac{1}{2} \times 2+2 $
$3=3$
Donc le point $S$ appartient à la droite $( AB )$
$3)$
La droite $(D)$ image de la droite $(AB)$ par la translation du vecteur $\overrightarrow{A B}$, c’est-à-dire que : $(D) // (AB)$
Cela signifie qu’elles ont le même coefficient directeur.
On a : $(D)$ : $y=\frac{1}{2} x+b$
Calculons $b$ :
$\boldsymbol{M}(0 ; 3) \in(D)$
Donc : $y_{M}=\frac{1}{2} x_{M}+b$
$3=\frac{1}{2} \times 0+b$
$3=b$
Par conséquent : $(D)$ : $y=\frac{1}{2} x+3$
$4)$
– ( $\Delta$ ) la médiatrice du segment [AB], Cela signifie que $(\Delta) \perp(A B)$ et la droite $(\Delta)$ passe par le milieu du segment $[\mathrm{AB}]$
Calculons $\boldsymbol{a}_{(\Delta)}$ :
$a_{(\Delta)} \times a_{(A B)}=-1$ car $:(\Delta) \perp(\mathrm{AB})$
Donc : $a_{(\Delta)}=\frac{-1}{a_{(A B)}}$
$a_{(\Delta)}=\frac{-1}{\frac{1}{2}}$
$a_{(\Delta)}=-2$
Calculons $b$:
On a: $y=-2 x+b$
Soit $N$ le milieu du segment $[\mathrm{AB}]$ .
Alors: $N\left(\frac{x_{A}+x_{B}}{2} ; \frac{y_{A}+y_{B}}{2}\right)$
$N\left(\frac{0+4}{2} ; \frac{2+4}{2}\right)$
$N(2 ; 3)$
Or : $N(2 ; 3) \in(\Delta)$
Donc : $y_{N}=-2 x_{N}+b$
$3=-2 \times 2+b$
$7=b$
Par conséquent : $(\Delta): y=-2 x+7$
$5)$
On doit résoudre le système suivant : $\left\{\begin{array}{l}y=\frac{1}{2} x+3 \\y=0\end{array}\right.$
Pour $\mathrm{y}=0$ :
$0=\frac{1}{2} x+3 $
$-\frac{1}{2} x=3 $
$-\frac{1}{2} x=\frac{6}{2} $
$-x=6 $
$x=-6$
Le point des coordonnées $( -6 ; 0 )$ est le point d’intersection de la droite $(D)$ et l’axe des abscisses.
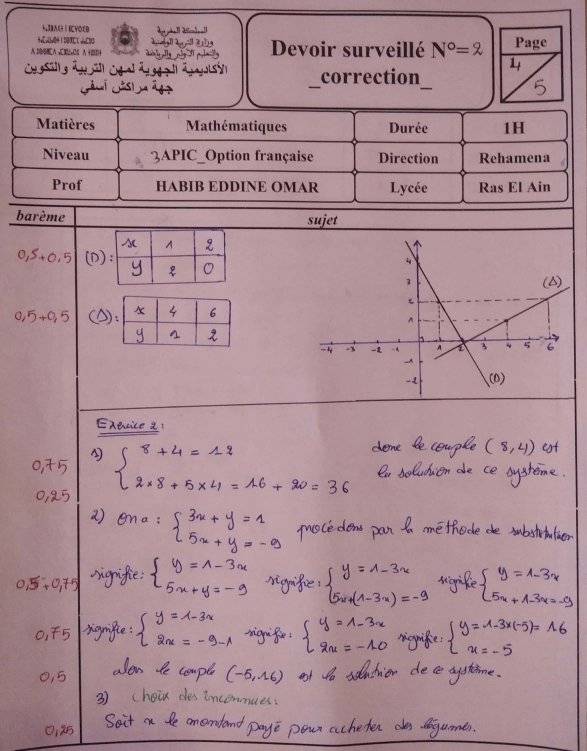
$6)$
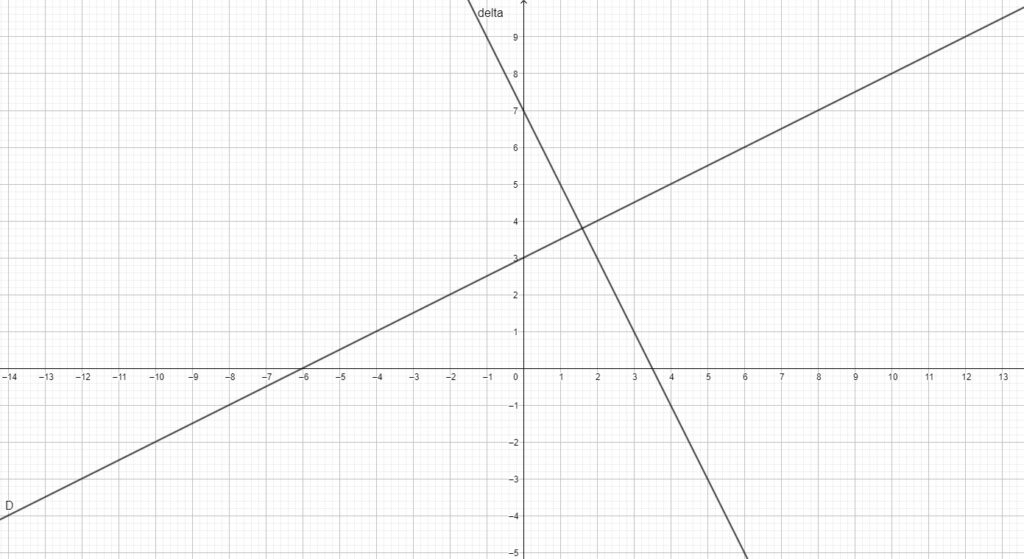
$1)$
$\left\{\begin{array}{l}x-y=20 \\ x+y=130\end{array}\right.$
On a: $x-y=20$
Implique que : $x=20+y$
On remplace x dans la deuxième équation:
$20+y+y=130 $
$2 y=130-20 $
$y=\frac{110}{2} $
$y=55$
Donc la valeur de x est : $x=20+55=75$
$2)$
Soit $x$ le prix payé pour l’achat des légumes et $y$ le prix payé pour l’achat des fruits.
Hamza a payé $130 dh$ pour l’achat de légumes et fruits : $x+y =130$
Le prix des achats de légumes dépasse celui des fruits de $20 dh$ : $x-y=20$
Donc nous avons le système de la question numéro $1$ : $\left\{\begin{array}{l}x-y=20 \\ x+y=130\end{array}\right.$
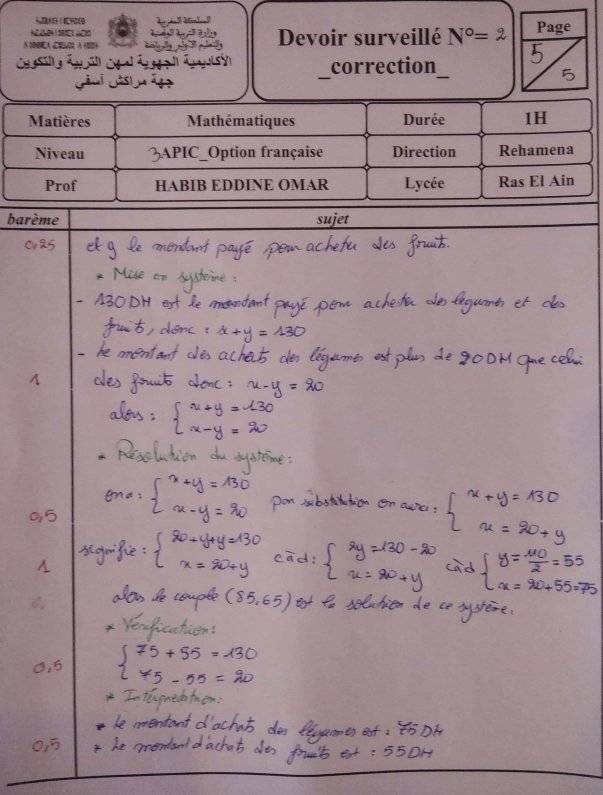
Donc :
Le prix payé pour l’achat des légumes est : $x=75Dh$
Le prix payé pour l’achat des fruits est : $y=55Dh$
Modèle N°2
Exercice 1: $(2 pts)$
Résoudre le système suivant : $\left\{\begin{array}{l}2 x-y=-5 \\ x+2 y=-4\end{array}\right.$
Exercice 2:$(10 pts)$
Le plan est muni d’un repère orthonormé $( O, I, J )$.
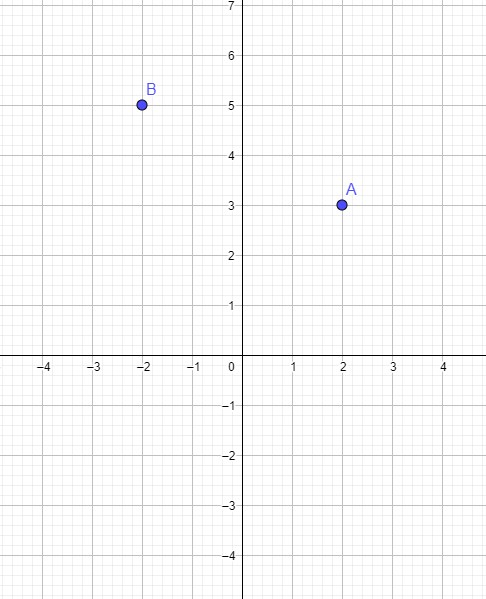
On considère les points $\mathrm{A}(2 ; 3)$ et $\mathrm{b}(-2 ; 5)$.
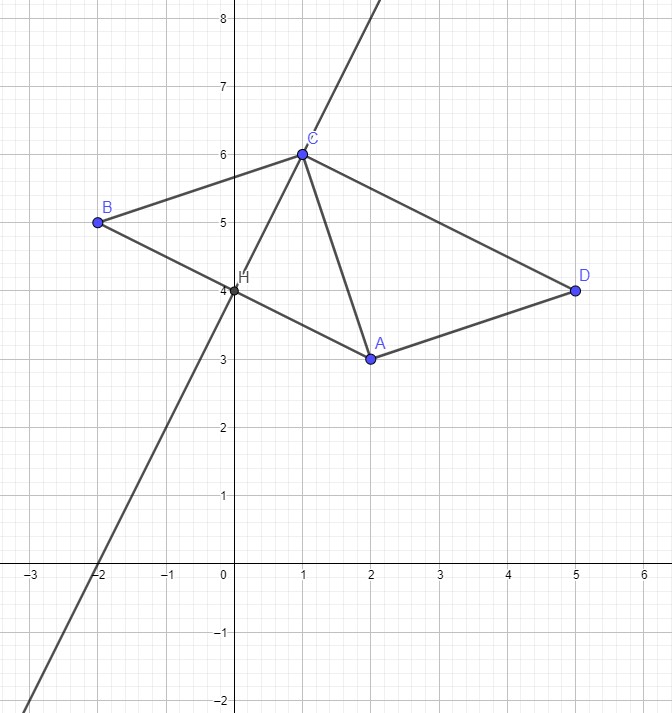
$1)$ Construire les points $A$ et $B$.$ \quad (1 pt)$
$2)$-$a)$Montrer que le coefficient directeur de la droite $(AB)$ est $-\frac{1}{2}$$ \quad (1 pt)$
$b)$ Déduire que l’équation de la droite $(AB)$ est : $y=-\frac{1}{2} x+4$$ \quad (1 pt)$
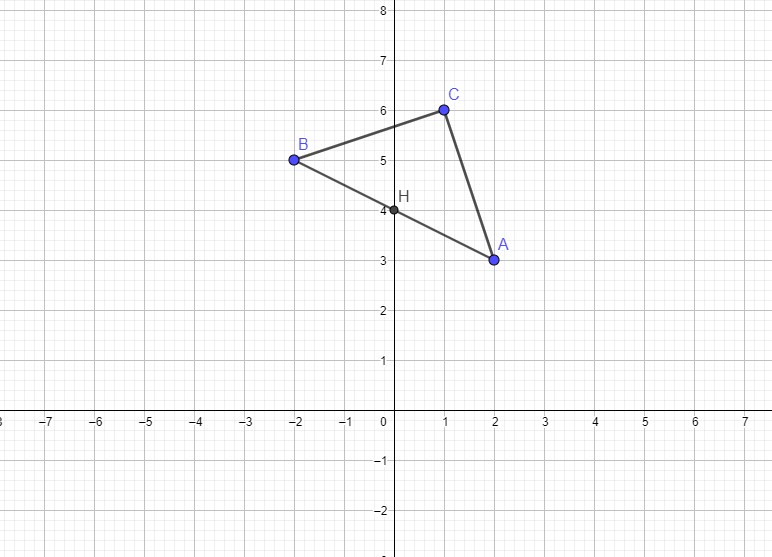
$3)$-$a)$Soit $H$ le milieu du segment $[AB]$. Montrer que $\mathrm{H}(0 ; 4)$$ \quad (1 pt)$
$b)$ Soit ( $\Delta$ ) la médiatrice du segment $[AB]$. Montrer que l’équation du ( $\Delta$ ) est : $y=2 x+4$$ \quad (1 pt)$
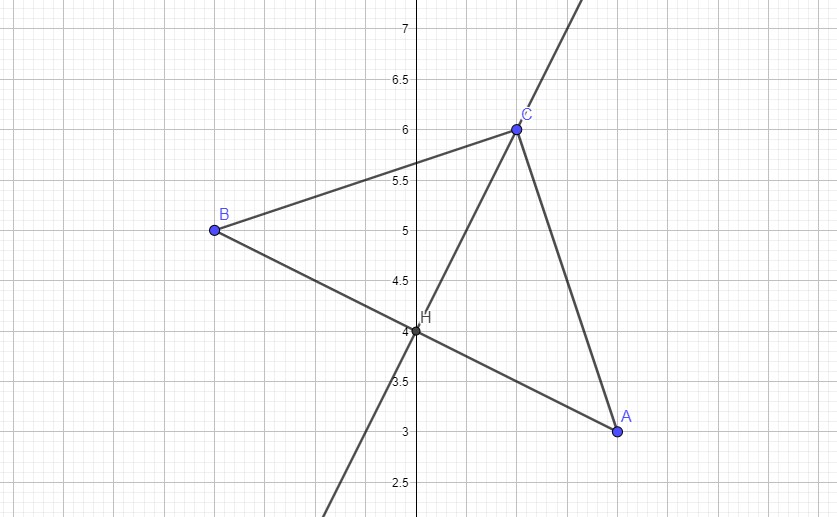
$1)$-$a)$ Montrer que le point $C(1 ; 6)$ appartient à la droite $(\Delta)$.$ \quad (1 pt)$
$b)$ Calculer la distance $BA$.$ \quad (1 pt)$
$c)$Déduire la surface du triangle $ABC$.$ \quad (1 pt)$
$5)$ On considère le point $D(x ; 5-x)$ tel que x un nombre réel.
• Calculer la valeur de $x$, sachant que le quadrilatère $A B C D$ est un parallélogramme puis représenter le point $D$ .$ \quad (1 pt)$
$6)$ Déterminer les coordonnées d point $G$ tel que : $\overrightarrow{C G}=\frac{2}{3} \overrightarrow{C H}$$ \quad (1 pt)$
Exercice 3:$(6 pts)$
Le plan est muni d’un repère orthonormé $(O,I,J)$.
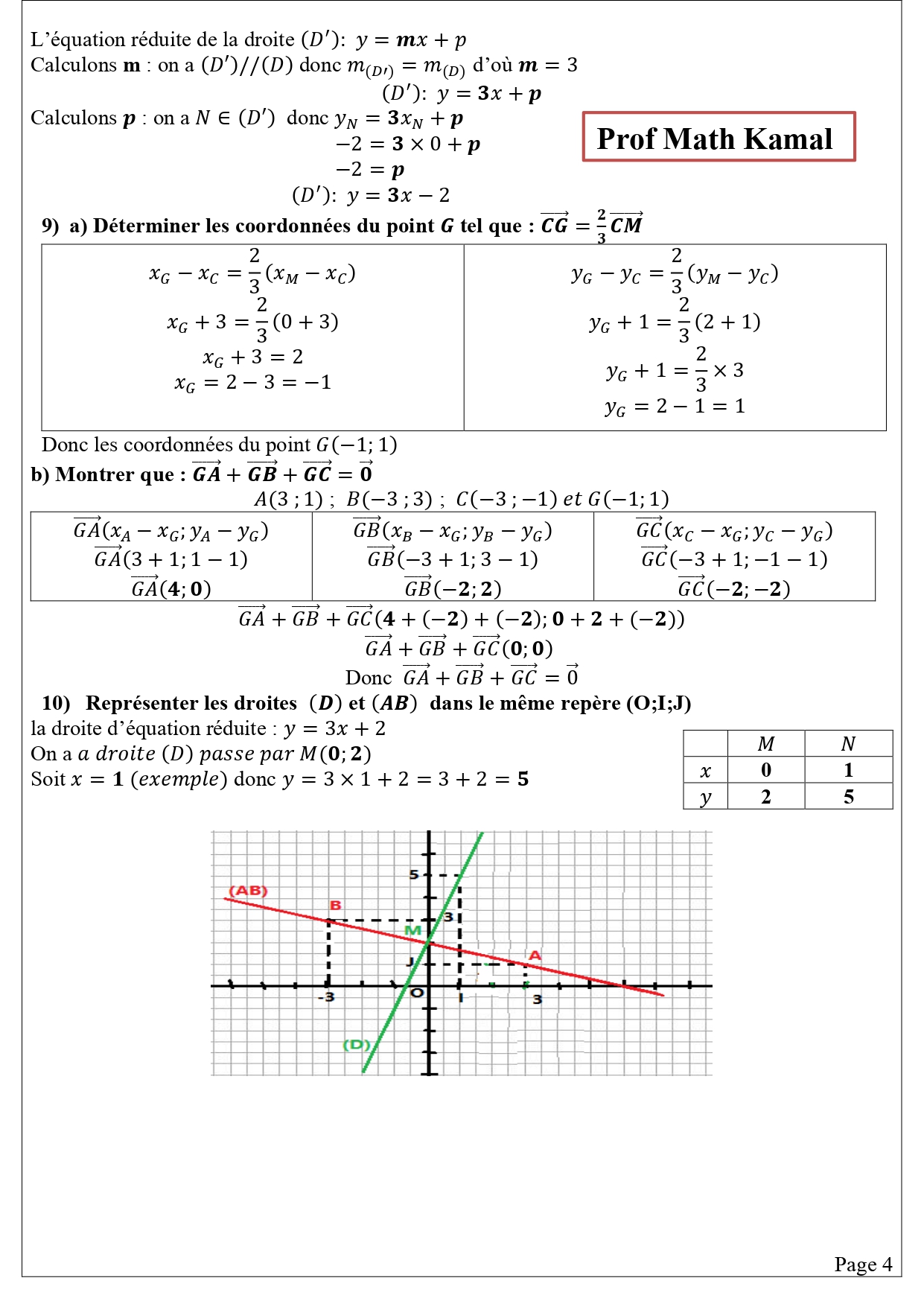
$1)$ Construire la droite $(D)$ d’équation $y=3 x+1$$ \quad (2 pts)$
$2)$ Déterminer l’équation de la droite ( $\mathrm{D}^{\prime}$ ) passant par le point $\mathrm{E}(-1 ; 2)$ et parallèle à la droite $(D)$.$ \quad (2 pts)$
$3)$ Soit $M$ le point d’intersection de la droite $(D)$ avec l’axe des abscisses et $N$ le point d’intersection de la droite $(D)$ avec l’axe des ordonnées.
• Déterminer les coordonnées de $M$ et $N$ . $ \quad (2 pts)$
Exercice 4:$(2 pts)$
On considère le plan muni d’un repère orthonormé ( $\mathrm{O}, \mathrm{I}, \mathrm{J}$ ).
Soient les points $\mathrm{A}(1 ; 1)$, $\mathrm{B}(\frac{1}{2} ; 0)$ et $\mathrm{C}(0 ;-1)$.
$1)$ Montrer que les points $A, B$, et $C$ sont alignés.$ \quad (1 pt)$
$2)$ Déterminer les coordonnées du point $M$ tel que $C$ soit le milieu du segment $[MB]$.$ \quad (1 pt)$
On utilise la méthode d’élimination par combinaison :
$\begin{cases}2 x-y=-5 & \times (1) \\ x+2 y=-4 & \times(-2)\end{cases}$
Le système devient :
$\left\{\begin{array}{l}2 x-y=-5 \\-2 x-4 y=8\end{array}\right.$
On additionne les deux équations membre à membre :
$2 x-y+(-2 x-4 y)=-5+8 $
$2 x-y-2 x-4 y=-5+8 $
$-5 y=3 $
$y=-\frac{3}{5}$
On remplace la valeur de $y$ dans la première équation pour trouver la valeur de $x$ :
$2 x-\left(-\frac{3}{5}\right)=-5 $
$2 x+\frac{3}{5}=-5 $
$2 x=-5-\frac{3}{5} $
$2 x=-\frac{28}{5} $
$x=-\frac{28}{10}=-\frac{14}{5}$
On conclut : le système admet un unique couple solution, qui est : $\left(-\frac{14}{5} ;-\frac{3}{5}\right)$
$1)$
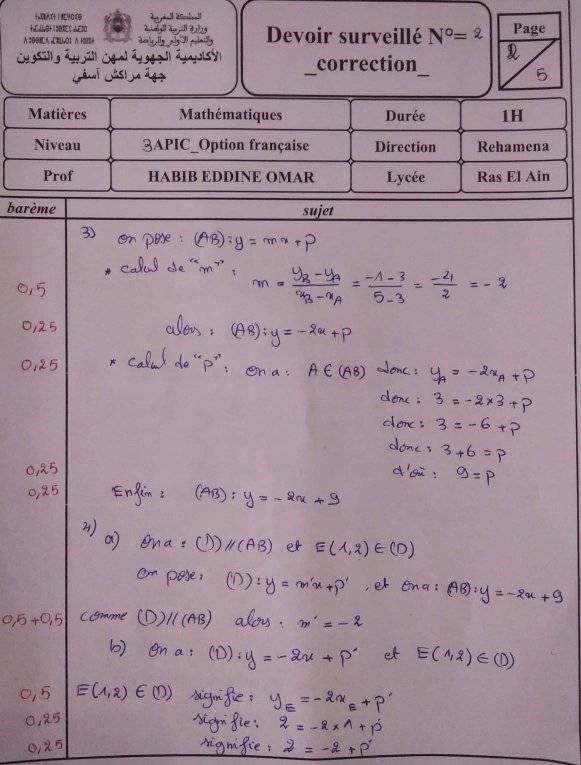
$2)$-$a)$ $a_{(A B)}=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{5-3}{-2-2}=\frac{2}{-4}=-\frac{1}{2}$
$b)$ L’équation de la droite $(AB)$ est : $\boldsymbol{y}=a_{(A B)}{x}+\boldsymbol{b}$
Calculons $b$:
$y_{A}=-\frac{1}{2} x_{A}+b$
$3=-\frac{1}{2} \times 2+b $
$3=-1+b $
$4=b$
Donc l’équation de la droite $(AB)$ est: $y=-\frac{1}{2} x+4$
$3)$-$a)$
$x_{H}=\frac{x_{A}+x_{B}}{2}=\frac{2-2}{2}=0$
$y_{H}=\frac{y_{A}+y_{B}}{2}=\frac{3+5}{2}=4$
Donc: $\mathbf{H}(\mathbf{0} ; 4)$
$b)$
• ( $\Delta$ ) la médiatrice du segment $[\mathrm{AB}]$, Cela signifie que $(\Delta) \perp(\mathrm{AB})$ et la droite $(\Delta)$ passe par $\mathbf{H}(0 ; 4)$ le milieu du segment $[AB]$.
Calculons $\boldsymbol{a}_{(\Delta)}$ :
$a_{(\Delta)} \times a_{(A B)}=-1$ car $:(\Delta) \perp(\mathrm{AB})$
Donc: $a_{(\Delta)}=\frac{-1}{a_{(A B)}}$
Calculons $b$:
On a: $y=2 x+b$
Or : $\boldsymbol{H}(\mathbf{0} ; 4) \in(\Delta)$
Donc: $y_{H}=2 x_{H}+b$
$4=2 \times 0+b$
$4=b$
Par conséquent : $(\Delta): y=2 x+4$
$4)$-$a)$
$y_{C}=2 x_{C}+4 $
$6=2 \times 1+4 $
$6=6$
Donc le point $C$ appartient à la droite ( $\boldsymbol{\Delta}$ )
$b)$
$B A= \sqrt{\left(x_{A}-x_{B}\right)^{2}+\left(y_{A}-y_{B}\right)^{2}}$
$B A =\sqrt{(2-(-2))^{2}+(3-5)^{2}} $
$B A =\sqrt{(4)^{2}+(-2)^{2}} $
$B A =\sqrt{16+4} $
$B A =\sqrt{20}$
$c)$
$S_{A B C}=\frac{\text { la Hauteur } \times \text { la base }}{2} $
$S_{A B C}=\frac{H C \times B A}{2} $
Calculons $HC$:
$H C=\sqrt{\left(x_{C}-x_{H}\right)^{2}+\left(y_{C}-y_{H}\right)^{2}} $
$H C=\sqrt{(1-0)^{2}+(6-4)^{2}} $
$H C=\sqrt{(1)^{2}+(2)^{2}} $
$H C=\sqrt{1+4} $
$H C=\sqrt{5}$
Alors : $S_{A B C}=\frac{\sqrt{5} \times \sqrt{20}}{2}= \frac{\sqrt{100}}{2}$
Donc : $S_{A B C}=5$
$5)$
$ABCD$ est un parallélogramme alors : $\overrightarrow{\boldsymbol{A B}}=\overrightarrow{\boldsymbol{D C}}$
$\overrightarrow{A B}\left(x_{B}-x_{A} ; y_{B}-y_{A}\right)$
$\overrightarrow{A B}(-2-2 ; 5-3) $
$\overrightarrow{A B}(-4 ; 2)$
$\overrightarrow{D C}\left(x_{C}-x_{D} ; y_{C}-y_{D}\right) $
$\overrightarrow{D C}(1-x ; 6-(5-x)) $
$\overrightarrow{D C}(1-x ; 1+x)$
Puisque : $\quad \overrightarrow{A B}=\overrightarrow{D C}$
Alors: $\quad 1-x=-4$
Donc: $\quad x=5$
D’ou : $D(-4 ; 6)$
$6)$
$\overrightarrow{C G}\left(x_{G}-x_{C} ; y_{G}-y_{C}\right) $
$\overrightarrow{C G}\left(x_{G}-1 ; y_{G}-6\right)$
$\overrightarrow{C H}(0-1 ; 4-6)$
$\overrightarrow{C H}(-1 ;-2)$
Puisque : $\quad \overrightarrow{\boldsymbol{C G}}=\frac{2}{3} \overrightarrow{\boldsymbol{C H}}$
Alors : $\quad x_{G}-1=\frac{2}{3} \times(-1) \quad$ et $\quad y_{G}-6=\frac{2}{3} \times(-2)$
Donc : $\quad x_{G}-1=\frac{-2}{3} \quad$ et $\quad y_{G}-6=\frac{-4}{3}$
Donc : $\quad x_{G}=\frac{1}{3}$ et $\quad y_{G}=\frac{14}{3}$
$G\left(\frac{1}{3} ; \frac{14}{3}\right)$
$1)$
$\begin{array} {|r|r|}\hline x & 0 & 1 \\ \hline y & 1 & 4 \\ \hline \end{array}$
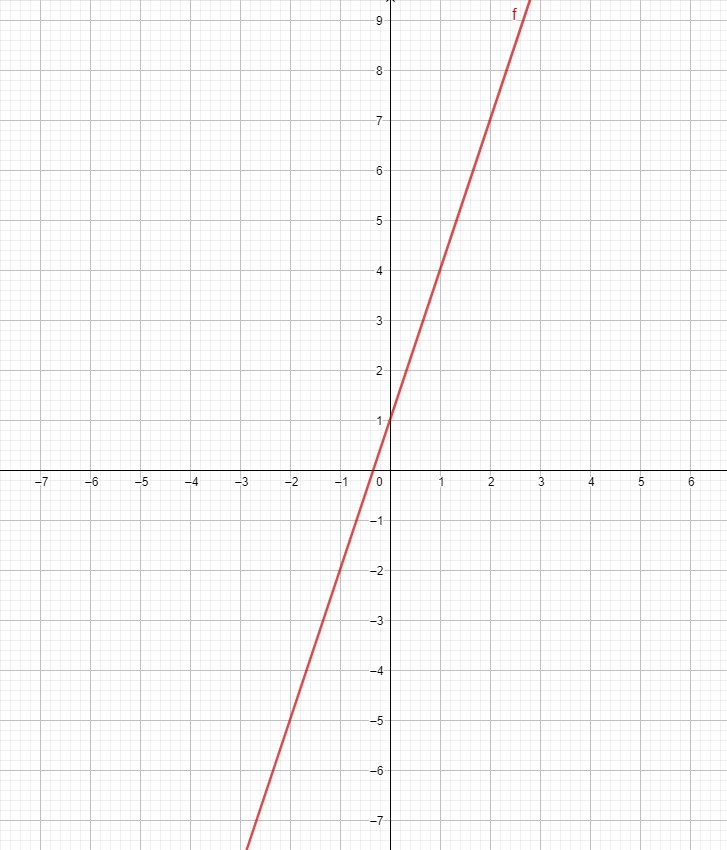
$2)$
( $D^{\prime}$ ) // (D) cela signifie qu’elles ont le même coefficient directeur
On a: (D’) : $y=3 x+b$
Calculons $b$:
$E(-1 ; 2) \in\left(D^{\prime}\right)$
Donc: $y_{E}=3 x_{E}+b$
$2=3 \times(-1)+b$
$2=-3+b$
$5=b$
Par conséquent : (D’) : $y=3 x+5$
$3)$
Soit $M$ le point d’intersection de la droite $(D)$ avec l’axe des abscisses : c’est-à-dire on doit résoudre le système suivant :
$\left\{\begin{array}{l}y=3 x+1 \\y=0\end{array}\right.$
$\left\{\begin{array}{l}0=3 x+1 \\y=0\end{array}\right.$
$\left\{\begin{array}{l}x=\frac{-1}{3} \\y=0\end{array}\right.$
$ M\left(-\frac{1}{3} ; 0\right)$
• $N$ le point d’intersection de la droite $(D)$ avec l’axe des ordonnées, c’est-à-dire on doit résoudre le système suivant :
$\left\{\begin{array}{l}y=3 x+1 \\x=0\end{array}\right.$
$\left\{\begin{array}{l}y=3 \times 0+1 \\x=0\end{array}\right.$
$\left\{\begin{array}{l}y=1 \\x=0\end{array}\right.$
$N(0 ; 1)$
$1)$
$\overrightarrow{A B}\left(x_{B}-x_{A} ; y_{B}-y_{A}\right) $
$\overrightarrow{A B}\left(\frac{1}{2}-1 ; 0-1\right) $
$\overrightarrow{A B}\left(-\frac{1}{2} ;-1\right) $
$\overrightarrow{A C}\left(x_{C}-x_{A} ; y_{C}-y_{A}\right) $
$\overrightarrow{A C}(0-1 ;-1-1) $
$\overrightarrow{A C}(-1 ;-2)$
Puisque : $\overrightarrow{A B}=\frac{1}{2} \overrightarrow{A C}$
Alors les points $A, B$, et $C$ sont alignés.
$2)$ $C$ est le milieu du segment $ [MB]$ :
$x_{C}=\frac{x_{M}+x_{B}}{2}$
$y_{C}=\frac{y_{M}+y_{B}}{2}$
$0=\frac{x_{M}+\frac{1}{2}}{2}$
$-1=\frac{y_{M}+0}{2}$
$0=x_{M}+\frac{1}{2}$
$-2=y_{M}+0$
$x_{M}=-\frac{1}{2}$
$y_{M}=-2$
$M\left(-\frac{1}{2} ;-2\right)$
Dans un repère orthonormé (O, I, J). On considère les points A(1,−1); B(2, 1) et C(0, 2).
1. Représenter les points précédents dans le repère.
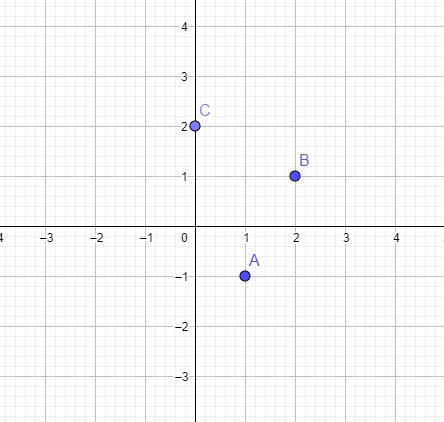
2. (a) Calculer les distances AB, AC, et BC.
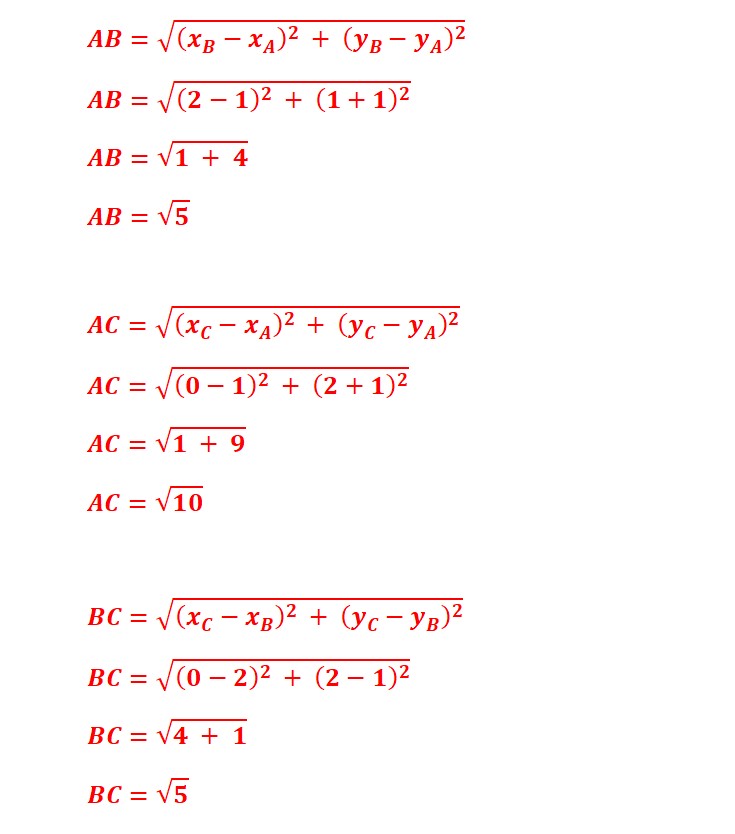
(b) Déduire la nature du triangle ABC.
AB=BC et AB² + BC² = AC² , donc ABC est un triangle rectangle et isocèle.
3. (a) Calculer le coefficient directeur des droites (AB) et (BC).
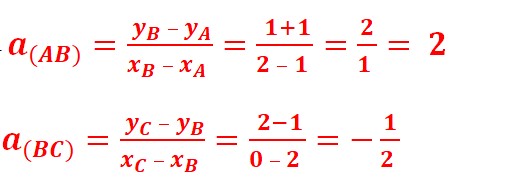
(b) Déduire que (AB) ⊥ (AC)
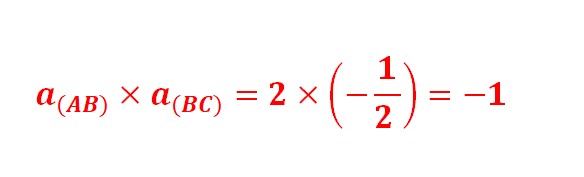
4. Déterminer les coordonnées du point H le centre du cercle circonscrit au triangle ABC.
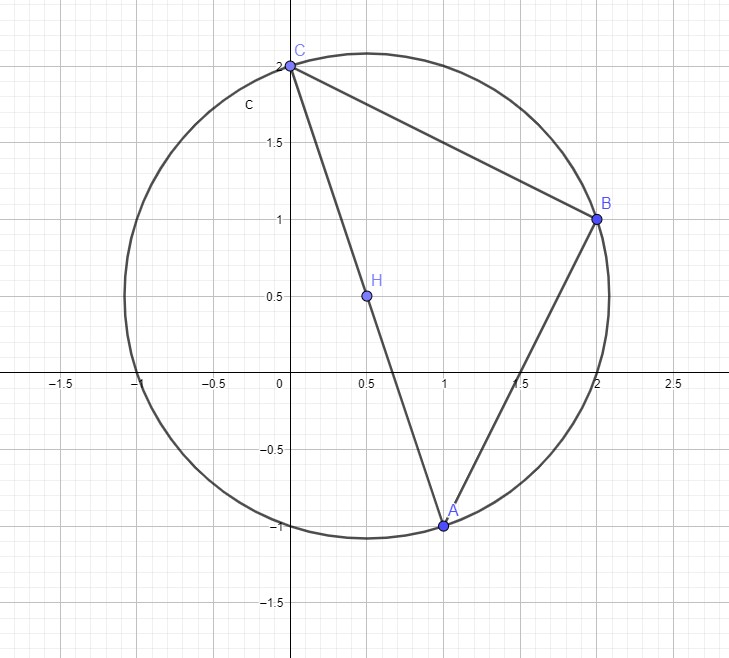
D’après la figure le point H est le milieu du segment [AC].
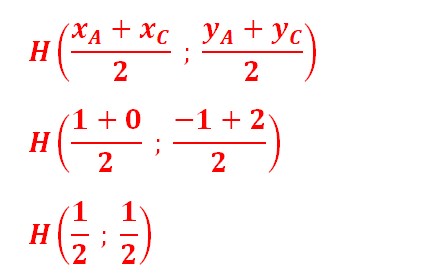
Le plan est muni d’un repère orthonormé (O, I, J). On considère les points A(2; 3) et B(−2; 5)
1. Construire les points A et B.
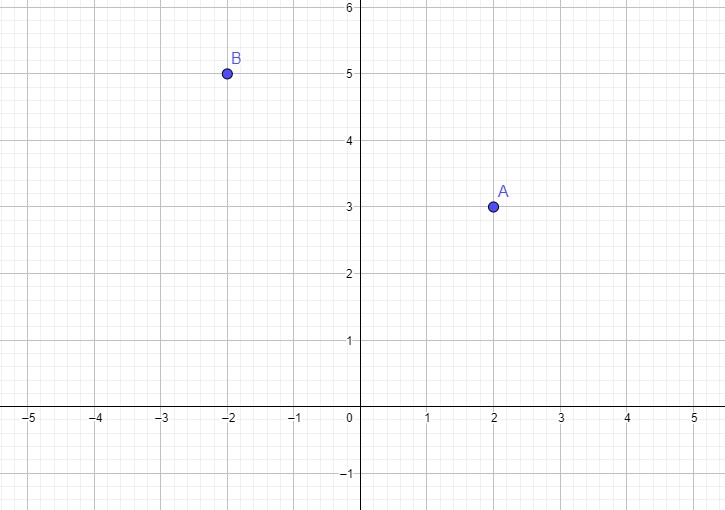
2. (a) Montrer que le coefficient directeur de la droite (AB) est −1/2
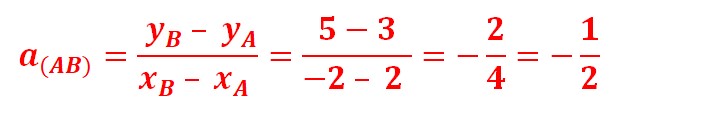
(b) Déduire que l’équation de la droite (AB) est : y =(−1/2)x + 4

3. (a) Soit H le milieu du segment [AB]. Montrer que H(0; 4).
(b) Soit (Δ) la médiatrice du segment [AB].
Montrer que l’équation du (Δ) est : y = 2x+4

4. (a) Montrer que le point C(1; 6) appartient à la droite (Δ).

(b) Calculer la distance BA.
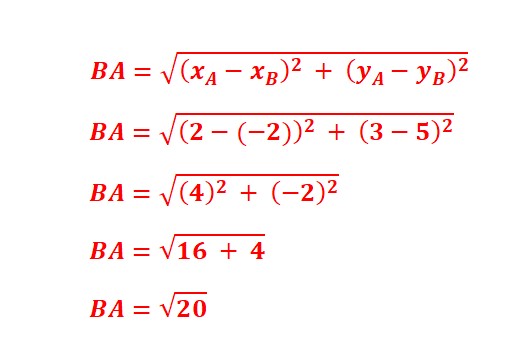
(c) Déduire la surface du triangle ABC.
La surface du triangle ABC:

5. On considère le point D(x; 9−x) tel que x un nombre réel.
Calculer la valeur de x, sachant que le quadrilatère ABCD est un parallélogramme puis représenter le point D.

6- (a) Déterminer les coordonnées d point G tel que :
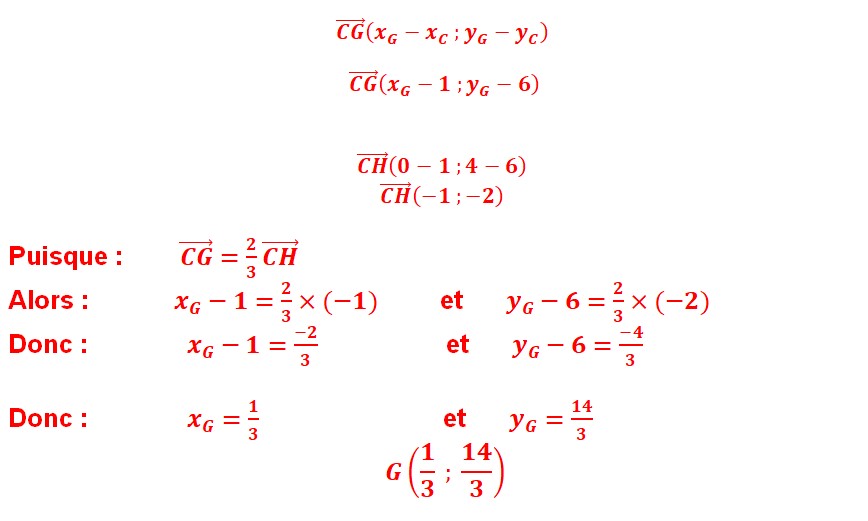
(a) Résoudre le système suivant :

(b) Résoudre le problème suivant :
Quel âge avez-vous?, demande un élève à son Professeur. Et ce dernier répond par une énigme : » Il y a 5 ans, je dépassais les deux-tiers de ton âge le quadruple de celui-ci. Dans 1 an, il faudra multiplier ton âge par 16/5 pour
trouver le mien! ». Quels âges ont-ils?
Soit y l’âge de l’élève et x celui du professeur.
• Il y a 5 ans , je dépassais les deux-tiers de ton âge le quadruple de celui-ci.
On a alors x – 5 = 4(y – 5) + (2/3)(y – 5), c’est-à-dire 3(x – 5) = 12(y – 5) + 2(y – 5) ce qui équivaut à 3x – 14y= -55.
• Dans 1 ans, ils auront x + 1 et y + 1 ans et on a donc (x + 1) = (16/5)(y + 1) , c’est-à-dire 5(x + 1) = 16(y + 1) , ce qui équivaut à 5x – 16y = 11
On a donc le système suivant , qu’on a résolu à la question (a).
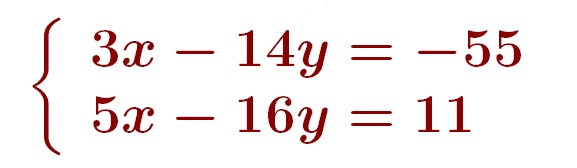
Le professeur a donc 47 ans et l’élève a 14 ans.
Devoirs Corrigés Maths N°2 S2 3AC