Devoirs Corrigés Maths N°3 S1 3AC

Devoir N°3 Semestre 1

Modèle N°1

Exercice 1：$(4×0,5=2$ pts)

$1)$  Compléter par: Vrai ou Faux

* Dans un triangle rectangle, l’hypoténuse est le plus grand côté$……..$

* Le sinus d’un angle aigu est égal au quotient du côté adjacent sur l’hypoténuse$……..$

* Si $\hat{x}$ un angle aigu, alors : $\cos {\hat{x}} +\sin {\hat{x}} =1$$……..$

* Si un angle inscrit et un angle au centre interceptent le même arc, alors ils ont la même mesure$……..$

Exercice 2：$(1,5+1,5+1,5+2+1,5=8$ pts)

$1)$ Soit $E F G$ un triangle, avec : $E F=4 ; E G=2 \sqrt{5}$ et $F G=6$.

• Montrer que $E F G$ est un triangle rectangle et préciser en quel sommet.

$2)$ Calculer $: \boldsymbol{\operatorname { c o s }} \widehat{\boldsymbol{F}};  \boldsymbol{\operatorname { s i n }} \widehat{\boldsymbol{F}} ; \boldsymbol{\operatorname { t a n }} \widehat{\boldsymbol{F}}$

$3)$ Calculer $: \boldsymbol{\operatorname { c o s }} \widehat{\boldsymbol{G}} ; \sin \widehat{\boldsymbol{G}} ; \tan \widehat{\boldsymbol{G}}$

$4)$ Soit $I$ le milieu de $[E F]$ et $H$ sa projeté orthogonal sur la droite (FG).

$4-1) $ Calculer $I G$.

$4-2)$ Calculer $I H$.

Exercice 3：$(1 + 1+ 1,5+1,5+2=7$ pts)

Soit un triangle $EDF$ rectangle en $D$.

$1)$  Soit $x$ un angle aigu tel que : $\cos x=\frac{2}{5}$.

$1-1)$ Calculer: $\sin x$

$1-2)$ Calculer: $\tan x$

$2)$ Calculer :

 $A=2 \cos ^{2} 17^{\circ}+1+2 \sin ^{2} 17^{\circ}$

$B=3 \sin ^{2} 10^{\circ}+\sqrt{5} \cos 20^{\circ}+3 \sin ^{2} 80^{\circ}-\sqrt{5} \sin 70^{\circ}-\tan 50^{\circ} \times \tan 40^{\circ}$

$3)$ Montrer que : $\frac{(\cos x+\sin x)^{2}-1}{1-\cos ^{2} x}=\frac{2}{\tan x}$

Exercice 4：$(1 + 1+ 1 = 3$ pts)

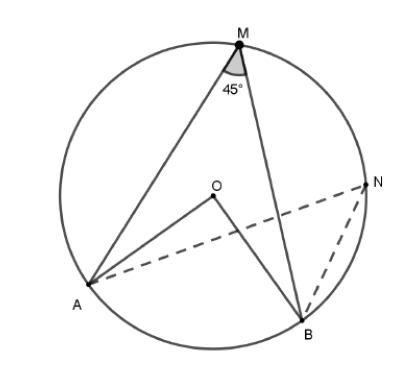
Soit la figure ci-contre tel que $O$ est le centre du cercle.

$A, B, N$ et $M$ sont des points du cercle tel que : $\widehat{A M B}=45^{\circ}$.

$1)$ Déterminer la mesure de l’angle $\widehat{A N B}$. Justifier votre réponse.

$2)$ Déterminer la mesure de l’angle $\widehat{A O B}$. Justifier votre réponse.

$3)$ Déduire que le triangle $A O B$ est rectangle isocèle.

🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.


Je m’abonne maintenant

Modèle N°2

Exercice 1：$(4×1,5=6$ pts)

Soit $E F G$ un triangle tel que: $E F=5 ; E G=1 2$ et $F G=13$ .

• Calculer $\cos \hat{F}$ , $\tan \hat{F}, \sin \hat{F} \quad et \quad \sin \hat{G}$  .

Exercice 2：$(2 + 2+ 2+1,5+1,5=9$ pts )

$1)$ Soit $x$ un angle aigu tel que :$ \frac{4 \cos x-9 \sin x}{2 \cos x-3 \sin x}=4 $

• Calculer  $\tan x$

$2)$ Soit $x$ un angle aigu tel que : $\cos x-\sin x=\sqrt{2} \cdot \sin x$

$a)$ Montrer que: $\cos x+\sin x=\sqrt{2} \cos x$

$b)$ Calculer $\cos x$ et $\sin x$

$3)$ Calculer

$ A=3 \cos 37^{\circ}+\sin ^{2} 19^{\circ}+\sin ^{2} 71^{\circ}+3 \cos ^{2} 53^{\circ} $

$ B=\frac{1}{\tan ^{2} 57^{\circ}+1}-\frac{\tan ^{\circ} 33^{\circ}}{\tan ^{2} 33^{\circ}+1}$

Exercice 3：$(1,5+2+1,5=5$ pts )

Soit la figure ci-contre tel que $\theta$ est le centre du cercle.

$A, B, C$ et $M$ sont des points du cercle tel que: $A B C$ est un triangle équilatéral.

$1)$ Déterminer la mesure de l’angle $A \widehat{M }B$. Justifier votre réponse.

$2)- a)$ Déterminer la mesure de l’angle $A \widehat{M }C$, puis déduire la mesure de l’angle $B \widehat{M }C$.

$b)$ Déterminer la mesure de l’angle $\hat{A O B}$

🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.


Je m’abonne maintenant

 

Niveau : 3APIC

Modèle N°3

Durée : 1 Heure 

Exercice 1 (4 points)

Soit \( ABC \) un triangle tel que : \( AC = \sqrt{52}cm \) ; \( BH = 9cm \) et \( HC = 4cm \).

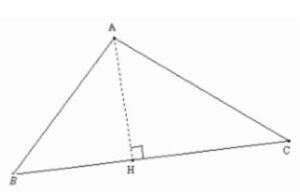
  1. Calculer \( AH \). (1 point)
  2. Calculer \( AB \). (1 point)
  3. Montrer que \( ABC \) est un triangle rectangle. (2 points)

Exercice 2 (7 points)

Soit \( ABCD \) un trapèze rectangle tel que : \( AB = 4cm \) ; \( AD = 3cm \) ; \( DC = 7cm \) ; \( BC = 2\sqrt{6}cm \).

 

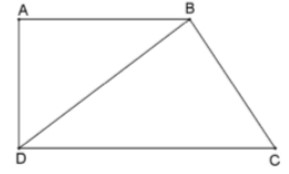
  1. Calculer \( BD \). (1 point)
  2. Montrer que \( BCD \) est un triangle rectangle. (2 points)
  3. Calculer : \( \cos \hat{B} \) ; \( \sin \hat{B} \) ; \( \tan \hat{B} \). (2 points)
  4. Soit \( H \) le projeté orthogonal du point \( A \) sur la droite (\( BD \)).
    Calculer : \( AH \) et \( DH \). (2 points)

Exercice 3 (7 points)

  1. Soit \( \hat{x} \) un angle aigu tel que : \( \sin x = \frac{\sqrt{3}}{2} \).
    Calculer : \( \cos x \) et \( \tan x \). (2 points)
  2. Calculer :

    \( A = 2\sin^2 13^\circ + \sin^2 35^\circ + \cos^2 35^\circ + 2\cos^2 13^\circ \)

    \( B = \sin^2 33^\circ + 3 \times \tan 50^\circ \times \tan 40^\circ + \sin^2 57^\circ \)

    \( C = 3 \sin 31^\circ + 7\sin^2 53^\circ – 3 \cos 59^\circ + 7\sin^2 37^\circ \)

    (3 points)

  3. Simplifier :

    \( A = \tan 20^\circ \times \sin 70^\circ – \cos 70^\circ \)

    \( B = \tan^2 x – \tan^2 x \times \sin^2 x + \cos^2 x \)                                     (2 points)

Exercice 4 (2 points)

On considère la figure ci-jointe où (C) est un cercle de centre O et les points \( A, B, D, E, F, J \) et \( M \) appartiennent au cercle (C).
Et \( \overline{ADB} = 76^\circ \) et \( EFJ = 55^\circ \).

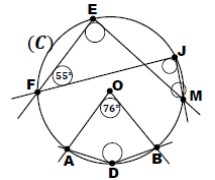
  1. Calculer \( EMJ \). (1 point)
  2. Montrer que : \( \overline{ADB} = 142^\circ \). (1 point)

Barème total : 20 points

🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.


Je m’abonne maintenant

Devoirs Corrigés Maths N°3 S1 3AC