ℵ Devoir N°3 Modèle 1
ℵ Devoir N°3 Modèle 2
ℵ Devoir N°3 Modèle 3
ℵ Devoir N°3 Modèle 4
ℵ Devoir N°3 Modèle 5
1)-Cocher (×) la bonne ou les bonnes réponses :
a) pour un conducteur ohmique, On exprime la loi d’ohm par la relation :
𝑈 = 𝑅 × 𝐼
b) la puissance électrique reçue par un appareil de chauffage est donné par la relation :
𝑃 = 𝑈 × 𝐼 et 𝑃 = 𝑅 × 𝐼²
2)- compléter le tableau suivant :
3)-Répondre par « vrai » ou « faux »
-un appareil électrique fonctionne normalement sous ses caractéristiques nominales Vrai
-une lampe de tension nominale 12V traversée par un courant 2A consomme une puissance nominale égale à 22W Faux
1) Une lampe est traversée par un courant de 2 A, la tension entre ses bornes est 24 V.
a) Calculer sa résistance R :
On a : R = U/I
A.N : R = 24 / 2
R = 12 Ω
b) Calculer sa puissance électrique P :
P = U × I
P = 24 × 2
P = 48 W
2) Un fer à repasser porte les indication suivante (220V ;1200W)
a) Donner la signification physique de chaque indication :
220V : La tension électrique nominale
1200W : La puissance électrique nominale
b) Calculer l’intensité du courant électrique nominale I qui traverse cette Fer à repasser :
On a : P = U × I
Alors : I = P / U
A.N : I = 1200 / 220
I = 5,45 A
c) Calculer la valeur de la résistance électrique R de cette Fer à repasser :
On a : R = U/I
A.N : R = 220 / 5,45
R = 40,37 Ω
3) Dans une installation domestique une famille fait fonctionner chaque jour :
-Un téléviseur (220V ; 88W)
– Machine à laver de puissance (220V ; 2,1KW)
-Un lustre composé de 6 lampes identiques chaque lampe caractérisée par (220V ; 100W)
a) Calculer la puissance totale de tous les appareils
P(totale) = P(téléviseur) + P(Machine à laver) + 6×P(lampes)
P(totale) = 88 + 2100 + 6×100
P(totale) = 2788 W
b) sachant que Le disjoncteur est réglé sur Imax= 35 A et U=220V. Est-il possible d’utiliser
simultanément tous les appareils ? justifier
La puissance totale ne doit pas dépasser la puissance maximale Pmax spécifiée pour la maison par l’Agence de distribution d’électricité
Pmax = U×Imax
Pmax = 220×35
Pmax = 7700 W
Puisque : P(totale)<Pmax
il est possible d’utiliser simultanément tous les appareils
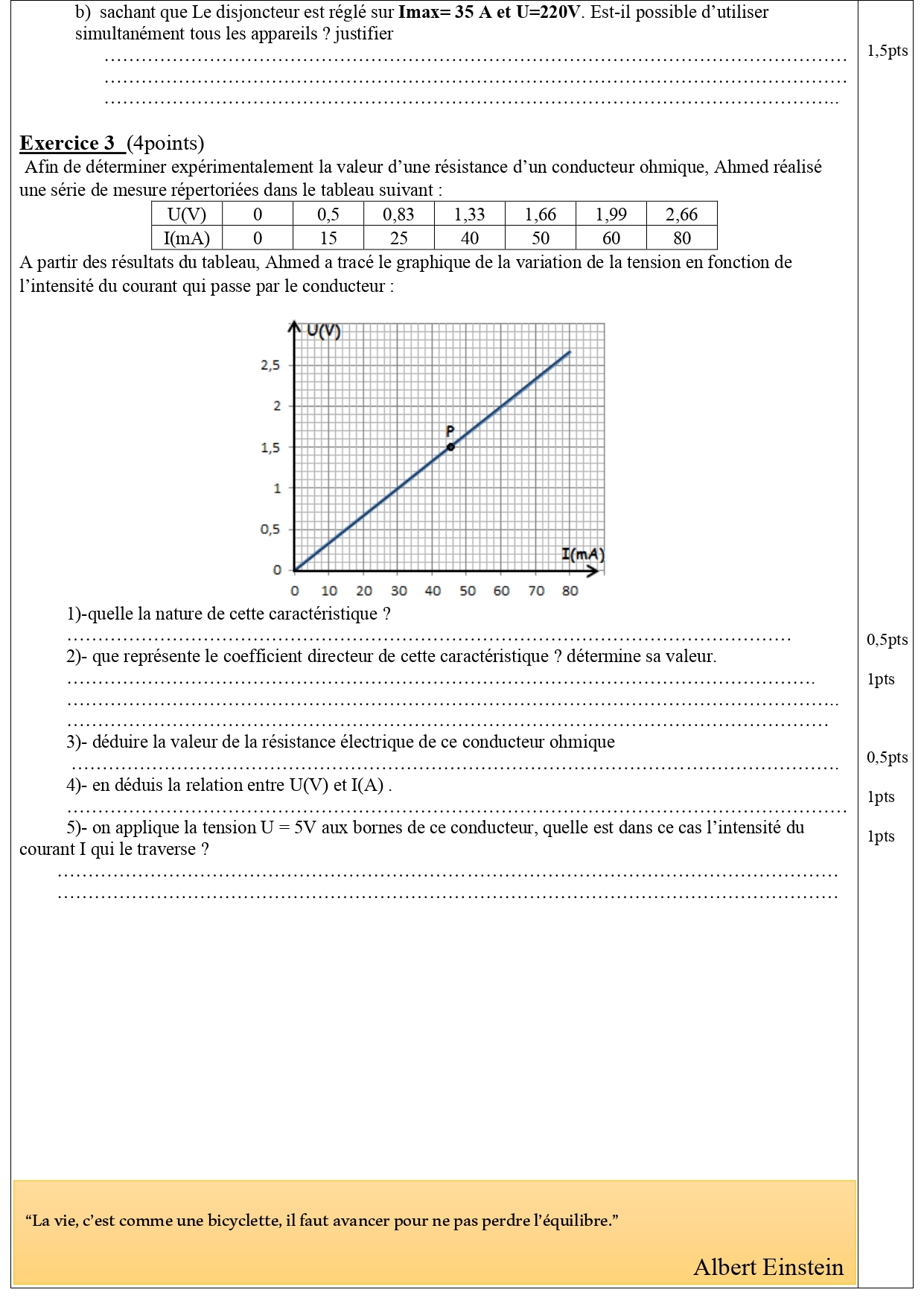
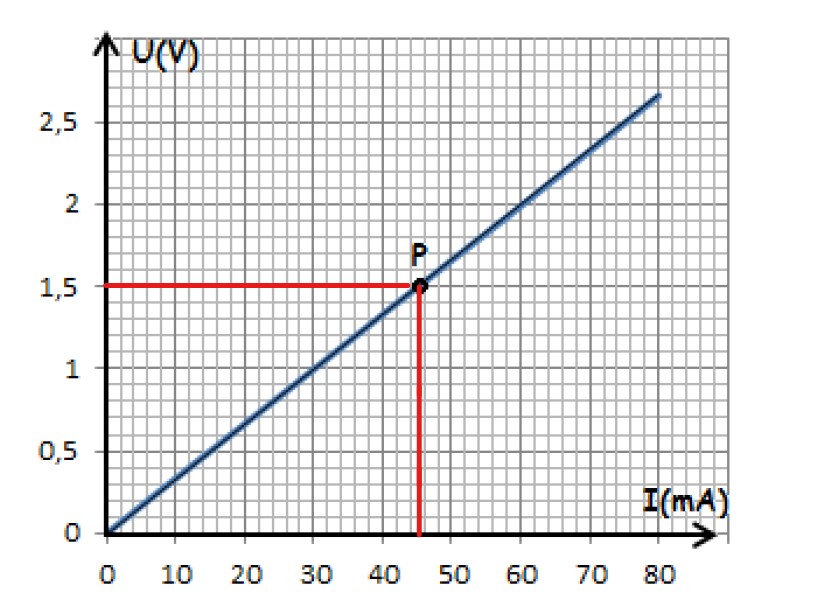
Afin de déterminer expérimentalement la valeur d’une résistance d’un conducteur ohmique, Ahmed réalisé
une série de mesure répertoriées dans le tableau suivant :
A partir des résultats du tableau, Ahmed a tracé le graphique de la variation de la tension en fonction de
l’intensité du courant qui passe par le conducteur :
1)-Quelle la nature de cette caractéristique ?
La caractéristique étant une droite passant par l’origine de repère
2)- Que représente le coefficient directeur de cette caractéristique ? détermine sa valeur.
la tension et l’intensité sont proportionnelles.
a = U / I
sa valeur :
d’après la courbe :
U = 1,5 V et I = 45 mA
a = U / I
a = 1,5 / 0,045
a = 33,33 V/A
3)- Déduire la valeur de la résistance électrique de ce conducteur ohmique
R = a = 33,33 Ω
4)- En déduis la relation entre U(V) et I(A) .
U = R×I
5)- On applique la tension U = 5V aux bornes de ce conducteur, quelle est dans ce cas l’intensité du
courant I qui le traverse ?
d’aprés la loi d’ohm : U = R×I
Alors : I = U / R
A.N : I = 5 / 33,33
I = 0,15 A = 150 mA
1. Compléter les phrases par les mots qui convient : ( 2 .5Pt):
Watt – intensité – U – ampère – produit – puissance – tension – volt – I
➢ La puissance nominale d’une lampe est égale au produit de sa tension nominale par
l’intensité du courant électrique qui la traverse en fonctionnement normal.
➢ La puissance P reçue par une lampe s’exprime par la relation suivante dans laquelle on
précisera les unités employées : P = U×I avec P exprimée en Watt , U exprimée en volt
et I exprimée en ampère
2. Répondre par vrai ou faux : (2 pt)
• Pour calculer la résistance d’un appareil de chauffage on utilise : P=R²×I faux
• L’unité de la puissance électrique dans le système international d’unités est : Le Watt-heure vrai
• La loi d’ohm relative à un conducteur ohmique s’exprime par la relation : U = R×I vrai
• La puissance électrique est mesurée par un compteur électrique faux
3. Cocher la bonne réponse: (1.5 pt)
➢ Une lampe qui consomme une puissance électrique inférieure à sa puissance nominale :
Brille normalement – grille – brille faiblement.
➢ Une lampe de tension nominale 12V traversée par un courant de 200mA consomme une
puissance égale à :
2,4W – 24W – 240W – 2400W.
➢ Une lampe porte l’indication (6V-1,8W) ; en fonctionnement normal, l’intensité du courant
vaut-elle : 0,3A – 0,18A – 0,6A
4. Complétez le tableau par ce qui convient? (2pt)
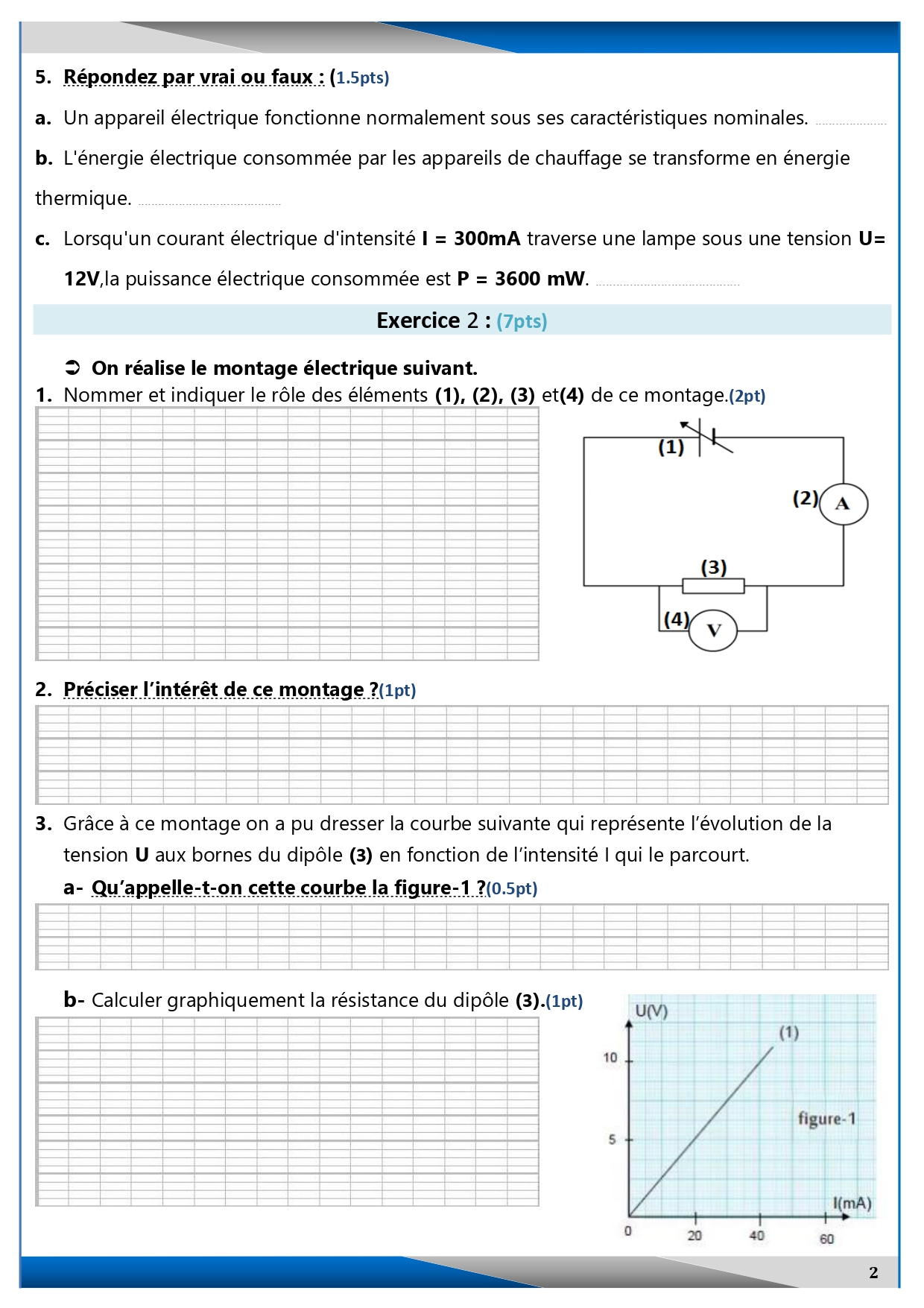
I. Partie I : La figure ci-dessous représente la caractéristique d’un conducteur ohmique :
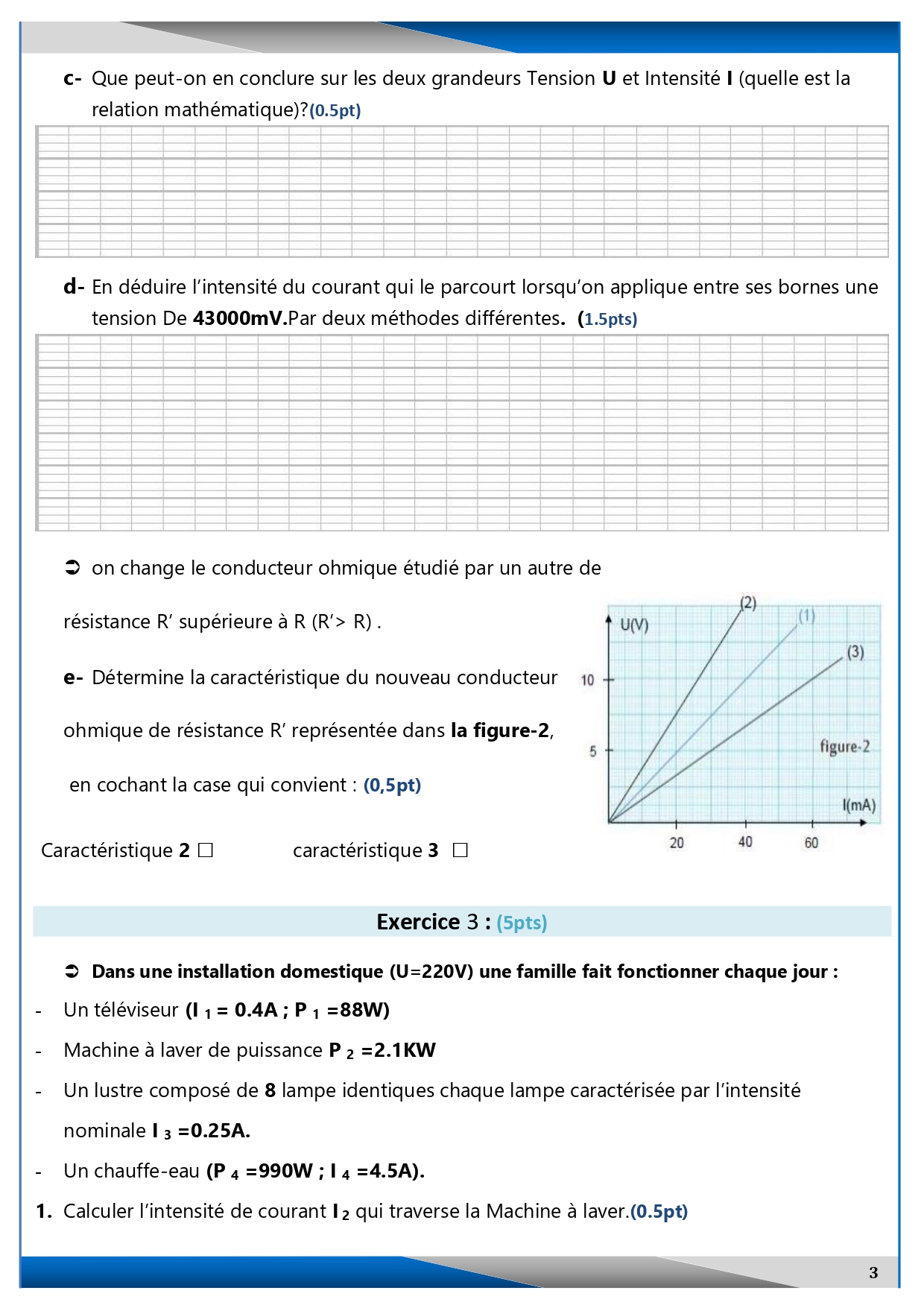
1) Déterminer l’intensité I du courant électrique traversant le conducteur ohmique lorsque nous appliquons entre ses bornes une tension U = 2V. (1.pt)
I = 0,2 A
2) Déterminer la valeur de la résistance de ce conducteur ohmique à partir du graphique. (1pt)
On a : R = U/I
R = 2/0,2
R = 10 Ω
3) Sachant que la résistance est alimentée par la tension U = 4V, calculer, en Watt, La puissance électrique consommée par la résistance précédente. (2pt)
On a : P = U²/R
A.N : P = 4²/10
P = 16/10
P = 1,6 W
II. Partie II :
➢ Le montage électrique ci-contre se compose d’un générateur, d’une lampe, d’un conducteur ohmique, d’un ampèremètre et d’un interrupteur.
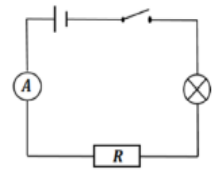On observe que l’éclairage de la lampe est faible.
1. Réponds par vrai ou faux : (1pt)
a – la puissance électrique consommée par la lampe est inférieure à sa puissance nominale Vrai
b – la puissance électrique consommée par la lampe est supérieure à sa puissance nominale. Faux
2. L’ampèremètre indique la valeur I = 0,05 A .
a )– Donne l’énoncé de la loi d’ohm d’un conducteur ohmique. (1pt)
La tension U aux bornes d’un conducteur ohmique est égale au produit de sa résistance R par l’intensité I du courant qui le traverse.
U = R×I
B) – Détermine la valeur de la tension électrique U aux bornes du conducteur ohmique.
on donne : R = 100 Ω. (1pt)
U = R×I
U = 100×0,05
U = 5V
c) – Détermine P la puissance électrique consommée par le conducteur ohmique. (1pt)
P = U×I
P = 5×0,05
P = 0.25 W2
