Droites remarquable dans le triangle exercices corrigés 2AC
Exercice 1:
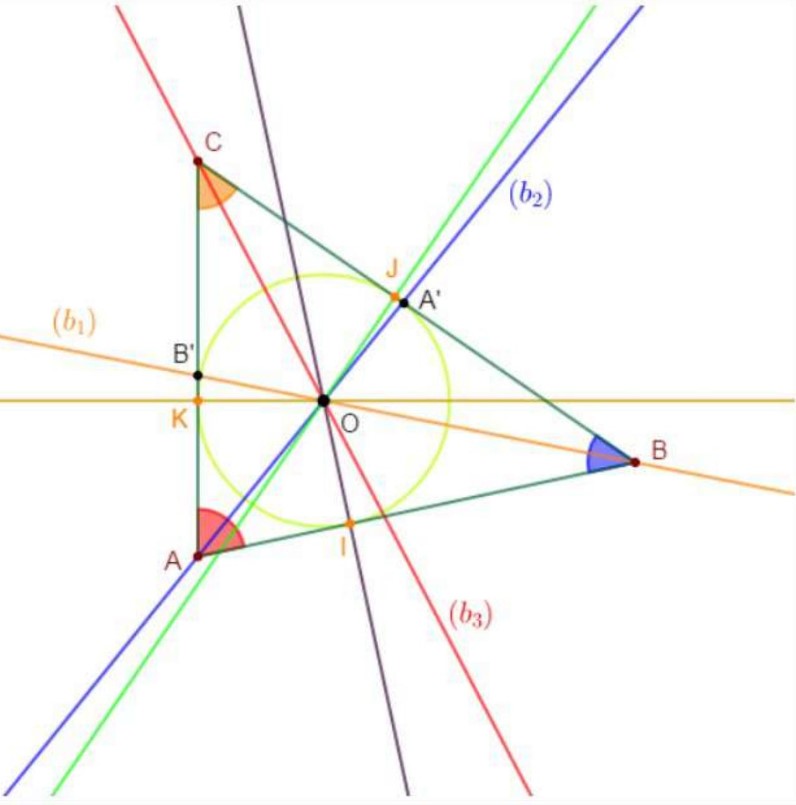
$1)$ Construire un triangle $A B C$ quelconque.
$2)$ $a)$ Construire ( $b_{2}$ ) bissectrice de l’angle $\widehat{A}$; elle coupe $(B C)$ en $A^{\prime}$.
$b)$ Construire la droite $\left(b_{1}\right)$ bissectrice de l’angle $\widehat{B}$; elle coupe $(A C)$ en $B^{\prime}$.
$3)$ $a)$ ( $b_{1}$ ) et ( $b_{2}$ ) se coupent en $O$, marque $O$.
$4)$$a)$ Construire la droite perpendiculaire à $(A B)$ et passant par $O$ coupe la droite ( $A B$ ) en $I$.
$b)$ Construire la droite perpendiculaire à $(B C)$ et passant par $O$ coupe la droite $(B C)$ en $J$.
$c)$ Construire la perpendiculaire à $(A C)$ et passant par $O$ coupe la droite $(A C)$ en $K$.
$5)$ $a)$ Démontrer que : $O I=O J=O K$.
$b)$ En déduire que ( $b_{3}$ ) bissectrice de $\widehat{C}$ passe par $O$.
$c)$ Énoncer la propriété que tu viens de démontrer pour les bissectrices.
$d)$ Que représente le point $O$ pour le triangle $A B C$ ?
$1)$ Construisons un triangle $A B C$ quelconque.
$2)$$ a)$ Construisons la droite $\left(b_{2}\right)$ bissectrice de l’angle $\widehat{A}$; elle coupe $(B C)$ en $A^{\prime}$.
$b)$ Construisons la droite $\left(b_{1}\right)$ bissectrice de l’angle $\widehat{B}$; elle coupe $(A C)$ en $B^{\prime}$.
$3)$ $a)$ $\left(b_{1}\right)$ et $\left(b_{2}\right)$ se coupent en $O$, marquons $O$.
$5)$ $a)$ Démontrons que : $O I=O J=O K$
En effet, on sait que Si un point $M$ appartient à la bissectrice d’un angle alors, il est équidistant des supports des deux côtés de I’angle.
Or, $O \in\left(b_{1}\right)$ bissectrice de l’angle $\widehat{B}$ donc, $O$ est équidistant des supports des deux côtés de l’angle $\widehat{B}$.
C’est-à-dire ; $d(O,(A B)=d(O,(B C)$
Comme, $d(O,(A B)=O I$ et $d(O,(B C)=O J$ alors, on obtient: $O I=O J$
De même, le point $O$ appartient à $\left(b_{2}\right)$ bissectrice de l’angle $\widehat{A}$ donc, $O$ est équidistant des supports des deux côtés de l’angle $\widehat{A}$.
Ce qui signifie : $d(O,(A B))=d(O,(A C))$
Or, $d(O,(A B))=O I$ et $d(O,(A C))=O K$
Par suite, $O I=O K$
Ainsi, $O I=O J$ et $O I=O K$
Ce qui donne alors, $O I=O J=O K$
$b)$ En déduisons que ( $b_{3}$ ) bissectrice de $\widehat{C}$ passe par $O$.
On a : $O I=O J=O K$
Alors, $O J=O K$
Ce qui signifie : $d(O,(B C))=d(O,(A C))$
Donc, le point $O$ est équidistant des supports des deux côtés de l’angle $\widehat{C}$.
Par conséquent, $O$ appartient à la bissectrice $\left(b_{3}\right)$ de l’angle $\widehat{C}$.
D’où, $\left(b_{3}\right)$ passe par $O$.
$c)$ Énonçons la propriété que nous venons de démontrer pour les bissectrices.
Propriété : Dans un triangle, les trois bissectrices sont concourantes (se coupent en un même point).
$d)$ Le point $O$ représente le centre du cercle inscrit dans le triangle $A B C$
Exercice 2:
Construire un triangle $M N P$ tel que : $M N=6 \mathrm{~cm} ; N P=5 \mathrm{~cm}$ et $M P=7 \mathrm{~cm}$.
$1)$ La bissectrice de l’angle $\widehat{M}$ coupe $[N P]$ en $E$.
$2)$ La bissectrice de l’angle $\widehat{N}$ coupe (ME) en $I$.
$3)$ Démontrer que $(I P)$ est la bissectrice de l’angle $\widehat{M P N}$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 3:
$A B C D$ est un parallélogramme de centre $O, P$ est le milieu de $[O B]$. Les droites $(C P)$ et $(D A)$ se coupent en $R$.
$T$ est le symétrique de $R$ par rapport à $P$
Les droites $(R O)$ et ( $D T$ ) se coupent en $M$.
$1)$ Faire une figure complète.
$2)$ Montrer que $(D P)$ est une médiane de $R D T$.
$3)$ Montrer que $D O=\frac{2}{3} D P$
$4)$ Quel est le centre de gravité du triangle $R D T$.
$5)$ Démontrer que $M$ est milieu du segment $[D T]$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 4:
$1)$ Construire un triangle $A B C$ tel que : $A B=5 \mathrm{~cm}, A C=4 \mathrm{~cm}$ et $B C=6 \mathrm{~cm}$.
$I$ et $J$ sont les milieux respectifs de $[A B]$ et $[A C]$.
$2) $ Montrer que les droites $(I J)$ et $(B C)$ sont parallèles puis calculer $I J$.
$3)$ Les demi-droites $[B J]$ et $[C I)$ se coupent en $G$.
$a)$ Que représentent les demi-droites $[B J)$ et $[C I)$ pour le triangle $A B C$ ?
$b)$ Que représente le point $G$ pour le triangle $A B C$ ?
$4)$ Soit $K$ le milieu du segment $[B C]$. Montrer que les points $A, G$ et $K$ sont alignés.
$5)$ On donne $A K=3 \mathrm{~cm}$. Calculer $A G$ et $G K$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 5:
$1)$ Construire un triangle $A B C$ quelconque.
$2)$$a)$ Construire la droite $\left(m_{1}\right)$ médiatrice de $[A B]$.
$b)$ Construire la droite $\left(m_{2}\right)$ médiatrice de $[B C]$.
$2) $$a)$ Les droites $\left(m_{1}\right)$ et ( $m_{2}$ ) se coupent en $O$.
$3)$$ a)$ Démontrer que : $O A=O B=O C$.
$b)$ En déduire que la droite $\left(m_{3}\right)$ médiatrice de $[A C]$ passe par $O$.
$c)$ Énoncer la propriété que tu viens de démontrer pour les médiatrices.
$d)$ Que représente le point $O$ pour le triangle $A B C$ ?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 6:
$1)$ Construire un triangle $A B C$ quelconque.
$2)$$ a)$ Construire $(A M)$ hauteur issue de $A$.
$b) $Construire la droite $(B N)$ hauteur issue de $B$.
$3)$ Les deux droites $(A M)$ et $(B N)$ se coupent en $H$, placer le point $H$.
$4)$$ a)$ Construire la droite $\left(B^{\prime} C^{\prime}\right)$ passant par $A$ et parallèle à $(B C)$.
$b)$ Construire la droite $\left(A^{\prime} C^{\prime}\right)$ passant par $B$ et parallèle à $(A C)$.
$c) $Construire la droite ( $\left.B^{\prime} A^{\prime}\right)$ passant par $C$ et parallèle à $(A B)$.
$5) $Démontrer que : les quadrilatères $A B C B^{\prime} ; B C A C^{\prime}$ et $C A B A^{\prime}$ sont des parallélogrammes.
$6)$$ a)$ Démontrer que $(A H)$ est la médiatrice de $\left[B^{\prime} C^{\prime}\right]$.
$b)$ Démontrer que $(B H)$ est la médiatrice de $\left[A^{\prime} C^{\prime}\right]$.
$c)$ Démontrer que $(C H)$ est la troisième médiatrice du triangle $A^{\prime} B^{\prime} C^{\prime}$.
$7)$$ a)$ Que représentent les médiatrices du triangle $A^{\prime} B^{\prime} C^{\prime}$ ?
$b)$ Énoncer la propriété que tu viens de démontrer pour les hauteurs du triangle.
$c) $ Que représente le point $H$ pour le triangle $A B C$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 7:
Soit $A B C D$ un parallélogramme de centre $H$. La perpendiculaire à $(D B)$ passant par $A$ et la La perpendiculaire à $(A C)$ passant par $B$ se coupent en $G$.
$1)$ Faire une figure.
$2)$ Que représente le point $H$ pour le triangle $A G B$.
$3)$ Montrer que les droites $(G H)$ et $(A B)$ sont perpendiculaires.
$4)$ Montrer que les droites $(G H)$ et $(D C)$ sont perpendiculaires.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 8:
Soit $A B C$ un triangle tel que : $A B=6 \mathrm{~cm} ; A C=7 \mathrm{~cm}$ et $B C=8 \mathrm{~cm}$.
Les points $L, M$ et $N$ sont les milieux respectifs des côtés $[B C],[A B]$ et $[A C]$ d’un triangle $A B C$.
$G$ est le centre de gravité.
$1)$ Faire une figure complète.
$2)$ Démontrer que $M L N A$ est un parallélogramme. Soit $K$ sont centre.
En déduire que : $A K=\frac{1}{2} A L$ puis $K G=\frac{1}{6} A L$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 9:
$1)$ Construis un triangle $A B C$ tel que $A B=14 \mathrm{~cm}, A C=10 \mathrm{~cm}$ et $B C=12 \mathrm{~cm}$.
$2)$ Construis ses médiatrices en rouge, ses médianes en vert, ses hauteurs en bleu et ses bissectrices en noir.
$3)$ Place le point $G$ centre de gravité du triangle, le point $O$ centre du cercle circonscrit, le point $I$ centre du cercle inscrit et le point $H$ orthocentre du triangle.
$4)$ Pour ce triangle $A B C$, construis les cercles circonscrit et inscrit.
$5)$ Trace la droite qui passe par $O$ et $G$.
• Vérifie qu’elle passe par $H$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 10:
Construis le triangle $A B C$ tel que : $A B=3.5 \mathrm{~cm}, \widehat{A B C}=120^{\circ}$ et $B C=5 \mathrm{~cm}$.
$1)$ Trace en bleu la hauteur issue de $A$ et en vert la médiatrice du segment $[B C]$.
$2)$ Démontre que ces deux droites sont parallèles.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Droites remarquable dans le triangle exercices corrigés 2AC
