Droites remarquable dans le triangle exercices corrigés 1AC
Exercice 1:
$1)$ Construire un triangle ABC tel que $\mathrm{AB}=6 \mathrm{~cm}, \mathrm{AC}=13 \mathrm{~cm}$ et $\mathrm{BC}=9 \mathrm{~cm}$.
$2)$ Construire un triangle LMN tel que $\mathrm{LM}=8 \mathrm{~cm}, \mathrm{MN}=5 \mathrm{~cm}$ et $\widehat{\mathrm{LMN}}=100^{\circ}$.
$3)$ Construire un triangle PQR tel que $\mathrm{PQ}=3 \mathrm{~cm}, \widehat{\mathrm{PQR}}=30^{\circ}$ et $\widehat{\mathrm{QPR}}=120^{\circ}$.
$4)$ Peut-on construire un triangle avec pour longueurs des côtés $6 \mathrm{~cm}, 12 \mathrm{~cm}$ et $5,8 \mathrm{~cm}$ ?
$1)$ , $2)$ et $3)$
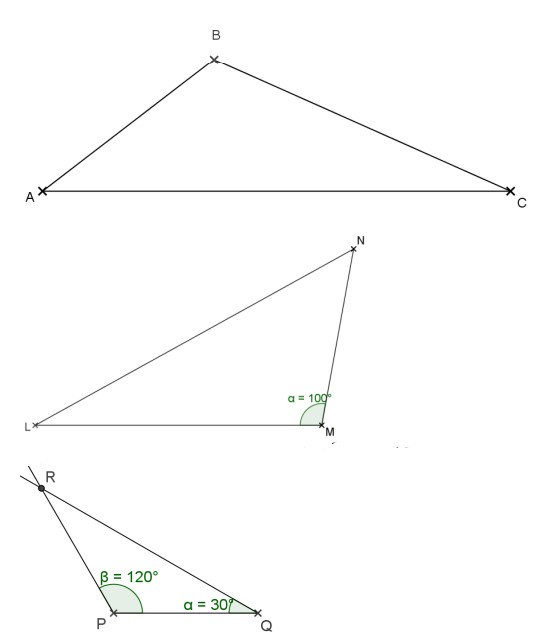
$4)$ Peut-on construire un triangle avec pour longueurs des côtés $6 \mathrm{~cm}, 12 \mathrm{~cm}$ et $5,8 \mathrm{~cm}$ ?
La somme des deux plus petits côtés vaut : $6+5,8=11,8 \mathrm{~cm}$, ce qui est inférieur à la longueur du $3^{\text {ème }}$ côté.
L’inégalité triangulaire n’est pas vérifiée, la construction est impossible.
Exercice 2:
Tracer les trois médianes du triangle ABC ci-contre.
Leur point de concours s’appelle : $\qquad$
Leur point de concours s’appelle : le centre de gravité.
Exercice 3:
Tracer les trois hauteurs du triangle DEF ci-contre (vous ne les prolongerez pas jusqu’à leur point de concours).
Leur point de concours s’appelle : $\qquad$
Leur point de concours s’appelle : l’orthocentre.
Exercice 4:
Tracer les trois médiatrices du triangle GHI ci-contre.
Leur point de concours est : $\qquad$
Leur point de concours est le centre du cercle circonscrit à ce triangle.
Exercice 5:
Sur le cercle ci-contre, placer le point C pour que le cercle soit circonscrit au triangle ABC, sachant que la droite tracée passant par O est la médiatrice du côté [BC]. Justifier :
La médiatrice d’un segment étant une droite perpendiculaire à ce segment en son milieu, le point C appartient à la perpendiculaire à cette droite (d) passant par le point B car $(\mathrm{d}) \perp(\mathrm{BC}) \rightarrow$ on trace cette perpendiculaire.
La médiatrice d’un segment étant l’ensemble des points à égale distance des extrémités de ce segment, O appartenant à cette médiatrice, on a : $\mathrm{OB}=\mathrm{OC}$. Donc le point C appartient au cercle de centre O .
C est le point d’intersection de cette perpendiculaire et du cercle.
Exercice 6:
Dans le triangle ABC , on a tracé les deux hauteurs [AK] et [BH] qui se coupent en un point $O$.
$1)$ Justifier que [CO] est la troisième hauteur du triangle $A B C$.
$2)$ En déduire que $(C O) \perp(A B)$.
Les deux hauteurs [AK] et [BH] se coupent en un point O.
$1)$ On sait que $[\mathrm{AK}]$ et $[\mathrm{BH}]$ sont deux hauteurs se coupant en un point 0 .
Propriété : Les hauteurs d’un triangle se coupent en un même point.
Donc (CO) passant par C et par O est la $3^{\text {ème }}$ hauteur de ce triangle.
$2)$ On sait que ( CO ) est une hauteur du triangle $A B C$.
Propriété : Une hauteur d’un triangle est une droite passant par un
Donc $(C O) \perp(A B)$.
Exercice 7:
Construire le triangle AED dont les deux droites tracées sont deux médiatrices.
Justifier :
La médiatrice d’un segment est une droite perpendiculaire à ce segment en son milieu.
Cet exercice possède donc trois solutions :
Exercice 8:
Construire les cercles circonscrits à ces 2 triangles.
Exercice 9:
Retrouver le centre de ce cercle :
On trace un triangle puis ses médiatrices:
Exercice 10:
Exercice 11:
il y a 3 solutions: FGH, FGH’, FHG’
