Équation d’une droite exercices corrigés pour 3AC
Exercice 1:
Déterminer dans chacun des cas l’équation réduite de la droite $(AB)$ :
$1)$ $A(2;0)$ et $B(4;1)$
$2)$ $A(−2;1)$ et $B(−3;5)$
$3)$$A(\frac{1}{2} ; \frac{2}{3})$ et $B(\frac{7}{6} ; −\frac{1}{5})$
$4)$ $A(−1;5)$ et $B(−1;2)$
$1)$ $A(2 ; 0)$ et $B(4 ; 1)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{1-0}{4-2}=\frac{1}{2}$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=\frac{1}{2} x+b$.
Le point $A(2 ; 0)$ appartient à la droite $(A B)$. Ses coordonnées vérifient donc l’équation précédente
On obtient ainsi : $0=\frac{1}{2} \times 2+b$ soit $0=1+b$ et $b=-1$.
L’équation réduite de $(A B)$ est donc $y=\frac{1}{2} x-1$.
On vérifie avec les coordonnées de $B: \frac{1}{2} x_{B}-1=\frac{1}{2} \times 4-1=2-1=1=y_{B}(:)$
$2)$ $A(-2 ; 1)$ et $B(-3 ; 5)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{5-1}{-3-(-2)}=\frac{4}{-1}=-4$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=-4 x+b$.
Le point $A(-2 ; 1)$ appartient à la droite $(A B)$. Ses coordonnées vérifient donc l’équation précédente
On obtient ainsi : $1=-4 \times(-2)+b$ soit $1=8+b$ et $b=-7$.
L’équation réduite de $(A B)$ est donc $y=-4 x-7$.
On vérifie avec les coordonnées de $B:-4 x_{B}-7=-4 \times(-3)-7=12-7=5=y_{B} \%$
$3)$ $A\left(\frac{1}{2} ; \frac{2}{3}\right)$ et $B\left(\frac{7}{6} ;-\frac{1}{5}\right)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{-\frac{1}{5}-\frac{2}{3}}{\frac{7}{6}-\frac{1}{2}}=\frac{-\frac{13}{15}}{\frac{2}{3}}=-\frac{13}{10}$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=-\frac{13}{10} x+b$.
Le point $A\left(\frac{1}{2} ; \frac{2}{3}\right)$ appartient à la droite $(A B)$.
Ses coordonnées vérifient donc l’équation précédente.
On obtient ainsi : $\frac{2}{3}=-\frac{13}{10} \times \frac{1}{2}+b$ soit $\frac{2}{3}=-\frac{13}{20}+b$ et $b=\frac{79}{60}$.
L’ équation réduite de $(A B)$ est donc $y=-\frac{13}{10} x+\frac{79}{60}$.
On vérifie avec les coordonnées de $B:-\frac{13}{10} x_{B}+\frac{79}{60}=-\frac{13}{10} \times \frac{1}{2}+\frac{79}{60}=-\frac{13}{20}+\frac{79}{60}=\frac{40}{60}=\frac{1}{5}=y_{B}()$
$4)$ $A(-1 ; 5)$ et $B(-1 ; 2)$
$A$ et $B$ ont la même abscisse $-1$ .
Par conséquent l’équation réduite de $(A B)$ est $x=-1$.
Exercice 2:
Déterminer l’équation des droites $(AB)$ , $(BC)$ et $(AC)$ avec $A(2 ; 3)$ , $B(-2 ; 5)$ et $C(2 ; 5)$
• Équation de $(A B)$
Pour $A(2 ; 3) \quad B(-2 ; 5)$
$m=\frac{5-3}{-2-2}=\frac{2}{-4}=-\frac{1}{2}$
l’équation de $(A B)$ est de la forme : $y=\frac{-1}{2} x+p$
$A(2 ; 3) \in(A B)$ donc ses coordonnées vérifient l’équation de $(A B)$
$3=\frac{-1}{2} \times 2+p \Leftrightarrow 3=-1+p \Leftrightarrow p=4$
la droite (AB) a pour équation : $y=\frac{-1}{2} x+4$
• Équation de la droite ( BC )
les points $B(-2 ; 5)$ et $C(2 ; 5)$ ont la même ordonnée inutile de calculer le coefficient directeur (il est nul)
l’équation de la droite (BC) est $y=5$
• Équation de la droite (AC)
les points $A(2 ; 3)$ et $C(2 ; 5)$ ont la même abscisse inutile de calculer le coefficient directeur (il n’existe pas)
l’équation de la droite (AC) est $x=2$
Exercice 3:
Déterminer graphiquement l’équation réduite de chacune des droites suivantes :
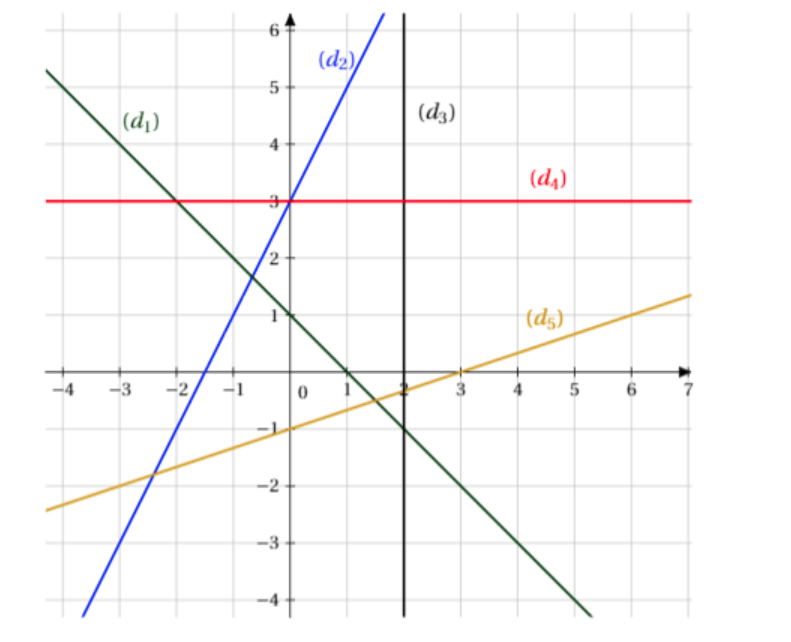
Pour toutes les droites non parallèles à l’axe des ordonnées, les équations des droites seront de la forme $y=a x+b$.
Pour déterminer le coefficient directeur $a$ on lit les déplacements verticaux et horizontaux permettant sur une droite de se déplacer d’un point de la droite situé sur le quadrillage à un autre point de la droite situé également sur le quadrillage (en tenant compte des signes dans les déplacements). $a=\frac{\Delta_{y}}{\Delta_{x}}$
L’ordonnée à l’origine $b$ est l’ordonnée du point de la droite appartenant également à l’axe des ordonnées.
Pour $d_{1}$ : Si on considère les deux points de coordonnées $(0 ; 1)$ et $(2 ;-1)$ (par exemple).
On a $\Delta_{y}=-2$ et $\Delta_{x}=2$ par conséquent $a=\frac{-2}{2}=-1$.
De plus $b=1$.
Par conséquent $d_{1}: y=-x+1$.
$d_{2}: y=2 x+3$
$d_{4}: y=3$
$d_{5}: y=\frac{1}{3} x-1$ car $\Delta_{y}=1$ quand $\Delta_{x}=3$
La droite $d_{3}$ est parallèle à l’axe des ordonnées. Son équation est $x=2$
Exercice 4:
Représenter graphiquement chacune des droites dont l’équation réduite est fournie.
$d_{1}: y=-2 x+3$
$ d_{2}: x=-1$
$d_{3}: y=\frac{4}{5} x-1$
$d_{4}: y=2$
Pour représenter une droite, non parallèle à l’axe des ordonnées, on peut procéder de deux manières :
• On choisit deux abscisses quelconques (suffisamment éloignées pour que le graphique gagne en précision) et on détermine les ordonnées des points de la droite correspondants.
• On place le point de la droite appartenant également à l’axe des ordonnées et on utilise le coefficient directeur pour tracer à partir de ce point la droite.
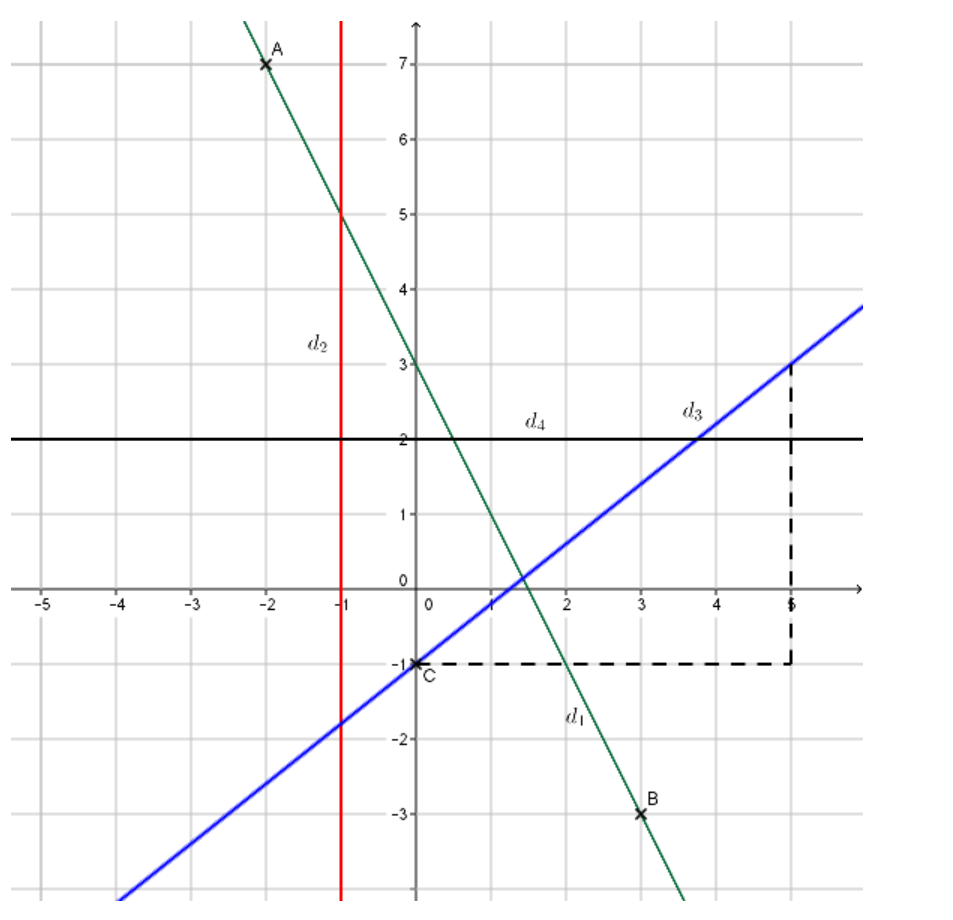
Pour $d_{1}$, on peut choisir, par exemple, $x=−2$ et $x=4$.
Si $x=−2$ alors $y=−2×(−2)+3=7$. La droite passe par le point A de coordonnées $(−2;7)$.
Si $x=3$ alors $y=−2×3+3=−3$. La droite passe par le point $B$ de coordonnées $(3;−3)$.
Pour $d_{3}$, on place le point $C$ de coordonnées $(0;−1)$ et, à partir en se déplaçant de $5$ unités horizontalement vers la droite , on se déplace de $4$ unités verticalement vers le haut; ce qui nous permet de placer un nouveau point et de tracer la droite.
Exercice 5:
Déterminer l’équation réduite des droites dans chacun des cas :
$1)$ La droite $d_{1}$ passe par le point $A(2;3)$ et a pour coefficient directeur $a=−1$.
$2)$ La droite $d_{2}$ passe par le point $ B(−1;2)$ et son ordonnée à l’origine est $−3$.
$3)$ La droite $d_{3}$ passe par le point $C(2;5)$ et est parallèle à la droite d’équation $y=3x−1$.
$1)$ L’équation réduite de $d_{1}$ est donc de la forme $y=−x+b$.
Le point $A(2;3)$ appartient à cette droite, par conséquent ses coordonnées vérifient l’équation de la droite : $3=−2+b$ soit $b=5$.
$d_{1}$ a pour équation réduite $y=−x+5$.
$2)$ L’équation réduite de $d_{2}$ est donc de la forme $y=ax−3$.
Le point $B(−1;2)$ appartient à cette droite, par conséquent ses coordonnées vérifient l’équation de la droite : $2=−a−3$ soit $−a=5$ et donc $a=−5$.
$d_{2}$ a pour équation réduite $y=−5x−3$.
$3)$ Deux droites parallèles ont le même coefficient directeur. L’équation réduite de $d_{3}$ est donc de la forme $y=3x+b$.
Le point $C(2;5)$ appartient à cette droite, par conséquent ses coordonnées vérifient l’équation de la droite : $5=6+b$ soit $b=−1$.
$d_{3}$ a pour équation réduite $y=3x−1$.
Exercice 6:
Indiquer dans chacun des cas si le point appartient à la droite.
$1)$ $A(−2;3) $ et $d_{1}$: $y=−x+1$
$2)$ $B(\sqrt{2};\sqrt{6})$ et $d_{2}$: $y=3x+6$
$3)$ $C(2;1)$ et $d_{3}$: $y=2$.
$1)$ Vérifient est ce que : $y_{A}=-x_{A}+1$.
On a: $-x_{A}+1=−(−2)+1=2+1=3=y_{A}$
Donc $A$ appartient à $d_{1}$.
$2)$ On a: $3x_{B}+6=3\sqrt{2}+6 ≠ \sqrt{6}$
Donc $B$ n’appartient pas à $d_{2}$.
$3)$ L’ordonnée de $C$ n’est pas égale à $2$ donc $C$ n’appartient pas $d_{3}$.
Exercice 7:
On donne les points $A(6;−1)$,$B(2;7)$ et $C(−4;−3)$.
$1)$ Donner une équation réduite des médianes issues de $A$ et de $C$ du triangle $ABC$.
$2)$ Déterminer les coordonnées du centre de gravité du triangle $ABC$.
$1)$ Une médiane est une droite passant par un sommet d’un triangle et le milieu du côté opposé.
On détermine les coordonnées du milieu $A^{\prime}$ de $[B C]:\left(\frac{-4+2}{2} ; \frac{-3+7}{2}\right)=(-1 ; 2)$.
La médiane issue de $A$ passe dont par les points $A(6 ;-1)$ et $A^{\prime}(1 ; 2)$.
Les deux points n’ayant pas la même abscisse, l’équation réduite de cette médiane est de la forme $y=a x+b$.
$a=\frac{2-(-1)}{-1-6}=-\frac{3}{7}$
On obtient ainsi $y=-\frac{3}{7} x+b$.
Les coordonnées de $A$ vérifient cette équation. Donc $-1=-\frac{3}{7} \times 6+b \Leftrightarrow-1=-\frac{18}{7}+b$.
Ainsi $b=-1+\frac{18}{7}=\frac{11}{7}$
L’équation réduite de la médiane issue de $A$ est donc $y=-\frac{3}{7} x+\frac{11}{5}$.
On n’oublie pas de contrôler que les coordonnées de $A^{\prime}$ vérifient cette équation.
On détermine les coordonnées du milieu $C^{\prime}$ de $[A B]:\left(\frac{6+2}{2} ; \frac{-1+7}{2}\right)=(4 ; 3)$.
La médiane issue de $C$ passe dont par les points $C(-4 ;-3)$ et $C^{\prime}(4 ; 3)$.
Les deux points n’ayant pas la même abscisse, l’ équation réduite de cette médiane est de la forme $y=a x+b$.
$a=\frac{3-(-3)}{4-(-4)}=\frac{6}{8}=\frac{3}{4}$
On obtient ainsi $y=\frac{3}{4} x+b$.
Les coordonnées de $C$ vérifient cette équation. Donc $-3=\frac{3}{4} \times(-4)+b \Leftrightarrow-3=-3+b$.
Ainsi $b=0$.
L’équation réduite de la médiane issue de $C$ est donc $y=\frac{3}{4} x$.
On n’oublie pas de contrôler que les coordonnées de $A^{\prime}$ vérifient cette équation.
$2)$ Le centre de gravité $G$ est le point d’intersection des médianes. Ses coordonnées vérifient donc le système :
$\left\{\begin{array}{l}y=-\frac{3}{7} x+\frac{11}{7} \\y=\frac{3}{4} x\end{array}\right.$
$\left\{\begin{array}{l}\frac{3}{4} x=-\frac{3}{7} x+\frac{11}{7} \\y=\frac{3}{4} x\end{array}\right.$
$\left\{\begin{array}{l}\frac{3}{4} x+\frac{3}{7} x=\frac{11}{7} \\y=\frac{3}{4} x\end{array}\right.$
$\left\{\begin{array}{l} \frac{33}{28} x=\frac{11}{7} \\y=\frac{3}{4} x\end{array}\right.$
$\left\{\begin{array}{l}x=\frac{\frac{11}{7}}{\frac{33}{28}} \\ y=\frac{3}{4} x\end{array}\right.$
$\left\{\begin{array}{l}x=\frac{4}{3} \\y=\frac{3}{4} \times \frac{4}{3}\end{array}\right.$
$\left\{\begin{array}{l}x=\frac{4}{3} \\y=1\end{array}\right.$
Ainsi les coordonnees du centre de gravite sont $\left(\frac{4}{3} ; 1\right)$.
Exercice 8:
On donne les points suivants : $A(1;−2)$, $B(4;0)$ , $C(10;4)$ , $D(−2;2)$
$1)$ Les points $A,B,C$ sont-ils alignés?
$2)$ Déterminer l’équation réduite de la parallèle $(Δ)$ à $(AD)$ passant par $B$.
$3)$ Calculer la longueur $AD$.
$4)$ Soit $E$ le point d’intersection de $(Δ)$ et $(CD)$.
Déduire des questions précédentes la longueur $BE$.
$1)$ Pour déterminer si trois points sont alignés on peut :
– Déterminer l’équation réduite de la droite ( $A B$ ) (par exemple) et regarder si $C$ appartient à cette droite.
– Comparer les coefficients directeur de deux droites construites à partir des trois points.
Le coefficient directeur de ( $A B$ ) est $a_{1}=\frac{0-(-2)}{4-1}=\frac{2}{3}$.
Le coefficient directeur de ( $A C$ ) est $a_{2}=\frac{4-(-2)}{10-1}=\frac{6}{9}=\frac{2}{3}$.
Les deux coefficients directeurs étant égaux, les droites $(A B)$ et $(A C)$ sont parallèles. Elles ont le point $A$ en commun.
Elles sont donc confondues et les points $A, B$ et $C$ sont alignés.
$2)$ Le coefficient directeur de ( $A D$ ) est $a_{3}=\frac{2-(-2)}{-2-1}=-\frac{4}{3}$.
La droite $(\Delta)$ étant parallèle à $(A D)$ a le même coefficient directeur.
L’équation réduite de ( $\Delta$ ) est alors de la forme $y=-\frac{4}{3} x+b$.
Le point $B$ appartient à cette droite. Ses coordonnées vérifient l’équation de ( $\Delta$ ).
$0=-\frac{4}{3} \times 4+b \Leftrightarrow b=\frac{16}{3}$.
Une équation de ( $\Delta$ ) est $y=-\frac{4}{3} x+\frac{16}{3}$
$3)$ $A(1 ;-2) \quad D(-2 ; 2)$
$A D=\sqrt{(-2-1)^{2}+(2-(-2))^{2}}$
$=\sqrt{(-3)^{2}+4^{2}}$
$=\sqrt{9+16}$
$ =\sqrt{25} $
$ =5$
$4)$ $C(10 ; 4) \quad D(-2 ; 2)$
L’équation réduite de ( $C D$ ) est de la forme $y=a x+b$.
Son coefficient directeur est $a=\frac{2-4}{-2-10}=\frac{-2}{-12}=\frac{1}{6}$
L’équation réduite de ( $C D$ ) est de la forme $y=\frac{1}{6} x+b$
$C$ appartient à cette droite. Ses coordonnées vérifient donc l’équation de cette droite : $4=\frac{1}{6} \times 10+b \Leftrightarrow 4-\frac{5}{3}=b \Leftrightarrow b=\frac{7}{3}$.
L’équation réduite de $(C D)$ est donc $y=\frac{1}{6} x+\frac{7}{3}$.
On contrôle que les coordonnées de $D$ vérifient cette équation
Les coordonnées du point d’intersection de $(C D)$ et $(\Delta)$ vérifient le système suivant :
$\left\{\begin{array}{l}y=\frac{1}{6} x+\frac{7}{3} \\y=-\frac{4}{3} x+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}-\frac{4}{3} x+\frac{16}{3}=\frac{1}{6} x+\frac{7}{3} \\y=-\frac{4}{3} x+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}-\frac{4}{3} x-\frac{1}{6} x=-\frac{16}{3}+\frac{7}{3} \\y=-\frac{4}{3} x+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}-\frac{3}{2} x=-3 \\y=-\frac{4}{3} x+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}x=\frac{-3}{-\frac{3}{2}} \\y=-\frac{4}{3} x+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}x=2 \\y=-\frac{4}{3} \times 2+\frac{16}{3}\end{array}\right.$
$\left\{\begin{array}{l}x=2 \\y=\frac{8}{3}\end{array}\right.$
$E$ a pour coordonnées $\left(2 ; \frac{8}{3}\right)$.
Par conséquent :
$B E=\sqrt{(2-4)^{2}+\left(\frac{8}{3}-0\right)^{2}}$
$=\sqrt{4+\frac{64}{9}}$
$=\sqrt{\frac{100}{9}}$
$=\frac{10}{3}$
Exercice 9:
On donne les points $A(2;3) , B(6;0) , C(0;−4)$.
$1)$ Démontrer que les points $A,B,C$ forment un triangle.
$2)$ Calculer les coordonnées du milieu $I$ du segment $[BC]$.
$3)$ Déterminer l’équation réduite de la droite $(d)$ passant par $B$ et parallèle à la médiane issue de $A$.
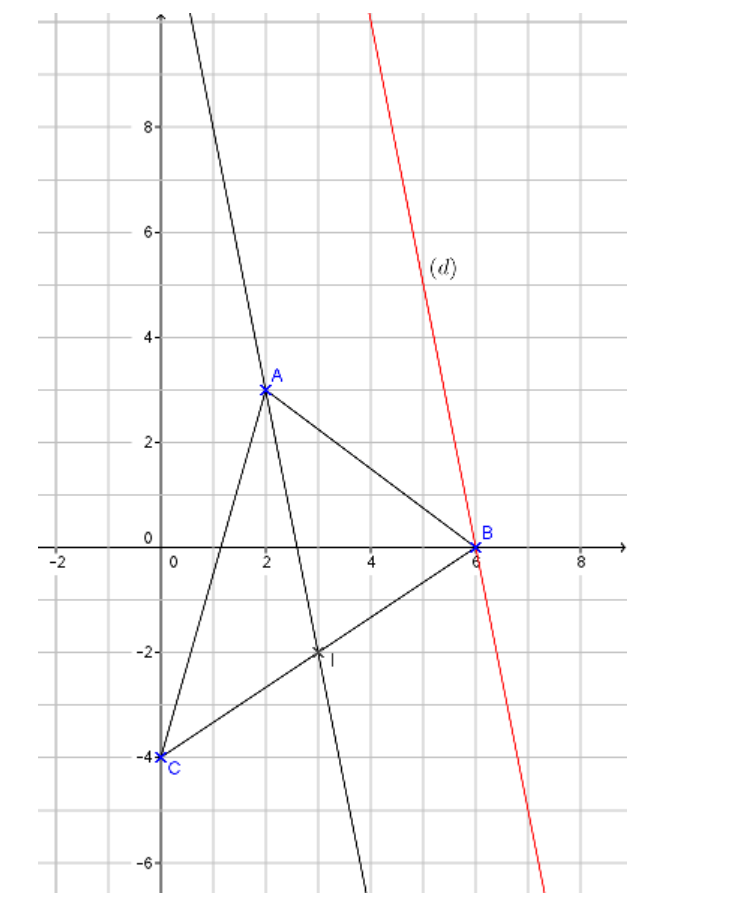
$4)$ Vérifier les réponses précédentes à l’aide d’un graphique.
$1)$ On vérifie donc que les points ne sont pas alignés.
Le coefficient directeur de $(A B)$ est $\frac{0-3}{6-2}=-\frac{3}{4}$.
Le coefficient directeur de $(A C)$ est $\frac{-4-3}{0-2}=\frac{7}{2}$.
Les coefficients directeurs ne sont pas égaux. Les points $A, B$ et $C$ ne sont donc pas alignés et forment bien un triangle.
$2)$ Les coordonnées de $I$ sont $\left(\frac{6+0}{2} ; \frac{0-4}{2}\right)=(3 ;-2)$.
3. La médiane issue de $A$ passe également par $I$.
$A$ et $I$ n’ont pas la même abscisse; l’équation réduite de $(A I)$ est donc de la forme $y=a x+b$.
$a=\frac{-2-3}{3-2}=-5$.
L’équation réduite de $(d)$ est donc de la forme $y=-5 x+c$.
$B$ appartient à cette droite. donc $0=-5 \times 6+c \Leftrightarrow b=30$
$(d)$ a pour équation réduite $y=-5 x+30$.
$4)$
Exercice 10:
$1)$ $d: y=5 x-3$ et $d^{\prime}: y=-5 x+3$
$2)$ $d: y=2 x-5$ et $d^{\prime}: y=2 x+3$
$3)$ $d: y=-4-x$ et $d^{\prime}: y=-4 x-1$
$4)$ $d: y=\frac{1}{3} x+2$ et $d^{\prime}: y=0,33 x$
$1)$ Non car les coefficients directeurs sont différents $(5 \neq-5)$.
$2)$ Oui car les coefficients directeurs sont égaux.
$3)$Non car les coefficients directeurs sont différents $(-1 \neq-4)$.
$4)$ Non car les coefficients directeurs sont différents ( $\frac{1}{3} \neq 0,33$ ).
Exercice 11:
Le plan muni d’un repère.
On considère des droites $ d_{1}$ et $ d_{2}$ données par leurs équations.
Dans chaque cas, déterminer si $ d_{1}$et $ d_{2}$ sont parallèles, confondues ou sécantes.
$1)$$ d_{1}$ :$ y = 3x -2$ ; $ d_{2}$ : $y = 3x + 32$
$2)$ $ d_{1}$ : $x – 3y + 3 =0$ ; $ d_{2}$ : $−\frac{1}{3}x + y -1 = 0$
$3)$ $ d_{1}$ : $y = – 6$ ; $ d_{2}$ :$ x = – 6$
$1)$
$ d_{1}$ et $ d_{2}$ ont le même coefficient directeur $3$ et des ordonnées à l’origine différentes $– 2$ et $3/2$.
$ d_{1}$ et $ d_{2}$ sont parallèles.
$2)$
$ d_{1}$ : $x – 3y + 3 =0$ équivaut à : $y =\frac{1}{3}x+1$
$ d_{2}$ : $−\frac{1}{3}x + y -1 = 0$ équivaut à : $y =\frac{1}{3}x+1$
Même équation, donc $ d_{1}$ et $ d_{2}$ sont confondues
$3)$
$ d_{1}$ est parallèle à l’axe des abscisses. $ d_{2}$ est parallèle à l’axe des ordonnées donc $ d_{1}$ et $ d_{2}$ sont sécantes.
Exercice 12:
Parmi les droites données dire quelles sont celles qui sont perpendiculaires:
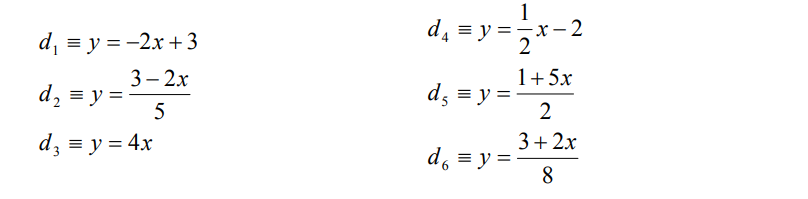
• NB: si $a1×a2 = -1$ alors les droites sont perpendiculaires
• $ d_{1}$ et $ d_{2}$ sont perpendiculaires, car : $-2×\frac{1}{2} = -1$
• $ d_{2}$ et $ d_{5}$ sont perpendiculaires, car : $(-\frac{2}{5})×(\frac{5}{2}) = -1$
Exercice 13:
Dans le plan rapporté à une repère orthonormé on considère les points : $A(1 ;-4),B( 3;4),C(0 ;2)$ et $D(2 ;0)$
$1)$ Déterminons l’équation réduite de la droite $(AB)$.
$2)$ Parmi les points $C$ et $D$ déterminons le point qui appartient et le point qui n’appartient pas à la droite $(AB)$
$3)$ Déterminons l’équation réduite de la droite $(d)$ qui passe par le point $C$ et qui est parallèle à v(AB)$ .
$4)$ Déterminons l’équation réduite de la droite $(d’)$ qui passe par le point $C$ et qui est perpendiculaire à $(AB)$ .
$5)$ Déterminons l’équation réduite de la médiatrice $(Δ)$ du segment $[AB]$.
$1)$ L’équation réduite de la droite $(AB)$ s’écrit sous la forme : $y=a x+b$
• Déterminons $a$ :
$a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{4-(-4)}{3-1}=\frac{4+4}{2}=\frac{8}{2}=4$
$y=4 x+b$
• Déterminons $b$ :
$B( 3;4)∈(AB)$ alors : $y_{B}=a x_{B}+b$
$4=4 \times 3+b$ Signifié que $4=12+b$ d’où $4-12=$
Finalement l’équation réduite de la droite $(AB)$ est : $y=4 x-8$
$2)$
* Pour $\mathrm{C}(0 ; 2)$ on a $x_{C}=0$ alors si on remplace $x$ par $0$ dans l’équation réduite de la droite $( AB )v on trouve :
$y=4 \times 0-8=0-8=-8 \neq 2=y_{C}$
D’où le point $C(0 ; 2)$ n’appartient pas à la droite $(AB)$.
* Pour $\mathrm{D}(2 ; 0)$ on a $y_{D}=0$ alors si on remplace $y$ par $0$ dans l’équation réduite de la droite $(A B)$ on trouve :
$0=4 \times x-8$ alors $0+8=4 x$ signifié $\frac{8}{4}=\frac{4 \mathrm{x}}{4}$ d’où $x=2=x_{D}$
D’où le point $\mathrm{D}(2 ; 0)$ appartient pas à la droite $(\mathrm{AB}$.
$3)$ L’équation réduite de la droite (d) s’écrit sous la forme : $y=a^{\prime} x+b^{\prime}$
• Déterminons $a^{\prime}$:
Comme $(d) / /(A B)$ alors ils ont même coefficient directeur d’ où $a^{\prime}=a=4$
• Déterminons $b^{\prime}$ :
$C(0 ; 2) \in(d)$ alors $y_{C}=4 x_{C}+b^{\prime}$
$y=4 x+b^{\prime}$
$2=4 \times 0+b^{\prime}$ d’où $b^{\prime}=2$
Finalement l’équation réduite de la droite $(AB)$ est : $y=4 x+2$
$4)$ L’équation réduite de la droite ( $\mathrm{d}^{\prime}$ ) s’écrit sous la forme : $y=a^{\prime \prime} x+b^{\prime \prime}$
• Déterminons $a^{\prime \prime}$
Comme ( $d^{\prime}$ ) et (AB) sont perpendiculaire alors le produit de leur coefficients directeurs est égale à -1
C’est-à-dire a $\times \mathrm{a}^{\prime \prime}=-1$ signifie que $4 \times \mathrm{a}^{\prime \prime}=-1$
D’où $\frac{4 a^{\prime \prime}}{4}=\frac{-1}{4}$
Finalement $\mathbf{a}^{\prime \prime}=\frac{-1}{4}$
$y=\frac{-1}{4} x+b^{\prime \prime}$
• Déterminons $\mathbf{b}^{\prime \prime}$
$\mathrm{C}(0 ; 2) \in(\mathrm{d})$ alors $y_{C}=\frac{-1}{4} x_{C}+b^{\prime \prime}$
$2=\frac{-1}{4} \times 0+b^{\prime \prime}$ d’où $b^{\prime \prime}=2$
Finalement l’équation réduite de la droite ( $\mathrm{d}^{\prime}$ ) est : $y=\frac{-1}{4} x+2$
$5)$ L’équation réduite de la droite $(\Delta)$ s’écrit sous la forme : $y=m x+p$
• Déterminons $m$
On sait que la médiatrice d’un segment c’est la droite qui passe perpendiculairement à son milieu alors : $(\Delta) \perp(A B)$ et comme $\left(d^{\prime}\right) \perp(A B)$
Alors $(\Delta) / /\left(d^{\prime}\right)$
D’où : $m=a^{\prime \prime}=\frac{-1}{4}$
$y=\frac{-1}{4} x+p$
• Déterminons $p$
On sait que ( $\Delta$ ) passe par le point $I$ le milieu de $[AB]$.
Calculons les coordonnées du point |:
$I\left(\frac{\mathrm{x}_{\mathrm{A}}+\mathrm{x}_{\mathrm{B}}}{2} ; \frac{\mathrm{y}_{\mathrm{A}}+\mathrm{y}_{\mathrm{B}}}{2}\right)$
alors $I\left(\frac{1+3}{2} \frac{-4+4}{2}\right)$ d’où $\mathrm{I}(2 ; 0)$
(On remarque que le point $D$ est le milieu de $[AB]$).
$\mathrm{D}(2 ; 0) €(\Delta)$ alors $y_{D}=\frac{-1}{4} x_{D}+p$
$0=\frac{-1}{4} \times 2+p$
Signifié que $-p=\frac{-1}{2}$
D’où $p=\frac{1}{2}$
Finalement l’équation réduite de la droite (d’) est : $y=\frac{\mathbf{- 1}}{\mathbf{4}} x+2$
Équation d’une droite exercices corrigés pour 3AC
