Équations et inéquations exercices corrigés pour 3AC biof

Équations et inéquations exercices corrigés

Exercice 1:

$1)$ Résoudre les équations suivantes :

$3 - 2 x - 3 - x = 5 - x + 18$

$7 + 5 x = 7 x - 13$

$2 x = 13 - 4 x$

$2)$ Résoudre les équations suivantes :

$3 (x + 1) - (x - 9) + (x + 3) = (x + 4) + (x + 2) - (11 - x)$

$6 (x - 3) - 3 (x - 2) = 4 (3 - x) + 5$

$4 (x - 4) + 25 (x + 1) = 10 (2 x + 3) + 15$

$7 (2 x - 5) - 5 (3 x + 1) = 6 (x - 4) - 7$

$(x - 1) (x + 3) = (x + 4) (x - 2)$

$(x + 3) (x + 5) = (x + 1) (x + 9)$

$3 (x - 3) = (x - 4) (x + 1) - (x - 5) (x - 1)$

Correction de l’exercice 1

$1)$ Résoudre les équations suivantes :

• $3 - 2 x - 3 - x = 5 - x + 18$

$- 2 x - x + x = 5 + 18 + 3 - 3$

$- 2 x = 23$

$x = \frac{23}{- 2}$

$x = - \frac{23}{2}$

$s = {- \frac{23}{2}}$

• $7 + 5 x = 7 x - 13$

$5 x - 7 x = - 13 - 7$

$- 2 x = - 20$

$x = \frac{- 20}{- 2}$

$x = 10$

$s = {10}$

• $2 x = 13 - 4 x$

$2 x + 4 x = 13$

$6 x = 13$

$x = \frac{13}{6}$

$s = {\frac{13}{6}}$

$2)$ Résoudre les équations suivantes :

• $3 (x + 1) - (x - 9) + (x + 3) = (x + 4) + (x + 2) - (11 - x)$

$3 x + 3 - x + 9 + x + 3 = x + 4 + x + 2 - 11 + x$

$3 x + 15 = 3 x - 5$

$3 x - 3 x = - 5 - 15$

$0 x = - 20$

$s = \emptyset$

L’équation n’admet pas de solution.

• $6 (x - 3) - 3 (x - 2) = 4 (3 - x) + 5$

$6 x - 18 - 3 x + 6 = 12 - 4 x + 5$

$3 x - 12 = - 4 x + 17$

$3 x + 4 x = 17 + 12$

$7 x = 29$

$x = \frac{29}{7}$

$s = {\frac{29}{7}}$

• $4 (x - 4) + 25 (x + 1) = 10 (2 x + 3) + 15$

$4 x - 16 + 25 x + 25 = 20 x + 30 + 15$

$29 x + 9 = 20 x + 45$

$29 x - 20 x = 45 - 9$

$9 x = 36$

$x = \frac{36}{9}$

$x = 4$

$s = {4}$

• $7 (2 x - 5) - 5 (3 x + 1) = 6 (x - 4) - 7$

$14 x - 35 - 15 x - 5 = 6 x - 24 - 7$

$- x - 40 = 6 x - 31$

$- x - 6 x = - 31 + 40$

$- 7 x = 9$

$x = \frac{9}{- 7}$

$x = - \frac{9}{7}$

$s = {- \frac{9}{7}}$

• $(x - 1) (x + 3) = (x + 4) (x - 2)$

$x^{2} + 3 x - x - 3 = x^{2} - 2 x + 4 x - 8$

$x^{2} + 2 x - 3 = x^{2} + 2 x - 8$

$x^{2} - x^{2} + 2 x - 2 x = - 8 + 3$

$0 x = - 5$

$s = \emptyset$

L’équation n’admet pas de solution.

• $(x + 3) (x + 5) = (x + 1) (x + 9)$

$x^{2} + 5 x + 3 x + 15 = x^{2} + 9 x + x + 9$

$x^{2} + 8 x + 15 = x^{2} + 10 x + 9$

$x^{2} - x^{2} + 8 x - 10 x = 9 - 15$

$- 2 x = - 6$

$x = \frac{- 6}{- 2}$

$x = 3$

$s = {3}$

• $3 (x - 3) = (x - 4) (x + 1) - (x - 5) (x - 1)$

$3 x - 9 = x^{2} + x - 4 x - 4 - (x^{2} - x - 5 x + 5)$

$3 x - 9 = x^{2} - 3 x - 4 - x^{2} + 6 x - 5$

$3 x - 9 = 3 x - 9$

$3 x - 3 x = - 9 - 9$

$0 x = 0$

$s = P$

L’équation admet une infinité de solutions.

Exercice 2:

Résoudre les équations suivantes :

$a)$ $\frac{2 x}{3} + 5 = \frac{2 x}{5} + 6$

$b)$ $\frac{3 x}{5} - \frac{2 x - 7}{15} + \frac{x}{3} = 0$

$c)$ $\frac{3 x - 1}{2} - \frac{5 x - 2}{3} + \frac{7 x - 3}{4} = \frac{24}{5}$

$d)$ $\frac{5 x + 1}{5} - \frac{3 x - 1}{4} = \frac{2 (4 x + 1)}{5}$

$e)$ $\frac{2 x + 1}{3} - \frac{x - 1}{5} = \frac{7 x - 12}{15}$

Correction de l’exercice 2

$a)$ $\frac{2 x}{3} + 5 = \frac{2 x}{5} + 6$

$\frac{2 x \times 5}{15} + \frac{5 \times 15}{15} = \frac{2 x \times 3}{15} + \frac{6 \times 15}{15}$

$10 x + 75 = 6 x + 90$

$10 x - 6 x = 90 - 75$

$4 x = 15$

$x = \frac{15}{4}$

$s = {\frac{15}{4}}$

$b)$ $\frac{3 x}{5} - \frac{2 x - 7}{15} + \frac{x}{3} = 0$

$\frac{3 x \times 3}{15} - \frac{2 x - 7}{15} + \frac{5 \times x}{15} = 0$

$9 x - (2 x - 7) + 5 x = 0$

$9 x - 2 x + 7 + 5 x = 0$

$12 x = - 7$

$x = - \frac{7}{12}$

$s = {- \frac{7}{12}}$

$c)$ $\frac{3 x - 1}{2} - \frac{5 x - 2}{3} + \frac{7 x - 3}{4} = \frac{24}{5}$

$\frac{30 \times (3 x - 1)}{60} - \frac{20 \times (5 x - 2)}{60} + \frac{15 \times (7 x - 3)}{60} = \frac{24 \times 12}{60}$

$30 (3 x - 1) - 20 (5 x - 2) + 15 (7 x - 3) = 288$

$90 x - 30 - 100 x + 40 + 105 x - 45 = 288$

$95 x = 288 + 30 + 45 - 40$

$95 x = 323$

$x = \frac{323}{95}$

$s = {\frac{323}{95}}$

$d)$ $\frac{5 x + 1}{5} - \frac{3 x - 1}{4} = \frac{2 (4 x + 1)}{5}$

$\frac{4 \times (5 x + 1)}{20} - \frac{5 \times (3 x - 1)}{20} = \frac{4 \times 2 (4 x + 1)}{20}$

$4 (5 x + 1) - 5 (3 x - 1) = 8 (4 x + 1)$

$20 x + 4 - 15 x + 5 = 32 x + 8$

$5 x + 9 = 32 x + 8$

$5 x - 32 x = 8 - 9$

$- 27 x = - 1$

$x = \frac{- 1}{- 27}$

$x = \frac{1}{27}$

$S = {\frac{1}{27}}$

$e)$ $\frac{2 x + 1}{3} - \frac{x - 1}{5} = \frac{7 x - 12}{15}$

$\frac{5 \times (2 x + 1)}{15} - \frac{3 \times (x - 1)}{15} = \frac{7 x - 12}{15}$

$5 (2 x + 1) - 3 (x - 1) = 7 x - 12$

$10 x + 5 - 3 x + 3 = 7 x - 12$

$7 x + 8 = 7 x - 12$

$7 x - 7 x = - 12 - 8$

$0 x = - 20$

$s = \emptyset$

Exercice 3:

Compléter les pointillés :

$a)$ $(2 x + 5) (3 x + 1) = 0$
signifie que $\dots \dots \dots \dots \dots \dots = 0$ ou $\dots \dots \dots \dots \dots \dots = 0$

$b)$ $6 x (- x + 4) = 0$
signifie que $\dots \dots \dots \dots \dots \dots = 0$ ou $\dots \dots \dots \dots \dots . . = 0$

$c)$ $(9 - 4 x) (3 + 1) = 0$
signifie que ………………………………………………..

$d)$ $5 x (- 6 + x) (7 x + 2) = 0$
signifie que ………………………………………………..

$e)$ $(4 - 3 x) (x - 7) (6 + 5 x) = 0$
signifie que ………………………………………………..

Correction de l’exercice 3

$a)$ $(2 x + 5) (3 x + 1) = 0$
signifie que $2 x + 5 = 0$ ou $3 x + 1 = 0$

$b)$ $6 x (- x + 4) = 0$
signifie que $6 x = 0$ ou $- x + 4 = 0$

$c)$ $(9 – 4x)(3 + 1) = 0$
signifie que $9 - 4 x = 0$ bien sûr $3 + 1 = 4$

$d)$ $5 x (- 6 + x) (7 x + 2) = 0$
signifie que $5 x = 0$ ou $- 6 + x = 0$ ou $7 x + 2 = 0$

$e)$ $(4 - 3 x) (x - 7) (6 + 5 x) = 0$
signifie que $4 - 3 x = 0$ ou $x - 7 = 0$ ou $6 + 5 x = 0$

Exercice 4:

Résoudre les équations suivantes :

$a)$ $(x + 5) (x - 3) = 0$

$b)$ $(4 x - 1) (6 x + 5) = 0$

$c)$ $(- 8 x + 5) (- 2 - 3 x) = 0$

$d)$ $(3 x + 4) (2 - 5 x) = 0$

$e)$ $(5 + 3 x) (7 - x) = 0$

$f)$ $3 x (7 + 8 x) = 0$

$g)$ $- 8 x (- 3 - 6 x) = 0$

$h)$ $(4 x - 2) (2 - x) = 0$

Correction de l’exercice 4

$a)$ $(x + 5) (x - 3) = 0$

signifie que :

$x + 5 = 0 ou x - 3 = 0$

$x = - 5 ou x = 3$

Les solutions de l’équation sont : $- 5 et 3$

$b)$ $(4 x - 1) (6 x + 5) = 0$ signifie que :

$4 x - 1 = 0 ou 6 x + 5 = 0$

$4 x = 1 ou 6 x = - 5$

$x = \frac{1}{4} ou x = - \frac{5}{6}$

Les solutions de l’équation sont : $\frac{1}{4} et - \frac{5}{6}$

$c)$ $(- 8 x + 5) (- 2 - 3 x) = 0$

signifie que :

$- 8 x + 5 = 0 ou - 2 - 3 x = 0$

$- 8 x = - 5 ou - 3 x = 2$

$x = \frac{5}{8} ou x = - \frac{2}{3}$

Les solutions de l’équation sont : $\frac{5}{8} et - \frac{2}{3}$

$d)$ $(3 x + 4) (2 - 5 x) = 0$

signifie que : $3 x + 4 = 0 ou 2 - 5 x = 0$

$3 x = - 4 ou - 5 x = - 2$

$x = - \frac{4}{3} ou x = \frac{2}{5}$

Les solutions de l’équation sont : $- \frac{4}{3} et \frac{2}{5}$

$e)$ $(5 + 3 x) (7 - x) = 0$

signifie que : $5 + 3 x = 0 ou 7 - x = 0$

$3 x = - 5 ou - x = - 7$

$x = - \frac{5}{3} ou x = 7$

Les solutions de l’équation sont : $- \frac{5}{3} et 7$

$f)$ $3 x (7 + 8 x) = 0$ signifie que :

$3 x = 0 ou 7 + 8 x = 0$

$x = 0 ou 8 x = - 7$

$x = 0 ou x = - \frac{7}{8}$

Les solutions de l’équation sont: $0 et - \frac{7}{8}$

$g)$ $- 8 x (- 3 - 6 x) = 0$ signifie que :

$- 8 x = 0 ou - 3 - 6 x = 0$

$x = 0 ou - 6 x = 3$

$x = 0 ou x = - \frac{1}{2}$

Les solutions de l’équation sont : $0$ et $- \frac{1}{2}$

$h)$ $(4 x - 2) (2 - x) = 0$ signifie que :

$4 x - 2 = 0 ou 2 - x = 0$

$4 x = 2 ou - x = - 2$

$x = \frac{1}{2} ou x = 2$

Les solutions de l’équation sont : $\frac{1}{2} et 2$

Exercice 5:

Résoudre les équations suivantes :

$(x + 5)^{2} + (x + 5) (x - 1) = 0$

$(2 x + 3)^{2} - 4 = 0$

$(7 t + 11)^{2} = 36$

$x^{2} - 2 \times x \times 1 + 1^{2} = 0$

$x^{2} = 64$

$x^{2} + 81 = 0$

$9 x^{2} - 25 = 0$

$x^{2} = 180$

$(5 x + 8) (4 x + 5) (x - 7) = 0$

$(3 x - 1) (3 x + 1) - (3 x - 1)^{2} = 0$

$9 x^{2} + 6 x + 1 = 0$

$x^{2} - 5 = 20$

Correction de l’exercice 5

$(x + 5)^{2} + (x + 5) (x - 1) = 0$
$(x + 5) \times (x + 5) + (x + 5) \times (x - 1) = 0$
$(x + 5) \times [(x + 5) + (x - 1)] = 0$
$(x + 5) \times (2 x + 4) = 0$
$Si a \times b = 0 alors a = 0 ou b = 0$
$x + 5 = 0 ou 2 x + 4 = 0$
$x = - 5 ou x = \frac{- 4}{2} = - 2$

$S = {- 5; - 2}$

$(2 x + 3)^{2} - 4 = 0$
$(2 x + 3)^{2} - 2^{2} = 0$
$[(2 x + 3) - 2] [(2 x + 3) + 2] = 0$
$(2 x + 1) (2 x + 5) = 0$
$Si a \times b = 0 alors a = 0 ou b = 0$
$2 x + 1 = 0 ou 2 x + 5 = 0$
$2 x = - 1 ou 2 x = - 5$
$x = - \frac{1}{2} ou x = - \frac{5}{2}$
$x = - 0, 5 ou x = - 2, 5$

$S = {- 2, 5; - 0, 5}$

$(7 t + 11)^{2} = 36$
$(7 t + 11)^{2} - 36 = 0$
$(7 t + 11)^{2} - 6^{2} = 0$
$[(7 t + 11) - 6] [(7 t + 11) + 6] = 0$
$(7 t + 5) (7 t + 17) = 0$
$Si a \times b = 0 alors a = 0 ou b = 0$
$7 t + 5 = 0 ou 7 t + 17 = 0$
$7 t = - 5 ou 7 t = - 17$
$t = \frac{- 5}{7} ou t = \frac{- 17}{7}$

$S = {- \frac{5}{7}; - \frac{17}{7}}$

$x^{2} - 2 \times x \times 1 + 1^{2} = 0$
$(x - 1)^{2} = 0$
Si $a^{2} = 0$ alors $a = 0$
$x - 1 = 0$
$x = 1$
$S = {1}$

$x^{2} = 64$
$64 > 0$ donc $x = \sqrt{64} = 8$ ou $x = - \sqrt{64} = - 8 S = {8; - 8}$

$x^{2} + 81 = 0$
$x^{2} = - 81$
$- 81 < 0$ donc l’équation n’admet pas de solution $S = \emptyset$

$9 x^{2} - 25 = 0$
$9 x^{2} = 25$
$x^{2} = \frac{25}{9}$
$\frac{25}{9} > 0$ donc $x = \sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}$ ou $x = - \sqrt{\frac{25}{9}} = - \frac{5}{3} S = {\frac{5}{3}; - \frac{5}{3}}$

$x^{2} = 180$
$180 > 0$ donc $x = \sqrt{180} = \sqrt{36 \times 5} = \sqrt{36} \times \sqrt{5} = 6 \sqrt{5}$ ou $x = - 6 \sqrt{5}$
$S = {6 \sqrt{5}; - 6 \sqrt{5}}$

$(5 x + 8) (4 x + 5) (x - 7) = 0$

$5 x + 8 = 0$ ou $4 x + 5 = 0$ ou $x - 7 = 0$
$x = - \frac{8}{5}$ ou $x = - \frac{5}{4}$ ou $x = 7$
Les solutions de cette équation sont $- \frac{5}{4}; \frac{8}{5}$ et 7 .

$(3 x - 1) (3 x + 1) - (3 x - 1)^{2} = 0$
$(3 x - 1) [(3 x + 1) - (3 x - 1)] = 0$
$(3 x - 1) \times 2 = 0$
$3 x - 1 = 0$
$x = \frac{1}{3}$
La solution de cette équation est $\frac{1}{3}$ .

$9 x^{2} + 6 x + 1 = 0$
$(3 x + 1)^{2} = 0$
$x = - \frac{1}{3}$
La solution de cette équation est $- \frac{1}{3}$ .

$x^{2} - 5 = 20$ $\to x^{2} = 25 \to x = - 5$ ou $x = 5$
Les solutions de cette équation sont $- 5$ et $5$ .

Exercice 6:

$1)$ Tester (mentalement) les 4 nombres pour chaque inéquation et cocher les solutions :

$2)$ Tester l’inéquation $4 x - 3 > 9 - 2 x$ pour les différentes valeurs de $x$ .

• Si $x = 1$

• Si $x = 2$

• Si $x = 3$

$3)$ Tester l’inéquation $4 - 3 x \leq 4 x + 18$ pour les différentes valeurs de $x$ .

• Si $x = 2$

• Si $x = - 5$

• Si $x = - 2$

Correction de l’exercice 6

$1)$ Tester (mentalement) les 4 nombres pour chaque inéquation et cocher les solutions :

$2)$ Tester l’inéquation $4 x - 3 > 9 - 2 x$ pour les différentes valeurs de $x$ .

• Si $x = 1$

D’une part:

$4 x - 3 = 4 \times 1 - 3 = 4 - 3 = 1$

D’autre part :

$9 - 2 x = 9 - 2 \times 2 = 9 - 2 = 7$

Puisque $1 < 7$ , alors $1$ n’est pas une solution de l’inéquation

• Si $x = 2$

D’une part:

$4 x - 3 = 4 \times 2 - 3 = 8 - 3 = 5$

D’autre part :

$9 - 2 x = 9 - 2 \times 2 = 9 - 4 = 5$

Puisque $5 = 5$ , alors $2$ n’est pas une solution de l’inéquation

• Si $x = 3$

D’une part:

$4 x - 3 = 4 \times 3 - 3 = 12 - 3 = 9$

D’autre part :

$9 - 2 x = 9 - 2 \times 3 = 9 - 6 = 3$

Puisque $9 > 3$ , alors $3$ est une solution de l’inéquation

$3)$ Tester l’inéquation $4 - 3 x \leq 4 x + 18$ pour les différentes valeurs de $x$ .

• Si $x = 2$

D’une part:

$4 - 3 x = 4 - 3 \times 2 = 4 - 6 = - 2$

D’autre part :

$4 x + 18 = 4 \times 2 + 18 = 8 + 18 = 26$

Puisque $- 2 < 26$ , alors $2$ est une solution de l’inéquation

• Si $x = - 5$

D’une part:

$4 - 3 x = 4 - 3 \times (- 5) = 4 + 15 = 19$

D’autre part :

$4 x + 18 = 4 \times (- 5) + 18 = - 20 + 18 = - 2$

Puisque $19 > - 2$ , alors $2$ n’est pas une solution de l’inéquation

• Si $x = - 2$

D’une part:

$4 - 3 x = 4 - 3 \times (- 2) = 4 + 6 = 10$

D’autre part :

$4 x + 18 = 4 \times (- 2) + 18 = - 8 + 18 = 10$

Puisque $10 \leq 10$ , alors $- 2$ n’est pas une solution de l’inéquation

Exercice 7:

$1)$ Résoudre les inéquations suivantes :

$5 x > - 2$

$7 x < - 3$

$x + 2 \geq 5$

$x - 5 \leq 7$

$- 2 x > 5$

$3 x \leq - 4$

$- 3 x \geq - 12$

$28 \leq - 7 x$

$42 < 6 x$

$- 5 x \geq - 35$

$2)$ Résoudre les inéquations suivantes :

$3 x + 5 > - 2$

$7 x + 5 < - 3$

$4 - 3 x \geq 2$

$8 x + 3 \leq 6$

$- 3 > - 5 x + 7$

$8 - 7 x \leq 4$

$7 x + 2 > x + 6$

$- 4 x + 7 \leq 5 - x$

Correction de l’exercice 7

$1)$ Résoudre les inéquations suivantes :

$5 x > - 2$ $\Rightarrow$ $x > - \frac{2}{5}$

$7 x < - 3$ $\Rightarrow$ $x < - \frac{3}{7}$

$x + 2 \geq 5$ $\Rightarrow$ $x \geq 5 - 2$ $\Rightarrow$ $x \geq 3$

$x - 5 \leq 7$ $\Rightarrow$ $x \leq 7 + 5$ $\Rightarrow$ $x \leq 12$

$- 2 x > 5$ $\Rightarrow$ $x < - \frac{5}{2}$

$3 x \leq - 4$ $\Rightarrow$ $x \leq - \frac{4}{3}$

$- 3 x \geq - 12$ $\Rightarrow$ $- 3 x \geq \frac{- 12}{- 3}$ $\Rightarrow$ $x \geq 4$

$28 \leq - 7 x$ $\Rightarrow$ $\frac{28}{- 7} \geq \frac{- 7 x}{- 7}$ $\Rightarrow$ $x \leq - 4$

$42 < 6 x$ $\Rightarrow$ $x > 7$

$- 5 x \geq - 35$ $\Rightarrow$ $x \leq 7$

$2)$ Résoudre les inéquations suivantes :

$3 x + 5 > - 2$ $\Rightarrow$ $3 x > - 2 - 5$ $\Rightarrow$ $3 x > - 7$ $\Rightarrow$ $x > \frac{- 7}{3}$

$7 x + 5 < - 3$ $\Rightarrow$ $7 x < - 3 - 5$ $\Rightarrow$ $x < \frac{- 8}{7}$

$4 - 3 x \geq 2$ $\Rightarrow$ $- 3 x \geq 2 - 4$ $\Rightarrow$ $x \leq \frac{2}{3}$

$8 x + 3 \leq 6$ $\Rightarrow$ $8 x \leq 6 - 3$ $\Rightarrow$ $x \leq \frac{3}{8}$

$- 3 > - 5 x + 7$ $\Rightarrow$ $- 3 - 7 > - 5 x$ $\Rightarrow$ $x > 2$

$8 - 7 x \leq 4$ $\Rightarrow$ $- 7 x \leq 4 - 8$ $\Rightarrow$ $x \geq \frac{4}{7}$

$7 x + 2 > x + 6$ $\Rightarrow$ $7 x - x > 6 - 2$ $\Rightarrow$ $6 x > 4$ $\Rightarrow$ $x > \frac{2}{3}$

$- 4 x + 7 \leq 5 - x$ $\Rightarrow$ $- 4 x + x \leq 5 - 7$ $\Rightarrow$ $- 3 x \leq - 2$ $\Rightarrow$ $x \geq \frac{2}{3}$

Exercice 8:

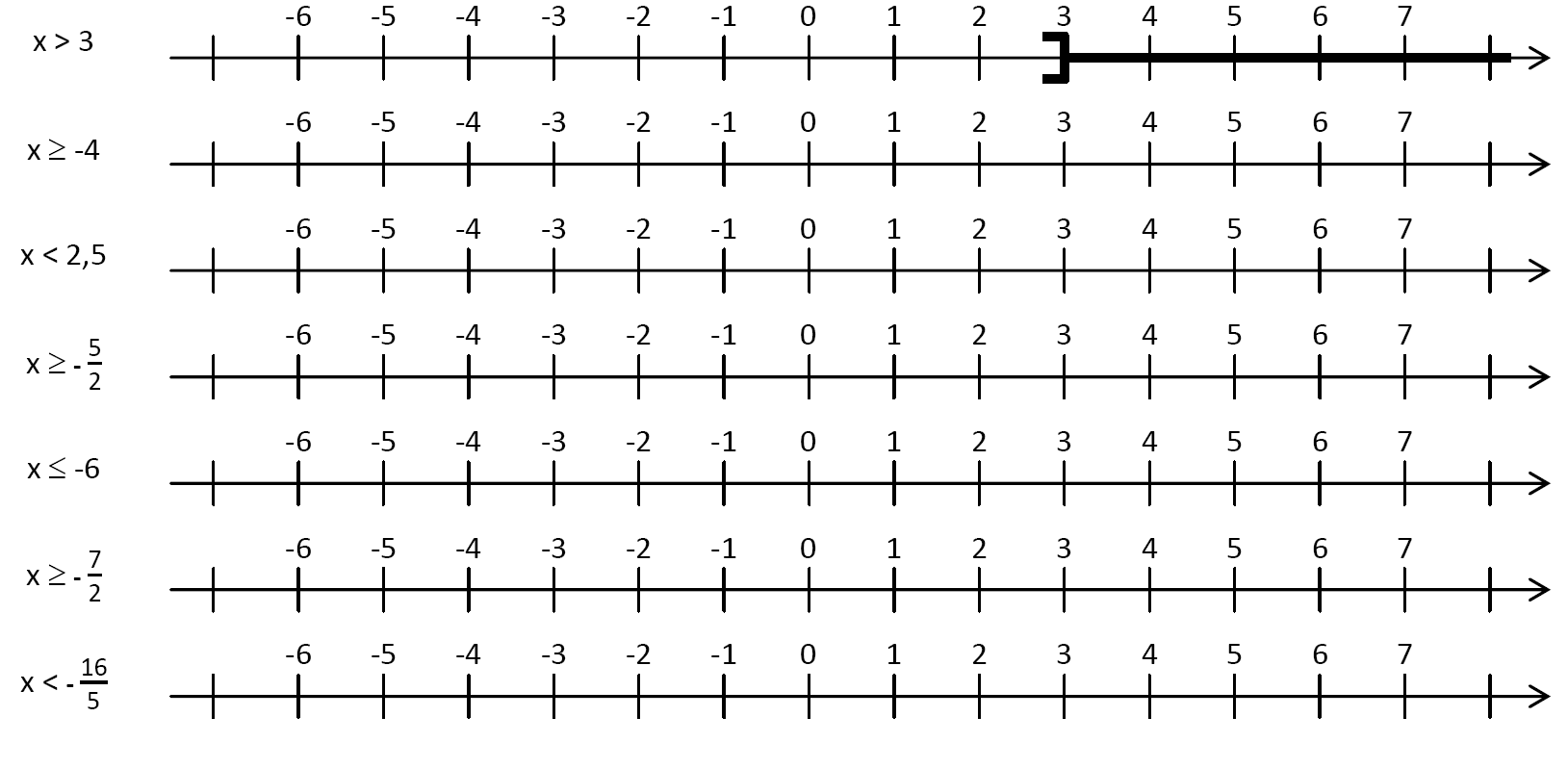
Repasser en couleur la partie de l’axe décrite par chaque inéquation :

Correction de l’exercice 8

Exercice 9:

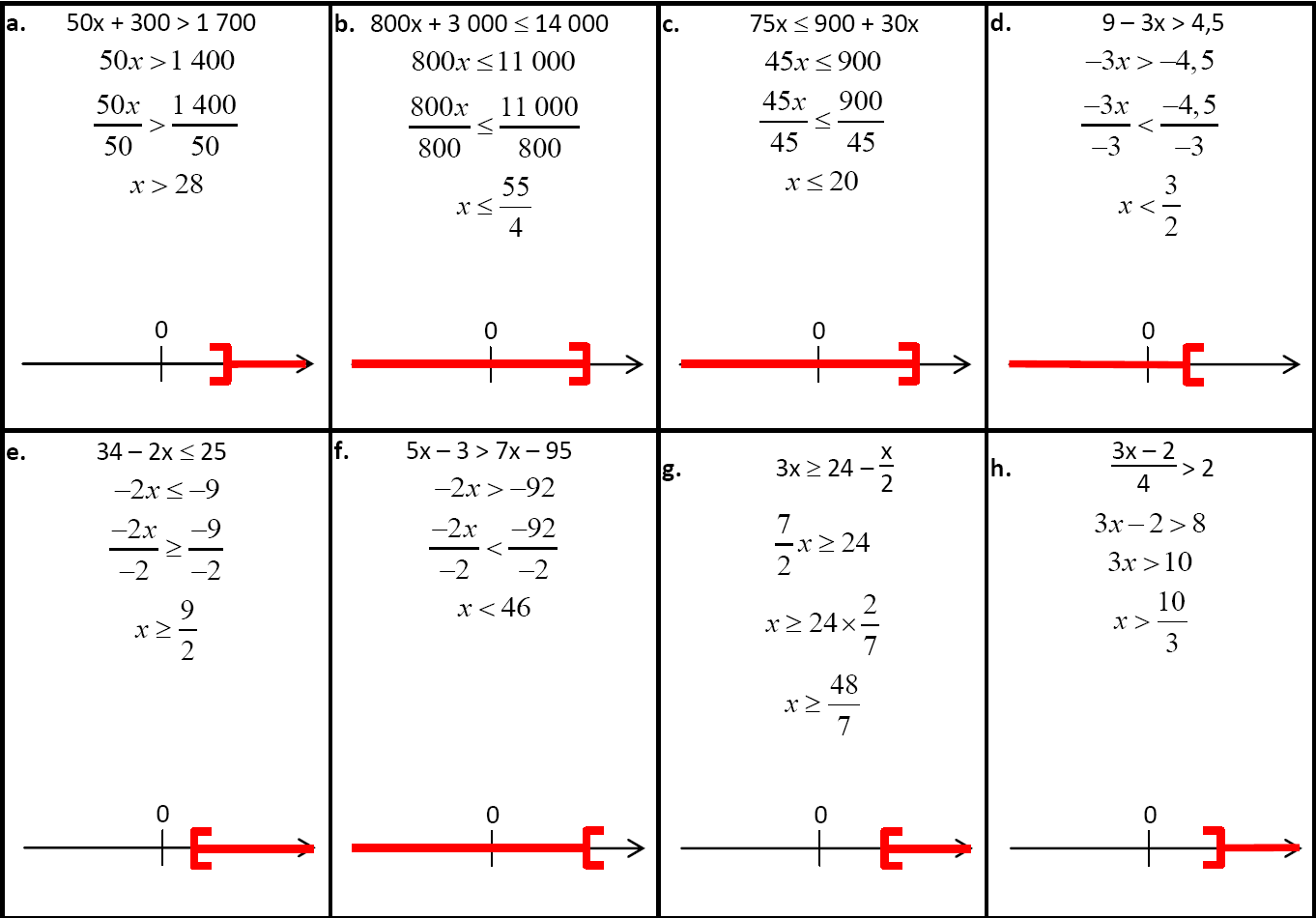
Résoudre chaque inéquation puis hachurer sur l’axe gradué la partie qui ne convient pas.

Correction de l’exercice 9

Exercice 10:

Résoudre les inéquations suivantes et représenter leur ensemble de solutions sur une droite graduée :

$a)$ $3 (2 x - 1) > 3 x + 2$

$b)$ $3 x - 8 \leq 8 (x - 2)$

$c)$ $- 2 (3 x + 1) \geq - x - 3$

$d)$ $\frac{2 x + 1}{3} - \frac{x - 1}{2} \leq 1$

$e)$ $\frac{3 + 2 x}{6} - \frac{3 + x}{8} < 0$

Correction de l’exercice 10

$a)$ $3 (2 x - 1) > 3 x + 2 \Rightarrow 6 x - 3 > 3 x + 2 \Rightarrow 6 x - 3 x > 2 + 3 \Rightarrow 3 x > 5 \Rightarrow x > \frac{5}{3}$

$b)$ $3 x - 8 \leq 8 (x - 2)$

$3 x - 8 \leq 8 x - 16$

$3 x - 8 x \leq 8 - 16$

$- 5 x \leq - 8$

$x \geq \frac{8}{5}$

$c)$ $- 2 (3 x + 1) \geq - x - 3 \Rightarrow - 6 x - 2 \geq - x - 3 \Rightarrow - 6 x + x \geq - 3 + 2 \Rightarrow - 5 x \geq - 1 \Rightarrow x \leq \frac{1}{5}$

$d)$ $\frac{2 x + 1}{3} - \frac{x - 1}{2} \leq 1 \Rightarrow \frac{2 (2 x + 1)}{6} - \frac{3 (x - 1)}{6} \leq \frac{6}{6} \Rightarrow 2 (2 x + 1) - 3 (x - 1) \leq 6 \Rightarrow 4 x + 2 - 3 x + 3 \leq 6 \Rightarrow 4 x - 3 x \leq 6 - 2 - 3 \Rightarrow x \leq 1$

$e)$ $\frac{3 + 2 x}{6} - \frac{3 + x}{8} < 0$

$\frac{4 (3 + 2 x)}{24} - \frac{3 (3 + x)}{24} < 0$

$4 (3 + 2 x) - 3 (3 + x) < 0$

$12 + 8 x - 9 - 3 x < 0$

$5 x < - 3$

$donc x < \frac{- 3}{5}$

Exercice 11:

$1)$ On considère l’inéquation : $4 x + 7 > 2 - 3 x$ .

$a)$ Le nombre $0$ est-il solution de cette inéquation ? Justifier la réponse.

$b)$ Le nombre $(- 1)$ est-il solution de cette inéquation ?Justifier la réponse.

$c)$ Résoudre l’inéquation $4 x + 7 > 2 - 3 x$ et représenter ses solutions sur une droite graduée.

$2)$ $a)$ Parmi les nombres : $0; (- 4); (- 5)$ retrouver ceux qui sont solutions de l’inéquation $1 - 5 x \leq 21$ .

$b)$ Résoudre l’inéquation $3 x - 2 \geq x - 4$ . Représenter graphiquement sur une droite graduée, les solutions de cette inéquation (hachurer la partie qui ne convient pas).

Correction de l’exercice 11

$1)$ $a)$ Le nombre $0$ est-il solution de cette inéquation?

$4 x + 7 = 4 \times 0 + 7 = 7$

$2 - 3 x = 2 - 3 \times 0 = 2$

$7 > 2$ donc 0 est solution de cette inéquation.

$b)$ Le nombre (-1) est-il solution de cette inéquation?

$4 x + 7 = 4 \times (- 1) + 7 = 3$

$2 - 3 x = 2 - 3 \times (- 1) = 5$

$3 < 5$ donc $- 1$ n’est pas solution de cette inéquation.

$c)$ $4 x + 7 > 2 - 3 x$

$7 x > - 5$

$x > \frac{- 5}{7}$

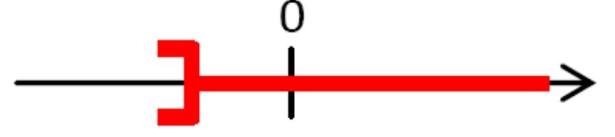
$2)$ $a)$ Parmi les nombres: $0; (- 4); (- 5)$ retrouver ceux qui sont solutions de l’inéquation $1 - 5 x \leq 21$ :

$1 - 5 \times 0 = 1 \to 1 \leq 21$

$1 - 5 \times (- 4) = 21 \to 21 \leq 21$

$1 - 5 \times (- 5) = 26 \to 26 > 21$

$0$ et $- 4$ sont les solutions de cette inéquation.

$a)$ $3 x - 2 \geq x - 4$

$2 x \geq - 2$

$x \geq - 1$

Exercice 12:

Dans une classe de $30$ élèves, la moyenne des filles est $13$ ; celle des garçons, $10, 5$ .
La moyenne de la classe est $11, 5$ .

Combien y a-t-il de garçons ?

Correction de l’exercice 12

Coup de pouce : Soit x le nombre de garçons, le nombre de filles est donc …..

Le nombre de filles est $30 - x$ , on a :

La somme des notes des filles est alors $13 \times (30 - x)$

La somme des notes des garçons est alors $10, 5 x$

La somme de toutes les notes est $30 \times 11, 5$

On a donc : $10, 5 x + 13 (30 - x) = 30 \times 11, 5$

$10, 5 x + 390 - 13 x = 345$

$10, 5 x - 13 x = 345 - 390$

$- 2, 5 x = - 45$

$x = \frac{45}{2, 5} = 18$

Le nombre de garçons est $18$ .

Exercice 13:

La moyenne d’une classe à un contrôle est $10, 2$ . L’un des élèves n’a rien su faire et a obtenu $0$ .

Le professeur décide de recalculer la moyenne sans compter cet élève.

La nouvelle moyenne est $10, 8$ .

Combien y a-t-il d’élèves dans cette classe ?

Correction de l’exercice 13

Soit n le nombre d’élèves.

Soit S la somme de toutes les notes.

On a $10, 2 = \frac{S}{n}$ et $10, 8 = \frac{S}{n - 1}$

Soit $S = 10, 2 \times n$ et $S = 10, 8 \times (n - 1)$

Donc $10, 2 \times n = 10, 8 \times (n - 1)$

Equation du premier degré dont l’inconnue est n.

$10, 2 \times n = 10, 8 \times (n - 1)$

$10, 2 n = 10, 8 n - 10, 8$

$10, 8 n - 10, 2 n = 10, 8$

$n = \frac{10, 8}{0, 6} = 18.$

Il y a $18$ élèves dans la classe.

Exercice 14:

Amal possède des pièces de $20 D H$ et des billets de $100 D H$ dans son porte-monnaie.

Elle a $560 D H$ en tout, et a deux fois plus de pièces que de billets.

Combien a-t-elle de billets dans son porte-monnaie ?

En déduire le nombre de pièces.

Correction de l’exercice 14

Soit $x$ le nombre de billets de 100 DH

Le nombre de pièces de $20 D H$ est égal à $2 x$ .

Les $x$ billets de $100 D H$ représentent la somme de $100 x D H$ .

Les $2 x$ pièces de $20 D H$ représentent la somme de $2 x \times 20 = 40 x D H$

La somme totale est égale à $560 D H$ .

On obtient donc l’équation : $100 x + 40 x = 560$

$140 x = 560$

$x = \frac{560}{140} = 4$

$S = 4$

Amal possède $4$ billets de $100 D H$ et $8$ pièces de $20 D H$ .

Exercice 15:

Je pense à un nombre.

Si je lui enlève $3$ , j’obtiens la moitié du nombre initial augmentée de $1$ .

A quel nombre ai-je pensé ?

Correction de l’exercice 15

Soit $x$ le nombre auquel j’ai pensé.

Si on lui enlève $3$ , on obtient le nombre $x - 3$

La moitié du nombre $x$ augmentée de $1$ est égale à : $\frac{x}{2} + 1$

On obtient donc l’équation : $x - 3 = \frac{x}{2} + 1$

$x - \frac{x}{2} = 1 + 3$

$\frac{2 x}{2} - \frac{x}{2} = 4$

$\frac{x}{2} = 4$

$x = 2 \times 4 = 8$

J’ai pensé au nombre $8$ .

Exercice 16:

Samir a acheté deux C.D. coûtant le même prix et il lui reste $95 D H$ .
Si chaque C.D. avait coûté $10 D H$ de moins, il aurait pu en acheter un de plus en dépensant toutes ses économies.

Quel est le prix d’un C.D. ?

Correction de l’exercice 16

Soit $x$ le prix d’un C.D.

Deux C.D. coûtent $2 x D H$ .

Arnaud possède la somme de $2 x + 95 D H$

Si un C.D. coûtait $10 D H$ de moins, il coûterait $x - 10 D H$ .

Samir pourrait s’acheter $3$ C.D. qui représentent la somme de $3 (x - 1) D H$ .

On obtient donc l’équation : $2 x + 95 = 3 (x - 10)$

$2 x + 95 = 3 x - 30$

$2 x - 3 x = - 30 - 95$

$- x = - 125$

$x = 125$

$S = 125$

Le prix d’un C.D. est de $125 D H$ .

Exercice 17:

La somme de trois entiers consécutifs est comprise entre $12$ et $27$ .

Quelles sont les valeurs possibles du plus grand de ces trois nombres ?

Correction de l’exercice 17

Soit $x$ le plus grand des trois entiers consécutifs.

Le précédent est égal à $x - 1$ et le plus petit est égal à $x - 2$ .

La somme de ces trois entiers est égale à : $(x - 2) + (x - 1) + x = 3 x - 3$

$12 < 3 x - 3 < 27$

$12 + 3 < 3 x - 3 + 3 < 27 + 3$

$15 < 3 x < 30$

$\frac{15}{3} < \frac{3 x}{3} < \frac{30}{3}$

$5 < x < 10$

Le plus grand de ces trois entiers est $6, 7, 8$ ou $9$ .

Exercice 18:

Le périmètre d’un rectangle est inférieur ou égal à $37 c m$ .

Sachant que sa largeur est égale à $5, 3 c m$ , déterminer les valeurs possibles pour la longueur de ce rectangle.

(La longueur doit être supérieure à la largeur)

Correction de l’exercice 18

Soit $L$ la longueur de ce rectangle.

$L > 5, 3 c m$

Le périmètre de ce rectangle est égal à : $2 L + 2 \times 5, 3 = 2 L + 10, 6$

$12 < 3 x - 3 < 27$

$12 + 3 < 3 x - 3 + 3 < 27 + 3$

$15 < 3 x < 30$

$\frac{15}{3} < \frac{3 x}{3} < \frac{30}{3}$

$5 < x < 10$

Conclusion : la longueur de ce rectangle est comprise entre $5, 3 c m$ et $13, 2 c m$ .

Exercice 19:

Une salle rectangulaire, représentée par le rectangle $A B C D$ sur le dessin, peut être partagée en deux parties rectangulaires au moyen d’une cloison mobile, représentée par le segment $[M N]$ .

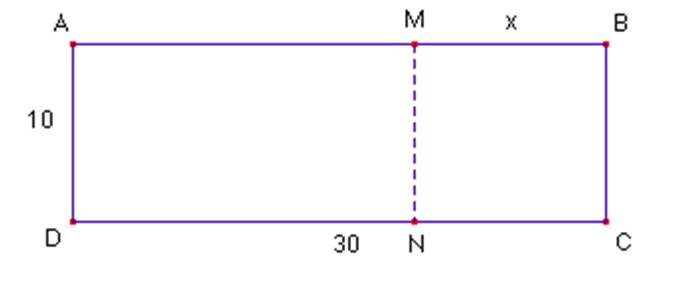
Les dimensions, exprimées en mètres, sont portées sur le dessin : $A D = 10$ ; $D C = 30$ ; $M B = x$ .

La valeur de $x$ permet de repérer la position de la cloison mobile.

$1)$ Que représente l’expression $10 (30 - x)$ exprimée en $m^{2}$?

$2)$ Que représente l’expression $10 x$ exprimée en $m^{2}$?

$3)$ Résoudre l’inéquation $300 - 10 x < 40 x$

$4)$ Trouver les valeurs de $x$ pour lesquelles l’aire de la partie $A M N D$ est inférieure à quatre fois l’aire de la partie $M B C N$

Correction de l’exercice 19

$1)$ Que représente l’expression $10 (30 - x)$ exprimée en $m^{2}$

l’aire de la partie $A M N D$

$2)$ Que représente l’expression $10 x$ exprimée en $m^{2}$

l’aire de la partie $M B C N$

$3)$ Résoudre l’inéquation $300 - 10 x < 40 x$

$300 < 40 x + 10 x$

$300 < 50 x$

$x > \frac{300}{50}$

$x > 6$

$4)$ Trouver les valeurs de x pour lesquelles l’aire de la partie $A M N D$ est inférieure à quatre fois l’aire de la partie $M B C N$ .

Il faut que $x > 6$

Exercice 20:

Sonia a eu $11$ notes dont la moyenne est $13, 7$ sur $20$ .

Quelles notes à son prochain devoir lui permettront d’obtenir une moyenne supérieure ou égale à $14$ ?

Correction de l’exercice 20

Si elle a eu $11$ notes et sa moyenne est de $\frac{13.7}{20}$ cela signifie qu’elle a eu $11$ fois $13.7$

Soit x la future note de Sonia :

donc on peut l’écrire $\frac{(11 \times 13.7 + x)}{12}$ (pour faire une moyenne) $14$

$\frac{(11 \times 13.7 + x)}{12} \geq 14$

$\frac{(150.7 + x)}{12} \geq 14$

$150.7 + x \geq 12 \times 14$

$150.7 + x \geq 168$

$150.7 + x \geq 168 - 150.7$

$x \geq 17.3$

Il faut qu’elle ait au minimum $17.3$ pour que sa moyenne soit supérieure ou égale à $14$

Équations et inéquations exercices corrigés