Examens locaux corrigés mathématiques 3AC
Examen normalisé No 1
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
6,50 points
1- Calculer et simplifier les expressions suivantes :
\[A = 2\sqrt{20} – \sqrt{45} + \sqrt{125}\]
\[B = \frac{1}{25} – \left( \frac{2}{3} \right)^{-2}\]
\[C = \sqrt{2\sqrt{7} + \sqrt{3}} \times \sqrt{2\sqrt{7} – \sqrt{3}}\]
2- Déterminer l’écriture scientifique de E et F :
\[E = 0,004 \times 10^{-6} \times 12 \times (10^2)^{-4}\]
\[F = 0,005 \times 20000 \times (0,0002)^3\]
3- Développer G puis Factoriser H tels que :
\[G = (2 + \sqrt{5})^2 – (1 – \sqrt{5})^2\]
\[H = (x – 2)^2 – x^2 + 4\]
4- Comparer : \(-2\sqrt{7}\) et \(-\sqrt{5}\).
5- Soit a un nombre réel positif. Montrer que : \((a + 1)^2 \geq 1 + 2a\).
6- Soient \(x\) et \(y\) deux nombres réels tels que :
| \(1 \leq x \leq 3\) | \(-6 \leq y \leq -2\) |
|---|
Encadrer chacun des nombres :
| \(2x – y\) | \(xy + 1\) |
|---|---|
| \(x^2 + y^2 – 1\) | \(-3y + x^2\) |
7- Montrer que : \(0 \leq \frac{x^2 + y^2 – 5}{20} \leq 2\)
Exercice Numéro 2
2,50 points
Soit α la mesure d’un angle aigu tel que :
\[\cos α = \frac{2\sqrt{2}}{3}\]
1- Calculer les rapports : \(\sin α\) et \(\tan α\)
2- Montrer que :
\[(\sin α)(\cos α) \left( \frac{1}{\tan α} \right) + \sin^2 α = 1\]
3- Calculer l’expression suivante :
\[G = \cos 14^\circ + \sin 28^\circ + \sin 26^\circ – \sin 76^\circ – 2 \tan 35^\circ \times \tan 55^\circ\]
4- Soit ABC le triangle défini ainsi : AC = 6 cm, AB = 3 cm, BC = 3\(\sqrt{5}\) cm.
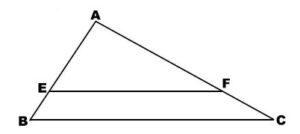
a. Montrer que le triangle ABC est rectangle en A.
b. Calculer les rapports : \(\cos \widehat{AB}\) et \(\tan \widehat{AB}\).
5- Soit E un point de [AB] tel que AE = 2,5 cm. La droite parallèle à (BC) passant par E coupe (AC) en F. Calculer la distance AF.
Exercice Numéro 3
3,50 points
Sur la figure ci-dessous : EJM et AMB sont deux triangles rectangles respectivement en E et B tels que : EM = 1,5 cm, BM = 3 cm, EJ = 2 cm, MJ = 2,5 cm, JN = 8 cm, P est le symétrique de M par rapport à B.
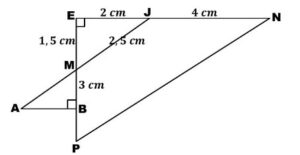
1. Calculer les distances AM et AB.
2. Montrer que : (MJ) // (NP). En déduire PN.
Exercice Numéro 4
2,50 points
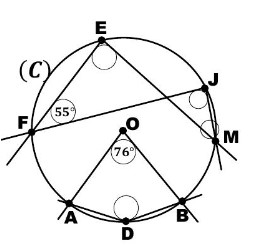
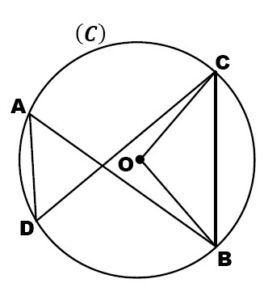
On considère la figure ci-jointe où (C) est un cercle de centre O et les points A, B, D, E, F, J et M appartiennent au cercle (C). Et
\[\widehat{AOB} = 76^\circ\]
\[\widehat{EFG} = 55^\circ\]
1. Calculer la mesure de l’angle \(\widehat{EMJ}\) en justifiant la réponse.
2. Montrer que : \(\widehat{ADB} = 142^\circ\).
Exercice Numéro 5
5,00 points
Soit ABCD un parallélogramme. Soit J le milieu du segment [CD]. La droite (AJ) coupe la droite (BC) en un point K.
1. Montrer que ADJ et KCJ sont isométriques.
2. Montrer que ADJ et KBA sont semblables.
🔒 Abonnez-vous pour accéder à la correction détaillée .
Examen normalisé No 2
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
05,50 points
1- Calculer puis simplifier les expressions :
\[A = 2\sqrt{9} – 3\sqrt{25} + \sqrt{36}\]
\[B = \frac{\sqrt{300}}{\sqrt{3}}\]
\[C = \left( \frac{1}{\sqrt{2}} \right)^{-2}\]
\[C = \sqrt{18} + \sqrt{8} – 5\sqrt{2}\]
2- Développer puis simplifier les expressions :
\[D = \left( 2 + \sqrt{5} \right)^2 – 4\sqrt{5}\]
\[E = \left( 1 + \sqrt{2} \right)^3 – 5\sqrt{2}\]
3- Rendre le dénominateur un entier naturel :
\[X = \frac{3}{\sqrt{3}}\]
\[Y = \frac{2}{\sqrt{3} – 1}\]
4- En déduire que : \(Y – X = 1\).
5- Déterminer l’écriture scientifique de :
\[M = (0,004)^2 \times (50000)^2\]
\[N = (0,00003)^3 \times 10000\]
Exercice Numéro 2
03,50 points
1- Comparer les nombres 4 et \(3\sqrt{2} \).
2- En déduire que : \(4 + 2\sqrt{2} \leq 5\sqrt{2}\).
3- Soient x et y deux nombres réels tels que :
| \(3 \leq x \leq 5\) | \(2 \leq y \leq 6\) |
|---|
Trouver un encadrement pour les expressions :
| \(2x + y\) | \(-2y + 5x\) | \(2x^2 – y^2\) | \(\frac{2x}{x+y}\) |
|---|
4- Soient a et b deux nombres réels tels que :
\[a \geq 0 \quad et \quad b \leq 2\]
Montrer que : \(ab \leq 2a\).
Exercice Numéro 3
04,00 points
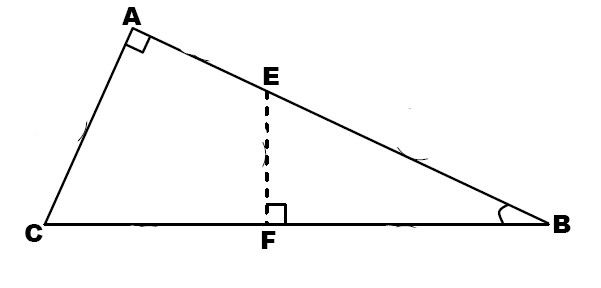
1- Soit ABC un triangle tel que : AB=4cm, BC=6cm, AC=\(2\sqrt{5}\)cm.
Montrer que le triangle ABC est rectangle en A.
2- Soit E un point de [AB] tel que BE = 3 cm, Soit F Le projeté orthogonal de E sur (BC).
Montrer que : EF=\(\sqrt{5}\)cm.
En déduire la distance FB.
3- Soit x la mesure d’un angle aigu tel que :
\[\cos x = \frac{\sqrt{2}}{3}\]
Montrer que : \(\sin x = \frac{\sqrt{7}}{3}\). En déduire : \(\tan x\).
4- Soit a la mesure d’un angle aigu non nul.
Montrer que : \((\sin a – \cos a)^2 – 1 = -2\sin a\cdot \cos a\)
Exercice Numéro 4
03,50 points
Sur la figure ci-jointe, on a (MN)//(BC).
Et on a : AM=3cm, AB=9cm, AC=7,5cm
1- Calculer la distance AN.
2- Soit E un point de la demi-droite [AC] tel que : AE = 3AC. Calculer les rapports :
\[\frac{AC}{AE} \quad et \quad \frac{AM}{AB}\]
3- En déduire que : (EB)//(MC).
Exercice Numéro 5
03,50 points
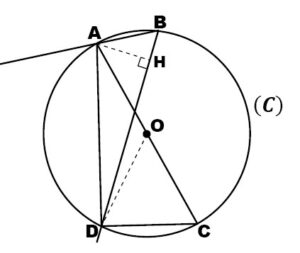
Soient A, B, C, D quatre points du cercle (C) de centre O tel que [AC] est l’un de ces diamètres.
Soit H le projeté orthogonal du point A sur (BD) et \(\widehat{ABD}=48^\circ\).
1- Calculer les mesures des angles : \(\widehat{AOD}\) et \(\widehat{ACD}\).
2- Montrer que : \(\widehat{ADC}=90^\circ\).
3- Montrer que les triangles AHB et ADC sont semblables.
4- En déduire que : \(AC \times AH = AD \times AB\).
🔒 Abonnez-vous pour accéder à la correction détaillée .
Examen normalisé No 3
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
06,00 points
1- Calculer puis simplifier les expressions :
\[A = \sqrt{16 + 96 – 1} \]
\[B = \sqrt{3 + \sqrt{300} – \sqrt{12}} \]
\[C = \frac{\sqrt{2}}{2\sqrt{2}} + \frac{\sqrt{8}}{\sqrt{2}} + 1 \]
\[D = \frac{2}{2 + \sqrt{3}} + \frac{\sqrt{3}}{2 – \sqrt{3}} \]
2- Donner l’écriture scientifique des expressions :
\[E = (500000)^2 \times 100 \]
\[F = (0,000002 \times 5000)^5 \]
Exercice Numéro 2
04,50 points
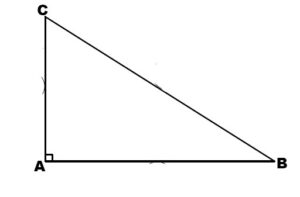
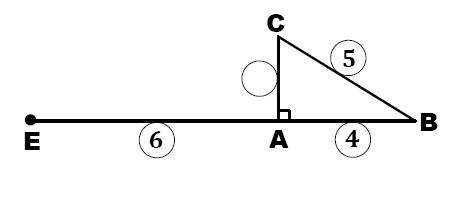
Soit ABC un triangle rectangle tel que : AC=3cm, AB=4cm.
1. Calculer la distance BC.
2. Calculer les rapports : \( \sin A \hat{B} C \) et \( \tan A \hat{B} C \).
3. Soit E le symétrique de C par rapport à A.
et H le projeté orthogonal de E sur (BC).
Recopier puis compléter la figure ci-dessus.
4. Montrer que : CH = 3,6cm .
Calculer l’expression suivante :
\[P = \sin^2 10^\circ + 2 \sin^2 45^\circ + \sin^2 80^\circ \]
Exercice Numéro 3
03,00 points
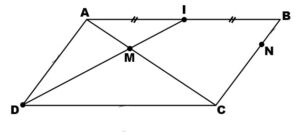
Sur la figure ci-dessous : ABCD est un parallélogramme tel que AB=10 cm, AD=6 cm et I est le milieu de [AB] et BN=2.
1. Montrer que : \(\frac{MA}{MC} = \frac{1}{2}\)
2. Montrer que : (MN)//(AB).
Exercice Numéro 4
01,50 points
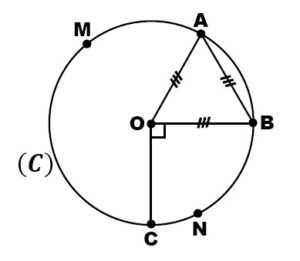
Sur la figure ci-dessous, OAB est un triangle équilatéral et \( B \hat{O} C = 90^\circ \).
1. Calculer la mesure de l’angle \( A \hat{M} B \).
2. Calculer la mesure de l’angle \( C \hat{N} B \).
Exercice Numéro 5
02,50 points
Soit ABCD un rectangle tel que : AB=6cm et AD=4cm. E est un point du segment [AB] tel que BE=2cm et F est le milieu du segment [AD]
1. Faire une construction géométrique.
2. Montrer que les triangles EBC et AEF sont isométriques.
3. Montrer que le triangle EFC est isocèle en E.
4. Montrer que le triangle EFC est rectangle en E.
Exercice Numéro 6
02,50 points
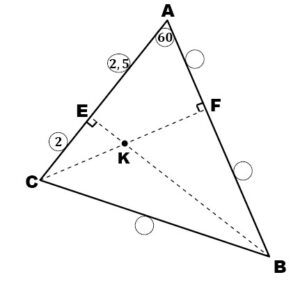
Soit ABC un triangle. E est le projeté orthogonal du point B sur (AC) et F est le projeté orthogonale du point C sur (AB). On pose :
AE=2,5cm, AC=4,5cm, \( B \hat{A} C = 60^\circ \), \( \sin 30^\circ = 1/2 \)
1. Montrer que AFC et AEB sont semblables.
2. Calculer les distances AF et AB.
3. Montrer que ABC et AFE sont semblables.
🔒 Abonnez-vous pour accéder à la correction détaillée .
Examen normalisé No 4
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
05,50 points
Calculer puis simplifier les expressions :
\[A = \sqrt{2} \times \sqrt{10} \times \sqrt{5} – 9\]
\[B = \sqrt{45} – \sqrt{5} + 3\sqrt{20}\]
\[C = \frac{\sqrt{7} + 3}{\sqrt{7} – 1}\]
\[D = \left( \frac{1}{5\sqrt{2}} \right)^{-2}\]
Donner l’écriture scientifique des nombres :
\[E = (0,000000002)^5\]
\[F = \left( 0,002 \times 500^2 \times 4000 \right)^6\]
\[G = \left( \frac{240000 \times 300}{0,0000036} \right)^4\]
Développer puis réduire les expressions :
\[H = \left( 1 – 2\sqrt{3} \right)^2 + 4\sqrt{3} + 1\]
\[I = \left( \sqrt{8} – \sqrt{2} \right)^2 – 1\]
Factoriser les expressions suivantes :
\[J = \left( 1 + \sqrt{3} \right)^2 – 1\]
\[K = \left( x^2 – 3 \right) + 2x\left( x – \sqrt{3} \right)\]
Exercice Numéro 2
04,50 points
Soit ABC un triangle rectangle en A tel que : AB=4cm et BC=5cm.
1. Montrer que AC=3cm.
2. Calculer les rapports : sin \( ABC \) et cos \( ABC \).
3. Soit E un point de \([BA]\) tel que AE=6cm.
4. Soit K le projeté orthogonal de E sur \([BC]\).
Recopier puis compléter la figure ci-dessous :
5. Calculer la distance EK.
6. Soit a le mesure d’un angle aigu non nul tel que : sin \( a = \frac{\sqrt{5}}{3} \). Calculer : cosa.
Exercice Numéro 3
04,00 points
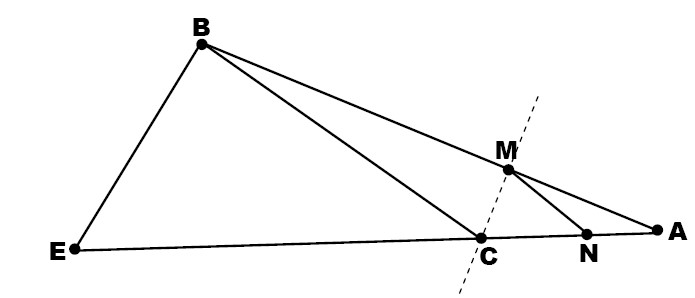
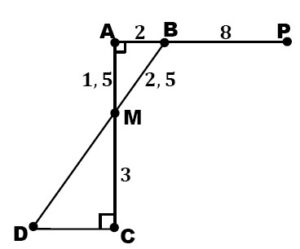
Sur la figure ci-dessous, ABM et DCM sont deux triangles rectangles respectivement en A et C tel que :
BP=8cm, MC=3cm, BM=2,5cm, AM=1,5cm, AB=2cm.
1. Soit N le symétrique de M par rapport à C. Recopier puis compléter la figure ci-dessous.
2. Calculer les distances DC et DM.
3. Montrer que : \([MB] / [NP]\).
Exercice Numéro 4
03,00 points
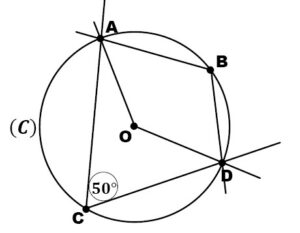
Soient A, B, C, et D quatre points d’un cercle (C) de centre O tel que : \( A\widehat{C}D = 50^\circ\).
1. Calculer la mesure de l’angle \( A\widehat{O}D \).
2. Montrer que : \( A\check{O}D = 260^\circ \).
3. En déduire la mesure de l’angle \( A\widehat{B}D \).
Exercice Numéro 5
03,00 points
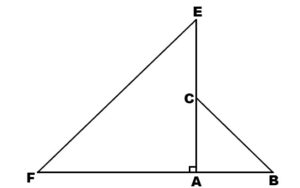
Sur la figure ci-dessous, ABC et AEF sont deux triangles rectangles et isocèles en A.
1. Montrer que les triangles ABE et ACF sont isométriques.
2. La droite (BC) coupe (EF) en H. Montrer que les triangles ABC et FBI sont semblables.
Examen normalisé No 5
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
04,50 points
Calculer puis simplifier les expressions suivantes :
\[A = \sqrt{6} \times \sqrt{42} \times \sqrt{21} – 2\sqrt{3}\]
\[B = \sqrt{54} + \sqrt{600} – 5\sqrt{24}\]
\[C = \frac{1}{\sqrt{12} + \sqrt{3}} + \frac{1}{\sqrt{3}}\]
Donner l’écriture scientifique des expressions :
\[D = (5000)^2 \times (0,0002)^2 \times (100)^{-6}\]
\[E = 125000 \times (0,000002)^3 \times 0,001\]
Développer puis réduire les expressions :
\[F = \left(2 + \sqrt{3}\right)^2 – \left(1 – \sqrt{3}\right)^2\]
\[G = \left(2\sqrt{8} + 1\right)\left(3\sqrt{2} – 1\right)\]
Factoriser l’expression suivante :
\[H = \left(1 + \sqrt{2}\right)^2 – \left(1 – \sqrt{2}\right)^2\]
\[I = 4x^2 + 4x + 1\]
Exercice Numéro 2
04,00 points
Comparer les nombres : \(2\sqrt{7}\) et \(7\sqrt{2}\).
Soient a et b deux nombres réels tels que :
\(1 \leq a \leq 2\) et \(-3 \leq b \leq -2\)
Encadrer les expressions suivantes :
\(2a + 3b\), \(a – 2b\), \(3ab\)
Montrer que :
\(0 \leq \frac{2\sqrt{b^2 – a^2}}{\sqrt{2 – ab}} \leq 2\sqrt{2}\)
Exercice Numéro 3
03,50 points
Sur la figure ci-dessous, On a : \((EF) // (BC)\). Et : AE=2cm, AB=5cm, BC=6cm.
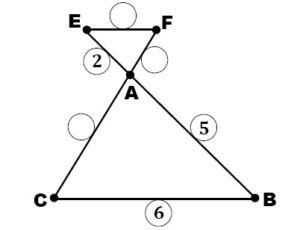
1. Calculer la distance EF.
2. M est un point de \([AB]\) et N un point de \([BC]\) tels que : BM=1cm et BN=1,2cm
• Montrer que : \((MN) // (AC)\).
3. Montrer que : AC=5MN.
Exercice Numéro 4
04,00 points
Soit ABC un triangle défini par ces côtés : AB=2cm, \(AC = 2\sqrt{3} \)cm, BC=4cm.
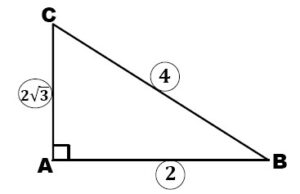
1. Montrer que le triangle ABC est un triangle rectangle en A.
2. Calculer : \(\sin ABC\), \(\cos ABC\) et \(\tan ABC\).
3. En déduire la mesure de l’angle \(ABC\).
4. \(a\) est la mesure d’un angle aigu non nul tel que \(\cos a = \frac{\sqrt{15}}{4}\). Calculer \(\sin a\).
5. Calculer l’expression suivante :
\[(\cos 87^\circ)^2 + 4(\cos 60^\circ)^2 + \left(\frac{\sin 10^\circ}{\cos 10^\circ}\right)(\tan 80^\circ) + (\cos 3^\circ)^2\]
Exercice Numéro 5
04,00 points
Sur la figure ci-jointe, On a O est le centre du cercle \((C)\) et \(\widehat{ABC}=80^\circ\) et \(\widehat{BOC}=170^\circ\).
1. Calculer la mesure de l’angle \(\widehat{ADC}\).
2. Calculer la mesure de l’angle \(\widehat{BAC}\).
3. Calculer la mesure de l’angle \(\widehat{CDB}\).
Examen normalisé No 6
NIVEAU : 3ème Année secondaire collégiale
SESSION ORDINAIRE : Janvier
Exercice Numéro 1
06,00 points
Calculer les expressions suivantes :
\[A = \sqrt{\frac{1}{16} + \left( \frac{4}{3} \right)^{-1}}\]
\[B = \sqrt{8\sqrt{2} \times \sqrt{2} – 2\sqrt{3} + 1}\]
\[C = \sqrt{50 – 2\sqrt{18} + 4\sqrt{2}}\]
\[D = \sqrt{2\sqrt{5} + 2 \times \sqrt{2\sqrt{5} – 2}}\]
Donner l’écriture scientifique des nombres :
\[E = \sqrt{0,000004 \times (20000)^3 \times 1000}\]
\[F = (0,005)^3 \times (2000)^3 \times 3300\]
Développer puis simplifier les expressions :
\[G = (\sqrt{3} – 2)^2 – 3\sqrt{2}(\sqrt{8} + \sqrt{2})\]
\[H = (2x – 1)(3x + 1) + 1\]
Factoriser les expressions :
\[I = (\sqrt{5} – 2)^2 – 3\sqrt{5}(2 – \sqrt{5})\]
\[J = 2x(x – 3) + (x^2 – 9)\]
Exercice Numéro 2
04,00 points
Comparer les nombres : \(2\sqrt{6}\) et \(5\)
En déduire une comparaison des nombres :
\(\frac{1}{2(\sqrt{6} – 2)}\) et \(1\)
Soient \(a\) et \(b\) deux nombres réels tels que :
\(4 \leq a \leq 5\) et \(-3 \leq b \leq -2\)
Encadrer les expressions suivantes :
\(2a – 3b + 1\), \(2ab – 1\), \(-2a – b^2 + 1\)
Encadrer les expressions suivantes :
\(2a^2 – b + 1\), \((a – b)(a + b)\), \(a^2 + ab + 1\)
Soit \(c\) un nombre réel tel que : \(0 \leq \sqrt{2c – 2} \leq 2\)
Trouver un encadrement du nombre \(c\).
Exercice Numéro 3
02,00 points
\(x\) est la mesure d’un angle aigu et : \(\sin x = \frac{2\sqrt{2}}{3}\)
1. Calculer les rapports : \(cos x\) et \(tan x\).
2. Calculer les expressions suivantes :
\[M = sin^275^\circ + sin^215^\circ + cos^265^\circ + cos^225^\circ\]
\[N = sin^230^\circ + 2sin20^\circ – 2cos70^\circ + sin^260^\circ\]
3. Montrer que : \(1 + tan^2 y = \frac{1}{cos^2 y}\)
Exercice Numéro 4
02,50 points
Calculer les distances DE, DF, FH, GH, Sachant que : \((DG)/f(F)\) et \(G\hat{D}H = G\hat{F}D = H\hat{E}F = 90^\circ\).
Montrer que DGF et DFE et EFH sont semblables
Exercice Numéro 5
02,50 points
On considère la figure ci-dessous où (C) est un cercle de centre O et ABC est un triangle isocèle en A et \(B\hat{O}M = 130^\circ\).
Calculer, en justifiant la réponse, la mesure de l’angle \(ACN\).
Exercice Numéro 6
03,00 points
Soit ABC un triangle et E un point de [BC] et F un point de [AB] tels que : BC=9cm, AC=4,5cm, AB=10,5cm, BE=3cm, BF=3,5cm.
1. Établir une construction géométrique.
2. Montrer que ABC et FBE sont semblables.
3. Calculer la distance EF.
🔒 Abonnez-vous pour accéder à la correction détaillée .
Examens locaux corrigés mathématiques 3AC
