Fonction linéaire et fonction affine exercices corrigés
Exercice 1:
Soit la fonction linéaire $f(x)= 2x$.
$1)$ Quelle est l’image de $3$ ?
$2)$ Quel nombre a pour image $-8$ ?
$3)$ Compléter :
$f(20) = ….$
$f(….) = 20$
$1)$ $A(2 ; 0)$ et $B(4 ; 1)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{1-0}{4-2}=\frac{1}{2}$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=\frac{1}{2} x+b$.
Le point $A(2 ; 0)$ appartient à la droite $(A B)$. Ses coordonnées vérifient donc l’équation précédente
On obtient ainsi : $0=\frac{1}{2} \times 2+b$ soit $0=1+b$ et $b=-1$.
L’équation réduite de $(A B)$ est donc $y=\frac{1}{2} x-1$.
On vérifie avec les coordonnées de $B: \frac{1}{2} x_{B}-1=\frac{1}{2} \times 4-1=2-1=1=y_{B}(:)$
$2)$ $A(-2 ; 1)$ et $B(-3 ; 5)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{5-1}{-3-(-2)}=\frac{4}{-1}=-4$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=-4 x+b$.
Le point $A(-2 ; 1)$ appartient à la droite $(A B)$. Ses coordonnées vérifient donc l’équation précédente
On obtient ainsi : $1=-4 \times(-2)+b$ soit $1=8+b$ et $b=-7$.
L’équation réduite de $(A B)$ est donc $y=-4 x-7$.
On vérifie avec les coordonnées de $B:-4 x_{B}-7=-4 \times(-3)-7=12-7=5=y_{B} \%$
$3)$ $A\left(\frac{1}{2} ; \frac{2}{3}\right)$ et $B\left(\frac{7}{6} ;-\frac{1}{5}\right)$
Les points $A$ et $B$ n’ont pas la même abscisse. L’équation réduite de la droite ( $A B$ ) est donc de la forme $y=a x+b$.
$a=\frac{-\frac{1}{5}-\frac{2}{3}}{\frac{7}{6}-\frac{1}{2}}=\frac{-\frac{13}{15}}{\frac{2}{3}}=-\frac{13}{10}$.
Par conséquent l’équation réduite de $(A B)$ est de la forme $y=-\frac{13}{10} x+b$.
Le point $A\left(\frac{1}{2} ; \frac{2}{3}\right)$ appartient à la droite $(A B)$.
Ses coordonnées vérifient donc l’équation précédente.
On obtient ainsi : $\frac{2}{3}=-\frac{13}{10} \times \frac{1}{2}+b$ soit $\frac{2}{3}=-\frac{13}{20}+b$ et $b=\frac{79}{60}$.
L’ équation réduite de $(A B)$ est donc $y=-\frac{13}{10} x+\frac{79}{60}$.
On vérifie avec les coordonnées de $B:-\frac{13}{10} x_{B}+\frac{79}{60}=-\frac{13}{10} \times \frac{1}{2}+\frac{79}{60}=-\frac{13}{20}+\frac{79}{60}=\frac{40}{60}=\frac{1}{5}=y_{B}()$
$4)$ $A(-1 ; 5)$ et $B(-1 ; 2)$
$A$ et $B$ ont la même abscisse $-1$ .
Par conséquent l’équation réduite de $(A B)$ est $x=-1$.
Exercice 2:
Soit la fonction linéaire $g(x)= -3x$.
$1)$ Quelle est l’image de $-2$ ?
$2)$ Quel nombre a pour image $-15$ ?
$3)$ Compléter :
$g(5) = ….$
$g(….) = 18$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 3:
Soit la fonction linéaire $f(x)= ax$.
$1)$ Déterminer le coefficient de cette fonction pour que $f(2) = -4$.
$2)$ Déterminer le coefficient de cette fonction pour que $f(12) = -4$.
$3)$ Déterminer le coefficient de cette fonction pour que $f(2) = 7$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 4:
Rappel : Dans un repère, la représentation graphique de la fonction $f(x)= ax$ est La droite passant par l’origine du repère et par le point de coordonnées (1 ; a).
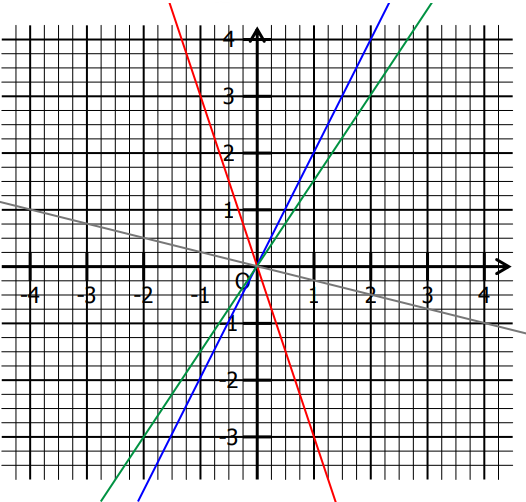
Représenter dans ce repère les fonctions linéaires suivantes :
– En bleu la fonction $f(x)= 2x$
– En rouge la fonction $g(x)= -3x$
– En vert la fonction $h(x)= \frac{3}{2}x$
– En gris la fonction $k(x)= -\frac{1}{4}x$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 5:
On a représenté dans un repère la fonction linéaire $f(x)= ax$
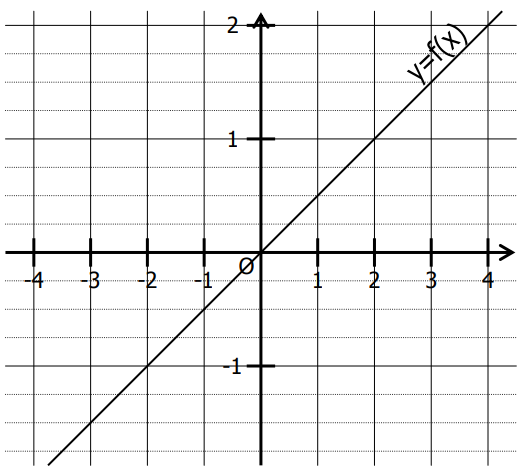
$1)$ Compléter en lisant sur le graphique :
$f(4) = ……$
$f(……) = 1$
$f(-2) = ……$
$2)$ Compléter : $f(1) = ……$
$3)$ En déduire la définition de $f(x)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 6:
On a représenté dans un repère les fonctions linéaires $f, g $et $h$ :
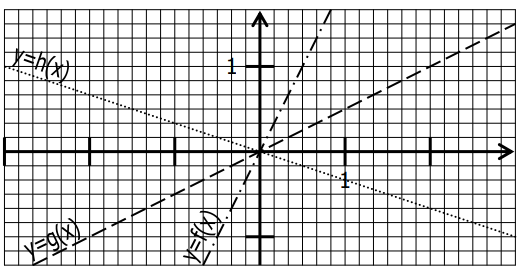
$1)$ Compléter en lisant sur le graphique :
$f(\frac{1}{6}) = ……$
$g(2) = …..$
$h(-2) = ….$
$f(…..) = -\frac{2}{3}$
$g(…..) = \frac{3}{2}$
$h(…..) = 1$
$2)$ Déterminer les coefficients des fonctions linéaires $f, g$ et $h$ :
$f (x)=….x$
$g(x)= ….x$
$h(x)=….x$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 7:
$1)$ Retrouver la fonction linéaire qui correspond à chaque phrase :
$a.$ « Prendre$ 5 %$ de $x$ » $f(x )= 0,05x$
$b.$ « Augmenter x de $5 %$ » $f(x)= …………$
$c.$ « Diminuer x de $5 %$ » $f(x)= …………$
$2)$ Retrouver la phrase (« Augmenter $x$ de … $%$ » ou « Diminuer vx$ de … $%$ ») qui correspond à chaque fonction linéaire :
$a.$ $f(x)= 0,97 x$ « …………….. x de …… $% $»
$b.$$ f(x)= 1,08 x $« …………….. x de ……$ %$ »
$c.$ $f(x)= 0,5 x $« …………….. x de …… $% $»
$3)$ Calculer (résultats arrondis à l’unité) :
$a.$ $267$ augmenté de $25 %$ :
$b.$ $267$ diminué de $41 %$ :
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 8:
$1)$ A l’occasion des soldes, un commerçant décide d’une baisse de $25 %$ sur tous les textiles.
$a.$ Définir la fonction linéaire qui permet de transformer le prix initial $ « x »$ en prix soldé
$b. $Recalculer le nouveau prix des étiquettes suivantes après la baisse de $25 %$
T-Shirt : $149 DH$
Polo : $199 DH$
Survêtement : $999 DH$
$2)$ Une paire de chaussure coûtait $890DH$ avant les soldes, et coûte désormais $690DH$.
$a.$ Calculer le coefficient de la fonction linéaire $g(x) = ………$ sachant que $g(890)= 690$
$b.$ En déduire le pourcentage de la réduction.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 9:
$f$ est une fonction affine de la forme : $f(x)= ax + b$
$1)$ Déterminer $a$ et $b$ sachant que : $f(2) = 5$ et $f(7) = 15$
$2)$ Déterminer $a$ et $b$ sachant que : $f(3) = 1$ et $f(5) = 9$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 10:
Rappel : Dans un repère, la représentation graphique de la fonction affine $g(x)= ax + b$ est la droite :
• parallèle à la droite représentant la fonction linéaire associée ;
• passant par le point de coordonnées $(0 ; b)$
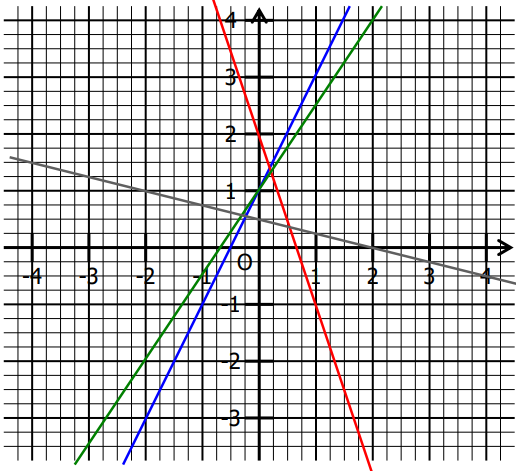
Représenter dans ce repère les fonctions linéaires suivantes :
– En bleu la fonction $f(x)= 2x+1$
– En rouge la fonction $g(x)= -3x+2$
– En vert la fonction $h(x)= \frac{3}{2}x+1$
– En gris la fonction $k(x)= -\frac{1}{4}x+\frac{1}{2}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 11:
On a représenté dans un repère la fonction affine.
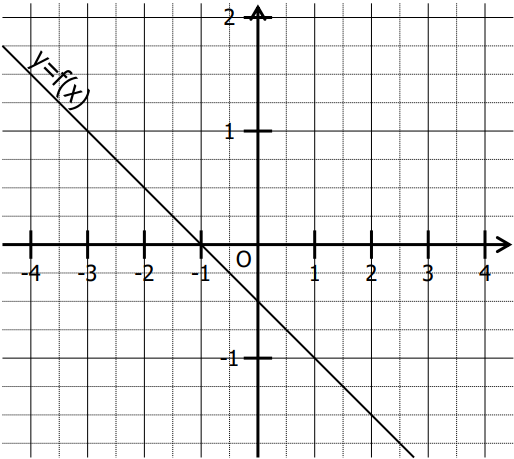
$1)$ Compléter en lisant sur le graphique :
$f(2) = ……$
$f(….) = 1$
$f(-2) = ….$
$f(…..) = \frac{3}{2}$
$f(-3) = …..$
$f(…..) = -\frac{5}{4}$
$2)$ Déterminer $f (0)$ et $f (1)$
$3)$ Déterminer l’expression de la fonction $f(x)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 12:
Le graphique ci-contre représente deux fonctions $f$ et $g$.
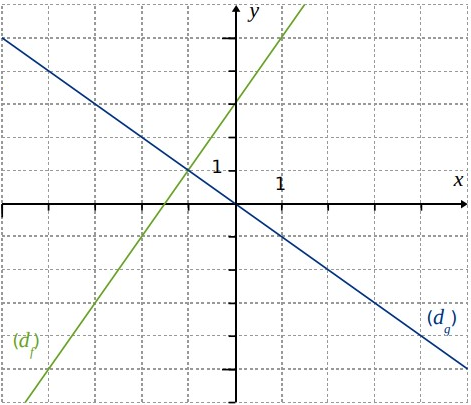
$1)$ Quelle est la nature de $f$ ? Trouve l’expression de $f$ en expliquant ta démarche.
$2)$ Quelle est la nature de $g$ ? Trouve l’expression de $g$ en expliquant ta démarche.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 13:
$1)$ On considère la fonction $h$ est définie par $h(x)=-5 x$.
$a)$ Détermine les images, par la fonction $h$, des nombres $-3$ et $\frac{1}{2,5}$.
$b)$ Calcule $h(-1)$ et $h(0,5)$.
$c)$ Détermine les antécédents, par la fonction $h$, des nombres $55 ;-\frac{10}{7}$.
$2)$ La fonction $g$ est définie par $g(x)=-3 x+1$.
$a)$ Quelle est l’image de $ 7$ par la fonction $g$ ?
$b)$ Détermine $g(0) ; g(-7)$.
$c)$Détermine les antécédents, par la fonction $g$ des nombres $-14$ et $0$ (justifie!).
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
Exercice 14:
Le plan est rapporté $d^{\prime}$ un repère orthonormé $(0, I, J)$.
On considère la fonction affine $f$ définie par : $f(x)=2 x-4$ et soit $\left(D_{1}\right)$ est sa représentation graphique dans le repère $(0, I, J)$.
$1)$ $a)$ Calcule $f(0)$ et $f(1)$
$b)$ Déterminer le nombre a qui a pour image 2 par $f$
$c)$ Le point $H(1 ; 2)$ appartient -il à $\left(D_{1}\right)$ ? justifie ta réponse
$d)$ Déterminer l’abscisse du point d’intersection de $\left(D_{1}\right)$ et l’axe des abscisses
$2)$ Soient g la fonction linéaire telle que sa représentation graphique $\left(D_{2}\right)$ passe par le point $P(-1 ; 2)$.
$a)$ Montre que : $g(x)=-2 x$
$b)$ Déterminer l’abscisse du point d’intersection de $\left(D_{1}\right)$ et $\left(D_{2}\right)$
$c)$ Construis $\left(D_{1}\right)$ et ( $D_{2}$ ) dans un même repère $(O, I, J)$.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 15 : Fonction affine
Considérons la fonction affine définie par :
\[ f(x) = 3x – 1. \]
1) Calculer les images de 0 et \(-2\) par la fonction \(f\).
2) Déterminer les nombres qui ont pour images 2 et 0 par la fonction \(f\).
3) Est-ce que A(1 ; 2) et B(-3 ; 10) appartiennent à (D) la représentation graphique de \(f\) ?
4) Construire (D).
5) a- Déterminer algébriquement le couple de coordonnées de H l’intersection de (D) et l’axe des abscisses.
b- Déterminer algébriquement le couple de coordonnées de M l’intersection de (D) et l’axe des ordonnées.
6) Soit \(g\) une fonction linéaire définie par \(g(x) = 5x\), et soit (L) sa représentation graphique. Déterminer algébriquement le couple de coordonnées du point P d’intersection de (L) et (D).
7) Déterminer \(a\) sachant que \(f(-5a + 2) = 2a\).
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
🚗Exercice 16: Location de voiture
Pour la location d’une voiture, on propose deux tarifs :
tarif 1 : \( 2 \, \text{Dhs/km} \)
tarif 2 : \( 500 \, \text{Dhs de réservation et } \, 1,5 \, \text{Dhs/km} \).
1) On désigne par \( x \) la distance parcourue (en \( \text{Km} \))
a- Exprimer \( f(x) \) la somme à payer en tarif 1 en fonction de \( x \).
b- Exprimer \( g(x) \) la somme à payer en tarif 2 en fonction de \( x \).
2) Quel tarif choisir, si on veut parcourir un trajet de \( 542 \, \text{km} \)?
3) A partir de quelle distance le tarif 2 est plus avantageux que le tarif 1 ?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 17: Figure géométrique
On considère la figure suivante composée par un demi-cercle et un carré de côté \( x \), et soit \( MN = 8 \).
On désigne par :
\( p(x) \) : le périmètre de la figure.
\( a(x) \) : l’aire de la figure.
\( p(x) \) et \( a(x) \) sont-elles des fonctions affines ?
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
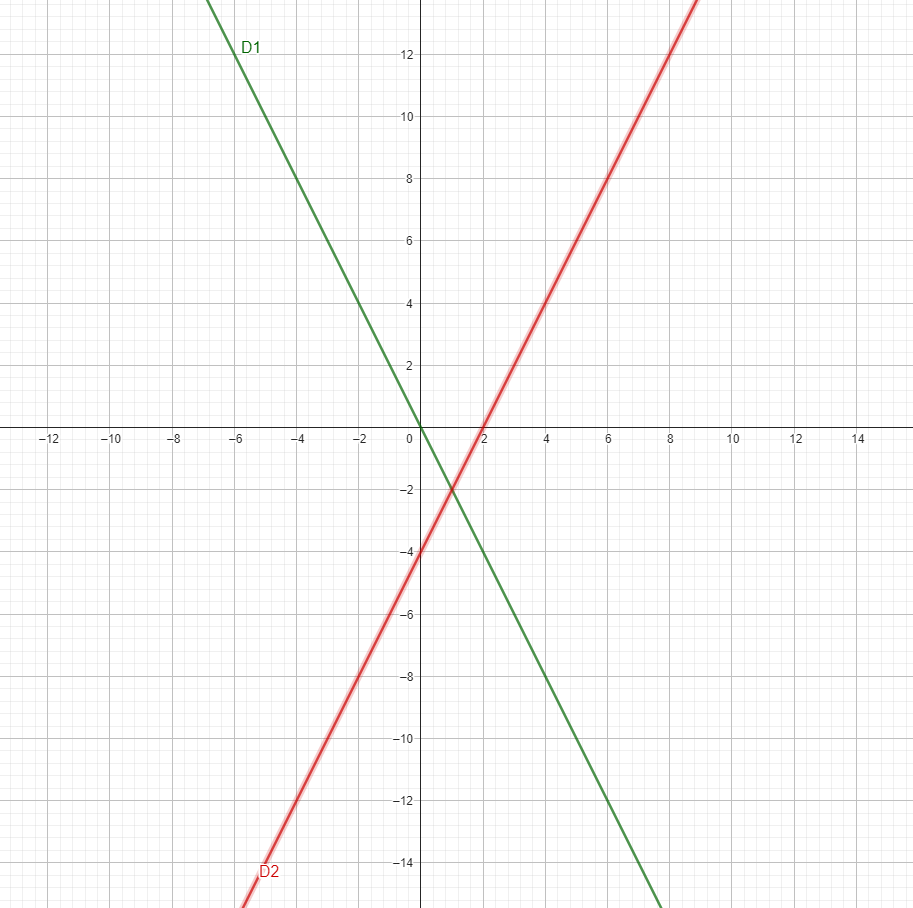
Fonction linéaire et fonction affine exercices corrigés