Généralités sur les fonctions exercices corrigés
Exercice 1:
Soit la fonction f de $\mathbb{R}$ dans $\mathbb{R}$ définie par: $f(x)=3 x^{2}-1$
$1)$ Calculer les images de 1 et $\sqrt{2}$ et -1 par $f$.
$2)$ Déterminer les antécédents éventuels de $2$ par $f$
$1)$ Calcul des images :
$f(1)=3 \times 1^{2}-1=3-1=2$
$f(\sqrt{2})=3 \times(\sqrt{2})^{2}-1=6-1=4$
$f(-1)=3 \times(-1)^{2}-1=3-1=2$
$2)$ $x$ est l’antécédents de $2$ par $f$ signifie que $2$ est l’image de $x$ par $f$
Chercher les réels $x$ tels que : $f(x)=2$
On résout alors dans $\mathbb{R}$ l’équation $f(x)=2$
Équivaut à: $\quad 3 \times x^{2}-1=2$
Équivaut à: $3 \times x^{2}=2+1$
Équivaut à: $\quad 3 \times x^{2}=3$
Équivaut à: $x^{2}=1$
Équivaut à: $\quad x=-1$ ou $x=1$
Finalement les antécédents de $ 2$ par $f$ sont $-1$ et $1$ .
Exercice 2:
Soit la fonction f de $\mathbb{R}$ dans $\mathbb{R}$ définie par : $f(x)=-x^{2}+2 x+2$
$1)$ Calculer les images de $\frac{-1}{2}$ et $\sqrt{3}$ par $f$.
$2)$ Montrer que : $1+\sqrt{2}$ est un antécédent de $1$ par $f$
$3)$ Déterminer les antécédents éventuels de $0$ par $f$
$4)$ Donner une interprétation géométrique du résultat de la question $(3)$
$1)$ Calcul des images :
$f\left(\frac{-1}{2}\right)=-\left(\frac{-1}{2}\right)^{2}+2 \times\left(\frac{-1}{2}\right)+2=-\frac{1}{4}-1+2=\frac{3}{4}$
$\quad f(\sqrt{3})=-(\sqrt{3})^{2}+2 \times(\sqrt{3})+2=-3+2 \sqrt{3}+2=-1+2 \sqrt{3}$
$2)$ Pour montrer que : $1+\sqrt{2}$ est un antécédents de 1 par f il suffit de montrer que : $f(1+\sqrt{2})=1$ ?
$f(1+\sqrt{2})=-(1+\sqrt{2})^{2}+2 \times(1+\sqrt{2})+2=-(1+2 \sqrt{2}+2)+2+2 \sqrt{3}+2$
$f(1+\sqrt{2})=-3-2 \sqrt{2}+2 \sqrt{2}+4=1$
Donc : $f(1+\sqrt{2})=1$ par suite : $1+\sqrt{2}$ est un antécédents de $1$ par $ f $.
$3)$ $x$ est l’antécédents de 0 par f signifie que 0 est l’image de $x$ par $f$ .
Équivaut à: chercher les réels $x$ tels que : $f(x)=0$
On résout alors dans $\mathbb{R}$ l’équation $f(x)=0$
Équivaut à: $-x^{2}+2 x+2=0$
$a=-1$ et $b=2$ et $c=2$
$\Delta=b^{2}-4 a c=2^{2}-4 \times 2 \times(-1)=4+8=12=(2 \sqrt{3})^{2}>0$
$x_{1}=\frac{-b+\sqrt{\Delta}}{2 a}$ et $x_{2}=\frac{-b-\sqrt{\Delta}}{2 a}$
$x_{1}=\frac{-2+2 \sqrt{3}}{-2}=1-\sqrt{3}$ et $x_{2}=\frac{-2-2 \sqrt{3}}{-2}=1+\sqrt{3}$
Finalement les antécédents de $0$ par $f$ sont: $1-\sqrt{3}$ et $1+\sqrt{3}$.
$4)$ Les antécédents éventuels de $0$ par $f$ sont : $1-\sqrt{3}$ et $1+\sqrt{3}$.
Donc: l’intersection de $\left(C_{f}\right)$ la courbe représentative de $f$ avec l’axe des abscisses sont les points : $A(1-\sqrt{3} ; 0)$ et $B(1+\sqrt{3} ; 0)$.
Exercice 3:
On considère la fonction réelle de la variable réelle définie par: $x \stackrel{\ddagger}{\mapsto} \frac{1}{\mathrm{x}-3}$
Parmi les valeurs suivantes, laquelle/lesquelles n’a/ont pas d’image par f ? $0 ; 2 ;-3 ; 3$.
$0 ; 2 ;-3$ ont des images par f mais $3$ n’a pas d’images par $f$ car : $f(3)=\frac{1}{3-3}=\frac{1}{0} \notin \mathbb{R}$
Exercice 4:
Déterminer l’ensemble de définition des fonctions suivantes définies par :
$a.$ $f(x)=x^{2}+4 x-5$
$b.$ $f(x)=\frac{2 x+1}{x}$
$c.$ $f(x)=\frac{3 x}{x^{2}-9}$
$d.$ $f(x)=\sqrt{x^{2}+1}$
$e.$ $f(x)=\sqrt{x^{2}+x+5}$
$f. $$f(x)=\sqrt{x}+\frac{1}{x-1}$
$g.$ $f(x)=\sqrt{x^{2}-x-2}$
$h.$ $f(x)=3-\sqrt{2-x}$
$i.$ $f(x)=\frac{2 x+1}{\sqrt{x^{2}-6 x+5}}$
$j. $$f(x)=\frac{1}{x-2}$
$a.$ $f(x)=x^{2}+4 x-5$
$D_{f}=\mathbb{R}$ ( car $f$ est une fonction polynôme)
$b.$ $f(x)=\frac{2 x+1}{x}$
$\left.D_{f}=\{x \in \mathbb{R} / x \neq 0\}=\mathbb{R}-\{0\}=\right]-\infty, 0[\cup] 0,+\infty[$
$c.$ $f(x)=\frac{3 x}{x^{2}-9}$
$D_{f} = \left\{x \in \mathbb{R} / x^{2}-9 \neq 0\right\}$
$ = \{x \in \mathbb{R} /(x-3)(x+3) \neq 0\} $
$ = \{x \in \mathbb{R} / x-3 \neq 0 \quad \text { et } \quad x+3 \neq 0\}$
$ = \{x \in \mathbb{R} / x \neq 3 \text { et } \quad x \neq-3\} $
$ = \mathbb{R}-\{-3,3\} $
$ = ]-\infty,-3[\cup]-3,3[\cup] 3,+\infty[$
$d.$ $f(x)=\sqrt{x^{2}+1}$
$D_{f}=\left\{x \in \mathbb{R} / x^{2}+1 \geq 0\right\}=\mathbb{R} \quad\left(\right.$ car pour tout $x$ de $\mathbb{R}$, on a : $\left.x^{2}+1>0\right)$
$e.$ $f(x)=\sqrt{x^{2}+x+5}$
$D_{f}=\left\{x \in \mathbb{R} / x^{2}+x+5 \geq 0\right\}$
Etudions le signe su polynôme $x^{2}+x+5$ :
On a : $\Delta=1^{2}-4(1)(5)=-19<0$

D’où : $D_{f}=\mathbb{R}$
$f.$ $\quad f(x)=\sqrt{x}+\frac{1}{x-1}$
$D_{f} = \{x \in \mathbb{R} / x \geq 0 \quad \text { et } \quad x-1 \neq 0\} $
$ = \{x \in \mathbb{R} / x \geq 0 \quad \text { et } \quad x \neq 1\} $
$ = {[0,1[\cup] 1,+\infty[ }$
$g.$ $f(x)=\sqrt{x^{2}-x-2}$
$D_{f}=\left\{x \in \mathbb{R} / x^{2}-x-2 \geq 0\right\}$
Etudions le signe su polynôme $x^{2}-x-2$ :
On a : $\Delta=(-1)^{2}-4(1)(-2)=9>0$
$x_{1}=\frac{-(-1)-\sqrt{9}}{2(1)} $ , $ x_{2}=\frac{-(-1)+\sqrt{9}}{2(1)} $
$x_{1}=-1 $ , $ x_{2}=2$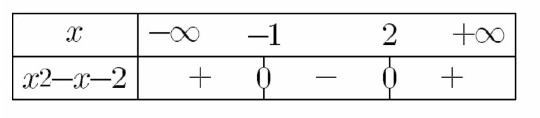
Donc : $\left.\left.D_{f}=\right]-\infty,-1\right] \cup[2,+\infty[$
$h.$ $f(x)=3-\sqrt{2-x}$
$\left.\left.D_{f}=\{x \in \mathbb{R} / 2-x \geq 0\}=\{x \in \mathbb{R} / x \leq 2\}=\right]-\infty, 2\right]$
$i.$ $f(x)=\frac{2 x+1}{\sqrt{x^{2}-6 x+5}}$
$D_{f}=\left\{x \in \mathbb{R} / x^{2}-6 x+5>0\right\}$
Etudions le signe su polynôme $x^{2}-6 x+5$ :
On a : $\Delta=(-6)^{2}-4(1)(5)=16>0$
$x_{1}=\frac{-(-6)-\sqrt{16}}{2(1)} $ , $ x_{2}=\frac{-(-6)+\sqrt{16}}{2(1)} $
$x_{1}=1$, $ x_{2}=5$
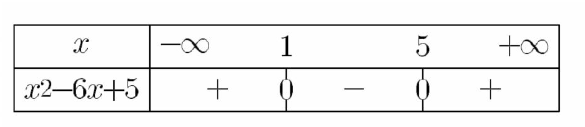
Donc : $\left.D_{f}=\right]-\infty, 1[\cup] 5,+\infty[$
$j.$ $\quad f(x)=\frac{1}{x-2}$
$\left.D_{f}=\{x \in \mathbb{R} / x-2 \neq 0\}=\{x \in \mathbb{R} / x \neq 2\}=\right]-\infty, 2[\cup] 2,+\infty[$
Exercice 5:
Déterminer l’ensemble de définition des fonctions suivantes définies par :
$1)$ $f(x)=\frac{2 \sin x}{2 \cos x-1}$
$2)$ $f(x)=\frac{2 \cos x}{2 \sin x+1}$
$3)$ $f(x)=\frac{2 \sin x}{\tan x-\sqrt{3}}$
$4)$ $f(x)=\frac{2 \sin ^{2} x}{\sin (2 x)-\cos (3 x)}$
$1)$ $f(x)=\frac{2 \sin x}{2 \cos x-1}$.
$D_{f}=\{x \in \mathbb{R} / 2 \cos x-1 \neq 0\}$
$2 \cos x-1=0$ Signifie $\cos x=\frac{1}{2}$
c’est-à-dire $\cos x=\cos \left(\frac{\pi}{3}\right)$
Signifie que : $x=\frac{\pi}{3}+2 k \pi$ ou $x=-\frac{\pi}{3}+2 k \pi$
Où $k \in \mathbb{Z}$ Donc: $D_{f}=\mathbb{R}-\left\{-\frac{\pi}{3}+2 k \pi ; \frac{\pi}{3}+2 k \pi / k \in \mathbb{Z}\right\}$
$2)$ $f(x)=\frac{2 \cos x}{2 \sin x+1} . \quad D_{f}=\{x \in \mathbb{R} / 2 \sin x+1 \neq 0\}$
$2 \sin x+1=0$ Signifie $\sin x=-\frac{1}{2}$
Signifie que: $\sin x=-\sin \left(\frac{\pi}{6}\right)$
Donc: $\sin x=\sin \left(-\frac{\pi}{6}\right)$
Signifie $\quad x=-\frac{\pi}{6}+2 k \pi$ ou $x=\pi-\left(-\frac{\pi}{6}\right)+2 k \pi$
Signifie $\quad x=-\frac{\pi}{6}+2 k \pi$ ou $x=\frac{7 \pi}{6}+2 k \pi$ où $k \in \mathbb{Z}$
Donc: $D_{f}=\mathbb{R}-\left\{-\frac{\pi}{6}+2 k \pi ; \frac{7 \pi}{6}+2 k \pi / k \in \mathbb{Z}\right\}$
$3)$ $f(x)=\frac{2 \sin x}{\tan x-\sqrt{3}}$.
$D_{f}=\left\{x \in \mathbb{R} / x \neq \frac{\pi}{2}+k \pi\right.$ et $\left.\tan x-\sqrt{3} \neq 0 / k \in \mathbb{Z}\right\}$ $\tan x-\sqrt{3}=0$ Signifie $\tan x=\sqrt{3}$
C’est-à-dire $\tan x=\tan \left(\frac{\pi}{3}\right)$
Signifie $\quad x=\frac{\pi}{3}+k \pi$ où $k \in \mathbb{Z}$
Donc: $D_{f}=\mathbb{R}-\left\{\frac{\pi}{2}+k \pi ; \frac{\pi}{3}+k \pi / k \in \mathbb{Z}\right\}$
$4)$ $f(x)=\frac{2 \sin ^{2} x}{\sin (2 x)-\cos (3 x)}$
$D_{f}=\{x \in \mathbb{R} / \sin (2 x)-\cos (3 x) \neq 0\}$
On a: $\sin (2 x)-\cos (3 x)=0$
Équivaut à : $\sin (2 x)=\cos (3 x)$
C’est-à-dire : $\sin (2 x)=\sin \left(\frac{\pi}{2}-3 x\right)$
Équivaut à : $2 x=\frac{\pi}{2}-3 x+2 k \pi$ ou $2 x=\pi-\left(\frac{\pi}{2}-3 x\right)+2 k \pi$ et $k \in \mathbb{Z}$.
Équivaut à : $5 x=\frac{\pi}{2}+2 k \pi$ ou $-x=\frac{\pi}{2}+2 k \pi$
C’est-à-dire : $x=\frac{\pi}{10}+\frac{2 k \pi}{5}$ ou $x=-\frac{\pi}{2}+2 k \pi$
Donc: $D_{f}=\mathbb{R}-\left(\left\{\frac{\pi}{10}+\frac{2 k \pi}{5} / k \in \mathbb{Z}\right\} \cup\left\{-\frac{\pi}{2}+2 k \pi / k \in \mathbb{Z}\right\}\right)$
Exercice 6:
Soient les deux fonctions $h(x)=\frac{x^{2}-x}{x}$ et $t(x)=x-1$
Est-ce que : $\mathrm{h}=\mathrm{t}$. ? Justifier
– On a : $h(x) \in \mathbb{R}$ signifie que : $x \neq 0$
Donc $D_{h}=\mathbb{R}^{*}$
– On a $t(x)$ est un polynôme
Donc $D_{t}=\mathbb{R}$
Alors: $D_{h} \neq D_{t}$
Donc: $h \neq t$
Exercice 7:
Soient les deux fonctions $f(x)=\frac{3 x^{2}+1}{\sqrt{x^{2}}}$ et $g(x)=\frac{1+3 x^{2}}{|x|}$
Est-ce que : $f=g$. ? Justifier
– On a : $f(x) \in \mathbb{R}$ signifie $\sqrt{x^{2}} \in \mathbb{R}$ et $x \neq 0$
Or on sait que $x^{2} \geq 0$ donc $\sqrt{x^{2}} \in \mathbb{R}$ pour tout $x \in \mathbb{R}$
Alors : $f(x) \in \mathbb{R}$ signifie que : $x \neq 0$
Donc: $D_{f}=\mathbb{R}^{*}$
– On a $g(x) \in \mathbb{R}$ signifie que : $|x| \neq 0$
-C’est-à-dire : $x \neq 0$ Donc : $D_{g}=\mathbb{R}^{*}$
Alors : $D_{f}=D_{g}=\mathbb{R}^{*}$
On sait que : $\sqrt{x^{2}}=|x|$ et $3 x^{2}+1=1+3 x^{2}$
Donc: $f(x)=g(x)$.
Donc finalement on a trouvé que : $D_{f}=D_{g}=\mathbb{R}^{*}$ et $f(x)=g(x)$
Par suite : $f=g$.
Exercice 8:
Les fonctions $f$ et $g$ définies respectivement par :
$f(x)=\sqrt{\frac{x-1}{x+3}} \text { et } g(x)=\frac{\sqrt{x-1}}{\sqrt{x+3}}$. Sont-elles égales?
Déterminons leur ensemble de définition
Pour f , on doit avoir : $\frac{x-1}{x+3} \geq 0$ et $x-1 \neq 0$
Donc ce qui donne : $\left.D_{f}=\right]-\infty ;-3[\cup[1 ;+\infty[$
Pour g, on doit avoir $x-1 \geq 0$ et $x+3 \succ 0$
Ce qui donne $D_{g}=[1 ;+\infty[$
On a donc: $D_{f} \neq D_{g}$.
Les fonctions ne sont donc pas égales.
Exercice 9:
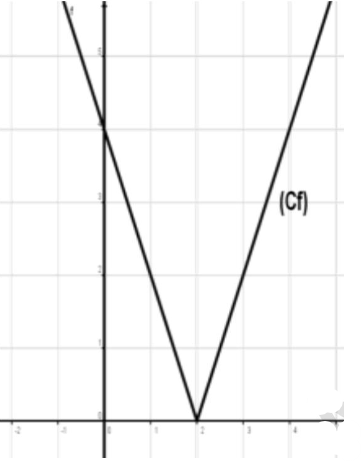
Tracer la représentation graphique de la fonction f tel que: $f(x)=|2 x-4|$
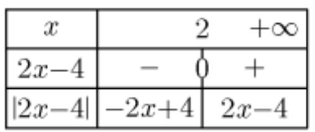
On a $f(x) \in \mathbb{R}$ donc $D_{f}=\mathbb{R}$
$2 x-4=0$ Équivaut à: $x=\frac{4}{2}=2$
Donc $f(x)=2 x-4$ si $x \in[2,+\infty[$
Et $f(x)=-2 x+4$ si $x \in]-\infty, 2]$
Exercice 10:
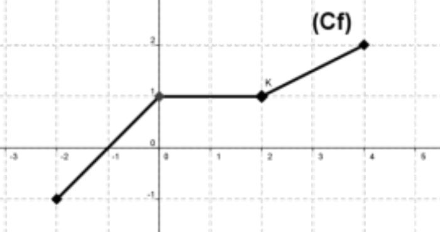
$1)$ Déterminer les images des nombres: $-2;-1;0;2;4$ par la fonction f .
$2)$ Déterminer : $f(x)$ en fonction de $x$ sur $[-2,4]$
$1)$ $f(-2)=-1$ et $f(-1)=0$ et $f(0)=1$ et $f(2)=1$ et $f(4)=2$
$2)$ On remarque que la représentation graphique de la fonction f est un segment sur chacun des intervalles : $[-2,0]$ et $[0,2]$ et $[2,4]$
Donc la fonction f est affine sur ces intervalles
– Sur l’intervalle $[-2,0]$ on a : $f(x)=a_{1} x+b_{1}$
– Et on a : $f(-2)=-1$ et $f(-1)=0$
Donc: $\left\{\begin{array}{l}-2 a_{1}+b_{1}=-1 \\ -a_{1}+b_{1}=0\end{array}\right.$
C’est-à-dire : $\left\{\begin{array}{l}-a_{1}=-1 \\ b_{1}=a_{1}\end{array}\right.$
Donc: : $\left\{\begin{array}{l}a_{1}=1 \\ b_{1}=1\end{array}\right.$
Par suite : $f(x)=x+1$
– Sur l’intervalle $[0,2]$ on a : $f(x)=1$
– Sur l’intervalle $[2,4]$ on a : $f(x)=a_{2} x+b_{2}$
– Et on a: $f(2)=1$ et $f(4)=2$
Donc: $\left\{\begin{array}{l}2 a_{2}+b_{2}=1 \\ 4 a_{2}+b_{2}=2\end{array}\right.$
C’est-à-dire : $\left\{\begin{array}{l}2 a_{2}=1 \\ b_{2}=2-4 a_{2}\end{array}\right.$
Donc : $\left\{\begin{array}{l}a_{2}=\frac{1}{2} \\ b_{2}=2-2=0\end{array} \quad\right.$
Par suite : $f(x)=\frac{1}{2} x$
Par conséquent :$\left\{\begin{array}{l}f(x)=x+1 \quad \text { si } x \in[-2,0] \\f(x)=1 \quad \text { si } x \in[0,2] \\f(x)=\frac{1}{2} x \quad \text { si } x \in[2,4]\end{array} \quad\right.$
Exercice 11:
La courbe ci-dessous représente la fonction $f$ définie sur $[-6 ; 7]$
Répondre par lecture graphique :
$1)$ Quelles sont les images des réels $-5,-3,0$ et 6 ?
$2)$ Quels sont les antécédents de -1 et 0 ?
$3)$ Résoudre graphiquement $f(x)=0$
$4)$ Quel est en fonction de $m$ le nombre de solutions de : $f(x)=m$.
$5)$ Résoudre graphiquement $f(x) \prec 0$
$6)$ Résoudre graphiquement $f(x) \geq 2$
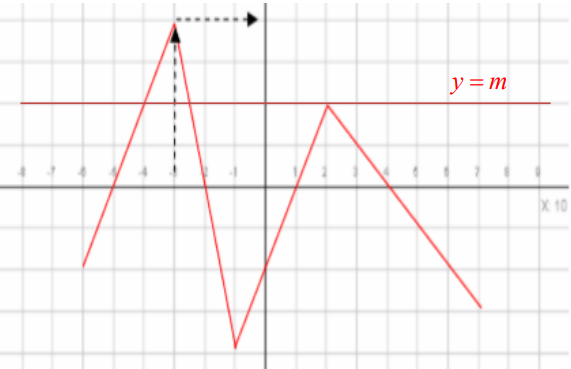
$1)$ Image de $-5$ est $0$ (ordonnée du point d’abscisse $-5$)
Image de $-3$ est $4$ et l’image de $0$ est $-2$ et l’image de $6$ est $-2$
$2)$ Antécédents de -1 sont: $-5,5 ;-1,75 ; 0,5$ et $5$ et Antécédents de 0 sont: $-5 ;-2 ; 1$ et $4$ .
$3)$ L’ensemble des solutions est l’ensemble des antécédents de $0: S=\{-5 ;-2 ; 1 ; 4\}$
$4)$ Nombre de solutions de $f(x)=m$ c’est le nombre de points d’intersections de la courbe avec la droite parallèle à l’axes des abscisses et d’ordonnées $m$.
Si $m \prec-4$ : pas de solution
Si $m=-4$ : une solution
Si: $-4 \prec m \prec-3$ deux solutions
Si $-3 \prec m \prec-2$ : trois solutions
Si $-2 \prec m \prec 2$ : quatre solutions
Si $m=2$ : trois solutions
Si: $2 \prec m \prec 4$ deux solutions
Si $m=4$ :une solution
Si $m \succ 4$ : pas de solution
$5)$ $f(x) \prec 0$ Cela correspond aux valeurs de x pour lesquelles $C_{f}$ est au-dessous de l’axe des abscisses. $S=[-6 ; 7] \cup]-2 ; 1[\cup] 4 ; 7]$
$6)$ $f(x) \geq 2$ Cela correspond aux valeurs de $x$ pour lesquelles $C_{f}$ est au-dessus de la droite d’équation $y=2 \quad$
Donc $S=[-4 ; 2.5] \cup\{2\}$
Exercice 12:
Soit f et g deux fonctions définies sur $\mathbb{R}$ par: $f(x)=x^{2}-2 x-5$ et $g(x)=-x-3$.
Étudier les positions de $\left(C_{f}\right)$ et $\left(C_{g}\right)$ les courbes représentatives respectives de $f$ et $g$
Soit $\mathrm{h}(\mathrm{x})=\mathrm{f}(\mathrm{x})-\mathrm{g}(\mathrm{x})$
Donc : $h(x)=x^{2}-2 x-5+x+3=x^{2}-x-2$
$h$ est une fonction du second degré.
Calculons son discriminant afin de déterminer son signe: $a=1, b=-1$ et $c=-2$.
$\Delta=(-1)^{2}-[4 \times 1 \times(-2)]=9=3^{2}$
$\Delta$ étant strictement positif, le trinôme admet deux racines qui sont : $x_{1}=\frac{1+3}{2 \times 1}=2$ et $\quad x_{2}=\frac{1-3}{2 \times 1}=-1$
Le signe de la fonction est du signe de a, c’est-à-dire positif de part et d’autre des racines mais du signe contraire (donc négatif) entre ces racines.
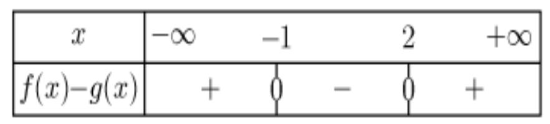
Par conséquent $\left(C_{f}\right)$ est confondue avec $\left(C_{g}\right)$
pour: $x=-1$ et $x=2$
$\left(C_{f}\right)$ Est située au-dessus de $\left(C_{g}\right)$ sur : $]-\infty ;-1[\cup] 2 ;+\infty[$
$\left(C_{f}\right)$ Est située au-dessus de $\left(C_{g}\right)$ sur $]-1 \infty ; 2[$
Exercice 13:
Etudier la parité des fonctions suivantes définie par :
$1)$ $f(x)=\frac{x^{2}-1}{x}$
$2)$ $f(x)=x^{2}+2 x+\frac{1}{x}$
$3)$ $f(x)=\frac{|x|}{x^{2}-1}$
$4)$ $f(x)=\sqrt{1-x^{2}}$
$5)$ $f(x)=\frac{2 x^{3}}{x^{2}+5}$
$6)$ $f(x)=|x|-\sqrt{2 x^{2}+4}$
$7)$ $f(x)=\frac{\sqrt{x}}{2}$
$8)$ $f(x)=\frac{x}{x-2}$
$9)$ $g(x)=\frac{2 \sin x}{1-\cos x}$
$1)$ $f(x)=\frac{x^{2}-1}{x} \quad$ On a $f(x) \in \mathbb{R}$
Signifie que : $x \neq 0 \quad$ par suite : $D_{f}=\mathbb{R}^{*}$
Pour tout réel x , si $x \in \mathbb{R}^{*}$, alors $-x \in \mathbb{R}^{*}$
$f(-x)=\frac{(-x)^{2}-1}{-x}=-\frac{x^{2}-1}{x} $
$ f(-x)=-f(x)$
Donc $f$ est une fonction impaire.
$2)$ $f(x)=x^{2}+2 x+\frac{1}{x} \quad$ on a $f(x) \in \mathbb{R}$
Signifie $\quad x \neq 0 \quad$ Donc: $D_{f}=\mathbb{R}^{*}$
$\mathbb{G}^{2}$ Pour tout réel x , si $x \in \mathbb{R}^{*}$
Alors $-x \in \mathbb{R}^{*}$
$f(-x)=(-x)^{2}+2(-x)+\frac{1}{-x}=x^{2}-2 x-\frac{1}{x}$
$f(-x) \neq-f(x)$
Donc $f$ est une fonction ni paire ni impaire.
$3)$ $f(x)=\frac{|x|}{x^{2}-1}$
On a: $f(x) \in \mathbb{R}$ signifie $x^{2}-1 \neq 0$
$x^{2}-1=0$ Signifie $x^{2}=1$
Équivaut à: $x=1$ ou $x=-1$
Donc $D_{f}=\mathbb{R}-\{-1 ; 1\}$
Pour tout réel x , si $x \in \mathbb{R}-\{-1 ; 1\}$
Alors : $-x \in \mathbb{R}-\{-1 ; 1\}$
$f(-x)=\frac{|-x|}{(-x)^{2}-1}=\frac{|x|}{x^{2}-1}$
$f(-x)=f(x) \quad$ Donc $f$ est une fonction paire
$4)$ $f(x)=\sqrt{1-x^{2}} . \quad D_{f}=\left\{x \in \mathbb{R} / 1-x^{2} \geq 0\right\}$
$1-x^{2}=0$ Signifie $x^{2}=1$ Équivaut à: $x=1$ ou $x=-1$
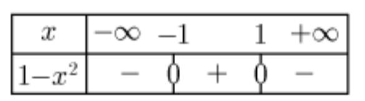
Donc $D_{f}=[-1,1]$
Pour tout réel x , si $x \in[-1,1]$ alors $-x \in[-1,1]$
$f(-x)=\sqrt{1-(-x)^{2}}=\sqrt{1-x^{2}}$
$f(-x)=f(x)$
Donc $f$ est une fonction paire
$5)$ $f(x)=\frac{2 x^{3}}{x^{2}+5} . \quad D_{f}=\left\{x \in \mathbb{R} / x^{2}+5 \neq 0\right\}$
$x^{2}+5=0$ Signifie : $x^{2}=-5$ pas de solutions
Donc $D_{f}=\mathbb{R}$
Pour tout réel x si $x \in \mathbb{R}$, alors $-x \in \mathbb{R}$
$f(-x)=\frac{2(-x)^{3}}{(-x)^{2}+5}=\frac{-2 x^{3}}{x^{2}+5}$
$f(-x)=-f(x)$
Donc $f$ est une fonction impaire
$6)$ $f(x)=|x|-\sqrt{2 x^{2}+4}$.
$D_{f}=\left\{x \in \mathbb{R} / 2 x^{2}+4 \geq 0\right\} \quad$
Or on sait que $2 x^{2} \geq 0$
Pour tout réel $x$, donc $2 x^{2}+4 \geq 0+4$
Par suite $2 x^{2}+4 \geq 4 \geq 0 \quad$
Donc $D_{f}=\mathbb{R}$
${ }^{2}$ Pour tout réel $x$, si $x \in \mathbb{R}$, alors $-x \in \mathbb{R}$
$f(-x)=|-x|-\sqrt{2(-x)^{2}+4}=|x|-\sqrt{2 x^{2}+4}$
$f(-x)=f(x)$
Donc $f$ est une fonction paire.
$7)$ $f(x)=\frac{\sqrt{x}}{2} . \quad D_{f}=\{x \in \mathbb{R} / x \geq 0\}$
Donc $D_{f}=\mathbb{R}^{+}=[0 ;+\infty[$
On a $2 \in \mathbb{R}^{+}$mais $-2 \notin \mathbb{R}^{+}$
donc $f$ est une fonction ni paire ni impaire
$8)$ $f(x)=\frac{x}{x-2}$ : On a $f(x) \in \mathbb{R}$
Signifie $x-2 \neq 0$ c’est-à-dire : $x \neq 2$
Donc $D_{f}=\mathbb{R}-\{2\}$
On a $-2 \in D_{f}$ mais $-(-2)=2 \notin D_{t}$
Donc: $D_{f}$ n’est pas symétrique par rapport a $O$
Donc: $f$ est une fonction ni paire ni impaire
$9)$ $g(x)=\frac{2 \sin x}{1-\cos x} . \quad D_{g}=\{x \in \mathbb{R} / 1-\cos x \neq 0\}$
$1-\cos x=0$ Signifie $\cos x=1$
C’est-à-dire : $x=0+2 k \pi$ où $k \in \mathbb{Z}$
Donc: $D_{g}=\mathbb{R}-\{2 k \pi / k \in \mathbb{Z}\}$
Pour tout réel $x$, si $x \in \mathbb{R}-\{2 k \pi / k \in \mathbb{Z}\}$
Alors : $-x \in \mathbb{R}-\{2 k \pi / k \in \mathbb{Z}\}$
(-x) $g(-x)=\frac{2 \sin (-x)}{1-\cos (-x)}=\frac{-2 \sin x}{1-\cos x}=-\frac{2 \sin x}{1-\cos x}=-g(x)$
Car $\cos (-x)=\cos x$ et $\sin (-x)=-\sin x$ si $x \in \mathbb{R}$
Donc $g$ est une fonction impaire
Exercice 14:
Soit la fonction définie par : $f(x)=\frac{|x|+1}{2|x|-3}$
$\left(C_{f}\right)$ la courbe de $f$ Dans le repère $(0 ; \vec{i} ; \vec{j})$ orthonormé.
Montrer que $\left(C_{f}\right)$ symétrique par rapport à l’axe des ordonnées
$D_{f}=\{x \in \mathbb{R} / 2|x|-3 \neq 0\}=\left\{x \in \mathbb{R} /|x| \neq \frac{3}{2}\right\}$
Donc: $D_{f}=\mathbb{R}-\left\{-\frac{3}{2} ; \frac{3}{2}\right\}$
Il suffit de montrer que : $f$ est une fonction paire Pour tout réel $x$, si $x \in \mathbb{R}-\left\{-\frac{3}{2} ; \frac{3}{2}\right\}$
Alors $-x \in \mathbb{R}-\left\{-\frac{3}{2} ; \frac{3}{2}\right\}$
$f(-x)=\frac{|-x|+1}{2|-x|-3}=\frac{|x|+1}{2|x|-3}=f(x)$
Donc $f$ est une fonction paire
Par suite : la $\left(C_{f}\right)$ est symétrique par rapport à
l’axe des ordonnées
Exercice 15:
Soient les fonctions définies par :
$1)$ $f(x)=7 x-5$
$2)$ $g(x)=\frac{2}{x}$
Etudier la monotonie de $f$ et de $g$ ?
$1)$ $f$ est une fonction polynôme
Donc: $D_{f}=\mathbb{R}$
Soit $x_{1} \in \mathbb{R}$ et $x_{2} \in \mathbb{R}$ tels que: $x_{1} \prec x_{2}$
Donc $7 x_{1} \prec 7 x_{2}$ car $7 \succ 0$
Donc $7 x_{1}-5 \prec 7 x_{2}-5$ Alors $f\left(x_{1}\right) \prec f\left(x_{2}\right)$
D’où $f$ est strictement croissante sur $\mathbb{R}$
$2)$ Soit $g$ une fonction tel que : $g(x)=\frac{2}{x}$
$g(x) \in \mathbb{R}$ Signifie $x \neq 0 \quad$
Donc $D_{g}=\mathbb{R}-\{0\}=\mathbb{R}^{*}$
• Soit $x_{1} \in\left[0 ;+\infty\left[\right.\right.$ et $x_{2} \in[0 ;+\infty[$ tels que : $x_{1} \prec x_{2} \quad$
Donc $\frac{1}{x_{1}} \succ \frac{1}{x_{2}}$
Par suite : $\frac{2}{x_{1}} \succ \frac{2}{x_{2}}$ car $2 \succ 0$
Alors $f\left(x_{1}\right) \succ f\left(x_{2}\right)$ d’où $f$ est strictement décroissante sur $[0 ;+\infty[$
• Soit $\left.\left.x_{1} \in\right]-\infty ; 0\right]$ et $\left.\left.x_{2} \in\right]-\infty ; 0\right]$ tq $x_{1} \prec x_{2}$
Donc $\frac{1}{x_{1}} \succ \frac{1}{x_{2}}$
Par suite : $\frac{2}{x_{1}} \succ \frac{2}{x_{2}}$ car $2 \succ 0$
Alors : $f\left(x_{1}\right) \succ f\left(x_{2}\right)$ d’où f que est strictement décroissante sur ]- $\infty$; 0 ]
• Tableau de variation :
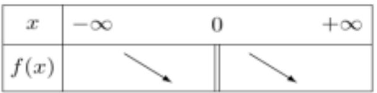
Exercice 16:
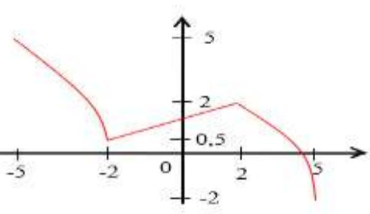
Soit la fonction définie par la représentions graphique suivante sur l’intervalle : $[-5 ; 5]$
Exercice 17:
Soit $f$ une fonction tel que : $f(x)=3 x^{2}+2$
$1)$ Déterminer $D_{f}$
$2)$ Calculer le taux d’accroissement de fonction de $f$ Entre $x_{1}$ et $x_{2}$ tel que : $x_{1} \neq x_{2}$
$3)$ Etudier les variations de $f$ sur les intervalles $[0 ;+\infty[$ et $]-\infty ; 0]$
$4)$ Dresser le tableau de variation de $f$
$1)$ $f$ est une fonction polynôme
Donc $D_{f}=\mathbb{R}$
$2)$ Soient $x_{1} \in \mathbb{R}$ et $x_{2} \in \mathbb{R}$ tel que : $x_{1} \neq x_{2}$
$T\left(x_{1} ; x_{2}\right)=\frac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}=\frac{\left(3 x_{1}^{2}+2\right)-\left(3 x_{2}{ }^{2}+2\right)}{x_{1}-x_{2}}$
$T\left(x_{1} ; x_{2}\right)=\frac{3 x_{1}^{2}-3 x_{2}^{2}+2-2}{x_{1}-x_{2}}=\frac{3\left(x_{1}^{2}-x_{2}^{2}\right)}{x_{1}-x_{2}}$
$T\left(x_{1} ; x_{2}\right)=\frac{3\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}\right)}{x_{1}-x_{2}}=3\left(x_{1}+x_{2}\right)$
$3)$ Soient $x_{1} \in \mathbb{R}$ et $x_{2} \in \mathbb{R}$ tels que: $\quad x_{1} \neq x_{2}$
On a: $\quad T\left(x_{1} ; x_{2}\right)=3\left(x_{1}+x_{2}\right)$
$a)$ Soit $x_{1} \in\left[0 ;+\infty\left[\right.\right.$ et $x_{2} \in[0 ;+\infty[$
Donc $x_{1} \geq 0$ et $x_{2} \geq 0$ et $x_{1} \neq x_{2}$
implique $x_{1}+x_{2} \succ 0$
Donc $3\left(x_{1}+x_{2}\right) \succ 0$ car $3 \succ 0$
Donc $T\left(x_{1} ; x_{2}\right)=3\left(x_{1}+x_{2}\right) \succ 0$
D’où : f est strictement croissante sur $[0 ;+\infty[$
$b)$ Soit $\left.\left.x_{1} \in\right]-\infty ; 0\right]$ et $\left.x_{2} \in\right]-\infty ; 0$ ]
Donc $x_{1} \leq 0$ et $x_{2} \leq 0$ et on a $x_{1} \neq x_{2}$
Donc : $x_{1}+x_{2} \prec 0$ par suite : $3\left(x_{1}+x_{2}\right) \prec 0$
car $3 \succ 0$
Donc $T\left(x_{1} ; x_{2}\right)=3\left(x_{1}+x_{2}\right) \prec 0$
D’où f est strictement décroissante sur $]-\infty ; 0$ ]
$4)$ Résumé : Tableau de variation :
$f(0)=3 \times 0^{2}+2=2$
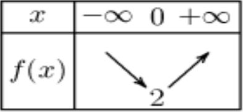
Exercice 18:
Soit $f$ une fonction numérique tel que : $f(x)=x^{2}+3 x+1$
$1)$ Préciser le domaine de définition de $f$
$2)$ Montrer que f est strictement croissante sur $\left[\frac{-3}{2} ;+\infty[\right.$et strictement décroissante sur $\left.]-\infty ; \frac{-3}{2}\right]$
$3)$ Dresser le tableau de variation de $f$
$4)$ $a)$ En déduire que : pour tout $x \in[-1 ; 3]$
On a : $-1 \leq f(x) \leq 19$
$b)$ En déduire que : pour tout $x \in[-5 ;-2]$
On a : $-1 \leq f(x) \leq 11$
$1)$ $f$ est une fonction polynôme
Donc $D_{f}=\mathbb{R}$.
$2)$ Soient $x_{1} \in \mathbb{R}$ et $x_{2} \in \mathbb{R}$ tel que : $x_{1} \neq x_{2}$
$T\left(x_{1} ; x_{2}\right)=\frac{f\left(x_{1}\right)-f\left(x_{2}\right)}{x_{1}-x_{2}}=\frac{\left(x_{1}^{2}+3 x_{1}+1\right)-\left(x_{2}^{2}+3 x_{2}+1\right)}{x_{1}-x_{2}}$
$T\left(x_{1} ; x_{2}\right)=\frac{x_{1}^{2}-x_{2}^{2}+3\left(x_{1}-x_{2}\right)}{x_{1}-x_{2}}=\frac{\left(x_{1}-x_{2}\right)\left(x_{1}+x_{2}+3\right)}{x_{1}-x_{2}}$
Donc : $T\left(x_{1} ; x_{2}\right)=x_{1}+x_{2}+3$
Par suite : Si : $x_{1} \in\left[\frac{-3}{2} ;+\infty\left[\right.\right.$ et $x_{2} \in\left[\frac{-3}{2} ;+\infty[\right.$
Alors $\quad x_{1} \geq \frac{-3}{2}$ et $x_{2} \geq \frac{-3}{2}$ et $x_{1} \neq x_{2}$
implique $x_{1}+x_{2} \succ-3$
Donc $x_{1}+x_{2}+3 \succ 0$ par suite : $T\left(x_{1} ; x_{2}\right) \succ 0$
D’où : $f$ est strictement croissante sur $\left[\frac{-3}{2} ;+\infty[\right.$
Si : $\left.\left.x_{1} \in\right]-\infty ; \frac{-3}{2}\right]$ et $\left.\left.x_{2} \in\right]-\infty ; \frac{-3}{2}\right]$
Alors : $\quad x_{1} \leq \frac{-3}{2}$ et $x_{2} \leq \frac{-3}{2}$ et $x_{1} \neq x_{2}$
Cela implique $\quad x_{1}+x_{2} \prec-3$
Donc $x_{1}+x_{2}+3 \prec 0$ par suite : $T\left(x_{1} ; x_{2}\right) \prec 0$
D’où : f est strictement décroissante sur $\left.]-\infty ; \frac{-3}{2}\right]$
$3)$ Tableau de variation :
On a : $f\left(\frac{-3}{2}\right)=\left(\frac{-3}{2}\right)^{2}+3\left(\frac{-3}{2}\right)+1=\frac{-5}{4}$
Donc :
$4)$ $a)$ Puisque f est strictement croissante sur $\left[\frac{-3}{2} ;+\infty[\right.$
Alors f est strictement croissante sur $[-1 ; 3] \quad$ Car $:[-1 ; 3] \subset\left[\frac{-3}{2} ;+\infty[\right.$
Si on a $x \in[-1 ; 3]$ alors : $f(-1) \leq f(x) \leq f(3)$ (f est strictement croissante)
On a : $f(-1)=(-1)^{2}+3(-1)+1=1-3+1=-1$ et $f(3)=3^{2}+3 \times 3+1=9+9+1=19$
Par suite : $-1 \leq f(x) \leq 19$ si $x \in[-1 ; 3]$
$b)$ Puisque f est strictement décroissante sur] $\left.-\infty ; \frac{-3}{2}\right]$ alors f est strictement croissante sur $x \in[-5 ;-2] \quad$ car $\left.:[-5 ;-2] \subset]-\infty ; \frac{-3}{2}\right]$
Si on a $x \in[-5 ;-2]$ alors : $f(-2) \leq f(x) \leq f(-5)$ (f est strictement décroissante)
On a : $f(-2)=(-2)^{2}+3(-2)+1=4-6+1=-1$ et $f(-5)=(-5)^{2}+3(-5)+1=25-15+1=11$
Par suite : $-1 \leq f(x) \leq 11$ si $x \in[-5 ;-2]$
Exercice 19:
Soit $g$ une fonction tel que : $g(x)=\frac{x}{x+1}$.
$1)$ Déterminer $D_{g}$.
$2)$ Calculer le taux d’accroissement de fonction de $g$ entre $x_{1}$ et $x_{2}$ tel que: $x_{1} \neq x_{2}$.
$3)$ Etudier les variations de $g$ sur les intervalles $I=]-\infty ;-1[$ et $J=]-1 ;+\infty[$.
$4)$ Dresser son tableau de variation de $f$.
$1)$ On a $g(x) \in \mathbb{R}$ équivaut à: $x+1 \neq 0$ c’est-à-dire : $x \neq-1 \quad$
Donc $D_{g}=\mathbb{R}-\{-1\}$
$2)$ Soient $x_{1} \in D_{g}$ et $x_{2} \in D_{g}$ tel que : $x_{1} \neq x_{2}$
On a: $T\left(x_{1} ; x_{2}\right)=\frac{g\left(x_{1}\right)-g\left(x_{2}\right)}{x_{1}-x_{2}}$
$g\left(x_{1}\right)-g\left(x_{2}\right)=\frac{x_{1}}{x_{1}+1}-\frac{x_{2}}{x_{2}+1}=\frac{x_{1}\left(x_{2}+1\right)-x_{2}\left(x_{1}+1\right)}{\left(x_{1}+1\right)\left(x_{2}+1\right)}$
Donc: $T\left(x_{1} ; x_{2}\right)=\frac{x_{1}-x_{2}}{\left(x_{1}+1\right)\left(x_{2}+1\right)} \times \frac{1}{x_{1}-x_{2}}=\frac{1}{\left(x_{1}+1\right)\left(x_{2}+1\right)}$
$3)$$ a)$ Sur $I=]-\infty ;-1[$ :
Soit $\left.x_{1} \in\right]-\infty ;-1\left[\right.$ et $\left.x_{2} \in\right]-\infty ;-1\left[\quad x_{1} \neq x_{2}\right.$
Donc $x_{1} \prec-1$ et $x_{2} \prec-1$
Donc $x_{1}+1 \prec 0$ et $x_{2}+1 \prec 0$
Donc $\left(x_{1}+1\right)\left(x_{2}+1\right) \succ 0$
Donc : $T\left(x_{1} ; x_{2}\right)=\frac{1}{\left(x_{1}+1\right)\left(x_{2}+1\right)} \succ 0$ sur $\left.I=\right]-\infty ;-1[$
D’où : g que est strictement croissante sur $I=]-\infty ;-1[$
$b)$ Sur $J=]-1 ;+\infty[$ :
Soit $\left.x_{1} \in\right]-1 ;+\infty\left[\right.$ et $\left.x_{2} \in\right]-1 ;+\infty\left[\quad x_{1} \neq x_{2}\right.$
Donc $x_{1} \succ-1$ et $x_{2} \succ-1$
Donc $\quad x_{1}+1 \succ 0$ et $x_{2}+1 \succ 0$
Donc $\left(x_{1}+1\right)\left(x_{2}+1\right) \succ 0$
Donc $T\left(x_{1} ; x_{2}\right)=\frac{1}{\left(x_{1}+1\right)\left(x_{2}+1\right)} \succ 0$ sur $\left.J=\right]-1 ;+\infty[$
D’où: g que est strictement croissante sur $J=]-1 ;+\infty[$
$4)$ Tableau de variation :
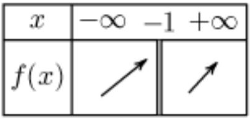
Exercice 20:
Soit $f$ une fonction tel que : $f(x)=x+\frac{1}{x}$
$1)$ Déterminer $D_{f}$ et étudier la parité de $f$
$2) $ Calculer Le taux d’accroissement $T\left(x_{1} ; x_{2}\right)$ de $f$ entre $x_{1}$ et $x_{2}$ deux éléments de $D_{f}$ tel que : $x_{1} \neq x_{2}$
$3)$ Étudier les variations de $f$ sur $I=] 0 ; 1]$ puis sur $J=[1 ;+\infty[$
$4)$ En déduire les variations de $f$ sur $D_{f}$
$5)$ Dresser le tableau de variations de $f$ sur $D_{f}$
$1)$ On a $f(x) \in \mathbb{R}$ équivaut à: $x \neq 0$
Donc $D_{f}=\mathbb{R}-\{0\}=\mathbb{R}^{*}$
Pour tout réel $x$ si $x \in \mathbb{R}^{*}$, alors $-x \in \mathbb{R}^{*}$
$f(-x)=-x+\frac{1}{-x}=-x-\frac{1}{x}=-\left(x+\frac{1}{x}\right)$
$f(-x)=-f(x)$
Donc $f$ est une fonction impaire.
$2)$ $f\left(x_{1}\right)-f\left(x_{2}\right)=\left(x_{1}+\frac{1}{x_{1}}\right)-\left(x_{2}+\frac{1}{x_{2}}\right)=x_{1}+\frac{1}{x_{1}}-x_{2}-\frac{1}{x_{2}}$
$=\frac{x_{1}^{2} \times x_{2}+x_{2}-x_{2}^{2} \times x_{1}-x_{1}}{x_{1} \times x_{2}}$
$=\frac{x_{1} \times x_{2}\left(x_{1}-x_{2}\right)+x_{2}-x_{1}}{x_{1} \times x_{2}}=\frac{\left(x_{1}-x_{2}\right)\left(x_{1} \times x_{2}-1\right)}{x_{1} \times x_{2}}$
$T\left(x_{1} ; x_{2}\right)=\frac{\left(x_{1}-x_{2}\right)\left(x_{1} \times x_{2}-1\right)}{x_{1} \times x_{2}} \times \frac{1}{x_{1}-x_{2}}=\frac{x_{1} \times x_{2}-1}{x_{1} \times x_{2}}$
$a)$ Sur $I=] 0 ; 1]: \quad$ Soient $\left.\left.x_{1} \in\right] 0 ; 1\right]$ et $\left.\left.x_{2} \in\right] 0 ; 1\right]$
Donc $0 \prec x_{1} \leq 1$ et $0 \prec x_{2} \leq 1 \quad x_{2}+1 \prec 0$
Donc $0 \prec x_{1} x_{2} \leq 1$ et $x_{1} \neq x_{2}$
Donc $\quad x_{1} x_{2}-1 \prec 0$ et on a : $0 \prec x_{1} x_{2}$
Donc $T\left(x_{1} ; x_{2}\right)=\frac{x_{1} \times x_{2}-1}{x_{1} \times x_{2}} \prec 0$
D’où : f est strictement décroissante sur $I=] 0 ; 1]$
b) Sur $J=[1 ;+\infty[$ :
Soient $x_{1} \in\left[1 ;+\infty\left[\right.\right.$ et $x_{2} \in[1 ;+\infty[$.
Donc $x_{1} \geq 1$ et $x_{2} \geq 1$
Donc $\quad x_{1} x_{2} \geq 1$ et $x_{1} \neq x_{2}$
Donc $\quad x_{1} x_{2} \succ 1$ par suite : $x_{1} x_{2}-1 \succ 0$
Et on a $0 \prec x_{1} x_{2}$ Donc $T\left(x_{1} ; x_{2}\right)=\frac{x_{1} \times x_{2}-1}{x_{1} \times x_{2}} \succ 0$
D’où : f est strictement croissante sur $J=[1 ;+\infty[$
$3)$ f est impaire et le symétrique de $I=] 0 ; 1$ ] est
l’intervalle $I^{\prime}=[-1 ; 0[$ et le symétrique de $J=\left[1 ;+\infty\left[\right.\right.$ est l’intervalle $\left.\left.J^{\prime}=\right]-\infty ;-1\right]$
Puisque : f est strictement décroissante sur $I$ alors f est strictement décroissante sur $I^{\prime}$
Puisque : f est strictement croissante sur $J$ alors f est strictement croissante sur $J^{\prime}$
$5)$ par suite le tableau de variations de f sur $D_{f}$ est :
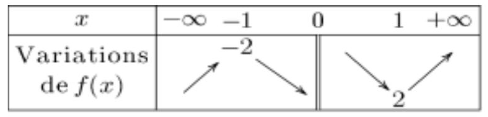
$f(1)=1+\frac{1}{1}=2$ et $f(-1)=-1-\frac{1}{1}=-2$
Exercice 21:
Soit $f$ une fonction numérique tel que : $f(x)=5 x^{2}+3$.
• Montrer que $f(0)=3$ est un minimum de $f$ sur $\mathbb{R}$
$D_{f}=\mathbb{R}$; On a pour tout $x \in \mathbb{R}$
$x^{2} \geq 0$ donc $5 x^{2} \geq 0$ car $5 \succ 0$
Par suite $5 x^{2}+3 \geq 3$ et on a $f(0)=3$
Donc pour tout $x \in \mathbb{R} \quad f(x) \geq f(0)$
D’où : $f(0)=3$ est un minimum de f sur $\mathbb{R}$
Exercice 22:
Soit g une fonction numérique tel que : $g(x)=-4 x^{2}+1$
Montrer que: $g(0)=1$ est un maximum de $g$ sur $\mathbb{R}$
Soit $g$ une fonction numérique tel que : $g(x)=-4 x^{2}+1 \quad D_{g}=\mathbb{R}$
On a pour tout $x \in \mathbb{R} \quad x^{2} \geq 0$ donc $-4 x^{2} \leq 0$ car $-4 \prec 0$
Par suite $-4 x^{2}+1 \leq 1$ et on a $g(0)=1$
Donc pour tout $x \in \mathbb{R} \quad g(x) \leq g(0)$
D’où : $g(0)=1$ est un maximum de g sur $\mathbb{R}$
Exercice 23:
Soit f une fonction numérique tel que : $f(x)=-4 x^{2}+4 x+5$
$1)$$a)$ Montrer que $f(x)=6-(2 x-1)^{2}$pour tout $x \in \mathbb{R}$
$b)$ Montrer que $f(x) \leq 6$ pour tout $x \in \mathbb{R}$
$2)$ Calculer : $f\left(\frac{1}{2}\right)$ et en déduire les extrémums de f sur $\mathbb{R}$
$1) $$a)$ On a $D_{f}=\mathbb{R}$
$6-(2 x-1)^{2}=6-\left(4 x^{2}-4 x+1\right)=6-4 x^{2}+4 x-1=-4 x^{2}+4 x+5$
Donc : $f(x)=6-(2 x-1)^{2}$
$b)$ Pour tout $x \in \mathbb{R} \quad$ on a : $(2 x-1)^{2} \geq 0$
Par suite $-(2 x-1)^{2} \leq 0$ donc $6-(2 x-1)^{2} \leq 6$
C’est-à-dire : pour tout $x \in \mathbb{R}: f(x) \leq 6$
$2)$ On a $f\left(\frac{1}{2}\right)=6-\left(2 \times \frac{1}{2}-1\right)^{2}=6-(1-1)^{2}=6$
On a pour tous $x \in \mathbb{R}: 6-(2 x-1)^{2} \leq 6$
Alors : $f(x) \leq f\left(\frac{1}{2}\right)$ pour tout $x \in \mathbb{R}$
Donc: $f\left(\frac{1}{2}\right)=6$ est un maximum de f sur $\mathbb{R}$
Exercice 24:
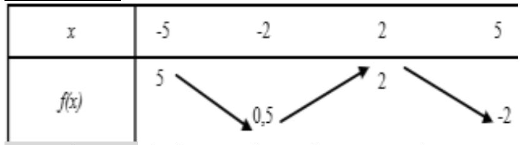
Du tableau de variation ,déduire les extrémums de f
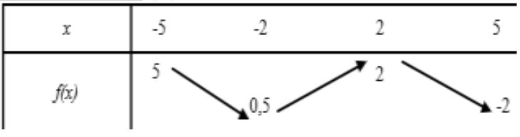
Du tableau de variation on a :Le nombre $2$ est une valeur maximale de $ f$ au point $x_{0}=2$
Le nombre $0.5$ est une valeur Minimale de $f$ au point $x_{0}=-2$
Exercice 25:
Donner le tableau de variations et représenter la courbe des fonctions numériques définies par :
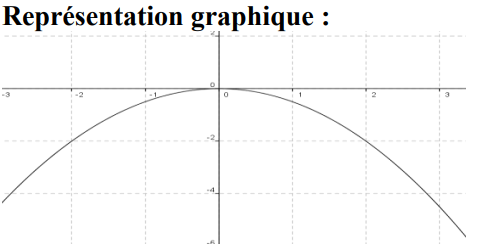
$1)$ $f(x)=\frac{1}{2} x^{2} \quad$
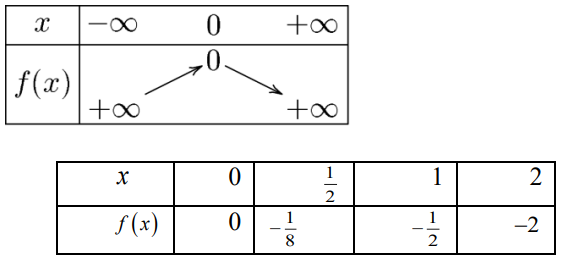
$2)$ $f(x)=-\frac{1}{2} x^{2}$
$1)$ $D_{f}=\mathbb{R}$ et On a $a=\frac{1}{2} \succ 0$
Tableau de variations de $ f$
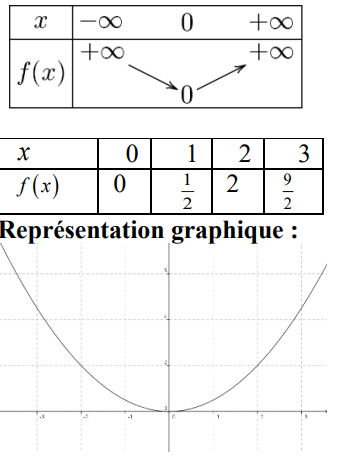
$2)$ Soit $f$ une fonction numérique tel que :
$f(x)=-\frac{1}{2} x^{2} \quad \text { et } \quad D_{f}=\mathbb{R} $
On a : $a=-\frac{1}{2} \prec 0$
Tableau de variations de $f$ :
Exercice 26:
Soit f une fonction numérique tel que: $f(x)=2 x^{2}-4 x-2$ ,$\left(C_{f}\right)$ Sa courbe représentative
$1)$ Déterminer $D_{f}$ et déterminer $\alpha$ et $\beta$ tel que : $f(x)=2(x-\alpha)^{2}+\beta$ pour tout $x \in \mathbb{R}$
$2)$ Déterminer le Tableau de variations de $f$
$3)$ Tracer la courbe représentative $\left(C_{f}\right)$ dans le repère $(O ; \vec{i} ; \vec{j})$
$1)$ On a : $f$ est une fonction polynôme; donc: $D_{f}=\mathbb{R} \quad$
On a $: a=2$ et $b=-4$ et $c=-2$ $\left(f(x)=a x^{2}+b x+c\right)$
Donc $\alpha=-\frac{b}{2 a}=\frac{4}{2 \times 2}=1$ et $\beta=-\frac{\Delta}{4 a}=-\frac{32}{4 \times 2}=-4$
Pour tout réel $x \in \mathbb{R}$ on peut écrire sous la forme : $f(x)=a\left(x+\frac{b}{2 a}\right)^{2}-\frac{\Delta}{4 a}=2(x-1)^{2}-4$
$(f(1)=2-4-2=-4)$
$2)$ Soit $W(1 ;-4)$ Donc dans le repère $(0 ; \vec{i} ; \vec{j})$ la courbe $\left(C_{f}\right)$ c’est une parabole de sommet $W(1 ;-4)$ et d’axe de symétrie la droite $x=1$
Tableau de variations de $f$ : On a $a=2 \succ 0$ donc :
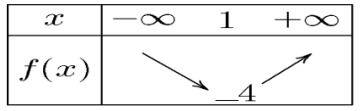
$3)$
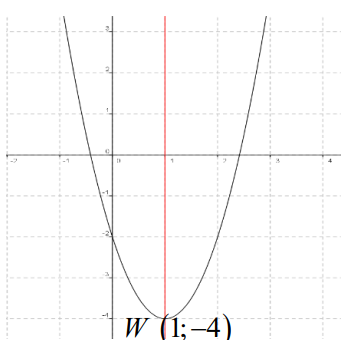
Exercice 27:
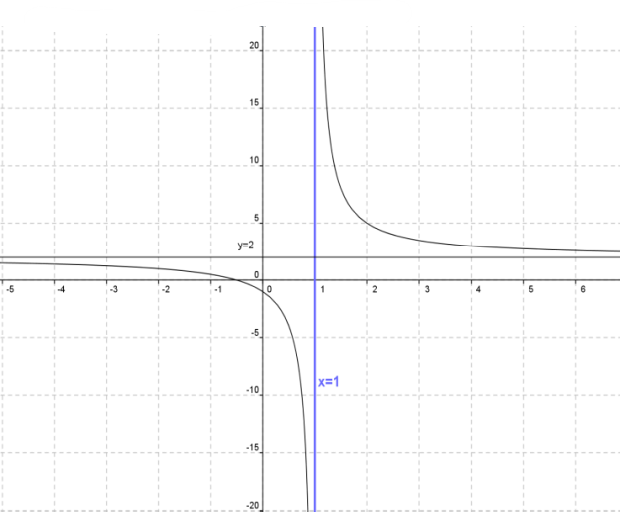
Soit f une fonction numérique tel que : $f(x)=\frac{2 x+1}{x-1}$, $\left(C_{f}\right)$ Sa courbe représentative
$1)$ Déterminer $D_{f}$ et déterminer $\alpha$ et $\beta$ et $k$ tel que : $f(x)=\beta+\frac{k}{x-\alpha}$ pour tout $x \in \mathbb{R}$
$2)$ Déterminer le Tableau de variations de $f$
$3)$ Tracer la courbe représentative $\left(C_{f}\right)$ dans le repère $(O ; \vec{i} ; \vec{j})$
$1)$ On a $f(x) \in \mathbb{R}$ signifie que : $x-1 \neq 0$ équivaut à : $x \neq 1 \quad$
Donc $D_{f}=\mathbb{R}-\{1\}$
Si $x \in \mathbb{R}-\{1\}$ on a: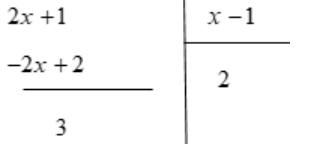
Alors : $f(x)=\frac{2 x+1}{x-1}=\frac{2(x-1)+3}{x-1}=\frac{2(x-1)}{x-1}+\frac{3}{x-1}=2+\frac{3}{x-1}$
$2)$ $f(x)-2=\frac{3}{x-1}$ signifie $y-2=\frac{3}{x-1}$
On pose $\left\{\begin{array}{l}x-1=X \\ y-2=Y\end{array}\right.$
Donc $\left\{\begin{array}{l}x=X+1 \\ y=Y+2\end{array}\right.$
$y=\frac{2 x+1}{x-1}$ ssi $Y=\frac{3}{X}$
$\underline{\text { Tableau de variations de }} X \longrightarrow \frac{3}{X}(3 \succ 0)$
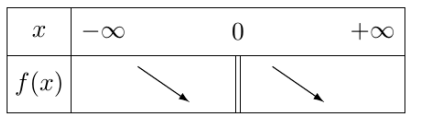
On a $\left\{\begin{array}{l}X=0 \\ Y=0\end{array}\right.$ donc $\left\{\begin{array}{l}x=1 \\ y=2\end{array}\right.$
Donc le tableau de variations de $x \longrightarrow \frac{2 x+1}{x-1}$
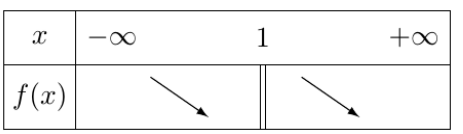
$4)$ Représentation graphique
Exercice 28:
Soit f une fonction numérique tel que : $f(x)=\frac{-2 x+1}{2 x-4}$, $\left(C_{f}\right)$ Sa courbe représentative
$1) $ Déterminer $D_{f}$
$2)$ Déterminer $\alpha$ et $\beta$ et $k \mathrm{tel}$ que : $f(x)=\beta+\frac{k}{x-\alpha} \quad$ pour tout $x \in \mathbb{R}$
$3)$ Déterminer le Tableau de variations de $f$
$4)$ Tracer la courbe représentative $\left(C_{f}\right)$ dans le repère ( $O ; i ; j$ )
$1)$Soit f une fonction numérique tq : $f(x)=\frac{-2 x+1}{2 x-4}$
On a $f(x) \in \mathbb{R}$ signifie que : $2 x-4 \neq 0$
C’est-à-dire : $x \neq 2$ Donc $D_{f}=\mathbb{R}-\{2\}$
$2)$ Si $x \in \mathbb{R}-\{2\}$ on a:
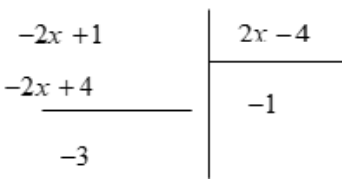
$f(x)=\frac{-(2 x-4)-3}{2 x-4}=\frac{-(2 x-4)}{2 x-4}+\frac{-3}{2 x-4}=-1+\frac{-3 / 2}{x-2}$
$3)$ $f(x)+1=\frac{-3 / 2}{x-2}$
On pose $\alpha=2$ et $\beta=-1$ et soit $W(2 ;-1)$
– Donc dans le repère $(W ; \vec{i} ; \vec{j})$ l’équation de $\left(C_{f}\right)$ est $Y=\frac{-3 / 2}{X}$ avec $Y=y+1$ et $X=x-2$
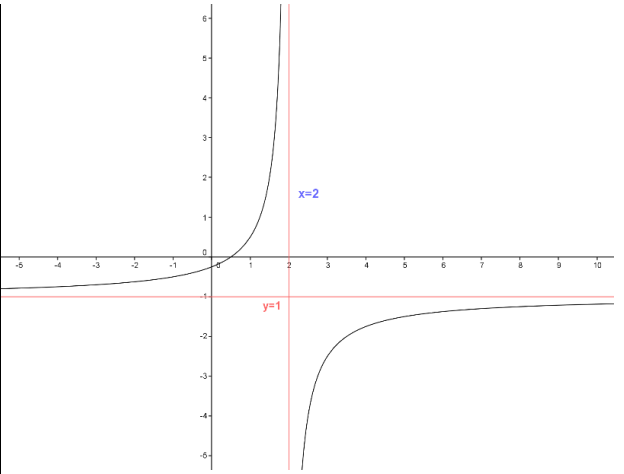
Donc / $\left(C_{f}\right)$ est une hyperbole de centre $W$ et d’asymptotes les droites d’équations respectives $x=2 \text { et } y=-1$
– Tableau de variations $X \longrightarrow \frac{-3 / 2}{X}(-3 / 2 \prec 0)$
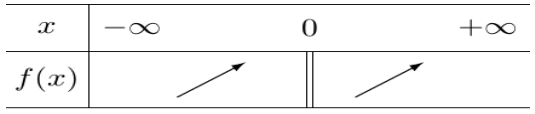
– Donc le tableau de variations de : $x \longrightarrow \frac{-2 x+1}{2 x-4}$
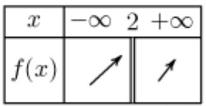
$4)$

Exercice 29:
On considère la fonction $f$ définie par: $f(x)=x^{2}-2 x$
$1)$ Etudier la parité de $f$
$2)$$ a) $Ecrire le plus simplement possible $T=\frac{f(a)-f(b)}{a-b}$ pour tout a et $b$ distincts de $D_{f}$
$b)$ Déduire les variations de $f$ sur chacun des deux intervalles $]-\infty ; 1]$ et $[1 ;+\infty[$
$c)$ Dresser le tableau des variations de $f$ sur $D_{f}$
$d)$ Déduire les extremums de $f$ (s’ils existent)
$3)$ Calculer $f(2)$ et $f(3)$ puis tracer $C_{f}$ dans un repère orthonormé.
$4$ On considère la fonction $g$ définie par $g(x)=x|x|-2 x$
$a) $Etudier la parité de $g$
$b)$ Montrer que $g(x)=f(x)$ pour tout $x$ de $[0 ;+\infty[$
$c)$Dresser le tableau des variations de $g$ (justifier)
$d)$ Tracer $C_{g}$ dans le même repère (avec une autre couleur)
$1)$ On a $D_{f}=\mathbb{R}$
$f(1)=-1$ et $f(-1)=3$ donc $f(-1) \neq f(1)$ et $f(-1) \neq-f(1)$ d’où $f$ est ni paire ni impaire
$2)$ $a)$ Pour tout a et $b$ distincts de $D_{f}$ on $a$
$T=\frac{f(a)-f(b)}{a-b}=\frac{a^{2}-2 a-b^{2}+2 b}{a-b}=\frac{(a-b)(a+b)-2(a-b)}{a-b}=a+b-2$
$b)$ Sur l’intervalles ]- $\infty$;1] on a a $\leq 1$ et $\mathrm{b} \leq 1$ donc $\mathrm{a}+\mathrm{b} \leq 2 \mathrm{c}$ – $\mathrm{a}-\mathrm{d} \mathrm{a}+\mathrm{b}-2 \leq 0$ donc fest décroissante sur ] $-\infty$;1]
Sur l’intervalle $[1 ;+\infty[$ on $a \quad a \geq 1$ et $b \geq 1$ donc $a+b \geq 2$ c-à-d $a+b-2 \geq 0$ donc $f$ est croissante sur $[1 ;+\infty[$
$c)$ Le tableau des variations de $f$ sur $D_{f}$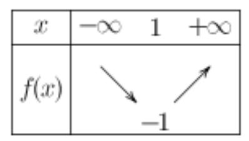
$d)$ -1 est la valeur minimale de $f$ sur $D_{f}=\mathbb{R}$
$3)$ On a $f(2)=0$ et $f(3)=3 \quad C_{f}$ est une parabole de sommet $\Omega(1 ;-1)$
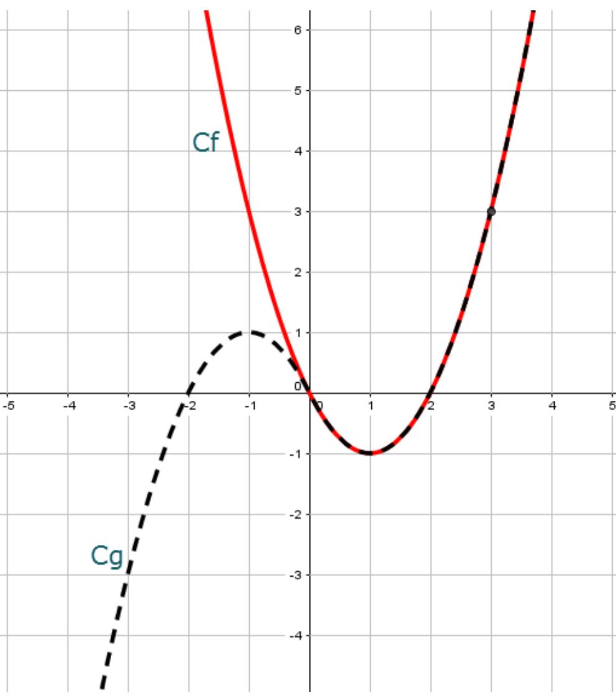
$4)$On considère la fonction $g$ définie par $g(x)=x|x|-2 x$
$a)$ On a $D_{g}=\mathbb{R}$ et $g(-x)=-x|-x|+2 x=-x|x|+2 x=-(x|x|-2 x)=-g(x) \quad$ car $|-x|=|x|$ donc $g$ est impaire
$b)$ Pour tout $x$ de $[0 ;+\infty[$ on a $|-x|=|x|$ donc $g(x)=f(x)$
$c)$ $f$ et $g$ ont les même variations sur $[0 ;+\infty[$
g est impaire et décroissante sur $[0 ; 1]$ donc décroissante sur $[-1 ; 0]$
$g$ est impaire et croissante sur $[1 ;+\infty[$ donc croissante sur $]-\infty ;-1]$
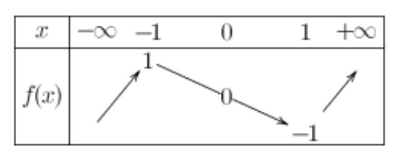
$d)$ La courbe $C_{g}$ (voir la figure ci-dessus )
Exercice 30:
Soient $f$ et $g$ deux fonctions définies par : $f(x)=x^{2}-2 x$ et $g(x)=\frac{x}{x-2}$
$1)$ Déterminer $D_{g}$ et vérifier que pour tout $x$ de $D_{g}: g(x)=1+\frac{2}{x-2}$
$2)$ Donner les tableaux de variations de $f$ et $g$
$3)$ Déterminer les points d’intersection de $\left(C_{f}\right)$ et $\left(C_{g}\right)$ avec les axes du repère
$4)$ Tracer les courbes $\left(C_{f}\right)$ et $\left(C_{g}\right)$ dans le même repère orthonormé $(O, \vec{i}, \vec{j})$
$5)$ Déterminer algébriquement les points d’intersection de $\left(C_{f}\right)$ et $\left(C_{g}\right)$
$6)$ Résoudre graphiquement l’inéquation $f(x) \leq g(x)$
$7)$ Soit $h$ la fonction définie par : $h(x)=\frac{|x|}{|x|-2}$
$a)$ Déterminer $D_{h}$
$b)$ Montrer que la fonction $h$ est paire
$1)$ $\left.\triangleright D_{g}=\{x \in \mathbb{R} / x-2 \neq 0\}=\{x \in \mathbb{R} / x \neq 2\}=\right]-\infty, 2[\cup] 2,+\infty[$
$\triangleright$ Soit $x \in D_{g}$,on a: $1+\frac{2}{x-2}=\frac{x-2+2}{x-2}=\frac{x}{x-2}=g(x)$
Donc pour tout $x$ de $D_{g}: g(x)=1+\frac{2}{x-2}$
$2)$ $\triangleright f(x)=x^{2}-2 x$
On a : $a=1$ donc $a>0$
Et on a $: \frac{-b}{2 a}=\frac{-(-2)}{2(1)}=1$ et $f\left(\frac{-b}{2 a}\right)=f(1)=-1$

$\triangleright g(x)=\frac{x}{x-2}$
On a : $\left|\begin{array}{cc}1 & 0 \\ 1 & -2\end{array}\right|=-2$ donc $\left|\begin{array}{cc}1 & 0 \\ 1 & -2\end{array}\right|<0$
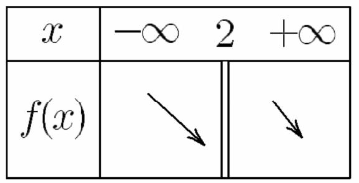
$3)$ $\triangleright$ Déterminons les points d’intersection de $\left(C_{f}\right)$ avec l’axe des abscisses :
Résolvons dans $\mathbb{R}$ l’équation : $f(x)=0$
$f(x)=0$ équivaut à $x^{2}-2 x=0$
$f(x)=0 \text { équivaut à } x=0 \text { ou } \quad x=2$
Et par suite : $\left(C_{f}\right) \cap(O x)=\{A(1,0) ; B(2,0)\}$
$\triangleright$ Déterminons les points d’intersection de $\left(C_{f}\right)$ avec l’axe des ordonnées :
Calculons $f(0)$ :
On a: $f(0)=0$
Donc $\left(C_{f}\right) \cap(O y)=\{O(0,0)\}$
$\triangleright$ Déterminons les points d’intersection de $\left(C_{g}\right)$ avec l’axe des abscisses :
Résolvons dans $\mathbb{R}-\{2\}$ l’équation : $g(x)=0$
$g(x)=0$ équivaut à $\frac{x}{x-2}=0$
$g(x)=0$ équivaut à $x=0$
Et par suite : $\left(C_{g}\right) \cap(O x)=\{O(0,0)\}$
$\triangleright$ Déterminons les points d’intersection de $\left(C_{g}\right)$ avec l’axe des ordonnées :
Calculons $g(0)$ :
On a: $g(0)=0$
Donc $\left(C_{g}\right) \cap(O y)=\{O(0,0)\}$
$4)$
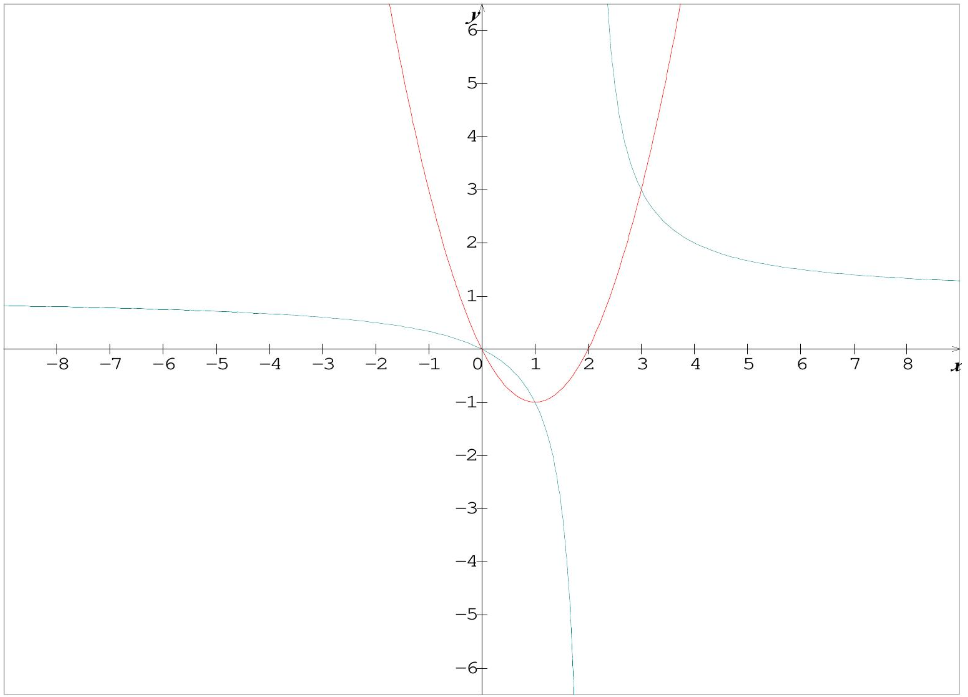
$5)$ Résolvons dans $\mathbb{R}-\{1\}$ l’équation : $f(x)=g(x)$
$f(x)=g(x)$ équivaut à $x^{2}-2 x=\frac{x}{x-2}$
équivaut à $x(x-2)-\frac{x}{x-2}=0$
équivaut à $x\left[(x-2)-\frac{1}{x-2}\right]=0$
équivaut à $x\left[\frac{(x-1)(x-3)}{x-2}\right]=0$
équivaut à $x=0$ ou $x=1$ ou $x=3$
Et par suite $\left(C_{f}\right) \cap\left(C_{g}\right)=\{A(1,-1) ; O(0,0) ; \mathrm{D}(3,3)\}$
$6)$ graphiquement l’inéquation $f(x) \leq g(x)$ équivaut à déterminer les intervalles dont on a $\left(C_{f}\right)$ est au-dessous de $\left(C_{g}\right)$
c-à-d $S=[0,1] \cup] 2,3]$
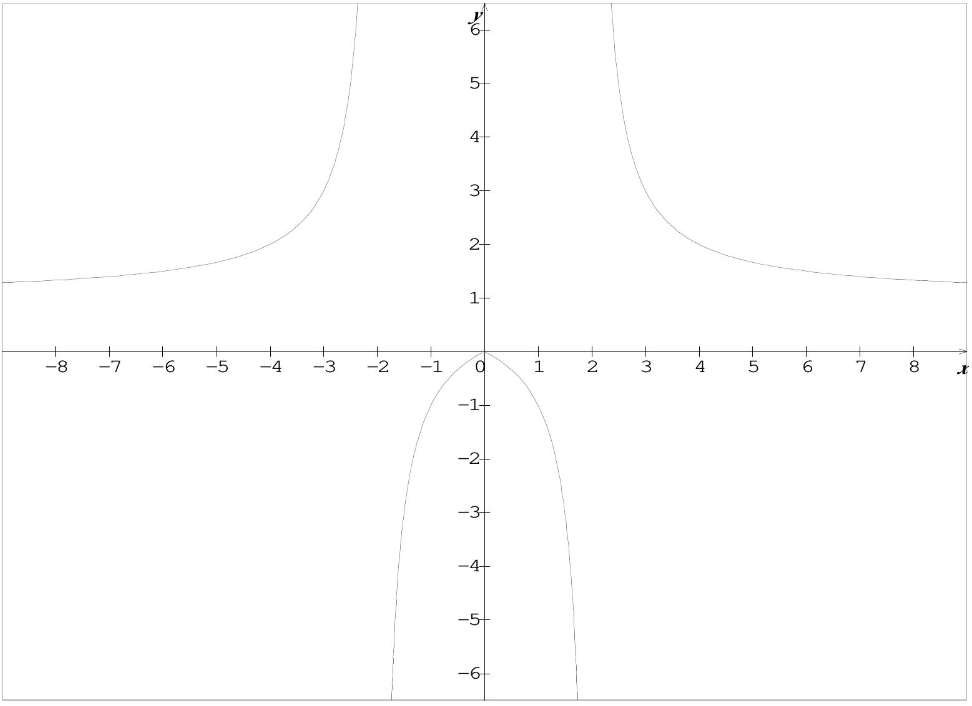
$7)$ $h(x)=\frac{|x|}{|x|-2}$
$a)$ $\left.D_{h}=\{x \in \mathbb{R} /|x|-2 \neq 0\}=\{x \in \mathbb{R} /|x| \neq 2\}=\mathbb{R}-\{-2,2\}=\right]-\infty,-2[\cup]-2,2[\cup] 2,+\infty[$
$b)$ Soit $x \in D_{h}$, on a :
$\triangleright-x \in D_{h} \quad\left(\right.$ car $D_{h}$ est symétrique par rapport à 0$)$
$\triangleright h(-x)=\frac{|-x|}{|-x|-2}=\frac{|x|}{|x|-2}=h(x)$
Donc pour tout $x$ de $D_{h}$, on a : $\left\{\begin{array}{c}-x \in D_{h} \\ h(-x)=h(x)\end{array}\right.$
D’où la fonction $h$ est paire
$c)$ Soit $x \in \mathbb{R}^{+}-\{2\}$, on a :
$h(x)=\frac{|x|}{|x|-2}=\frac{x}{x-2}=g(x) $
$ \text { car }\left\{\begin{array}{l}
x \geq 0 \\
|x|=x
\end{array}\right.$
Donc $h(x)=g(x)$ pour tout $x$ de $\mathbb{R}^{+}-\{2\}$
$d)$
Généralités sur les fonctions exercices corrigés
Généralités sur les fonctions exercices corrigés
Généralités sur les fonctions exercices corrigés