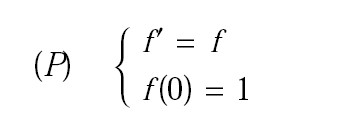Introduction à la fonction exponentielle
1 Introduction
De nombreux phénomènes physiques, biologiques, économiques ou autres sont modélisés
par une fonction f qui est proportionnelle à sa dérivée f ′.
Par exemple, le phénomène de désintégration des noyaux radioactifs, l’activité de désintégration
à l’instant t est proportionnelle au nombre de noyaux à l’instant t : N′(t) = kN(t)
Nous allons ici nous intéresser à l’une des fonctions de ce type.
Plus particulièrement, que peut-on dire d’une fonction qui serait égale à sa dérivée ?
Nous connaissons déjà au moins une fonction égale à sa dérivée : la fonction nulle ! Mais
cette fonction est sans intérêt. Notre objectif est d’en rechercher d’autres.
2 Théorie : de l’importance de la condition initiale
Supposons qu’il existe une fonction f , non nulle, définie et dérivable sur R telle que : f ′= f sur R
1) Soit λ ∈ R. On pose g = λ f .
Démontrer que : g′ = g sur R.
2) Soit g une fonction vérifiant aussi g′ = g sur R.
Que peut-on dire de : f + g ?
3) Supposons maintenant qu’il existe une fonction f , définie et dérivable sur R, vérifiant les conditions :
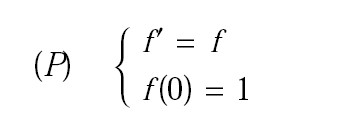
a) On considère la fonction φ définie sur R par : φ(x) = f (x) f (−x)
ROC • Montrer que φ est une fonction constante égale a 1 sur R.
• En déduire que f ne s’annule pas sur R puis que la fonction f est strictement positive.
b) Démontrer que si g est une fonction qui vérifie (P) alors g = f sur R.
ROC – On pourra considérer la fonction h définie sur R par h = f ⁄g .
Dans la suite, la fonction f est l’unique fonction satisfaisant les conditions : (l’unicité vient d’être montrée, l’existence sera montrée plus tard)