ℵ La proportionnalité -Cours
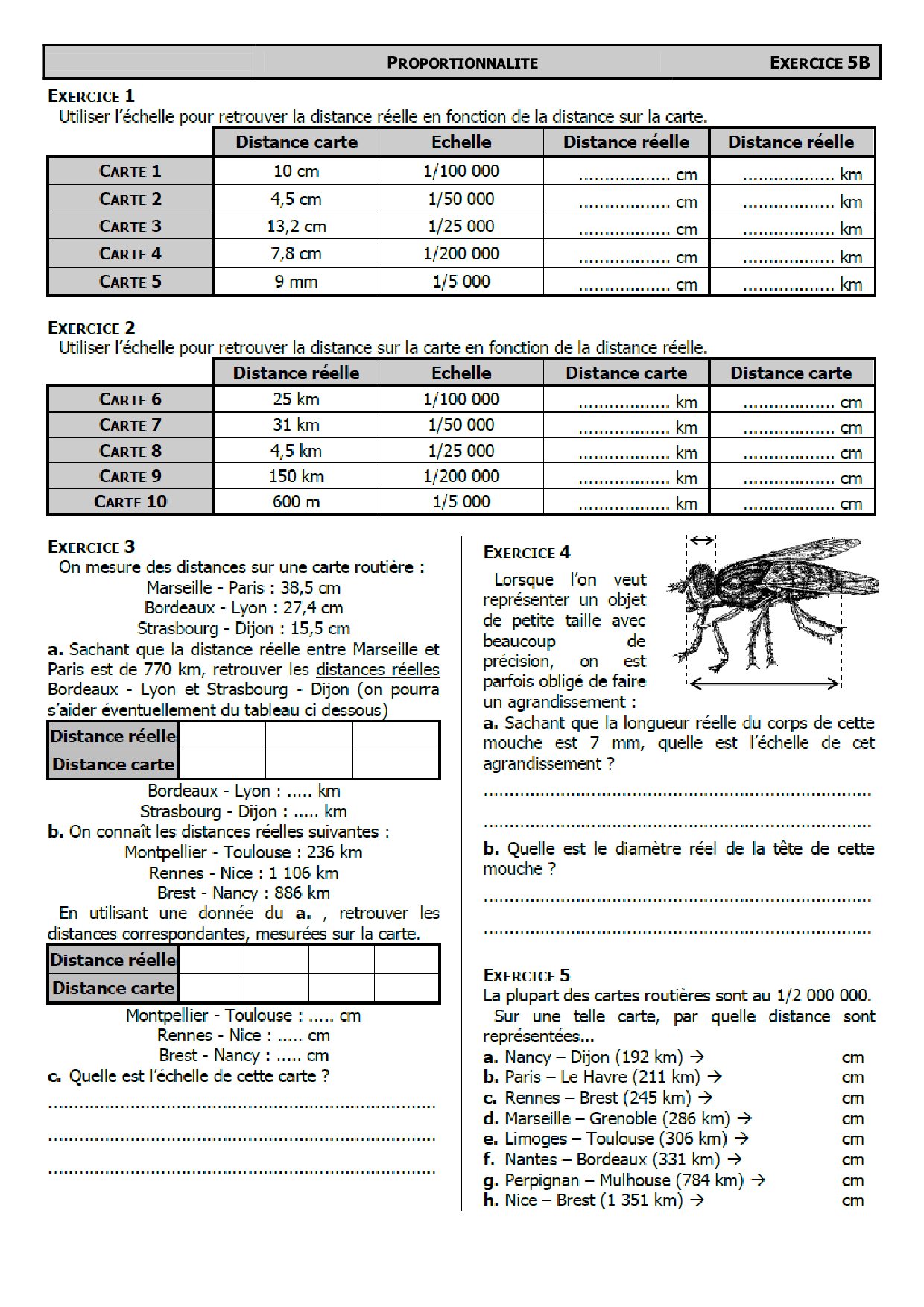
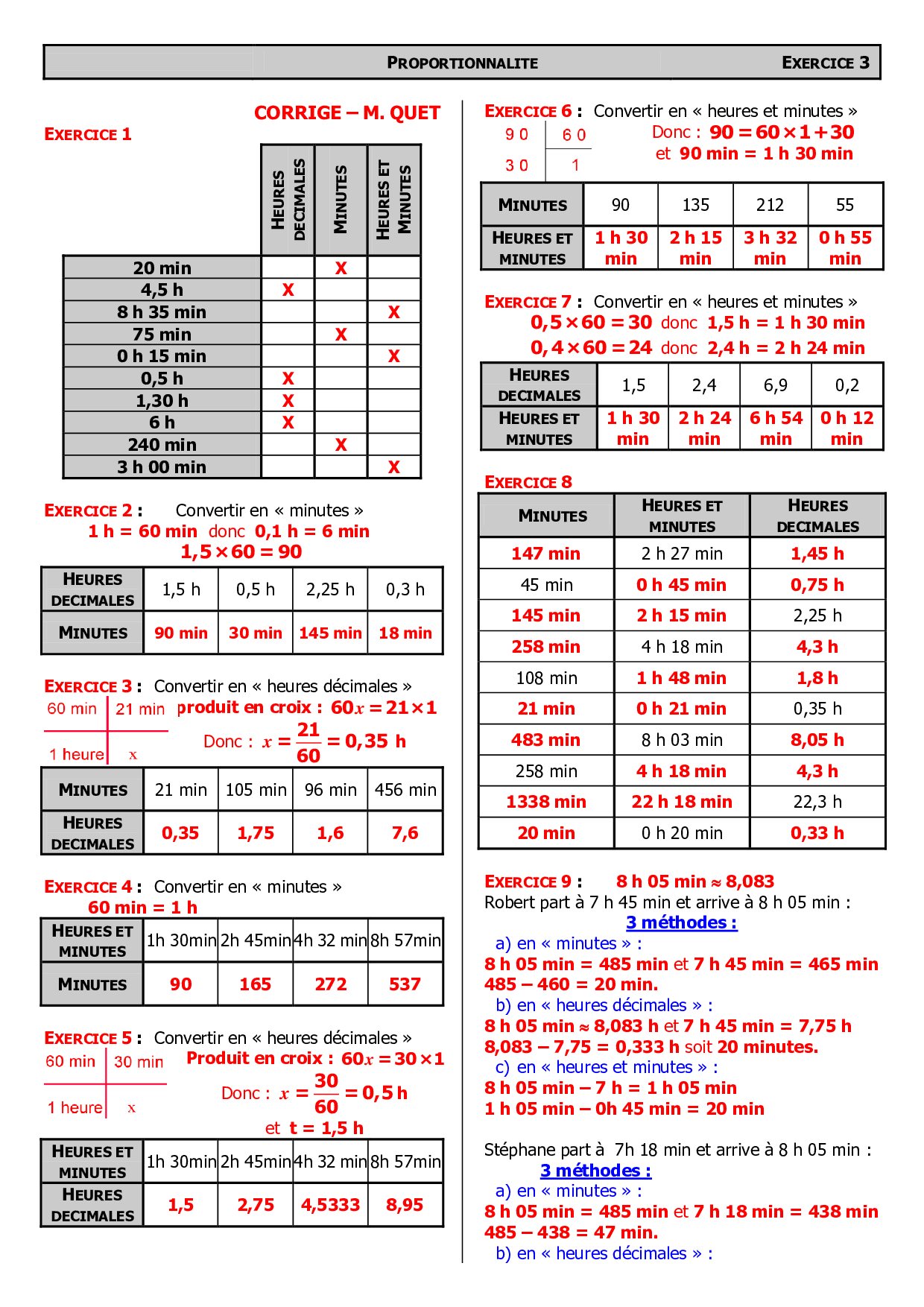
ℵ La proportionnalité -Exercice1
ℵ La proportionnalité -Exercice2
ℵ La proportionnalité -Exercice3
ℵ La proportionnalité -Exercice4
ℵ La proportionnalité -Exercice5
1 Proportionnalité
Vous allez trouver ci-dessous un exemple de proportionnalité:
1.1 Exemple

Pour trouver le périmètre d’un carré, on multiplie toujours la longueur du côté par le même nombre : quatre.
P = 4 × C. Ici on a exprimé le périmètre en fonction de la longueur du côté.
Le périmètre et la longueur du côté sont proportionnels.
Le tableau est appelé : tableau de proportionnalité.
4 et 1/4 sont les coefficients de proportionnalité.
2 Reconnaître un tableau de proportionnalité
Propriété :
Un tableau de deux lignes est un tableau de proportionnalité si pour passer d’un nombre de la première ligne au nombre de la seconde ligne situé dans la même colonne on multiplie toujours par le même nombre.
Exemple1 :

Ce tableau est un tableau de proportionnalité car on multiplie les nombres de la première ligne par 3 pour trouver les nombres de la seconde ligne. Un des coefficients de proportionnalité est 3.
15 × 3 = 45 ; 10 ×3 = 30 ;0,8 × 3 = 2,4 , 5 ×3 = 15
Remarque 1 : 10 + 5 = 15 et 30 + 15 = 45
2 ×5 = 10 et 2 × 15 = 30


3 Compléter un tableau de proportionnalité
Voici un tableau de proportionnalité à compléter.

a) Trouver un des coefficients de proportionnalité :
Il suffit de connaître les nombres d’une colonne.
Soit k le coefficient de proportionnalité qui permet de passer de la première ligne à la seconde ligne.
On sait grâce à la première colonne que : 15 × k = 37,5 c’est une équation.
Vérifions : 15 × 2,5 = 37,5 OK
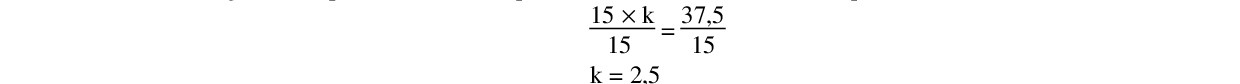
b) Maintenant que l’on connaît le coefficient on peut calculer les nombres de la seconde ligne grâce à ceux de la première ligne.
10 × 2,5 = 25 , 25 × 2,5 = 62,5 , 42 × 2,5 = 105 , 30 × 2,5 = 75 ,0,175 × 2,5 =0,4375
Remarque :
on pouvait calculer certaines valeurs sans le coefficient
car 15 × 2 = 30 donc pour la cinquième colonne on trouve 37,5 × 2 = 75
car 15 + 10 = 25 donc grâce aux deux premières colonnes on trouve la troisième : 37,5 + 25 = 62,5
c) Pour trouver les nombres de la première ligne à partir de ceux de la seconde ligne on peut :
soit diviser la seconde ligne par le coefficient déjà trouver : 24 :2,5 = 9,6
soit chercher le coefficient de proportionnalité qui permet de passer de la seconde ligne à la première :