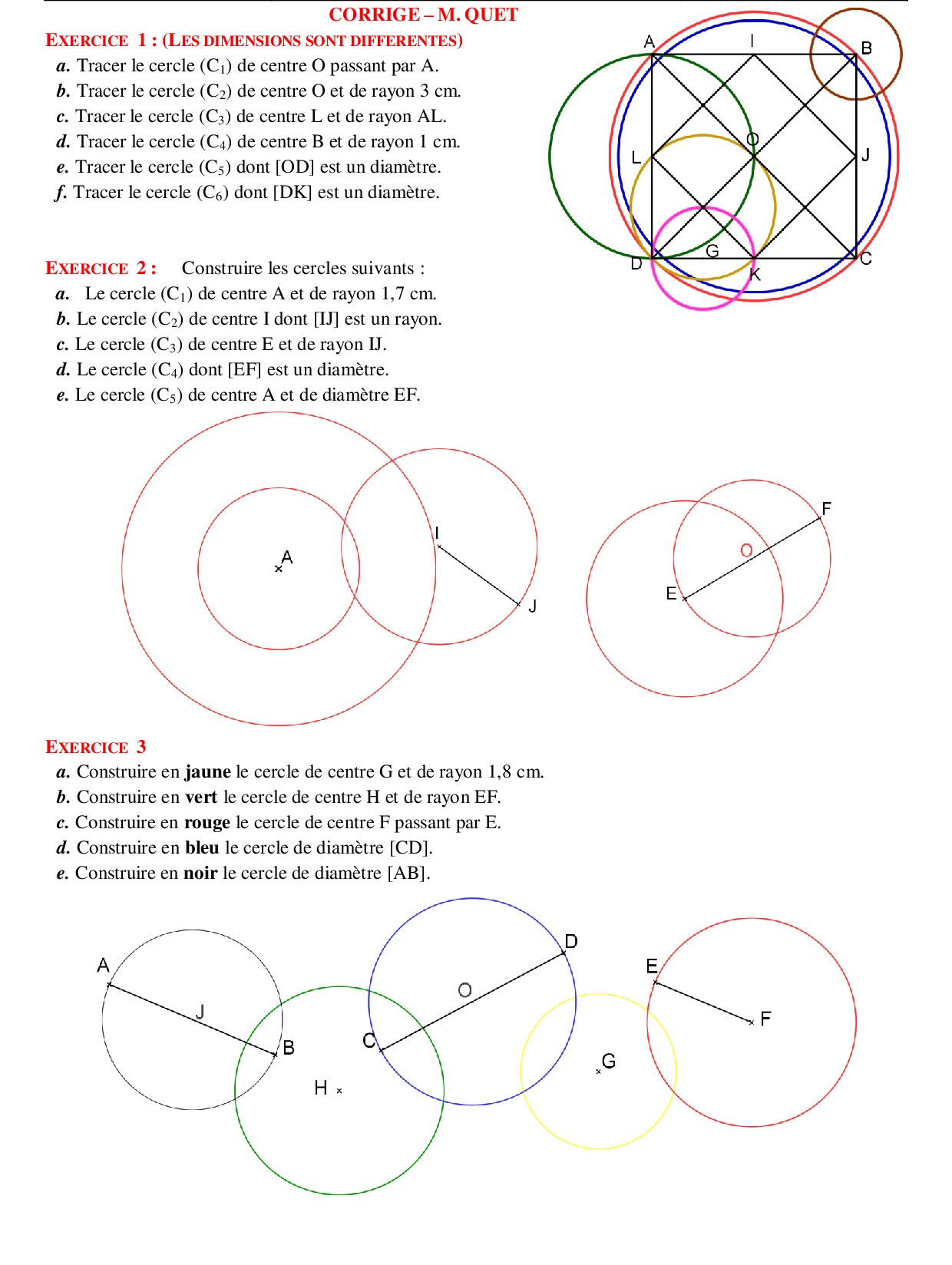
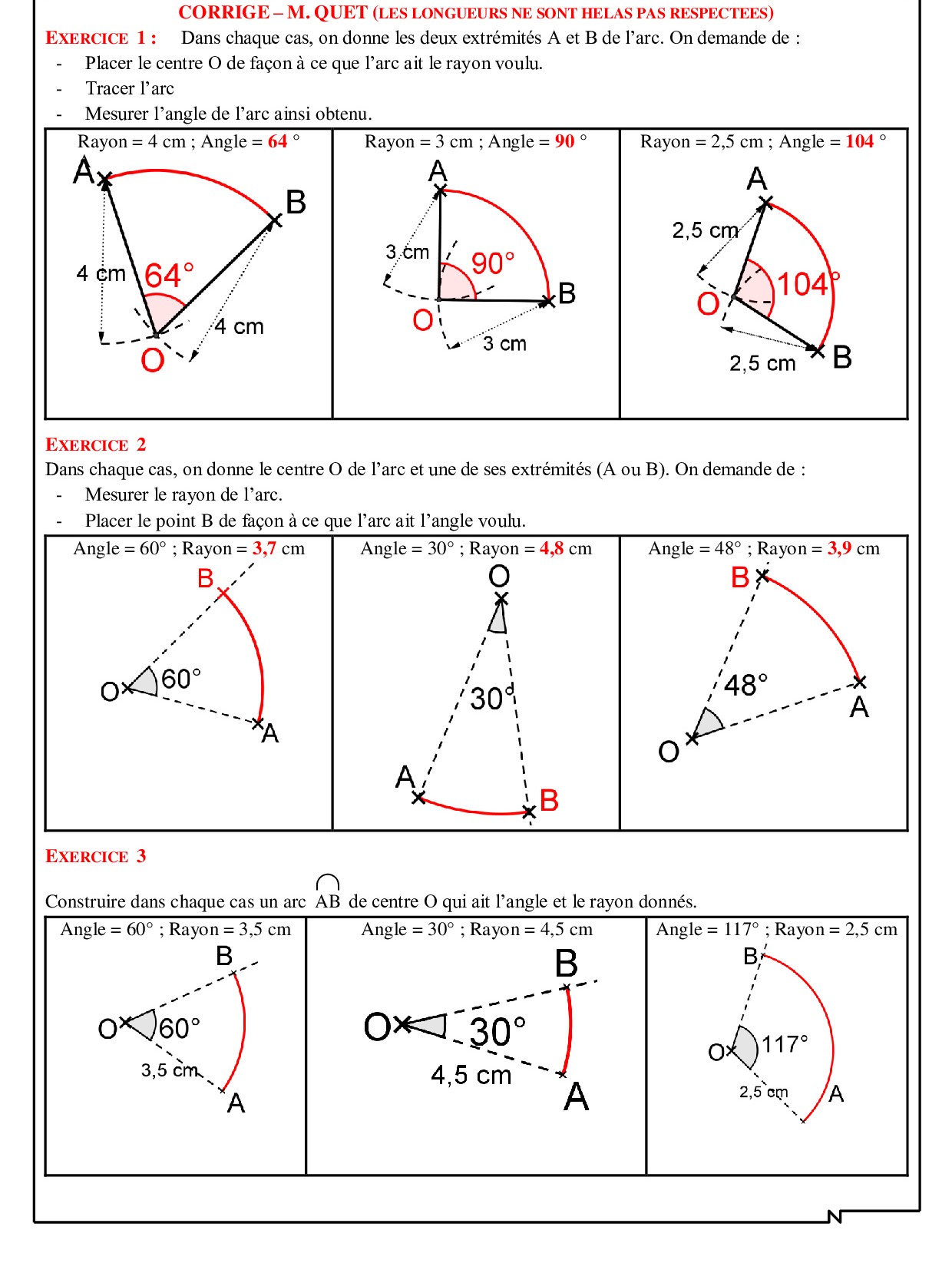
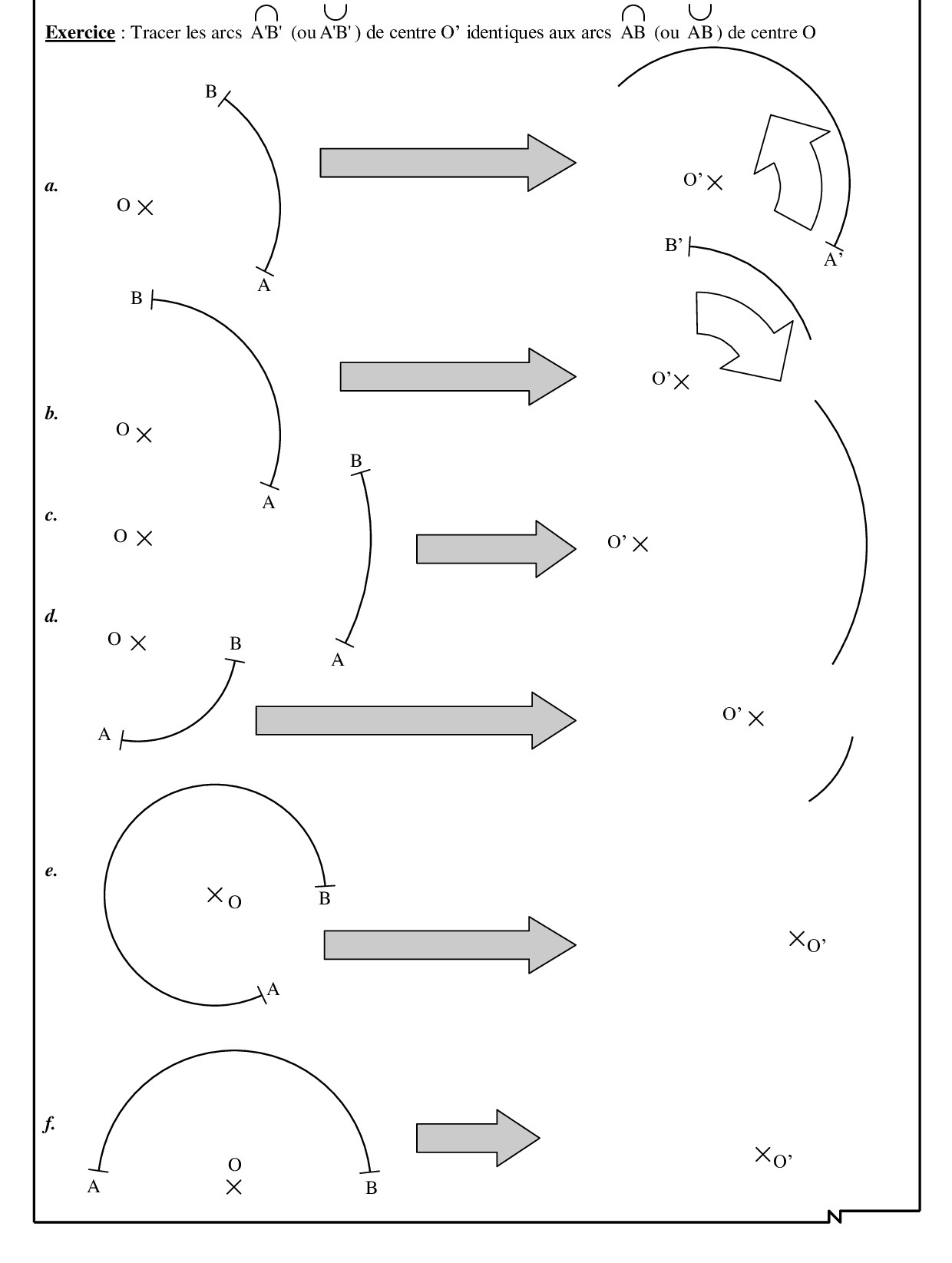
1− Généralités
On va commencer par définir le cercle:
Définition
⋄ Un cercle, en général noté (C ) ou juste C , de centre O, est formé de tous les points qui se trouvent à la même distance du point O. Cette distance qui ne change pas porte alors un nom : c’est le rayon.
⋄ Un arc de cercle est une portion de cercle limitée par deux points appelés extrémités.
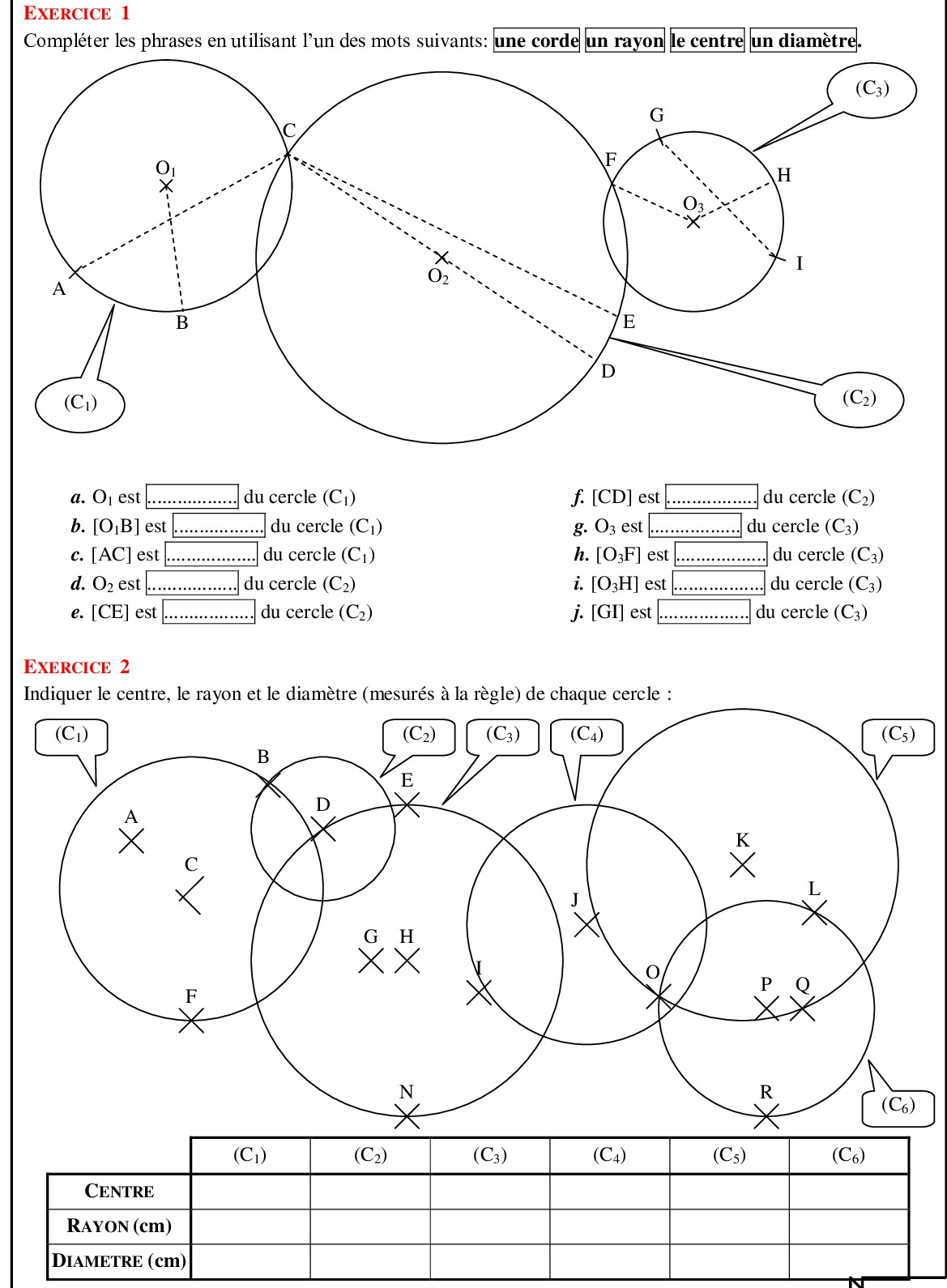
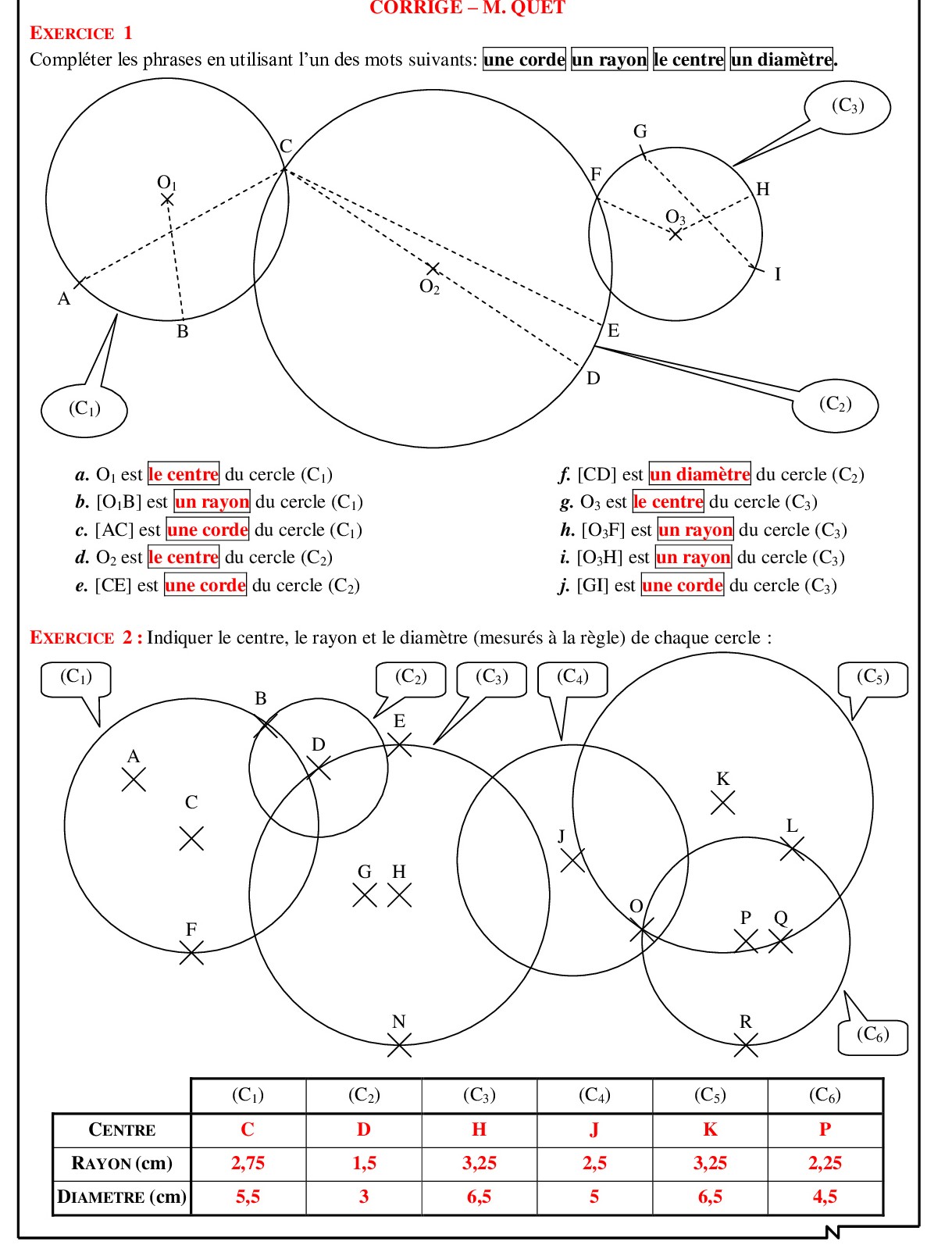
⋄ Une corde est un segment dont les extrémités sont deux points du cercle.
⋄ Un diamètre est une corde qui passe par le centre du cercle.
2-Vocabulaire et propriétés
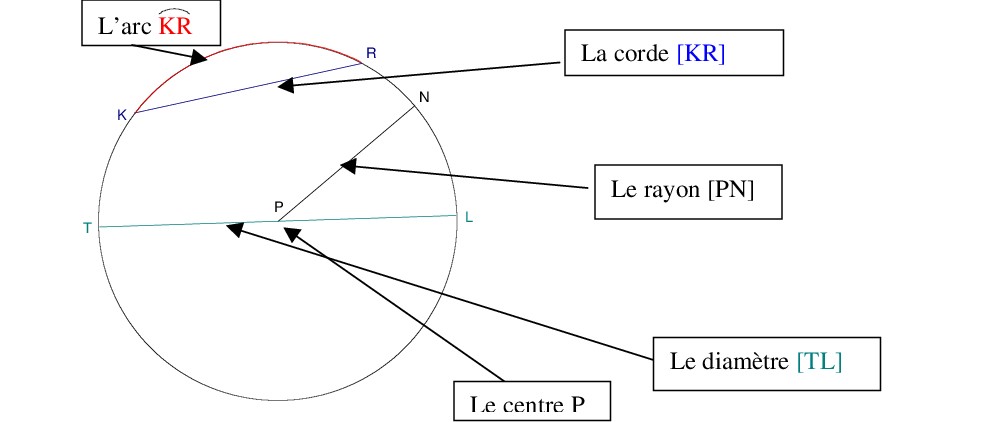
Le cercle C de centre P et de rayon 6 cm est l’ensemble de tous les points N tels que NP= 6cm.
Propriété 1 :
Si N Î C alors NP = 6 cm
Propriété 2(réciproque de la 1) :
Si NP = 6 cm N Î C
Le disque de rayon 6 cm, de centre P est l’ensemble des points N tels que PN £ 6 cm.

Définition
Le périmètre d’un cercle, noté P, est la mesure de son contour, et uniquement de son contour.
Attention:
ans tout problème, qu’il soit de proportionnalité ou non, il faut faire extrêmement attention aux unités qui doivent être les mêmes du début à la fin !
— Certaines figures seront dessinées avec une longueur donnée à l’intérieur : il ne faudra surtout pas l’additionner aux autres pour le calcul du périmètre ! !
3− Constructions de triangles
Pour construire un triangle ABC tel que AB = 3 cm, AC = 5 cm et BC = 6 cm,
1. on représente le côté le plus long horizontalement (moins de risque que la figure ne déborde de la feuille), ici BC = 6 cm ;
2. on ouvre le compas de 3 cm, on pique sur B et on trace un arc de cercle ;
3. on ouvre le compas de 5 cm, on pique sur C et on trace un autre arc de cercle ;
4. les deux arcs de cercle doivent se couper en un point : c’est le point A recherché. Si les deux arcs ne se coupent pas, il faut les prolonger en répétant les étapes 2 et 3.