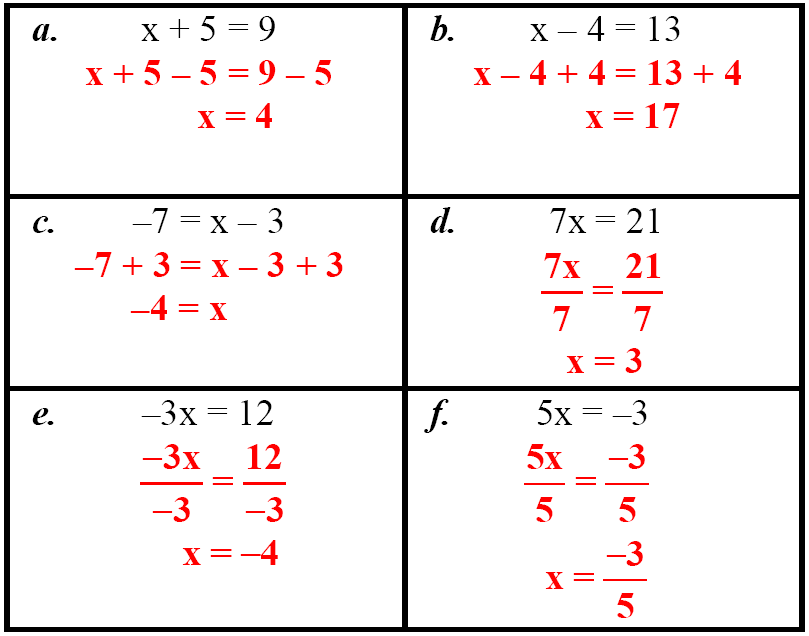Cours et exercices corrigés classe 3ème: Cliquez ici
ℵ Les équations _Cours
ℵ Les équations _Exercice1
ℵ Les équations _Exercice2
ℵ Les équations _Exercice3
ℵ Les équations _Exercice4
ℵ Les équations _Exercice5
ℵ Les équations _Exercice6
Les équations sont, en mathématiques, des relations (en général des égalités) contenant une ou plusieurs variables.
1 Généralité
Définition :
Une équation est une égalité dans laquelle un ou plusieurs nombres sont inconnus. Ce(s) nombre(s) est (sont) appelé(s) inconnue(s) et remplacé(s) par une(des) lettre(s).
L’expression à gauche (à droite) du signe = est le membre gauche (droit).
Exemples :
4x + 2 = 10
3y = 4x – 2
(x + 7) (x – 5) = 0
Solution :
Un nombre est solution de 4x + 2 = 10 si lorsque qu’on teste (voir fiche 2, §2-2), les deux membres de l’équation sont égaux.
¨ Parmi ces nombres y a-t-il des solutions de l’équation précédente : 5 ; 2 ; 1 ?
4 × 5 + 2 = 22 donc 5 n’est pas une solution.
4 × 2 + 2 = 10 donc 2 est une solution
4 × 1 + 2 = 6 donc 1 n’est pas une solution
¨ Parmi ces nombres, 2 ;4, y a-t-il des solutions de : 3x + 1 = 4x – 3 ?
3 × 2 + 1 = 7 et 4 × 2 – 3 = 5
Les deux membres de l’équation ne sont pas égaux donc 2 n’est pas une solution.
3 × 4 + 1 = 13 et 4 × 4 – 3 = 13
Les deux membres de l’équation sont égaux donc 4 est une solution
¨ Parmi ces nombres, 8 ; 5 ;-7 y a-t-il des solutions de (x + 7) (x – 5) = 0 ?
(8 + 7) ( 8 – 5) = 15 ´ 3 = 45 donc 8 n’est pas une solution.
(5 + 7) ( 5 – 5) = 13 ´ 0 = 0 donc 5 est une solution
(-7 + 7) (7 – 5) = 0 ´ 2 = 0 donc –7 est aussi une solution
¨ Cas où il y a plusieurs inconnues différentes :
x = 2 et y = 5 sont-elles solutions de 3y = 4x – 2 ?
3× 5 = 15 et 4 × 2 – 2 =6 donc elles ne sont pas solutions. Et x = 5 et y = 6 ?
3 × 6 = 18 et 4 × 5 – 2 = 18 donc ce sont bien des solutions.
Définition :
résoudre une équation c’est trouver toutes les solutions de cette équation.
2 Résolution des équations x + a = b et ax = b
Règles
On peut ajouter, soustraire le même nombre dans les deux membres d’une équation sans en changer les solutions.
On peut multiplier, diviser, par le même nombre les deux membres d’une équation sans en changer les solutions.
Exemples :
x + 45 = 458 , 7 + x = 23 ,x – 5 = 12
x + 45 – 45 = 458 – 45 , 7 + x – 7= 23 – 7 , x – 5 + 5 = 12 +5
x = 413 ,7 + x + (-7) = 23 –7 ,x + (-5) + 5 = 12 + 5
,x = 16 , x = 17
Pour être sûr de ses calculs il faut vérifier en testant la valeur trouvée.
413 + 45 = 458 OK 7 + 16 = 23 OK 17 – 5 = 12 OK
Résoudre ces équations :

Résoudre ces équations :

Résoudre ces équations :

Résoudre ces équations :
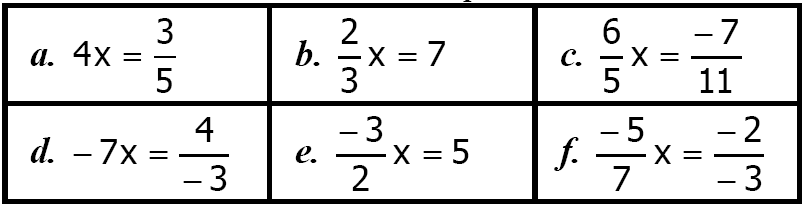
Résoudre ces équations :

Traduire chaque phrase par une équation, puis
trouver le nombre x :
a. « Le double de x vaut 6 ».
b. « Le triple de x vaut 33 ».
c. « 9 retranché de x vaut 4 » .
d. « Le double de x ajouté à 6 vaut 0 ».
e. « 6 retranché du triple de x vaut 9 ».
f. « Le quintuple de x ajouté à 2 vaut x ».
g. « Le double de la somme de x et de 3 vaut x ».
h. « La somme de x et de 6 vaut le triple de la somme de x et de 1 ».
Traduire chaque phrase par une équation, puis
trouver le nombre x :
« Le double de x vaut 6 ». → 2x = 6
« Le triple de x vaut 33 ». → 3x = 33
« 9 retranché de x vaut 4 » . → x – 9 = 4
« Le double de x ajouté à 6 vaut 0 » : 2x + 6 = 0
« 6 retranché du triple de x vaut 9 » : 3x – 6 = 9
« Le quintuple de x ajouté à 2 vaut x » 5x + 2 = x
« Le double de la somme de x et de 3 vaut x » : 2(x + 3) = x
« La somme de x et de 6 vaut le triple de la somme
de x et de 1 » : x +6 = 3(x +1)
1- Résoudre les équations suivantes :
3 – 2x – 3 – x = 5 – x + 18
7 + 5x = 7x – 13
2x = 13 – 4x
2- Résoudre les équations suivantes :
3 (x + 1) – (x – 9) + (x + 3) = (x + 4) + (x + 2) – (11 – x)
6(x – 3) -3(x – 2) = 4(3 – x) + 5
4(x – 4) + 25(x + 1) = 10(2x + 3) + 15
7(2x – 5) – 5(3x + 1) = 6(x – 4) – 7
(x – 1)(x + 3) = (x + 4)(x – 2)
(x + 3)(x + 5) = (x + 1)(x + 9)
3(x – 3) = (x – 4)(x + 1) – (x – 5)(x – 1)
1- Résoudre les équations suivantes :

2- Résoudre les équations suivantes :