les polynômes – Exercices corrigés
Exercice 1:
Déterminer parmi les expressions suivantes ceux qui sont des polynômes et déterminer si c’est possible leurs degrés : $a \in \mathbb{R}$
$P(x)=\frac{1}{4} x^{3}+\frac{\sqrt{2}}{2} x^{2}-\sqrt{3}$
$ Q(x)=2 x^{2}-x-\sqrt{x}$
$R(x)=5\left|x^{2}\right|+4|x|-5$
$M(x)=\frac{5}{3} x^{2}+x+2-7 x^{4}$
$N(x)=x^{2}+\frac{1}{x}+3 \quad $
$ O(x)=4 $
$ E(x)=(a-1) x^{4}+x^{2}+x+1$
$P(x)$ est un polynôme et $d^{\circ} P=3$
$Q(x)$ et $R(x)$ et $N(x)$ ne sont pas des polynômes
$M(x)$ est un polynôme et $d^{\circ} M=4$
$O(x)$ est un polynôme et $d^{\circ} O=0$
$E(x)$ est un polynôme :
• Si $a-1 \neq 0$ c.à.d $a \neq 1$ alors $d^{\circ} E=4$
• Si $a-1 \neq 0$ c.à.d $a=1$ alors $d^{\circ} E=2$
Exercice 2:
Déterminer un polynôme P de degré 2 tel que : $P(0)=P(1)=5$ et $P(-2)=3$
P de degré 2 donc P s’écrit sous la forme :
$P(x)=a x^{2}+b x+c$
On a $P(0)=5$ , alors $a \times 0^{2}+b \times 0+c=5$ donc $c=5$
On a $P(1)=5$ , alors $a \times 1^{2}+b \times 1+c=5$ donc $a+b+c=5$ donc $a+b+5=5$
donc $a+b=0$ (1)
On a $P(-2)=3$ , alors $a \times(-2)^{2}+b \times(-2)+5=3$
donc $4 a-2 b+5=3$
donc $4 a-2 b=-2$ (2)
d’où : On a le système suivant: $\left\{\begin{array}{l}4 a-2 b=-2 \\ a+b=0\end{array}\right.$
Donc $\left\{\begin{array}{l}4 a-2 b=-2 \\ b=-a\end{array}\right.$
Alors $4 a+2 a=-2$ donc $6 a=-2$
donc $a=-\frac{1}{3}$
Et $b=\frac{1}{3}$
Alors : $\quad P(x)=-\frac{1}{3} x^{2}+\frac{1}{3} x+5$
Exercice 3:
Lesquels des polynômes ci-dessous sont égaux ? Expliquez
$P(x)=2 x^{3}-2 x^{2}+x-3$
$Q(x)=2 x^{2}(x-2)+(x-1)(2 x+3) \quad$
$R(x)=2 x^{3}+3 x^{2}-2 x-3$
$Q(x)=2 x^{2}(x-2)+(x-1)(2 x+3)=2 x^{3}-4 x^{2}+2 x^{2}+3 x-2 x-3$
$Q(x)=2 x^{3}-2 x^{2}+x-3 \quad \operatorname{deg}(\mathrm{Q})=3$
$P(x)=2 x^{3}-2 x^{2}+x-3 \quad \operatorname{deg}(\mathrm{P})=3$
Donc : $P(x)=Q(x)$ car $\operatorname{deg}(\mathrm{P})=\operatorname{deg}(\mathrm{Q})$ et les coefficients de leurs monômes de même degré sont égaux.
Mais $P(x) \neq R(x)$ car les coefficients de leurs monômes de même degré ne sont pas égaux
Exercice 4:
Soit : $P(x)=x^{4}-2 x^{3}+x^{2}-1$ et $Q(x)=a x^{5}+(b+c) x^{4}+(c+d) x^{3}+d x^{2}+e$
Déterminer $a , b , c$ et $d$ pour que: $P=Q$
$P=Q$ c.à.d $P(x)=Q(x)$ donc On a le système suivant :
$\left\{\begin{array}{l} a = 0 \\ b + c = 1 \\ c + d = – 2 \\ d = 1 \\c = – 1\end{array}\right.$
Alors $\left\{\begin{array}{l} a=0 ; d=1 ; c=-1 \\ c=-2-d=-2-1=-3 \\ b=1-c=1+3=4\end{array}\right.$
Donc $Q(x)=x^{4}-2 x^{3}+x^{2}-1$
Exercice 5:
Soit les polynômes suivants :
$P(x)=12 x^{4}-36 x^{3}+47 x^{2}-30 x+7$
$Q(x)=\left(2 x^{2}-3 x+1\right)\left(a x^{2}+b x+c\right)$
Déterminer $a , b , c$ pour que: $P=Q$
$P=Q$ ssi $P(x)=Q(x)$ pout tout $x$
$Q(x)=\left(2 x^{2}-3 x+1\right)\left(a x^{2}+b x+c\right)$
$=2 a x^{4}+2 b x^{3}+2 c x^{2}-3 a x^{3}-3 b x^{2}-3 c x+a x^{2}+b x+c$
$Q(x)=2 a x^{4}+(2 b-3 a) x^{3}+(2 c-3 b+a) x^{2}+(b-3 c) x+c$
Donc: $\left\{\begin{array}{l}2 a=12 \\ 2 b-3 a=-36 \\ a-3 b+2 c=47 \\ b-3 c=-30 \\ c=7\end{array}\right.$
Donc : $\left\{\begin{array}{l}a=0 \\ b=-9 \\ c=7\end{array}\right.$
On vérifie que : $a-3 b+2 c=47$ est vraie
Donc: $Q(x)=\left(2 x^{2}-3 x+1\right)\left(6 x^{2}-9 x+7\right)$
Exercice 6:
Etudier l’égalité des polynômes dans les cas suivants :
1) $P(x)=x^{3}+2 x^{2}(x-1)+x\quad$ et $\quad Q(x)=x^{2}(3 x-2)+x$
2) $P(x)=(x-1)^{3} \quad$ et $\quad Q(x)=x^{3}-3 x^{2}-3 x+1$
1) $P(x)=x^{3}+2 x^{2}(x-1)+x=x^{3}+2 x^{3}-2 x^{2}+x=3 x^{3}-2 x^{2}+x$
$Q(x)=x^{2}(3 x-2)+x=3 x^{3}-2 x^{2}+x=P(x)$
2) $P(x)=(x-1)^{3} =x^{3}-3 x^{2}+3 x-1$
Donc: $Q(x) \neq P(x)$ car $\quad(3 \neq-3)$
Exercice 7:
I- Soient $P(x)$ et $Q(x)$ deux polynômes
• Calculer dans chacun des cas suivants :
$P(x)+Q(x) \quad ; \quad P(x)-Q(x) \quad; \quad 3 P(x)-2 Q(x)$
1) $P(x)=x^{3}+2 x^{2}-1 \quad ; \quad Q(x)=3 x^{4}-x^{3}+x$
2) $P(x)=x^{5}-x^{2}+3 \quad ; \quad Q(x)=-x^{5}+x^{2}-5$
II- Calculer $P(x) \times Q(x)$ et $(P(x))^{2}$ dans chacun des cas
suivants et comparer : $\operatorname{deg}(\mathrm{PQ})$ et $deg (P) +deg (Q)$
1) $P(x)=x^{2}-1 \quad ; \quad Q(x)=x^{2}+2 x-3$
2) $P(x)=x^{4}-x^{2}+2 \quad ; \quad Q(x)=3 x+2$
I)
1) $P(x)=x^{3}+2 x^{2}-1 \quad $ ; $ \quad Q(x)=3 x^{4}-x^{3}+x$
On a: $P(x)+Q(x)=x^{3}+2 x^{2}-1+3 x^{4}-x^{3}+x$
donc $P(x)+Q(x)=3 x^{4}+2 x^{2}+x-1$
On a: $P(x)-Q(x)=x^{3}+2 x^{2}-1-3 x^{4}+x^{3}-x$
donc $P(x)-Q(x)=-3 x^{4}+2 x^{3}+2 x^{2}-x-1$
$On a : 3 P(x)-2 Q(x)=3\left(x^{3}+2 x^{2}-1\right)-2\left(3 x^{4}-x^{3}+x\right)$
$3 P(x)-2 Q(x)=3 x^{3}+6 x^{2}-3-6 x^{4}+2 x^{3}-2 x$
$3 P(x)-2 Q(x)=-6 x^{4}+5 x^{3}+6 x^{2}-2 x-3$
$\operatorname{deg}(P)=3 ; \operatorname{deg}(Q)=4 ; \operatorname{deg}(P+Q)=4 ;$ $\operatorname{deg}(P-Q)=4$
2) $P(x)=x^{5}-x^{2}+3 \quad ; \quad Q(x)=-x^{5}+x^{2}-5$
On a: $P(x)+Q(x)=x^{5}-x^{2}+3-x^{5}+x^{2}-5=-2$
On a: $P(x)-Q(x)=x^{5}-x^{2}+3+x^{5}-x^{2}+8=2 x^{5}-2 x^{2}+8$
On a: $3 P(x)-2 Q(x)=3\left(x^{5}-x^{2}+3\right)-2\left(-x^{5}+x^{2}-5\right)$
$3 P(x)-2 Q(x)=3 x^{5}-3 x^{2}+9+2 x^{5}-2 x^{2}+10$
$3 P(x)-2 Q(x)=5 x^{5}-5 x^{2}+19$
$\operatorname{deg}(P)=5 ; \operatorname{deg}(Q)=5 ; \operatorname{deg}(P+Q)=0 ;$ $\operatorname{deg}(P-Q)=5$
II)
1) on a $P(x)=x^{2}-1 \quad ; \quad Q(x)=x^{2}+2 x-3$
$P(x) \times Q(x)=\left(x^{2}-1\right)\left(x^{2}+2 x-3\right)=x^{5}+2 x^{4}-3 x^{3}-x^{2}-2 x+3$
$(P(x))^{2}=\left(x^{2}-1\right)^{2}=\left(x^{2}\right)^{2}-2 x^{2} \times 1+1=x^{4}-2 x^{2}+1$
2) $P(x)=x^{4}-x^{2}+2 \quad ; \quad Q(x)=3 x+2$
$P(x) \times Q(x)=(3 x+2)\left(x^{4}-x^{2}+2\right)=3 x^{5}+2 x^{4}-3 x^{3}-2 x^{2}+6 x+4$
$(P(x))^{2}=\left(x^{4}-x^{2}+2\right)^{2}=\left(x^{4}-x^{2}+2\right)\left(x^{4}-x^{2}+2\right)$
$(P(x))^{2}=\left(x^{4}-x^{2}+2\right)^{2}=x^{8}-2 x^{6}+5 x^{4}-4 x^{2}+4$
$\operatorname{deg}(P \times Q)=5 \quad \operatorname{deg}(P)=4 ; \operatorname{deg}(Q)=1$
Donc $\operatorname{deg}(P \times Q)=\operatorname{deg}(P)+\operatorname{deg}(Q)$ et $\operatorname{deg}\left(P^{2}\right)=2 \operatorname{deg}(P)$
Exercice 8:
Soit le polynôme : $P(x)=x^{3}-2 x^{2}-5 x+6$
Est-ce que les nombres suivants sont des racines du polynôme $P(x)$ (justifier) ? $1 ; 2 ; 3$; -2
$P(1)=1^{3}-2 \times 1^{2}-5 \times 1+6=1-2-5+6=0$
donc 1 est racine du polynôme $P(x)$
$P(2)=2^{3}-2 \times 2^{2}-5 \times 2+6=8-8-10+6=-4 \neq 0$
donc 2 n ‘est pas racine du polynôme $P(x)$
$P(3)=3^{3}-2 \times 3^{2}-5 \times 3+6=27-18-15+6=0$
donc 3 est racine du polynôme $P(x)$
$P(-2)=(-2)^{3}-2 \times(-2)^{2}-5 \times(-2)+6=-8-8+10+6=0$
donc -2 est racine du polynôme $P(x)$
Exercice 9:
Effectuer la division euclidienne de $P(x)=x^{3}+3 x^{2}-2 x-6$ par : $x+3$ et déterminer le quotient et le reste.
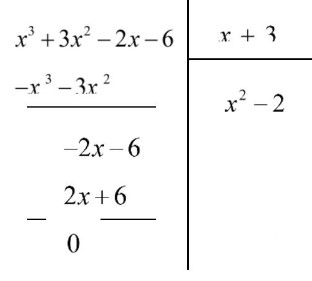
On a donc:
$P(x)=(x+3) Q(x)+P(-3)=(x+3)\left(x^{2}-2\right)+0=(x+3)\left(x^{2}-2\right)$
$Q(x)=x^{2}-2$ est le quotient et $P(-3)=0$ le reste.
Exercice 10:
Soit le polynôme : $P(x)=2 x^{2}-x-1$
1) Vérifier que 1 est racine du polynôme $P(x)$
2) Factoriser $P(x)$
1) $P(1)=2 \times 1^{2}-1-1=0$
Donc : 1 est racine du polynôme $P(x)$
2) 1 est racine du polynôme $P(x)$ donc: $P(x)$ est divisible par $x-1$
En effectuant la division euclidienne de $P(x)$ par $x-1$ On trouve : $Q(x)=2 x+1$
donc: $P(x)=(x-1)(2 x+1)$
Exercice 11:
Soit le polynôme : $P(x)=x^{3}+3 x^{2}-2 x-6$
1) calculer $P(-3)$ et que peut-on dire ?
2) déterminer le le polynôme $Q(x)$ tel que : $P(x)=(x+3) Q(x)$
1) En remplaçons x par -3 dans le polynôme $P(x)=x^{3}+3 x^{2}-2 x-6$
on a: $P(-3)=(-3)^{3}+3(-3)^{2}-2(-3)-6=-27+27+6-6=0$ donc -3 est racine du polynôme $P(x)$
2) $P(x)$ est divisible par $x+3$
Donc il existe un polynôme $Q(x)$ tel que :
$P(x)=(x+3) Q(x)$ et puisque le degré de $P(x)$ est 3 donc le degré de $Q(x)$ est 2 donc: $Q(x)=a x^{2}+b x+c(a \neq 0)$
Méthode 1: $P(x)=x^{3}+3 x^{2}-2 x-6$
$P(x)=(x+3)\left(a x^{2}+b x+c\right)$
Donc: $x^{3}+3 x^{2}-2 x-6=(x+3)\left(a x^{2}+b x+c\right)$
$=a x^{3}+(b+3 a) x^{2}+(c+3 b) x+3 c$
$=a x^{3}+b x^{2}+c x+3 a x^{2}+3 b x+3 c$
Donc : $a=1$ et $b+3 a=3$ et $3 c=-6$
Donc :et $b=0 a=1$ et $c=-2$
Donc: $Q(x)=x^{2}-2$
Méthode 2: $P(x)=x^{3}+3 x^{2}-2 x-6$.
$=x^{2}(x+3)-2(x+3)=(x+3)\left(x^{2}-2\right)$ donc: $Q(x)=x^{2}-2$
Méthode 3 : Effectuer la division euclidienne de $P(x)=x^{3}+3 x^{2}-2 x-6$ par $x+3$ et déterminer le quotient et le reste
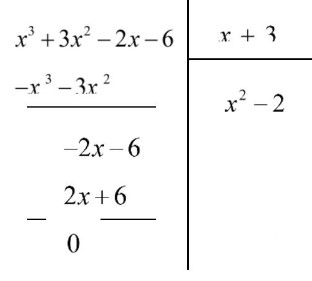
$P(x)=(x+3) Q(x)+P(-3)=(x+3)\left(x^{2}-2\right)+0=(x+3)\left(x^{2}-2\right)$ $Q(x)=x^{2}-2$ est le quotient et $P(-3)=0$ le reste
Exercice 12:
Soit le polynôme : $P(x)=x^{3}-2 x^{2}-5 x+6$
1) Effectuer la division euclidienne de $P(x)$ par $x+2$ et déterminer le quotient $Q(x)$ et le reste.
2) montrer que $Q(x)$ est divisible par $x-3$.
3) en déduire une factorisation du polynôme $P$ on polynômes de 1ere degrés.
1)

Donc: $Q(x)=x^{2}-4 x+3$ le reste 0
2) $Q(3)=0$ donc 3 est racine du polynôme $Q(x)$
Donc $Q(x)$ est divisible par $x-3$
3) On a: $P(x)=(x+2) \times\left(x^{2}-4 x+3\right)$
En effectuant la division euclidienne de $Q(x)$ par $x-3$
On aura : $Q(x)=(x-3) (x-1)$
Donc: $P(x)=(x+2) (x-3) (x-1)$
Exercice 13:
Soit: $P(x)=x^{3}-3 x^{2}-6 x+8$
1) Montrer que1 est racine du polynôme $P$
2) Montrer que $P(x)=(x-1) Q(x)$ Où $Q(x)$ est un polynôme a déterminer
3) Montrer que -2 est racine du polynôme $Q$
4) En déduire une factorisation du polynôme $P$ on polynômes de 1ere degrés
5) Résoudre dans $\mathbb{R}$ l’équation $P(x)=0$
1) On a $P(1)=1^{3}-3 \times 1^{2}-6 \times 1+8=1-3-6+8=0$
Alors 1 est racine du polynôme $P$
Donc $P(x)$ est divisible par $X-1$
2) Effectuons la division euclidienne de $P(x)$ par $x-1$ On trouve : $P(x)=(x-1)\left(x^{2}-2 x-8\right)$ (1)
Donc: $Q(x)=x^{2}-2 x-8$
3) On a : $Q(-2)=(-2)^{2}-2(-2)-8=4+4-8=0$
Donc -2 est racine du polynôme $Q$ Donc $Q(x)$ est divisible par $x+2$
4) Effectuons la division euclidienne de $Q(x)$ par $x+2$
On trouve : $Q(x)=(x+2)(x-4)$ (2)
D’après (1) et (2) on a : $P(x)=(x-1)(x+2)(x-4)$
5) $P(x)=0$ ssi $(x-1)(x+2)(x-4)=0$
ssi $x-1=0$ ou $x+2=0$ ou $x-4=0$
$P(x)=0 \quad$ ssi $x=1$ ou $x=-2$ ou $x=4$ les racines du polynôme $P(x)$
Donc : $S=\{-2 ; 1 ; 4\}$
Exercice 14:
Soit: $P(x)=2 x^{3}+3 x^{2}+a x+b$
Avec $\quad a \in \mathbb{R}$ et $b \in \mathbb{R}$
1) Déterminer $a$ et $b$ tels que :
a) $P(x)$ soit divisible par $x-2$
b) Le reste de la division euclidienne de $P(x)$ par $x-1$ est -12
2) Factoriser $P(x)$ dans ce cas.
1) $P(x)=2 x^{3}+3 x^{2}+a x+b$
a) $P(x)$ soit divisible par $x-2$ donc: $P(2)=0$
Donc: $2 \times 2^{3}+3 \times 2^{2}+a \times 2+b=0$
Donc: $2 a+b+28=0$ (1)
b) le reste de la division euclidienne de $P(x)$ par $x-1$ est -12
donc: $P(1)=-12$ donc : $a-b+17=0$ (2)
donc le couple $(a, b)$ est solution du système suivant :
$\left\{\begin{array}{l}2 a+b+28=0 \\ a-b+17=0\end{array}\right.$
On résolvant le système on trouve : $a=-11$ et $b=-6$
Donc: $P(x)=2 x^{3}+3 x^{2}-11 x-6$
2)Factorisation de $P(x)$ dans ce cas:
$P(x)$ est divisible par $x-2$ donc :

$P(x)=(x-2)\left(2 x^{2}+7 x+3\right)$
Exercice 15:
Soit: $P(x)=x^{3}-3 x+2$
1)a) calculer $P(1)$ et déterminer $Q(x)$ tel que :
$P(x)=(x-1) Q(x)$
b) Vérifier que $P(x)=(x+2)(x-1)^{2}$
2) Soit $\alpha$ un réel tel que : $1<\alpha<2$
Donner un encadrement de $\alpha+2$ et de : $(\alpha-1)^{2}$
Et en déduire que : $0<P(\alpha)<4$
1)a) $P(x)=x^{3}-3 x+2$
$P(1)=1^{3}-3 \times 1+2=1-3+2=0$
Donc $P(x)$ soit divisible par $x-1$
Effectuons la division euclidienne de $P(x)$ par $x-1$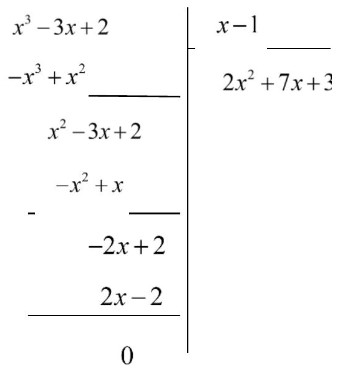
Donc : $P(x)=(x-1)\left(x^{2}+x-2\right)$
b) Vérifions que $P(x)=(x+2)(x-1)^{2}$ ?
$(x+2)(x-1)^{2}=(x+2)\left(x^{2}-2 x+1\right)$
$=x^{3}-2 x^{2}+x+2 x^{2}-4 x+2=x^{2}-4 x+2=P(x)$
2) $1<\alpha<2$ donc $3<\alpha+2<4$ (1)
Donc: $0<\alpha-1<1$ donc $0<(\alpha-1)^{2}<1$ (2)
D’après $(1)$ et $(2)$ on a alors : $0<(\alpha+2)(\alpha-1)^{2}<4$
Donc $0<P(\alpha)<4$
Exercice 16:
Soit: $P(x)=2 x^{4}-9 x^{3}+14 x^{2}-9 x+2$
1) Vérifier que 0 n’est pas racine du polynôme $P(x)$
2) Montrer que si $\alpha$ est racine du polynôme $P(x)$ alors $\frac{1}{\alpha}$
Est aussi racine du polynôme $P(x)$
3) Vérifier que 2 est racine du polynôme $P(x)$
4) En Effectuant la division euclidienne de $P(x)$ par $x-2$
Trouver un polynôme $Q(x)$ tel que :
$P(x)=(x-2) Q(x)$
5) En déduire que $Q\left(\frac{1}{2}\right)=0$
6) Déterminer les réels $a ; b ; c$ tel que :
$Q(x)=\left(x-\frac{1}{2}\right)\left(a x^{2}+b x+c\right)$
7) En déduire une factorisation du polynôme $P$ on polynômes de 1ere degrés
1) $P(0)=2 \neq 0$ Donc 0 n’est pas racine du polynôme $P(x)$
2) $P(x)$ racine du polynôme est $\alpha$
Ssi $P(\alpha)=0 \quad $ ssi $ \quad 2 \alpha^{4}-9 \alpha^{3}+14 \alpha^{2}-9 \alpha+2=0$
On calcul $P\left(\frac{1}{\alpha}\right)=$ ?
$P\left(\frac{1}{\alpha}\right)=2\left(\frac{1}{\alpha}\right)^{4}-9\left(\frac{1}{\alpha}\right)^{3}+14\left(\frac{1}{\alpha}\right)^{2}-9\left(\frac{1}{\alpha}\right)+2$
$P\left(\frac{1}{\alpha}\right)=2\left(\frac{1}{\alpha^{4}}\right)-9\left(\frac{1}{\alpha^{3}}\right)+14\left(\frac{1}{\alpha^{2}}\right)-9\left(\frac{1}{\alpha}\right)+2$
$P\left(\frac{1}{\alpha}\right)=\left(\frac{2}{\alpha^{4}}\right)+\left(\frac{-9 \alpha}{\alpha^{4}}\right)+\left(\frac{14 \alpha^{2}}{\alpha^{4}}\right)+\left(\frac{-9 \alpha^{3}}{\alpha^{4}}\right)+2 \frac{\alpha^{4}}{\alpha^{4}}$
$P\left(\frac{1}{\alpha}\right)=\frac{2-9 \alpha+14 \alpha^{2}-9 \alpha^{3}+2 \alpha^{4}}{\alpha^{4}}$
Et puisque $2 \alpha^{4}-9 \alpha^{3}+14 \alpha^{2}-9 \alpha+2=0$
Donc: $P\left(\frac{1}{\alpha}\right)=\frac{0}{\alpha^{4}}=0$
Donc : $\frac{1}{\alpha}$ Est aussi racine du polynôme $P(x)$
3) $P(2)=2 \times 2^{4}-9 \times 2^{3}+14 \times 2^{2}-9 \times 2+2=32-72+56-18+2$
$P(2)=2 \times 2^{4}-9 \times 2^{3}+14 \times 2^{2}-9 \times 2+2=32-72+56-18+2=0$
Donc : 2 est racine du polynôme $P(x)$
4) En Effectuant la division euclidienne de $P(x)$ par $x-2$
On trouve que: $P(x)=(x-2) \left(2 x^{3}-5 x^{2}+4 x-1\right)$
5) On a 2 est racine du polynôme $P(x)$
Donc: $\frac{1}{2}$ Est aussi racine du polynôme $P(x)$
Donc: $P\left(\frac{1}{2}\right)=0$ et puisque $P(x)=(x-2) Q(x)$
Alors: $\left(\frac{1}{2}-2\right) \times Q\left(\frac{1}{2}\right)=0$ or $\left(\frac{1}{2}-2\right) \neq 0$
Donc: $Q\left(\frac{1}{2}\right)=0$
6) En Effectuant la division euclidienne $\operatorname{de} Q(x)$ par $x-\frac{1}{2}$
On trouve : $Q(x)=\left(x-\frac{1}{2}\right)\left(2 x^{2}-4 x+2\right)$
Donc: $a=2$ et $b=-4$ et $c=2$
7) On a : $P(x)=(x-2) Q(x)$ et $Q(x)=\left(x-\frac{1}{2}\right)\left(2 x^{2}-4 x+2\right)$
Donc : $P(x)=(x-2)\left(x-\frac{1}{2}\right)\left(2 x^{2}-4 x+2\right)$
On factorise aussi : $2 x^{2}-4 x+2$
On remarque que 1 est racine
en Effectuant la division euclidienne de $2 x^{2}-4 x+2$ par $(x-1)$ On trouve :
$2 x^{2}-4 x+2=(x-1)(2 x-2)$ finalement: $P(x)=(x-2)\left(x-\frac{1}{2}\right)(x-1)(2 x-2)$
$P(x)=2(x-2)\left(x-\frac{1}{2}\right)(x-1)(x-1)$
$P(x)=(x-2)(2 x-1)(x-1)^{2}$
Exercice 17:
Soit le polynôme suivant (E) : $P(x)=x^{3}-\sqrt{3} x^{2}-4 x+4 \sqrt{3}$
1) Montrer que -2 est racine du polynôme $P(x)$
2) Montrer que: $P(x)=(x+2)\left(x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}\right)$
3) On pose : $Q(x)=x^{2}-(\sqrt{3}+2) x+2 \sqrt{3} \quad$ et soit $\Delta$ son discriminant
a) Vérifier que : $\Delta=(\sqrt{3}-2)^{2}$
b) Résoudre dans $\mathbb{R}$ l’équation : $Q(x)=0$
4) En déduire les solutions de l’équation : $x-(\sqrt{3}+2) \sqrt{x}+2 \sqrt{3}=0$
5) Résoudre dans $\mathbb{R}$ l’équation $P(x)=0$
6) Résoudre dans $\mathbb{R}$ l’inéquation $P(x) \geq 0$
1) $P(-2)=(-2)^{3}-\sqrt{3}(-2)^{2}-4(-2)+4 \sqrt{3}$
$P(-2)=-8-4 \sqrt{3}+8+4 \sqrt{3}=0$ Donc : -2 est racine du polynôme $P(x)$
2) $(x+2)\left(x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}\right)=x^{3}-(\sqrt{3}+2) x^{2}+2 \sqrt{3} x+2 x^{2}-2(\sqrt{3}+2) x+4 \sqrt{3}$
$ =x^{3}-\sqrt{3} x^{2}-2 x^{2}+2 \sqrt{3} x+2 x^{2}-2 \sqrt{3} x-4 x+4 \sqrt{3} $
$ =x^{3}-\sqrt{3} x^{2}-4 x+4 \sqrt{3}=P(x)$
3) a) On pose : $Q(x)=x^{2}-(\sqrt{3}+2) x+2 \sqrt{3} \quad a=1$ et $b=-(\sqrt{3}+2)$ et $c=2 \sqrt{3}$
$\Delta=b^{2}-4 a c=(-(\sqrt{3}+2))^{2}-4 \times 2 \sqrt{3} \times 1=(\sqrt{3}+2)^{2}-8 \sqrt{3}$
$\Delta=\sqrt{3}^{2}+2 \times 2 \times \sqrt{3}+2^{2}-8 \sqrt{3}=\sqrt{3}^{2}-4 \sqrt{3}+2^{2}=(\sqrt{3}-2)^{2}$
b) $Q(x)=x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}$
Puisque : $\Delta \succ 0$ donc il y’a deux racines :
$x_{1}=\frac{\sqrt{3}+2+\sqrt{(\sqrt{3}-2)^{2}}}{2 \times 1}=\frac{\sqrt{3}+2+|\sqrt{3}-2|}{2 \times 1}$ et $x_{2}=\frac{\sqrt{3}+2-\sqrt{(\sqrt{3}-2)^{2}}}{2 \times 1}=\frac{\sqrt{3}-2-|\sqrt{3}-2|}{2 \times 1}$
Or on a: $2 \succ \sqrt{3} \operatorname{car}(2)^{2} \succ(\sqrt{3})^{2}$
donc : $\sqrt{3}-2 \prec 0$
Par suite: $|\sqrt{3}-2|=-(\sqrt{3}-2)=2-\sqrt{3}$
Donc: $x_{1}=\frac{\sqrt{3}+2+2-\sqrt{3}}{2 \times 1}=2$ et $x_{2}=\frac{\sqrt{3}+2+\sqrt{3}-2}{2 \times 1}=\sqrt{3} \quad$ par suite: $S=\{\sqrt{3}, 2\}$.
4) $x-(\sqrt{3}+2) \sqrt{x}+2 \sqrt{3}=0$ est équivalente à: $(\sqrt{x})^{2}-(\sqrt{3}+2) \sqrt{x}+2 \sqrt{3}=0$.
On pose : $X=\sqrt{x}$ et on a donc: $X^{2}-(\sqrt{3}+2) X+2 \sqrt{3}=0$
Mais d’après 3)b) on a : $X_{1}=\sqrt{3}$ et $X_{2}=2$
Qui Signifie que: $\sqrt{x_{1}}=\sqrt{3}$ et $\sqrt{x_{2}}=2$
donc: $\left(\sqrt{x_{1}}\right)^{2}=(\sqrt{3})^{2}$ et $\left(\sqrt{x_{2}}\right)^{2}=(2)^{2}$
Qui Signifie que: $x_{1}=3$ et $x_{2}=4$ par suite: $S=\{3,4\}$
5) On a: $P(x)=(x+2)\left(x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}\right)$
$P(x)=0$ Signifie $x+2=0$ ou $x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}=0$
Signifie que : $x_{0}=-2$ ou $x_{1}=\sqrt{3}$ ou $x_{2}=2$
Par suite: $S=\{-2,2, \sqrt{3}\}$
6) $P(x) \geq 0$ Signifie que: $(x+2)\left(x^{2}-(\sqrt{3}+2) x+2 \sqrt{3}\right) \geq 0$
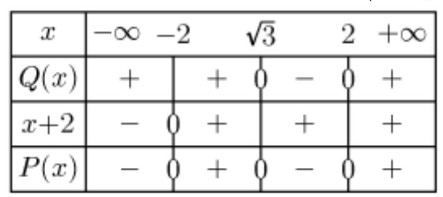
$S=[-2 ; \sqrt{3}] \cup[2 ;+\infty[$
Exercice 18:
Soit le polynôme : $P(x)=2 x^{3}-x^{2}-13 x-6$
1) Quels sont les diviseurs entiers relatifs du terme constant 6 ?
2) Déterminer (en cas d’existence) les racines relatives du polynôme $P(x)$
3) Factoriser le polynôme $P(x)$ en un produit de monômes
4) Résoudre dans $\mathbb{R}$ l’inéquation $P(x) \geq 0$
1) Les diviseurs entiers relatifs du terme constant 6 sont : $- 6 ; -3; – 2 ; -1; 1; 3; 3$
2) S’il existe une racine $a \in \mathbb{Z}$ du polynôme $P(x)$ alors : $P(a)=0$
C’est-à-dire : $2 a^{3}-a^{2}-13 a-6=0$
C’est-à-dire : $a\left(2 a^{2}-a-13\right)=6$
C’est-à-dire : $a$ est un diviseur de 6
C’est-à-dire : $a \in\{-6 ;-3 ;-2 ;-1 ; 1 ; 2 ; 3 ; 6\}$
Maintenant il ne nous reste plus qu’à tester chacun de ces nombres s’il est racine :
On trouve seulement: $\left\{\begin{array}{l}P(-2)=2(-2)^{3}-(-2)^{2}-13(-2)-6=0 \\ P(3)=2 \times 3^{3}-3^{2}-13 \times 3-6=0\end{array}\right.$
Donc: les racines relatives du polynôme $P(x)$ sont : – 2 et 3
3) Factorisons le polynôme $P(x)$ en un produit de monômes
On a :-2 est racine du polynôme $P(x)$ donc $P(x)$ est divisible par $x+2$
II existe donc un polynôme $Q(x)$ tel que : $P(x)=(x+2) Q(x)$
Mais aussi on a : 3 est racine du polynôme $P(x)$ c’est-à-dire : $P(3)=(3+2) Q(3)=0$
C’est-à-dire : $Q(3)=0$
C’est-à-dire : 3 est racine du polynôme $Q(x)$
C’est-à-dire : $Q(x)$ est divisible par $x-3$
C’est-à-dire : Il existe un polynôme $R(x)$ tel que : $Q(x)=(x-3) R(x)$
Donc: $P(x)=(x+2)(x-3) R(x)$
C’est-à-dire : $P(x)$ est divisible par $(x+2)(x-3)=x^{2}-x-6$
Donc : $P(x)=\left(x^{2}-x-6\right) R(x)$
Mais le $\operatorname{deg} P=3$ et $\operatorname{deg}\left(x^{2}-x-6\right)=2$
Par suite : $\operatorname{deg} R=1$
Donc: $R(x)=a x+b$
$P(x)=\left(x^{2}-x-6\right)(a x+b)=a x^{3}+b x^{2}-a x^{2}-b x-6 a x-6 b$
$P(x)=a x^{3}+(b-a) x^{2}-(b+6 a) x-6 b$
Et puisque : $P(x)=2 x^{3}-x^{2}-13 x-6$
Par identification on a : $\left\{\begin{array}{l}a=2 \\ b-a=-1 \\ -6 b=-6 \\ -(b+6 a)=-13\end{array} \quad\right.$
Signifie que $\left\{\begin{array}{l}a=2 \\ b=1\end{array}\right.$
Donc: $P(x)=(x+2)(x-3)(2 x+1)$
4) $P(x) \geq 0$ Signifie: $(x+2)(x-3)(2 x+1) \geq 0$
Donc le tableau de signe suivant :
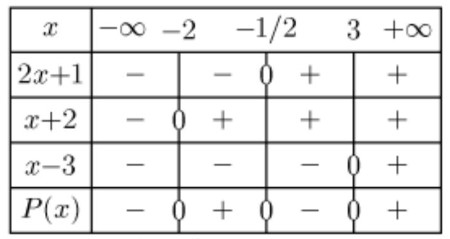
Donc : $S=\left[-2 ; \frac{1}{2}\right] \cup[3 ;+\infty[$
