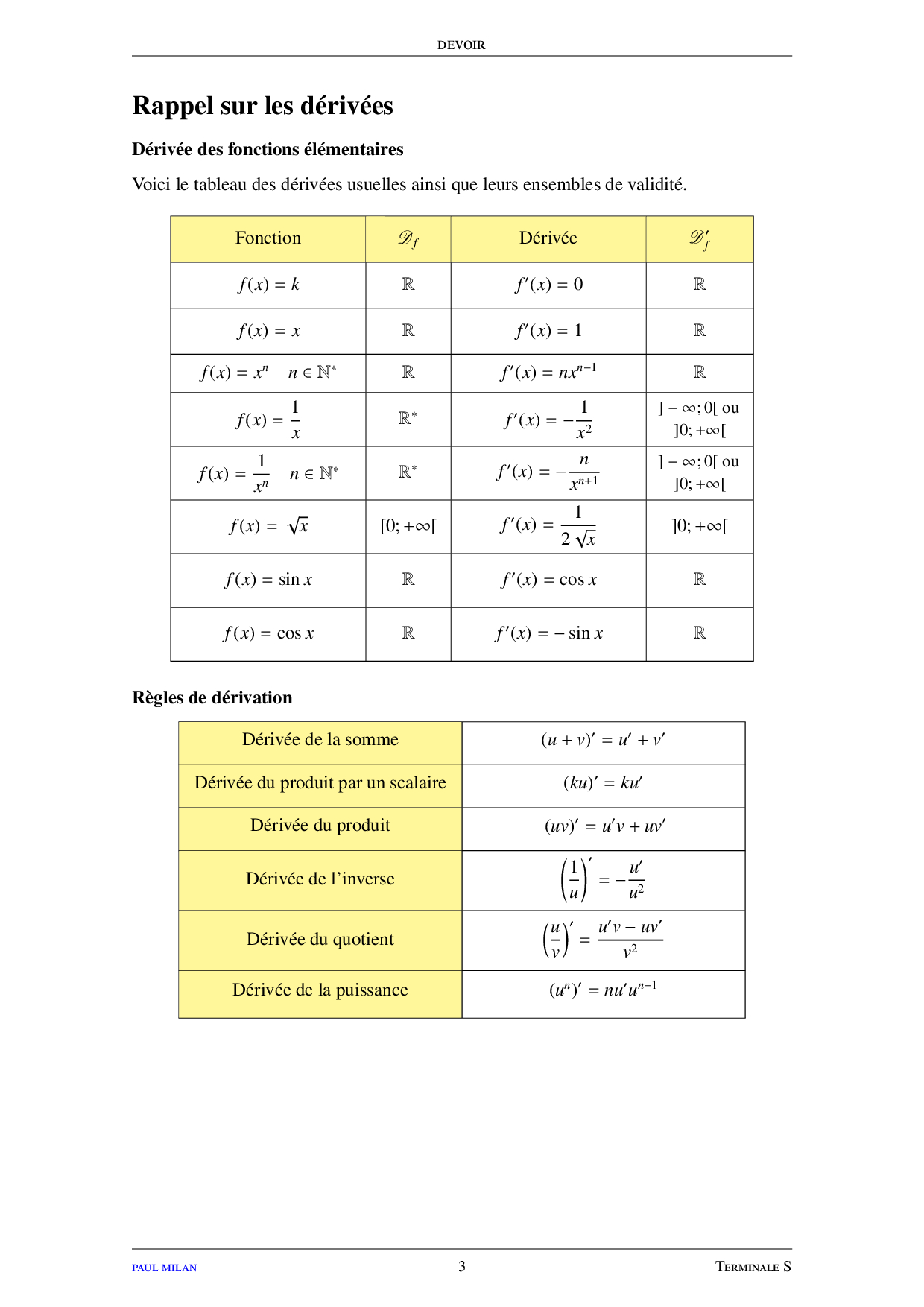
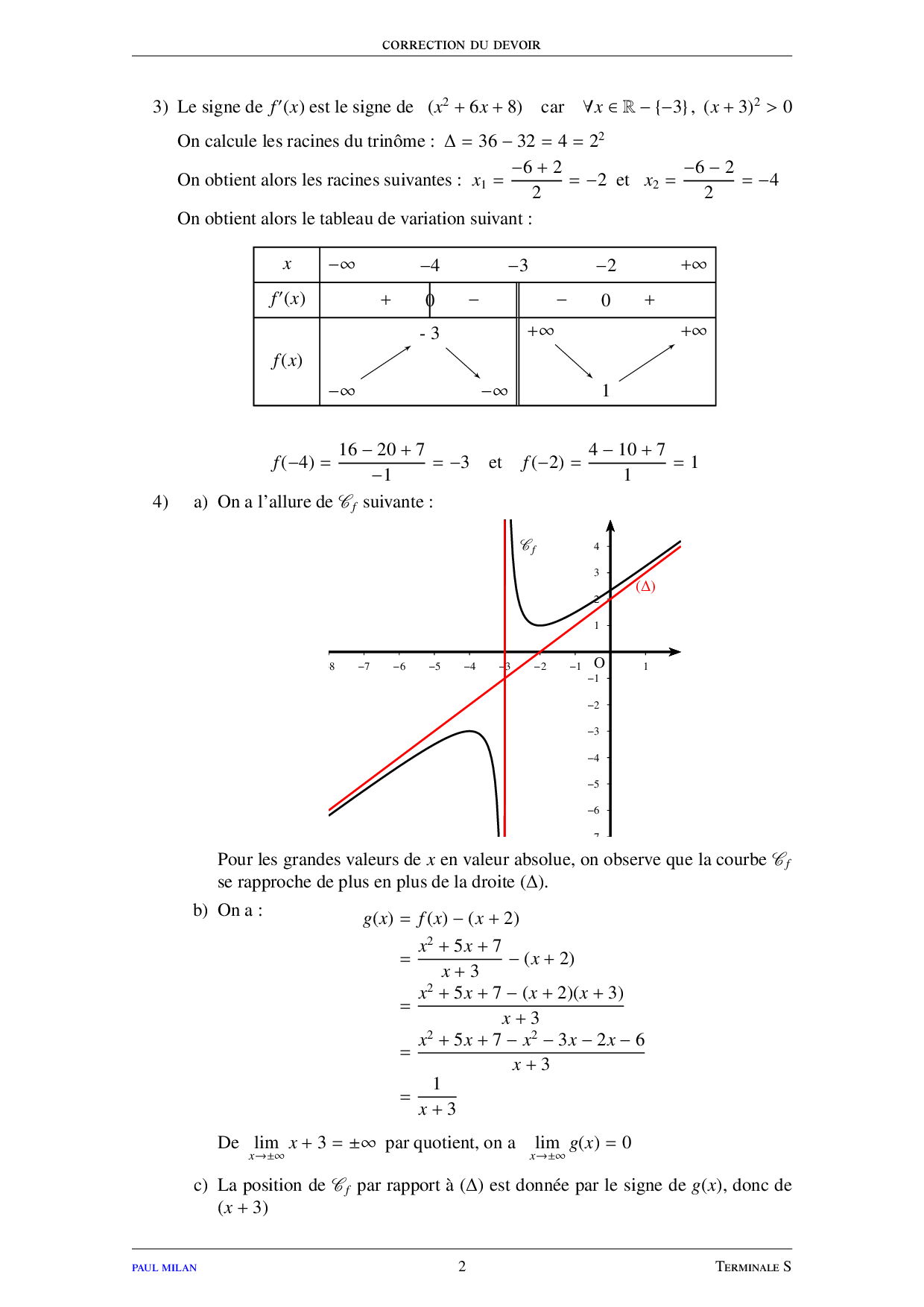
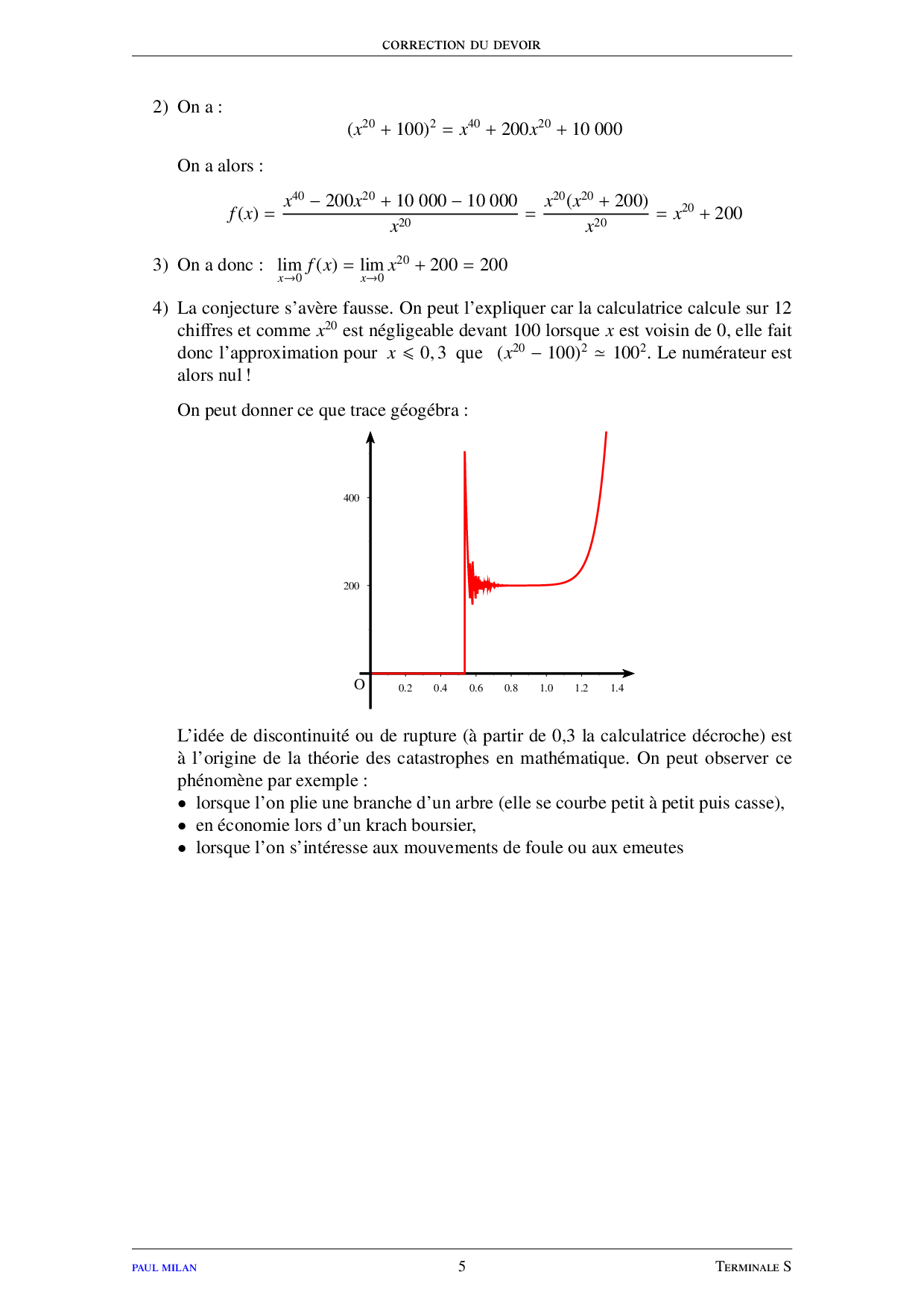
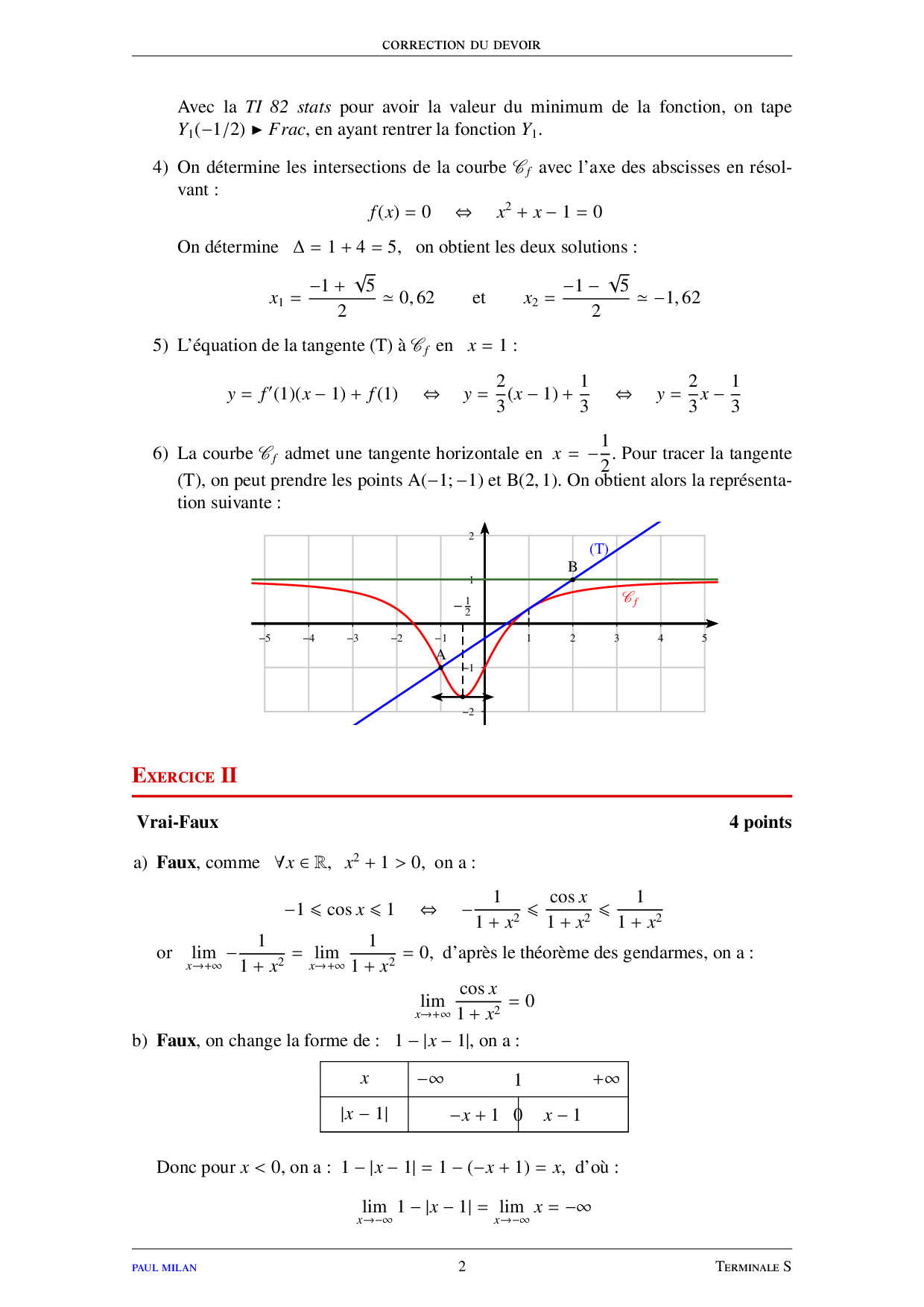
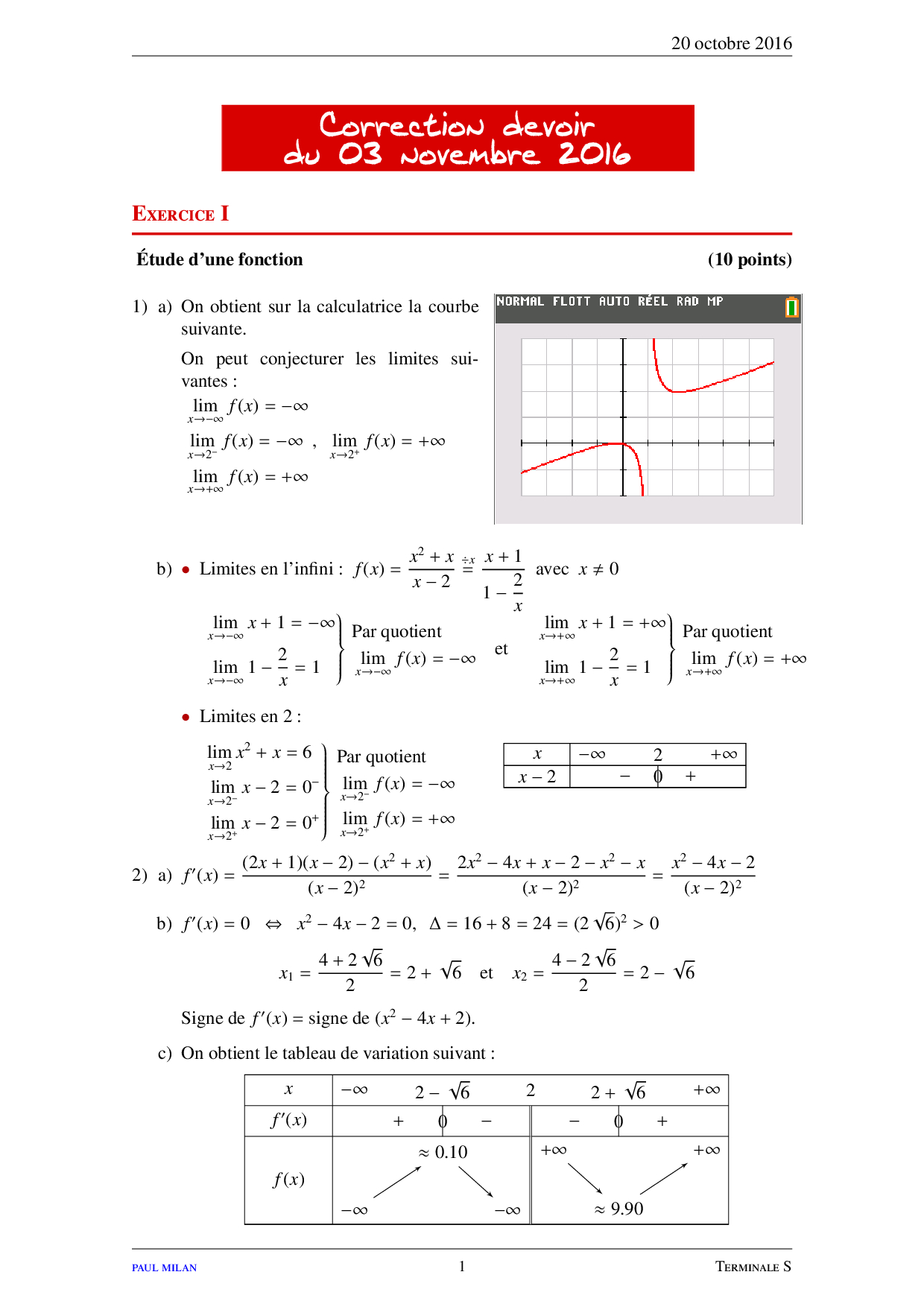
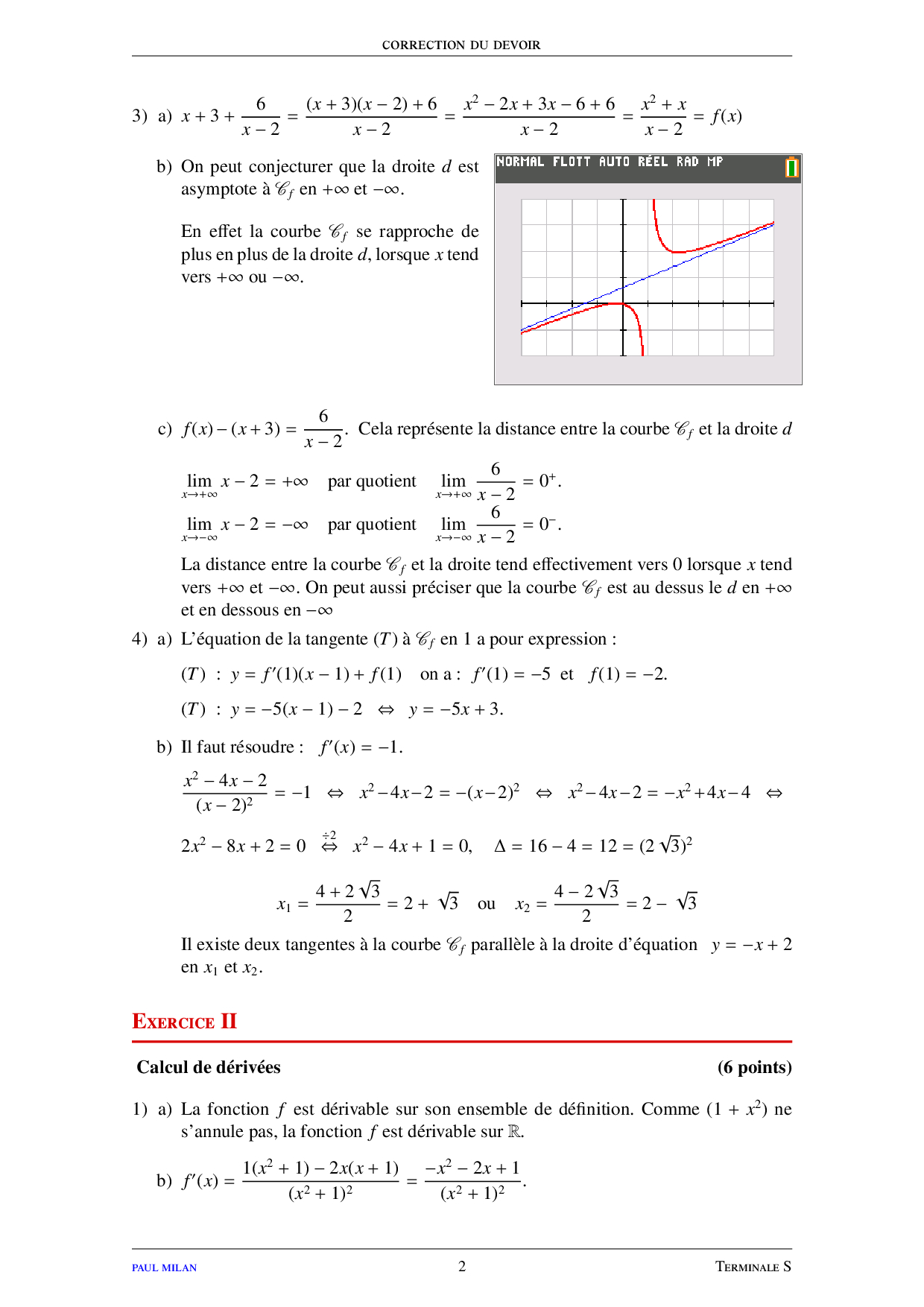
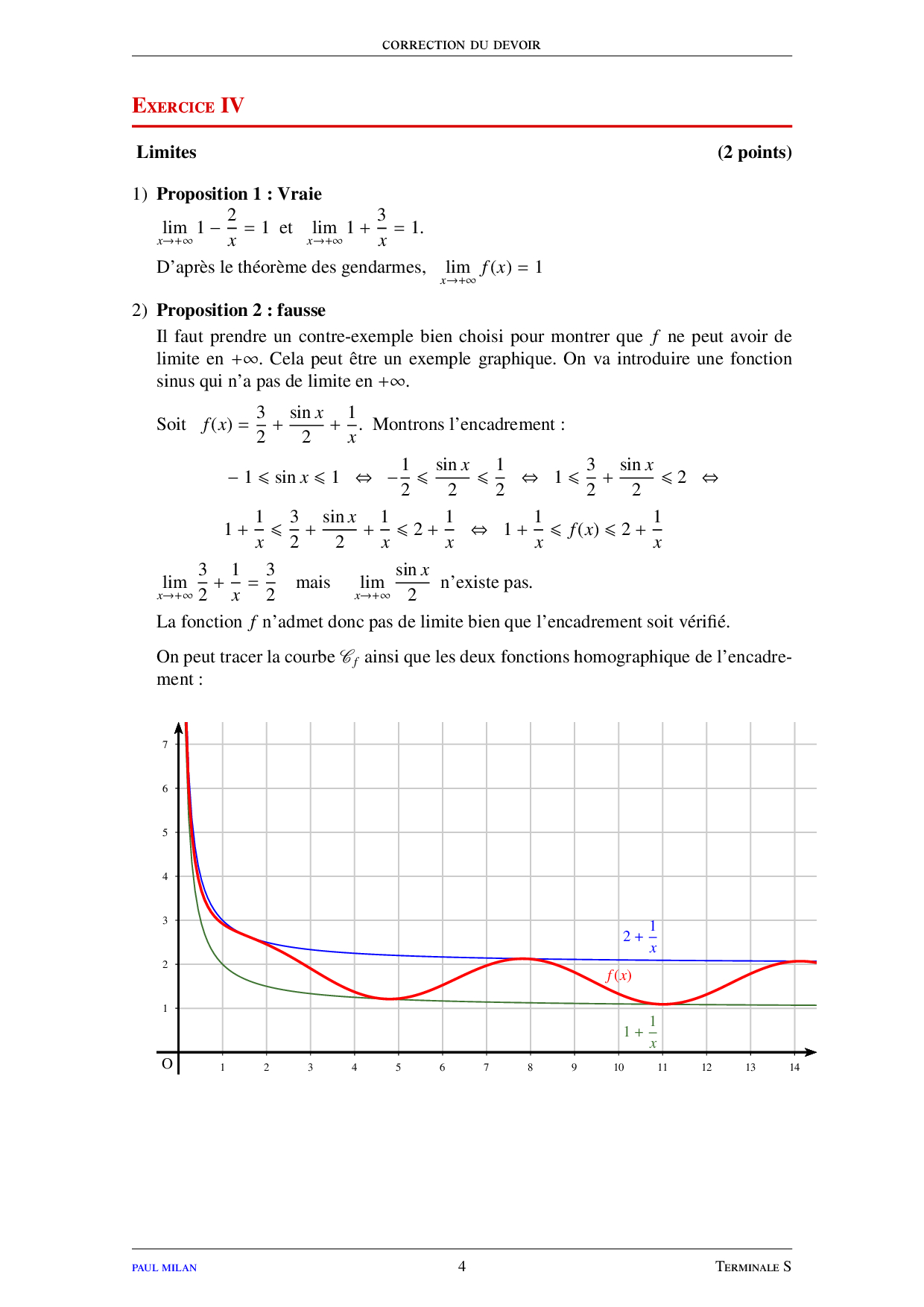
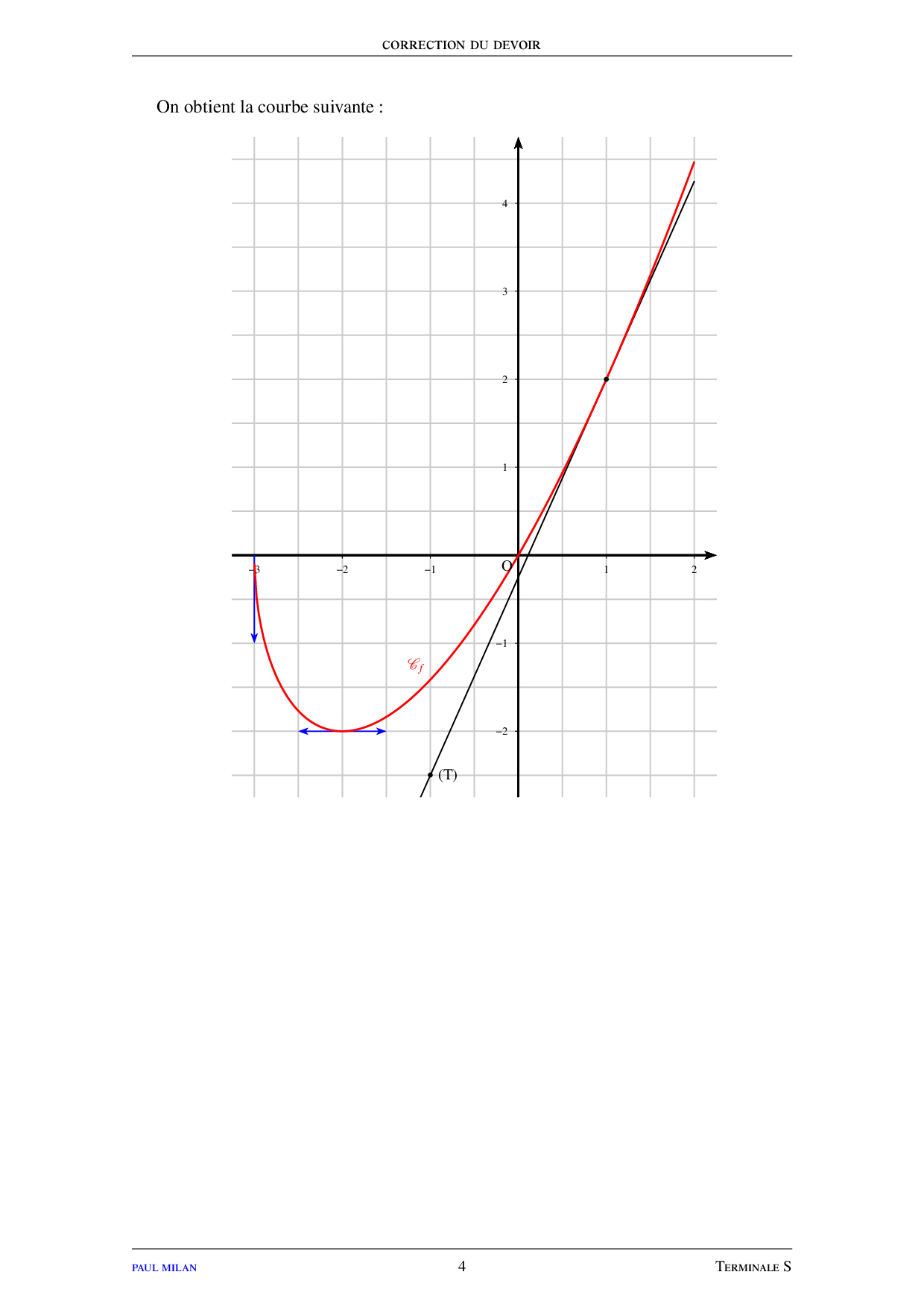
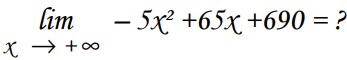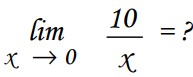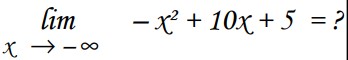Limites de fonctions

LIMITES des FONCTIONS

a) Exemples :
1- Il y a actuellement 50 filles et 60 garçons et il arrive un couple (fille, garçon ) par minute
Que devient le pourcentage de filles si l ’on attend très longtemps ?

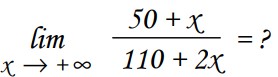
2- On partage équitablement 1 million d ’euros entre x personnes !
Que devient la part de chacun s’il y a beaucoup de personnes ?

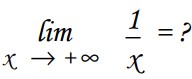
3-  Si prix du repas est de x euros , le bénéfice du restaurateur est de B(x) = – 5x² +65x +690
Que devient le bénéfice s’ il augmente beaucoup le prix ? 

4- Avec 10 litres d ’eau, on rempli des verres de x ml !
Que devient le nombre de verres que l’on peut remplir quand le verre est de plus en plus petit ?



5-  Il se déplace sur un axe gradué et son abscisse en fonction du temps est donnée par
A(x) = – x² + 10x + 5 .
Que devient son abscisse si l ’ on remonte longtemps dans le passé ? 


b) Remarques :
Les fonctions permettent de « modéliser » certains phénomènes, de décrire l’ évolution
de certains d’entre eux dans le temps par exemple. ( variations de la température moyenne
de la terre, variation de la population d’un pays…).
On s’intéresse parfois à ce que devient le phénomène loin dans le passé ou loin dans le futur
ou encore, sur un voisinage d’une date précise. Ce type de questions a fait naître la notion de
limites d’une fonction en + ∞ en – ∞ ou en un nombre a ( a = 0, par exemple ).
Il est nécessaire, de connaître et de maîtriser certains savoir-faire concernant cette notion.