Matrices et suites Maths 1ère S exercices corrigés

  1 Introduction
Le modèle d’Ehrenfest fut défini en 1907 par Paul Ehrenfest, physicien, et son
épouse Tatiana, mathématicienne, pour illustrer certains paradoxes apparaissant
dans l’étude théorique du comportement de systèmes physiques comportant un
grand nombre de particules.
Pour les physiciens,l’un des objectifs était de lever le « paradoxe » de l’irréversibilité.
L’irréversibilité est une évidence à notre échelle : la plupart des phénomènes
macroscopiques ont une orientation dans le temps bien définie. Le second principe
de la thermodynamique décrit cette irréversibilité : un système isolé évolue
vers son maximum d’entropie et l’entropie ne diminue jamais ! L’entropie décrit
le « désordre » d’un système c’est à dire le quotient de la variation de chaleur par
une température.
Cependant les lois de la dynamique des particules sont toutes réversibles et aucune
des transformations des particules n’est irréversible. Les physiciens voulaient
donc montrer comment, à partir de particules aux évolutions réversibles,
on pouvait obtenir, en combinant ces évolutions, une situation macroscopique irréversible.
Dans le modèle d’Ehrenfest, chaque particule a un comportement totalement
réversible et la situation macroscopique est la superposition d’un grand
nombre de particules identiques. Il s’agissait donc pour le couple Ehrenfest de
prouver qu’il n’y avait pas besoin de modifier les lois de la physique des particules
pour décrire l’irréversibilité du monde.
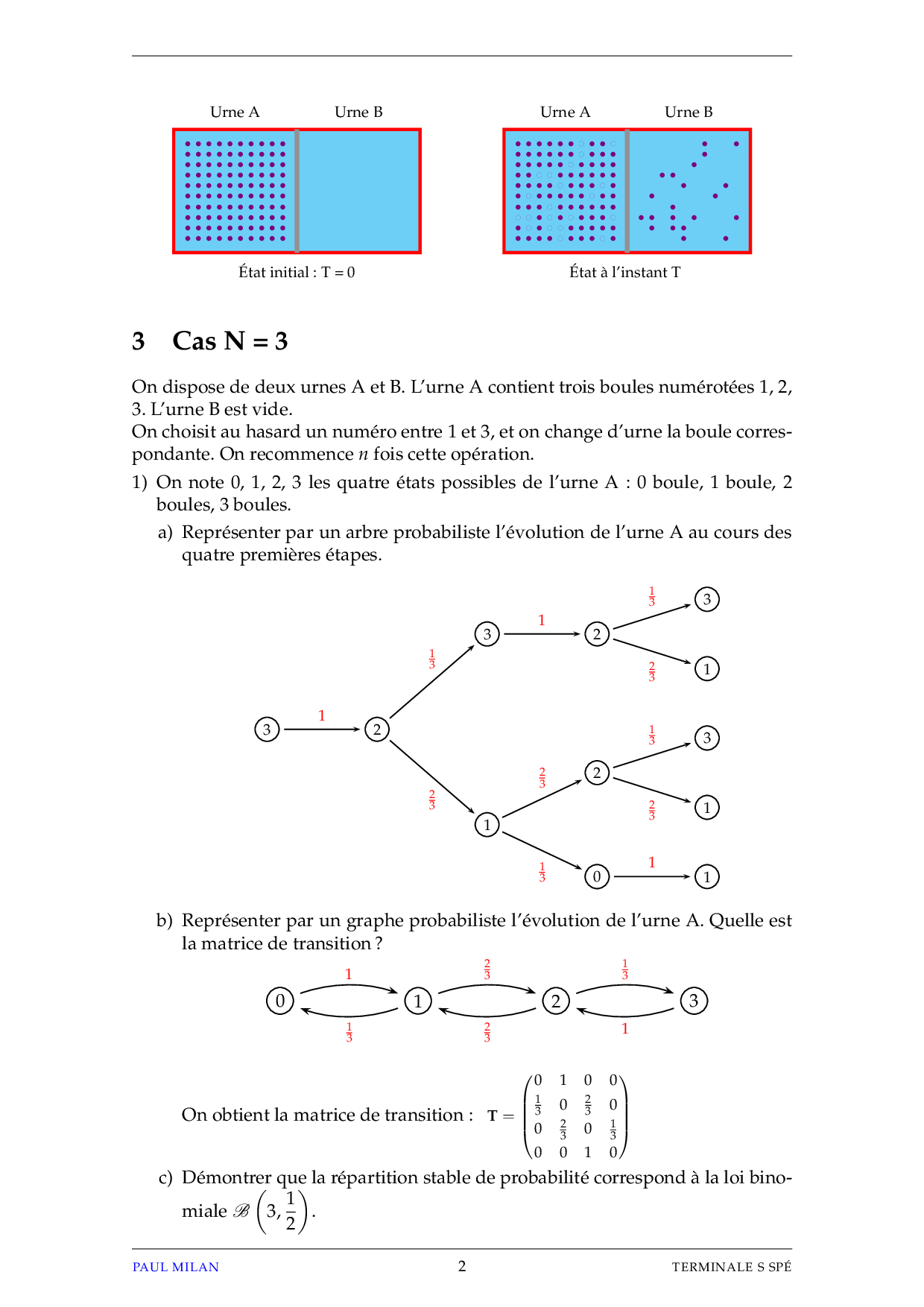
  2 L’expérience
On considère d’une part deux urnes A et B, et d’autre part N boules, numérotées
de 1 à N, réparties les unes dans l’urne A, les autres dans l’urne B.
Expérience d’Ehrenfest : Expérience consistant à tirer au hasard un numéro I
compris entre 1 et N et de transférer la boule numéro I dans l’urne où elle n’était
pas.
Le processus aléatoire d’Ehrenfest consiste à discrétiser le temps et de répéter
à chaque instant l’expérience d’Ehrenfest. On s’intéresse au nombre de boules
présentes dans l’urne A à un instant donné appartenant à N
On suppose qu’au début de l’expérience l’urne A contient toutes les boules.