Mesure de la masse des solides et des liquides exercices corrigés
La masse des liquides et des solides
I. Notion de la masse.
– La masse d’un corps est une grandeur physique liée à la quantité de la matière, on la symbolise par la lettre $\mathbf{m}$.
– Dans le système international, l’unité de la masse est le kilogramme $Kg$.
– L’unité usuelle de la masse est le gramme $g$.
• Tableau de conversion :

Application :
Convertir:
$2,5 \mathrm{~g}=……..\mathrm{~dg}$
$45 \mathrm{~kg}=……..\mathrm{~t}$
$ 0,25 \mathrm{~cg} =…….. \mathrm{~mg}$
Solution :
$2,5 \mathrm{~g}=25 \mathrm{~dg}$
$45 \mathrm{~kg}=0,045 \mathrm{~t}$
$ 0,25 \mathrm{~cg} =25 \mathrm{~mg}$
II. Mesure de la masse d’un solide.
– Pour mesurer la masse d’un corps, on utilise une balance. Il existe différents types des balances:

– Pour mesurer la masse d’un corps solide à l’aide d’une balance de Roberval on utilise les masses marquées et on suit les étapes suivantes:
• On réalise l’équilibre des plateaux lorsqu’ils sont vides.
• On place le corps solide sur l’un des plateaux et les masses marquées sur l’autre plateau.
• On réalise l’équilibre des plateaux de nouveau.
• La masse du solide est la somme des masses marquées.
Exemple: Masse d’une boite.

– La masse de la boite est : $\mathbf{m = 1 0 g + 5 0 g + 1 0 0 g + 1 0 0 g = 2 6 0 g}$
III. Mesure de la masse d’un liquide.
Pour mesurer la masse d’un liquide on utilise une balance et un récipient, puis on suit les étapes suivantes :
• On mesure la masse du récipient et on écrit $\mathrm{m}_{1}$.
• On verse doucement le liquide dans le récipient .
• On mesure la masse de l’ensemble \{récipient + liquide \} et on écrit $\mathrm{m}_{2}$.
• La masse du liquide est : $\mathbf{m = m _ { 2 }}-\mathbf{m}_{1}$.
Exemple: Masse de l’eau liquide.

– La masse du bécher vide est : $\mathbf{m}_{\mathbf{1}}=\mathbf{4 6 , 7 g}$
– La masse de l’ensemble est : $\mathbf{m}_{\mathbf{2}}=\mathbf{9 8 , 7 g}$
– La masse de l’eau liquide est : $m=m_{2}-m_{1}=98.7 g-46.7 g=52 g$
Remarque:
– Si on change la forme du corps sa masse ne change pas.
– L’utilisation du bouton « TARE » dans une balance électronique permet de remettre l’indication de la balance à zéro pour ne mesurer que la masse du contenu.
Exercice 1:
$1)$ Cocher la case correspondant à la réponse correcte.
$\begin{array} {|r|r|}\hline Grandeur \quad physique & Symbole \quad & Unité \quad internationale & Instrument \quad de \quad mesure \\ \hline La \quad masse & … …………… & … …………… & ……………… \\ \hline \end{array}$
$2)$ Convertir à l’unité demandée
$12 \mathrm{Kg} =\cdots \mathrm{g}$
$20 \mathrm{t} =\cdots \mathrm{Kg} $
$560 \mathrm{~g} =\cdots \mathrm{mg} $
$0.75 d a g =\cdots \mathrm{mg} $
$1.2 \mathrm{~g} =\cdots \mathrm{Kg} $
$1 \mathrm{~g} =\cdots \mathrm{Kg}$
$200 \mathrm{mg} =\cdots \mathrm{g} $
$4.5 \mathrm{Kg} =\cdots \mathrm{hg} $
$340 \mathrm{mg} =\cdots \mathrm{g}$
$1)$ Cocher la case correspondant à la réponse correcte.
$\begin{array} {|r|r|}\hline Grandeur \quad physique & Symbole \quad & Unité \quad internationale & Instrument \quad de \quad mesure \\ \hline La \quad masse & \mathrm{~m} \quad & \mathrm{~Kg} \quad & La \quad balance \quad \\ \hline \end{array}$
$2)$ Je convertis :
$12 Kg =12000 \mathrm{~g}$
$560 g =560000 \mathrm{mg}$
$1.2 g =0.0012 \mathrm{Kg}$
$20 t =20000 \mathrm{Kg} $
$0.75 d a g =7500 \mathrm{mg} $
$1 g =0.001 \mathrm{Kg}$
$200 \mathrm{mg} =0.2 \mathrm{~g} $
$4.5 \mathrm{Kg} =45 \mathrm{hg} $
$340 \mathrm{mg} =0.34 \mathrm{~g}$
Exercice 2:
Placer les mots suivants dans la bonne place : Tare, matière, électronique, balance de Roberval, kilogramme.
– La masse d’un objet représente la quantité de $………………………..$ qui forme l’objet.
– Dans le système international, la masse s’exprime en $………………………………..$ de symbole $kg$
– Il existe deux catégories de balances : $………………………$ et $ …………………………………………….$
– Toutes les balances électroniques ont une fonction appelée : $…………………..$
Exercice 3:
On réalise les pesées suivantes :
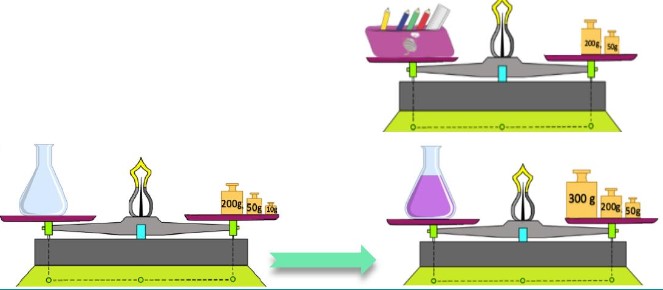
$1)$ Calculer en $(g)$ la masse $\mathbf{m}$ ‘ de la trousse.
$2)$ Déterminer la masse $\boldsymbol{m}_{\mathbf{1}}$ du récipient vide.
$3)$ Déterminer la masse $\boldsymbol{m}_{\mathbf{2}}$ du récipient + le liquide.
$4)$ Déduire la masse $\boldsymbol{m}$ du liquide.
Exercice 4:
Un vendeur des fruits a fait les pesées suivantes :

$\Rightarrow$ Déterminer la masse de la pomme, de la poire et le banane.
Exercice 5:
Pour mesurer la masse d’un liquide, on utilise une balance électronique et une éprouvette, puis on réalise les expériences représentées dans la figure ci-dessous.

$1)$ Déterminer la masse de l’éprouvette.
$2)$ Déterminer la masse de l’ensemble {éprouvette + liquide}.
$3)$ Déduire la masse du liquide.
Exercice 6:
Avec une balance Roberval, des masses marquées, une tare et un corps (A), on réalise les deux pesées suivantes :
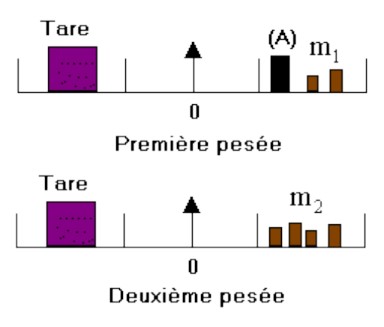
On donne : $m_{1}=55 \mathrm{~g}$ et $m_{2}=80 \mathrm{~g}$ .
$1)$ déterminer la masse de la tare ?
$2)$ déterminer la masse du corps (A) ?
Exercice 7:
Une bouteille vide pèse $60 g$. plein d’huile, elle pèse $1900 g$.
Calculez la masse d’huile introduit dans cette bouteille.
Exercice 8:
Une maman se pèse en tenant son bébé dans les bras : le cadran de la balance indique $59 kg 600 g$.
Elle se pèse ensuite toute seule : le cadran indique alors $54 kg 200 g$.
Combien pèse le bébé ?
Exercice 9:
Sur un pot de confiture, Ahmed lit l’indication suivante : $« 350g net »$. Par curiosité, avant d’entamer le pot, il le pose sur la balance et trouve une masse de $520g$.
$1)$ Comment expliquer la différence entre la masse lue sur la balance et celle indiquée sur le pot ?
$2)$ Que signifie le terme « net » sur l’étiquette ?
$3)$ Quelle est la masse de la confiture ? Du pot ? Justifier.
Mesure de la masse des solides et des liquides exercices corrigés
