Mesure du volume des solides et des liquides exercices corrigés
Volume des liquides et des solides
I – Notion de volume :
1 – Définition du volume :
Le volume d’un corps représente le lieu occupé par ce corps dans l’espace.
Le volume d’un corps est symbolisé par la lettre $V$.
2- Unités de volume et de capacité :
– L’unité internationale du volume est le mètre cube, son symbole est $\mathrm{m}^{3}$.
– La capacité d’un récipient est le volume maximal que peut contenir ce récipient.
– L’unité usuelle de la capacité est le litre de symbole $L$.
– La relation entre les unités de volume et celles de capacités est résumé dans le tableau suivant :
$\begin{array} {|r|r|}\hline & & \mathrm{m}^{3} & & & \mathrm{dm}^{3} & & & \mathrm{cm}^{3} & & & \mathrm{mm}^{3} \\ \hline & & KL & hL & daL & L & dL & cL & mL & & & \\ \hline & & & & & 4 & 5 & 1 & 8 & & & \\ \hline & & & & & 7 & 2 & 3 & & & & \\ \hline & & & & & & 1 & 2 & 5 & & & \\ \hline & & & 1 & 5 & 0 & & & & & & \\ \hline & & & & & 0 & 0 & 5 & & & & \\ \hline & 6 & 9 & & & & & & & & &\\ \hline \end{array}$
Application 1 : Convertir les volumes suivants aux unités demandées :
$4518 \mathrm{~cm}^{3}=………. \mathrm{~L}$
$ 150 \mathrm{~L}=………. \mathrm{dm}^{3}$
$7,23 \mathrm{dm}^{3}=………. \mathrm{~mL}$
$ 0,05 \mathrm{~L}=………. \mathrm{cm}^{3}$
$69 \mathrm{m}^{3}=………. \mathrm{~L}$
Réponse :
$4518 \mathrm{~cm}^{3}=4,518 \mathrm{~L}$
$ 150 \mathrm{~L}=150 \mathrm{dm}^{3}$
$7,23 \mathrm{dm}^{3}=7230 \mathrm{~mL}$
$ 0,05 \mathrm{~L}=50 \mathrm{cm}^{3}$
$69 \mathrm{m}^{3}=69000 \mathrm{~L}$
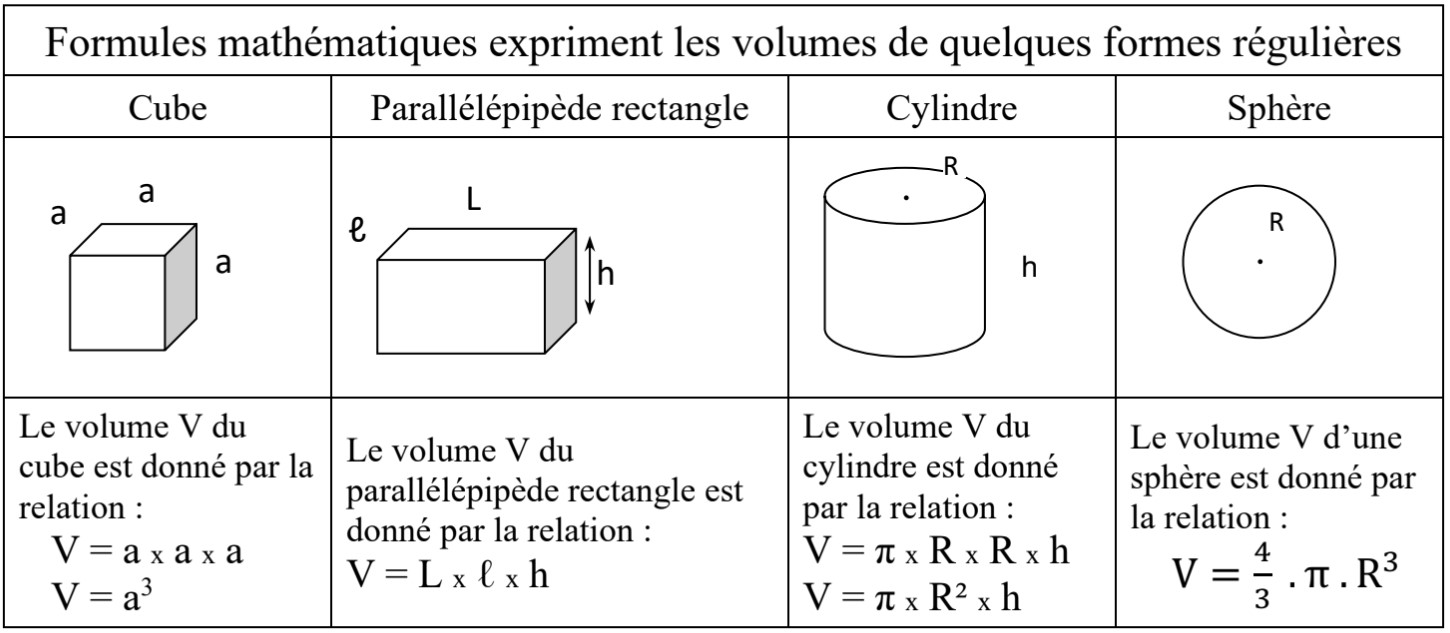
II – Calcul du volume d’un solide de forme géométrique simple :
Pour calculer le volume d’un solide de forme géométrique simple, il suffit d’utiliser la formule mathématique correspondante à la forme du solide.
Exemple :
Application 2 :
Calculer le volume d’un parallélépipède rectangle dont les dimensions sont:
La longueur: $\mathrm{L}=10 \mathrm{~cm}$, la largeur : $\ell=6 \mathrm{~cm}$, la hauteur : $\mathrm{h}=35 \mathrm{~mm}$.
Réponse :
On a: $\quad \mathrm{V}=\mathrm{L} \times \ell \times \mathrm{h}$
Application numérique : $\mathrm{V}=10 \mathrm{~cm} \times 6 \mathrm{~cm} \times 35 \mathrm{~mm}$
Conversion : $35 \mathrm{~mm}=3,5 \mathrm{~cm}$
Donc: $\mathrm{V}=10 \mathrm{~cm} \times 6 \mathrm{~cm} \times 3,5 \mathrm{~cm}$
$\mathrm{V}=210 \mathrm{~cm}^{3}$
III – Mesure de volume d’un liquide :
Pour mesurer le volume d’un liquide avec une éprouvette graduée, on suit les étapes suivantes:
$a – $Connaitre l’unité du volume inscrite sur l’éprouvette ( Le millilitre $mL$ ).
$b -$ Déterminer le volume correspondant à une petite division.
$c -$ Verser le liquide dans l’éprouvette sans perte.
$d -$ Mètre l’éprouvette sur un plan horizontale.
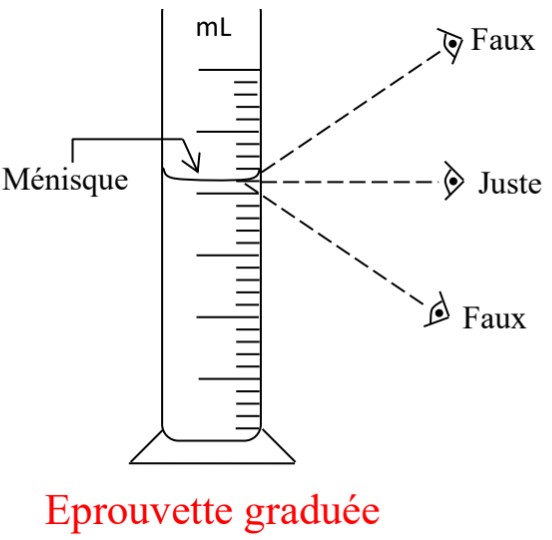
$e -$ Placer l’œil sur l’horizontale passant par le bas du ménisque.
$f -$ Écrire le résultat suivie de l’unité correspondante.
Application 3 :
Déterminer le volume du liquide contenu dans chaque éprouvette graduée.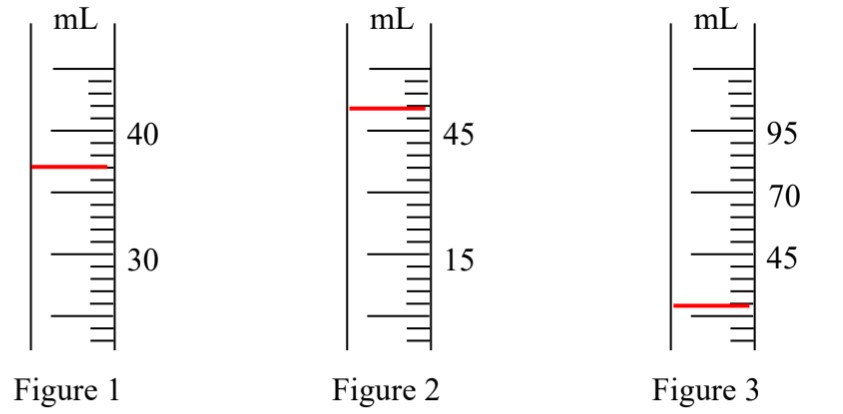
Solution:
$\star$ Figure 1:
– Calculons la valeur d’une division :
$V_{d}=\frac{40-30}{10}=1 \mathrm{~mL}$
– Le volume du liquide est :
$ \mathrm{V}_{1}=30+7 \times \mathrm{V}_{\mathrm{d}} $
$ \mathrm{~V}_{1}=30+7 \times 1 $
$ \mathrm{~V}_{1}=37 \mathrm{~mL}$
$\star$ Figure 2 :
– Calculons la valeur d’une division :
$\mathrm{V}_{\mathrm{d}}=\frac{45-15}{10}=3 \mathrm{~mL}$
– Le volume du liquide est : $\quad \mathrm{V}_{2}=45+2 \times \mathrm{V}_{\mathrm{d}}$
$ \mathrm{V}_{2}=45+2 \times 3 $
$ \mathrm{~V}_{2}=51 \mathrm{~mL}$
$\star$ Figure 3 :
– Calculons la valeur d’une division :
$V_{d}=\frac{70-45}{5}=5 \mathrm{~mL}$
– Le volume du liquide est : $\quad \mathrm{V}_{3}=45-4 \times \mathrm{V}_{\mathrm{d}}$
$\mathrm{V}_{3}=45-4 \times 5$
$\mathrm{V}_{3}=25 \mathrm{~mL}$
IV – Mesure du volume d’un solide :
Manipulation :
Mesure du volume d’un solide par déplecement d’un liquide
Notons: – $\mathrm{V}_{\mathrm{S}}$ le volume du corps (S).
– $\mathrm{V}_{1}$ : représente le volume du liquide.
– $\mathrm{V}_{2}$ : représente le volume du liquide et du solide ( S ).
Nous écrivons: $\mathrm{V}_{2}=\mathrm{V}_{\mathrm{S}}+\mathrm{V}_{1}$
Donc : $V_{S}=V_{2}-V_{1}$
Application numérique : $\mathrm{V}_{1}=55 \mathrm{~mL}$ et $\mathrm{V}_{2}=85 \mathrm{~mL}$
On a: $\mathrm{V}_{\mathrm{S}}=\mathrm{V}_{2}-\mathrm{V}_{1}$
$\mathrm{V}_{\mathrm{S}}=85 \mathrm{~mL}-55 \mathrm{~mL}$
$\mathrm{V}_{\mathrm{S}}=30 \mathrm{~mL}$
Remarque : Le volume d’un corps ne change pas même si on change sa forme.
Exercice 1:
$1)$ Compléter le tableau suivant :
$\begin{array} {|r|r|}\hline Grandeur \quad physique & Symbole \quad & Unité \quad internationale & Instrument \quad de \quad mesure \\ \hline Le \quad volume & … …………… & … …………… & ……………… \\ \hline \end{array}$
$2)$ Convertir à l’unité demandée
$72 \mathrm{dm}^{3}=………. \mathrm{~cm}^{3}$
$0.2 \mathrm{cL}=………. \mathrm{~cm}^{3}$
$0.5 L=………. \mathrm{dm}^{3}$
$47.8 \mathrm{dm}^{3}=………. \mathrm{dL}$
$20 \mathrm{~mL}=………. \mathrm{~cm}^{3}$
$32 \mathrm{dL}=………. \mathrm{~L}$
$1650 \mathrm{~mL}=………. \mathrm{~L}$
$10 \mathrm{~m}^{3}=………. \mathrm{~L}$
$14 \mathrm{hL}=………. \mathrm{~m}^{3}$
$20 \mathrm{~mL}=………. \mathrm{~cm}^{3}$
$1)$ Compléter le tableau suivant :
$\begin{array} {|r|r|}\hline Grandeur \quad physique & Symbole & Unité \quad internationale & Instrument \quad de \quad mesure \\ \hline Le \quad volume \quad & V & Mètre \quad cube \quad (\mathrm{m}^{3}) & Éprouvette \quad graduée \\ \hline \end{array}$
$2)$
$72 \mathrm{dm}^{3}=72000 \mathrm{~cm}^{3}$
$0.2 \mathrm{cL}=2 \mathrm{~cm}^{3}$
$0.5 L=0.5 \mathrm{dm}^{3}$
$47.8 \mathrm{dm}^{3}=478 \mathrm{dL}$
$20 \mathrm{~mL}=20 \mathrm{~cm}^{3}$
$32 \mathrm{dL}=3.2 \mathrm{~L}$
$1650 \mathrm{~mL}=1.65 \mathrm{~L}$
$10 \mathrm{~m}^{3}=10000 \mathrm{~L}$
$14 \mathrm{hL}=1.4 \mathrm{~m}^{3}$
$20 \mathrm{~mL}=20 \mathrm{~cm}^{3}$
Exercice 2:
Pour mesurer le volume d’un liquide, on utilise l’instrument se dissous :

$1)$ Donner le nom de l’instrument qui contient liquide
$2)$ En quelle unité l’instrument est-elle graduée
$3)$ Quelle est la bonne position de l’œil pour bien lire le volume du liquide
$4)$ Quel est le volume qui correspond chaque division graduée
$5)$ Indiquer le volume du liquide
$1)$ Eprouvette graduée
$2)$ $mL$
$3)$ La position $B$
$4)$ Calculons la valeur d’une division : $V_{d}=\frac{60-40}{5}=4 \mathrm{~mL}$
$5)$ Le volume du liquide : $V = 44 mL$
Exercice 3:
$1)$ Calculer le volume d’un parallélépipède rectangle dont les dimensions sont :La longueur: $\boldsymbol{L}=\mathbf{5 d m}$, la largeur : $\ell=4 \mathrm{~cm}$, la hauteur: $\boldsymbol{h}=5 \mathrm{~cm}$.
$2)$ Un dé à jouer de forme d’un cube, son côté à $\mathbf{2 c m}$. Calculer le volume de ce dé :
$3)$ Calculer le volume d’une sphère de rayon $\boldsymbol{r}=\mathbf{3 c m}$
$1)$ On a: $\quad \mathrm{V}=\mathrm{L} \times \ell \times \mathrm{h}$
Conversion : $5 \mathrm{~dm}=50 \mathrm{~cm}$
Application numérique : $\mathrm{V}=50 \mathrm{~cm} \times 4 \mathrm{~cm} \times 5 \mathrm{~cm}$
Donc: $\mathrm{V}=1000 \mathrm{~cm}^{3}$
$2)$ On a: $\quad \mathrm{V}=\mathrm{a} \times \mathrm{a} \times \mathrm{a}$
Application numérique : $\mathrm{V}=2 \mathrm{~cm} \times 2 \mathrm{~cm} \times 2 \mathrm{~cm}$
Donc: $\mathrm{V}=8 \mathrm{~cm}^{3}$
$3)$ On a: $\quad \mathrm{V}=\frac{4}{3} \times \pi \times \mathrm{R}^{3}$
Application numérique : $\mathrm{V}=\frac{4}{3} \times 3,14 \times \mathrm{3}^{3}$
Donc: $\mathrm{V}=113,1 \mathrm{~cm}^{3}$
Exercice 4:
Comparer les deux volumes suivants : $V_{1}=0,0024 \mathrm{~m};V_{2}=1200 \mathrm{~cL}$.
Quel est le plus grand et combien de fois est-il plus grand.
On sait que : $1 m^{3}=1000 L$, alos : $V_{1}=0.00224 \times 1000 L=2.4 L$
On sait que aussi que $1 c L=0.01 L$ donc : $V_{2}=1200 c L=1200 \times 0.01=12 L$
Par conséquent $V_{2}>V_{1}$.
Pour calculer le nombre de fois, il faut calculer le rapport du grand volume sur le petit volume donc: $\frac{V_{2}}{V_{1}}=\frac{12}{2.4}=5$
Et finalement : $V_{2}$ est 5 fois plus grand que $V_{1}$.
Exercice 5:
Pour mesurer le volume d’un corps solide, on réalise l’expérience suivante : on verse un peu d’eau dans une éprouvette puis on introduit un corps solide dans laquelle. (Voir la figure ci-contre)
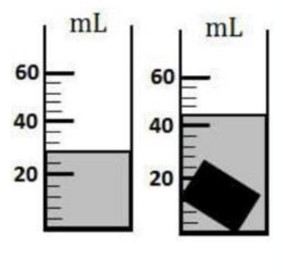
$1)$ Quel est le volume qui correspond chaque division graduée
$2)$ Indiquer le volume d’eau contenue dans l’éprouvette
$3)$ Déduire le volume du corps solide
$1)$ $V_{d}=\frac{60-40}{5}=4 \mathrm{~mL}$
$2)$ Le volume d’eau : $V_{e}=28 \mathrm{~mL}$
$3)$ Le volume du corps solide $V_{s}$
Soit $V_{a}=44 \mathrm{~mL}$ le volume d’eau plus le corps solide.
Alors : $V_{s}=V_{a} – V_{e}=44 \mathrm{~mL} – 28 \mathrm{~mL}$
Donc : $V_{s}= 16 \mathrm{~mL}$
Exercice 6:
Pour mesurer le volume d’une bille, Imane a mis un liquide dans éprouvette graduée en mL. elle introduit en suite 3 billes identiques dans l’éprouvette et mesure le volume totale. Comme le montre la figure.
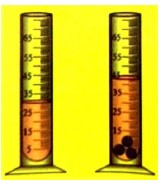
Quel est le volume de chaque bille ?
Le volume du liquide est mesuré par l’éprouvette graduée : $V(\text { liquide })=30 \mathrm{~mL}$
Le volume totale est la somme du volume du liquide est aussi le volume des 3 billes.
Soit donc : $V(\text { total })=V(\text { liquide })+V(3 \text { billes })$
Avec : $V(\text { total })=45 m L$
Alors : $V(3 \text { billes })=V(\text { total })-V(\text { liquide })$
Donc : $V(3 \text { billes })=(45-30) m L=15 m L$
Finalement le volume d’une bille est $V(1$ bille $)=\frac{15}{3}=\mathbf{5 m L}$.
Exercice 7:
On considère une sphère de rayon $\mathrm{R}=1,2 \mathrm{~cm}$
$1)$ Calculer le volume de cette sphère
$2)$ On introduit cette sphère dans une éprouvette gardué Contenant un liquide. (Voir la figure ci-contre)
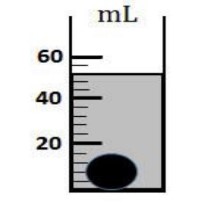
$a)$ Indiquer le volume de l’ensemble $\{ liquide + sphère \}$
$b)$ Déduire le volume du liquide
$1)$ On a: $\quad \mathrm{V_{s}}=\frac{4}{3} \times \pi \times \mathrm{R}^{3}$
Application numérique : $\mathrm{V_{s}}=\frac{4}{3} \times 3,14 \times \mathrm{1,3}^{3}$
Donc: $\mathrm{V_{s}}=7,24 \mathrm{~cm}^{3}$
$2)$
$a)$ le volume de chaque division : $V_{d}=\frac{60-40}{5}=4 \mathrm{~mL}$
Le volume de l’ensemble $ \{ liquide + sphère \}$ : $V_{ls}=52 \mathrm{~mL}$
$b)$ Déduire le volume du liquide :
$V_{l}=V_{ls} – V_{s}=52 \mathrm{~mL} – 7,24 \mathrm{~mL}$
$V_{l}= 44,76 \mathrm{~mL}$
Exercice 8:
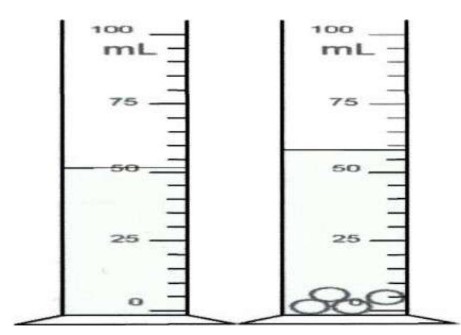
$1)$ Quel est le volume d’une division ?
$2)$ Quel est le volume du liquide ?
$3)$ Quel est le volume du liquide et des $4$ biles?
$4)$ Quel est le volume de $4$ biles ?
$5)$ Quel est le volume d’une seule bile ?
$1)$ Quel est le volume d’une division ?
Le volume de chaque division : $V_{d}=\frac{100-75}{5}=5 \mathrm{~mL}$
$2)$ Quel est le volume du liquide ?
Le volume du liquide : $V_{l}=51 \mathrm{~mL}$
$3)$ Quel est le volume du liquide et des $4$ biles?
Le volume du liquide : $V_{l+4b}=69 \mathrm{~mL}$
$4)$ Quel est le volume de $4$ biles ?
$V_{4b}=V_{l+4b} – V_{l}= 69 \mathrm{~mL} – 51 \mathrm{~mL} =18 \mathrm{~mL}$
$5)$ Quel est le volume d’une seule bile ?
$V_{b}=\frac{V_{4b}}{4}= \frac{18}}{4} =6 \mathrm{~mL}$
Exercice 9:
On considère un château d’eau cylindrique situé en haut d’une montagne. Il permet de distribuer l’eau potable pour les habitations d’un village.

• Les dimensions du château sont :
– Diamètre : $\mathrm{d}=4 \mathrm{~m}$
– Hauteur : $\mathrm{h}=180 \mathrm{~cm}$
– Les données : $\pi=3,14$
$1)$ Calculer le volume de ce château en $\mathrm{m}^{3}$.
$2)$ Le prix d’un mètre- cube est $6 dh$ . Calculer le prix du remplissage.
$1)$ Calculer le volume de ce château en $\mathrm{m}^{3}$.
Les dimensions du château sont :
– Diamètre : $\mathrm{d}=4 \mathrm{~m}$ , donc le rayon $\mathrm{r}=2 \mathrm{~m}$
– Hauteur : $\mathrm{h}=180 \mathrm{~cm}=1,8 \mathrm{~m}$
– Les données : $\pi=3,14$
On a: $\quad \mathrm{V}= \pi \times \mathrm{R}^{2} \times \mathrm{h} $
Application numérique : $\mathrm{V}=3,14 \times \mathrm{2}^{2} \times \mathrm{1,8} $
Donc: $\mathrm{V}=22,06 \mathrm{~m}^{3}$
$2)$ Le prix du remplissage est $22,06 \times 6 dh = 135,6 dh $
Mesure du volume des solides et des liquides exercices corrigés
