La multiplication des nombres relatifs est un concept mathématique fondamental qui permet de combiner deux nombres relatifs pour obtenir un résultat. Les nombres relatifs incluent à la fois les nombres positifs et les nombres négatifs, et la multiplication de ces nombres obéit à certaines règles importantes.

La multiplication et la division des nombres relatifs sont des opérations mathématiques qui permettent de combiner ou de répartir des nombres positifs et négatifs. Voici un résumé des principales règles pour ces opérations :

1. Multiplication 

Règle de signe du produit : Pour trouver le signe du résultat d’une multiplication de plusieurs nombres relatifs, il suffit de compter le nombre de ” – ” :
• si ce nombre est pair, le résultat est positif.
• si ce nombre est impair, le résultat est négatif.

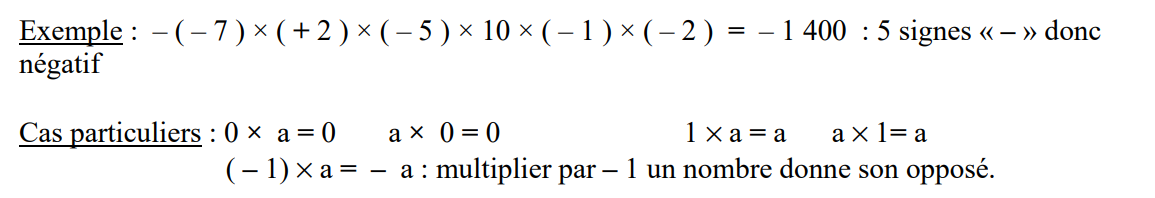
2. Division

Règle de signe de la division : C’est la même que celle de la multiplication.
Conséquence :
Règle des signes généralisée : Pour trouver le signe du résultat d’un calcul qui ne contient
QUE des multiplications et des divisions, on compte le nombre de signes ” – “.
pair : positif impair : négatif

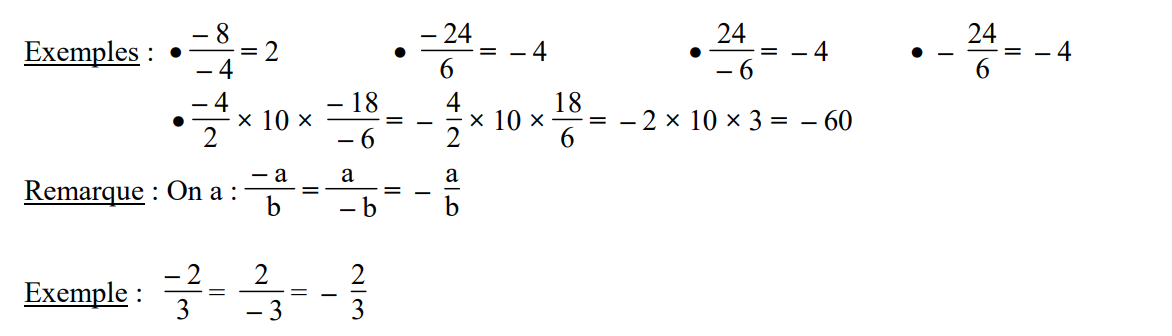
3. Règles de calcul

Règles de priorités de calcul : Pour faire un calcul, on effectue d’abord : les parenthèses

ensuite : les multiplications et les divisions
enfin : les additions et les soustractions.
Quand il y a plusieurs possibilités, on effectue la première dans l’ordre de lecture.

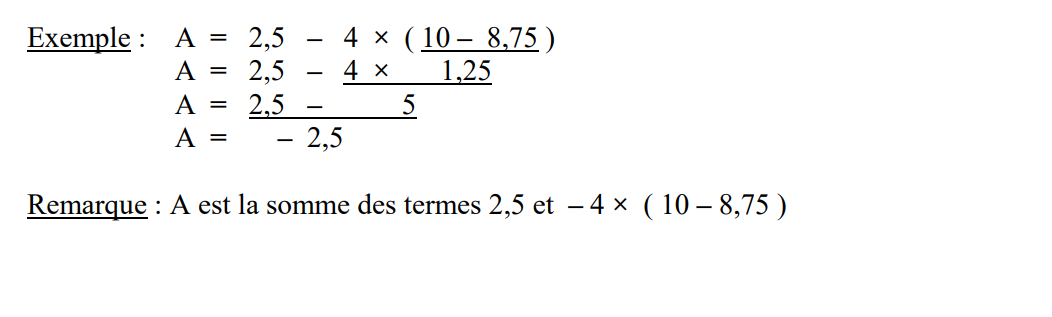
La multiplication et la division des nombres relatifs sont des outils essentiels en mathématiques pour résoudre des problèmes, effectuer des calculs et modéliser des situations où les grandeurs peuvent être positives ou négatives. Elles prennent en compte à la fois les signes et les valeurs absolues des nombres pour déterminer le résultat final.