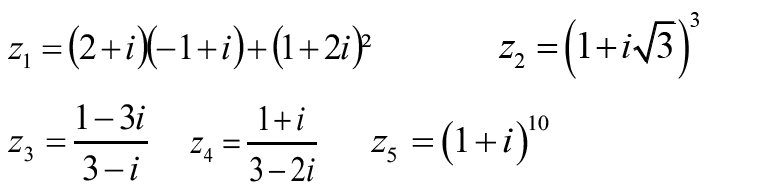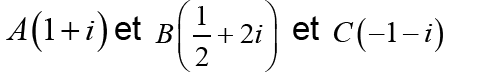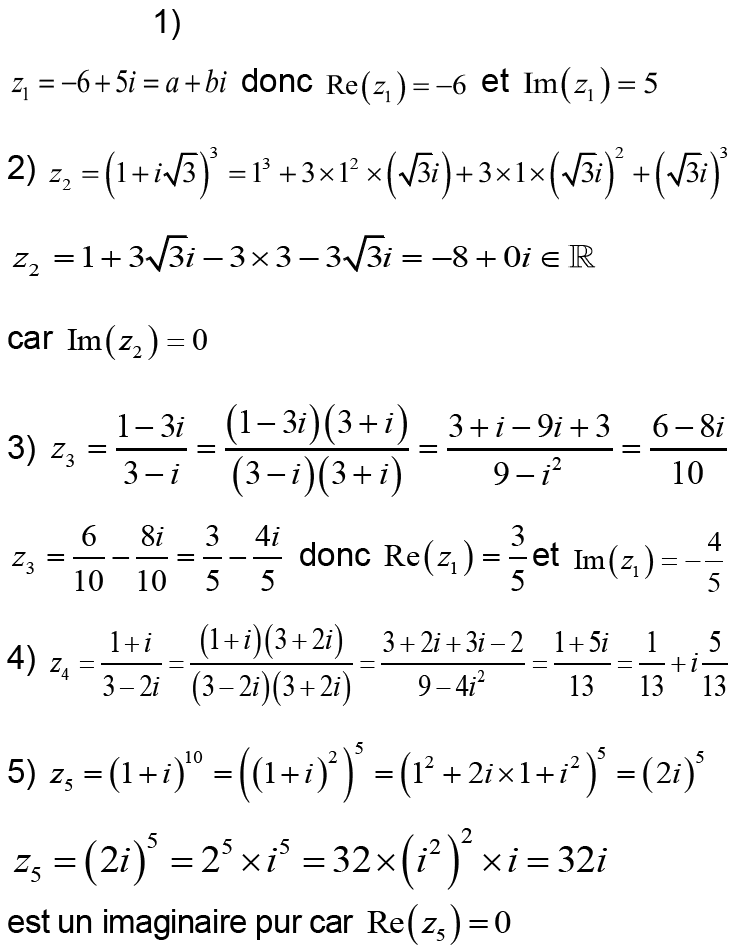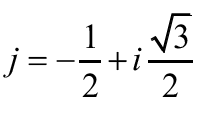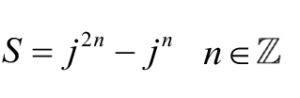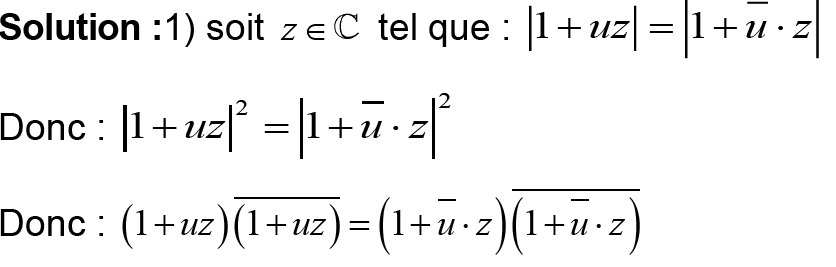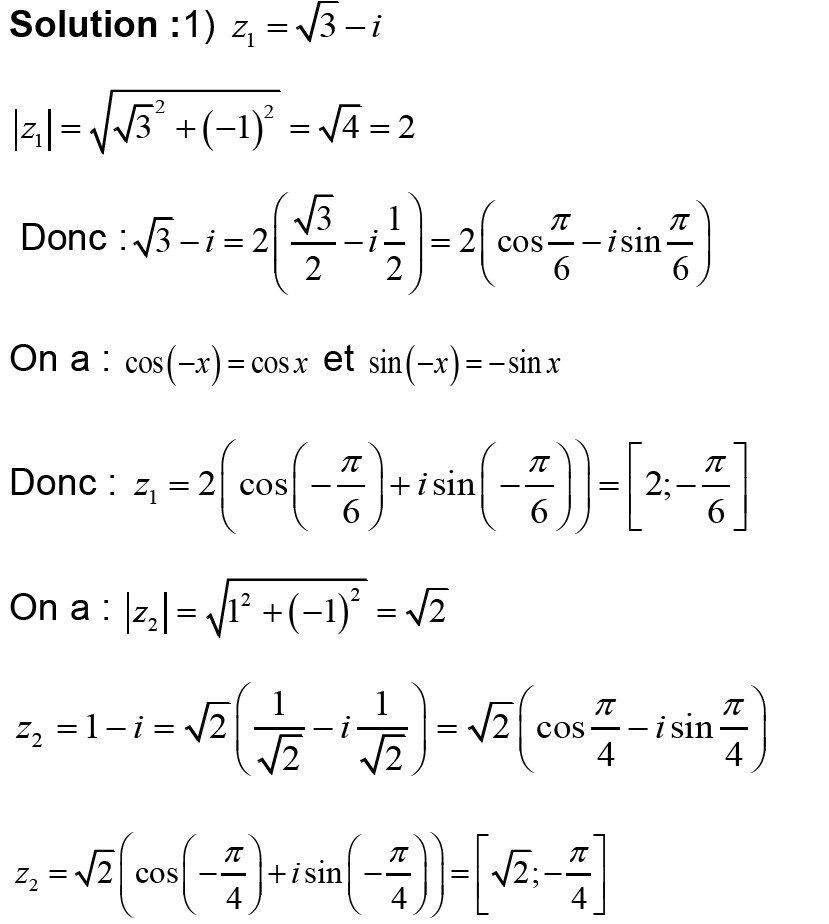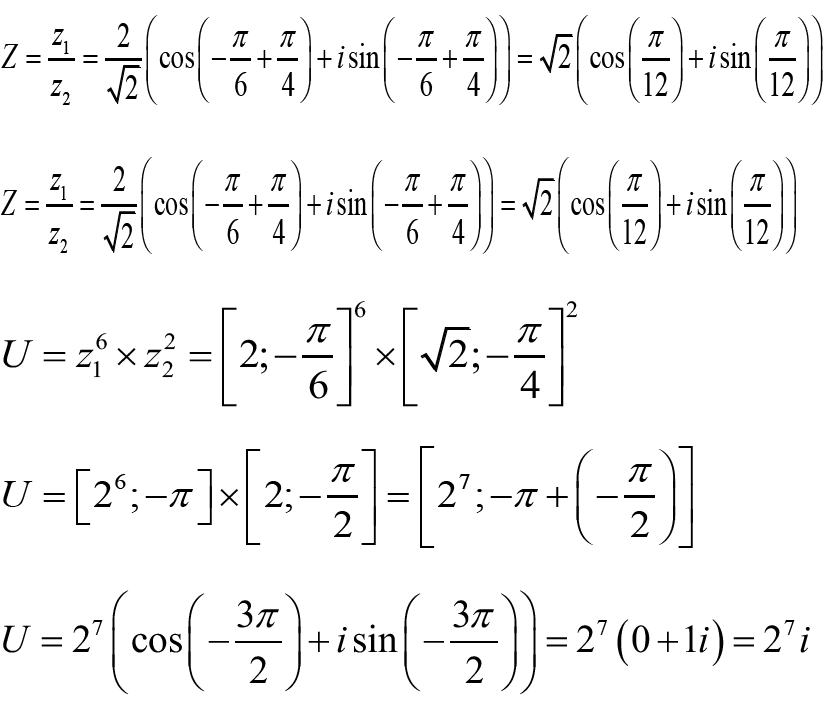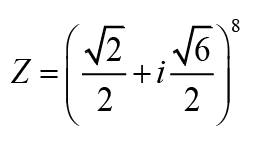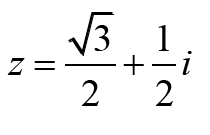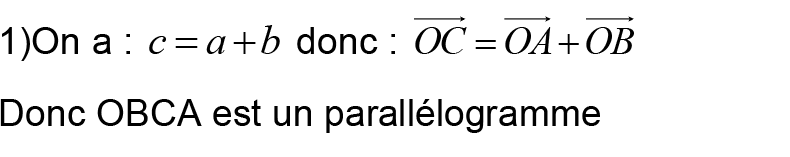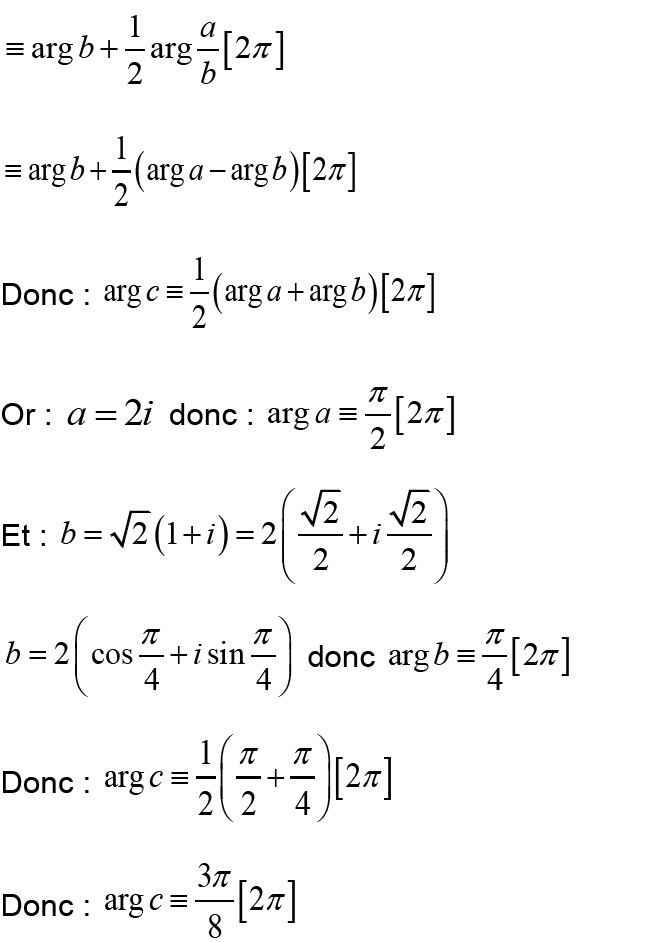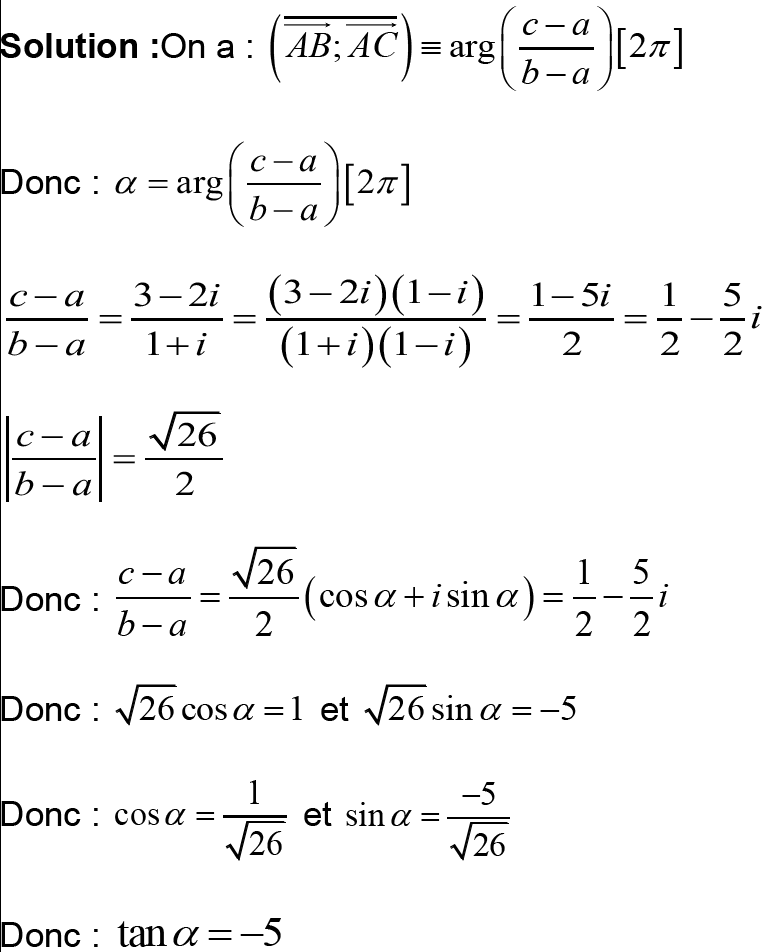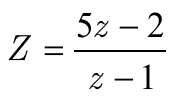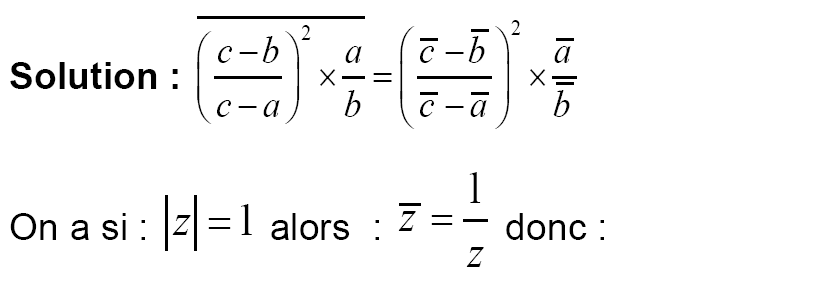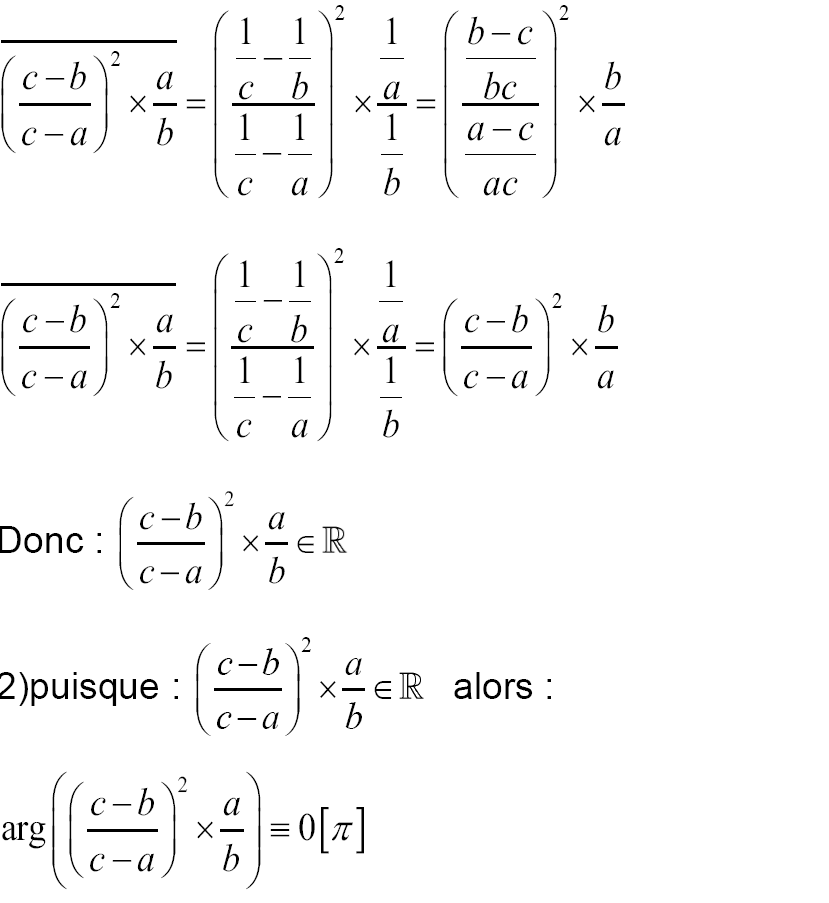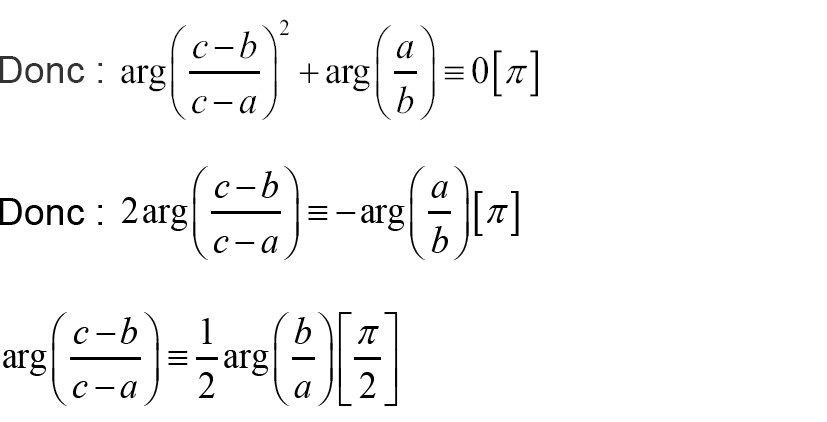Introduction
L’introduction des nombres complexes (partie 1) élargit l’ensemble des nombres réels à un domaine plus vaste, permettant la résolution de problèmes mathématiques auparavant considérés comme insolubles.
Ces nombres complexes (partie 1) sont essentiels dans divers domaines, de l’ingénierie à la physique, et sont utilisés pour modéliser des phénomènes oscillatoires et des circuits électriques complexes
1- Trouver la forme algébrique et déterminer la parties réelles et imaginaires des nombres complexes suivants :
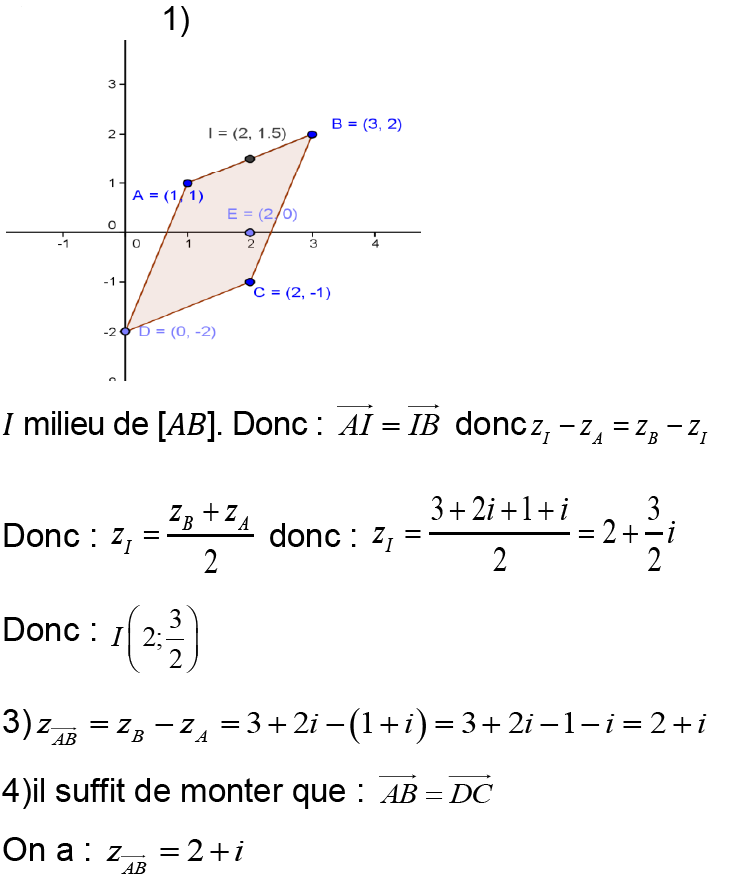
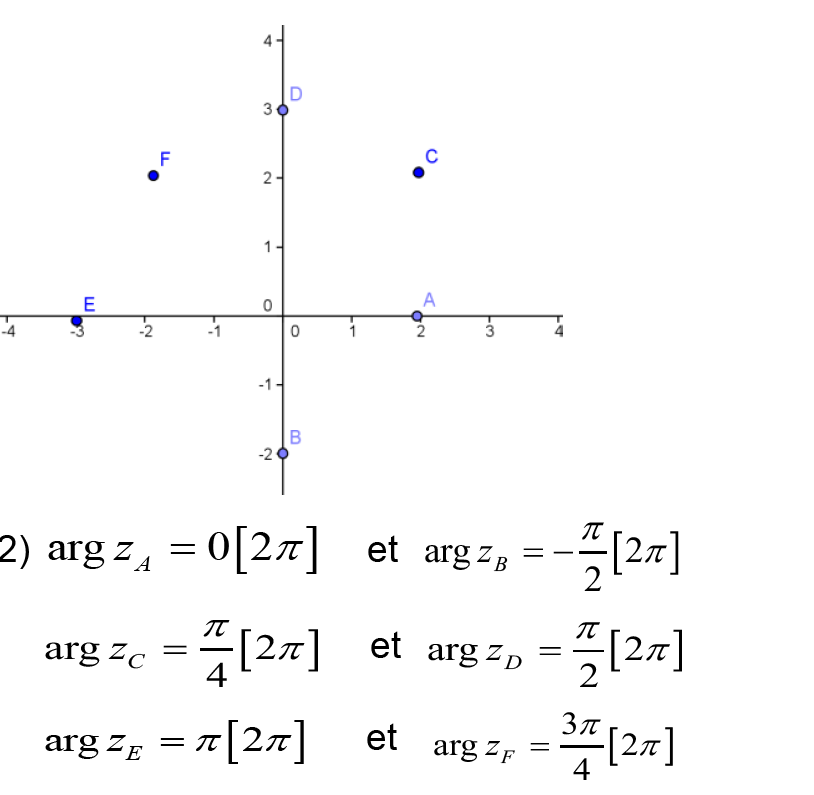
2- soient dans le plan complexe les points :
Montrer que les les points 𝐴, 𝐵 et 𝐶 sont alignés. points :
1- Trouver la forme algébrique et déterminer la parties réelles et imaginaires des nombres complexes suivants :
2- soient dans le plan complexe les points :
Montrer que les points 𝐴, 𝐵 et 𝐶 sont
alignés.
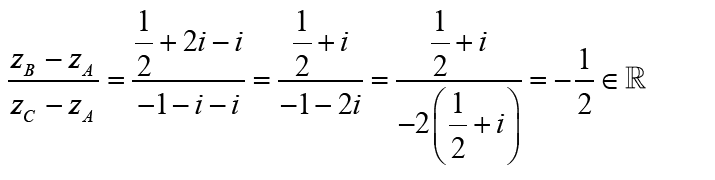
Donc : les les points 𝐴, 𝐵 et 𝐶 sont alignés.
I- Démontrer que S est un nombre réel.
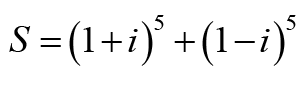
II- on pose :
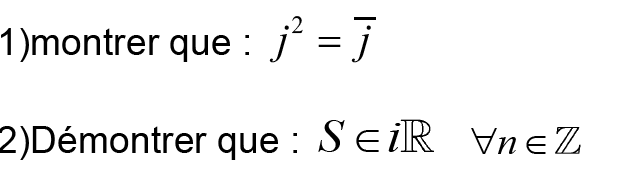
III- soit u ∈ C tel que u ∉ ℜ Montrer que :
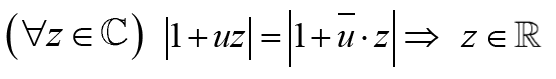
I- 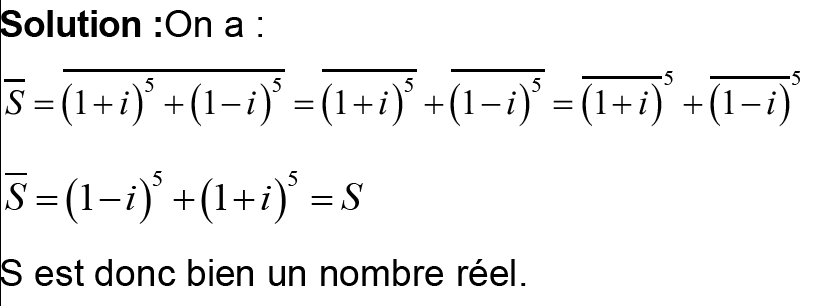
II-
III-
1- Ecrire en fonction de z ¯ le conjugué des nombres complexes suivants :
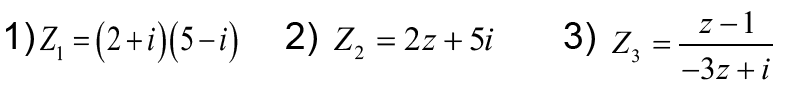
2- Résoudre dans ℂ les équations suivantes :

1- Ecrire en fonction de z ¯ le conjugué des nombres complexes suivants :
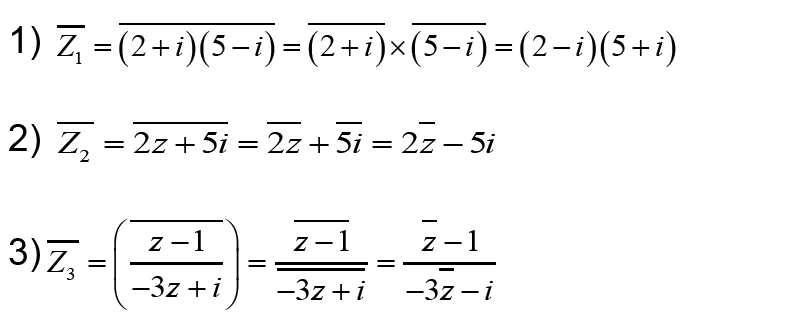
2- Résoudre dans ℂ les équations suivantes :

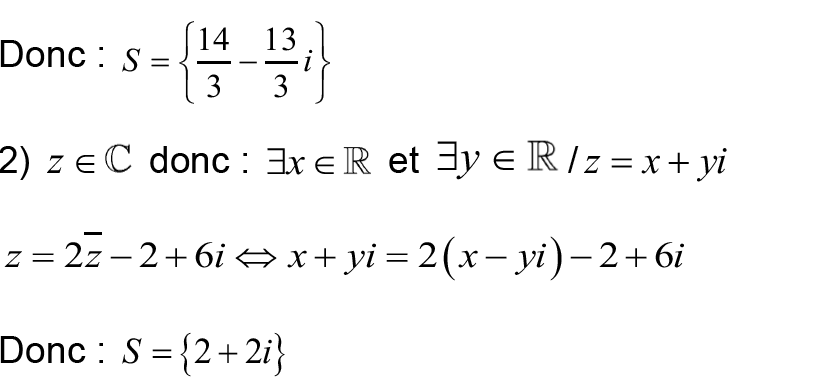
Dans le plan complexe on considère le nombre complexe U et soit M l’image du nombre complexe z et on pose :

Dans le plan complexe on considère le nombre complexe U et soit M l’image du nombre complexe z et on pose :

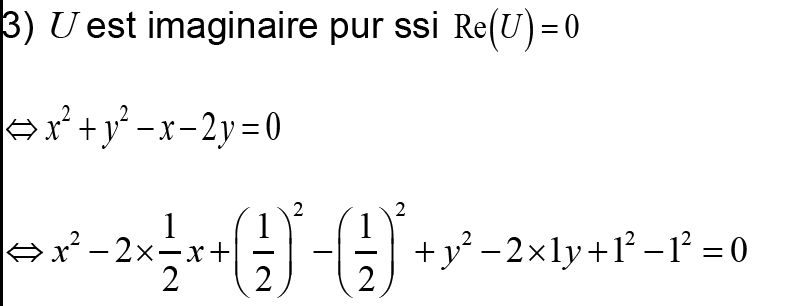

Dans le plan complexe on considère le nombre complexe U et soit M l’image du nombre complexe z et on pose :
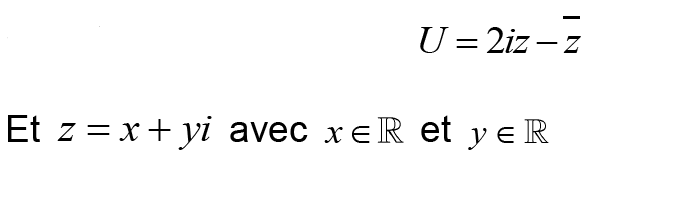

1- Calculer le module des nombres complexes suivants :
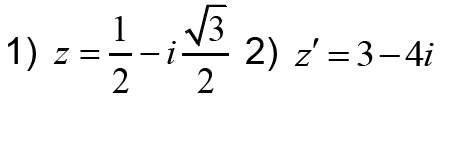
2- Déterminer les modules des complexes suivants :
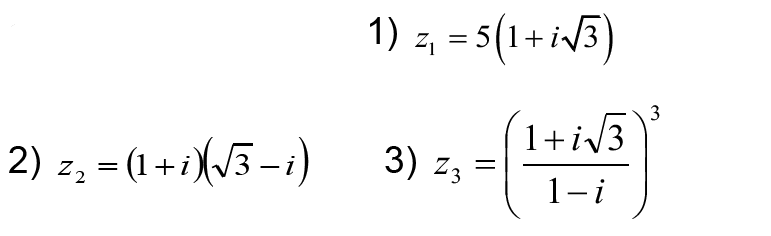
3- Déterminer l’ensemble des points M d’affixe z tels que :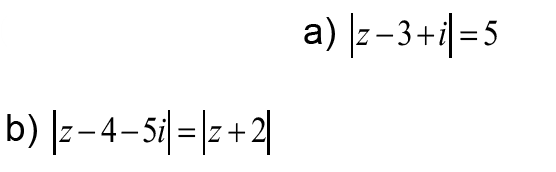
1- Calculer le module des nombres complexes suivants :
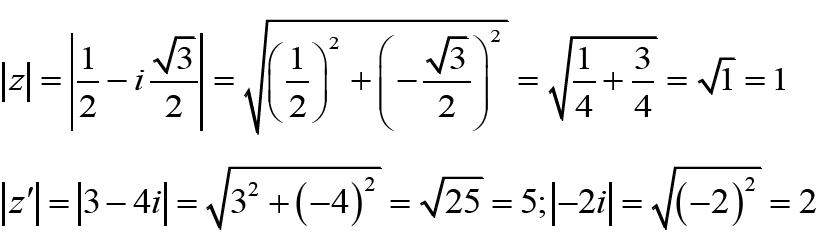
2- Déterminer les modules des complexes suivants :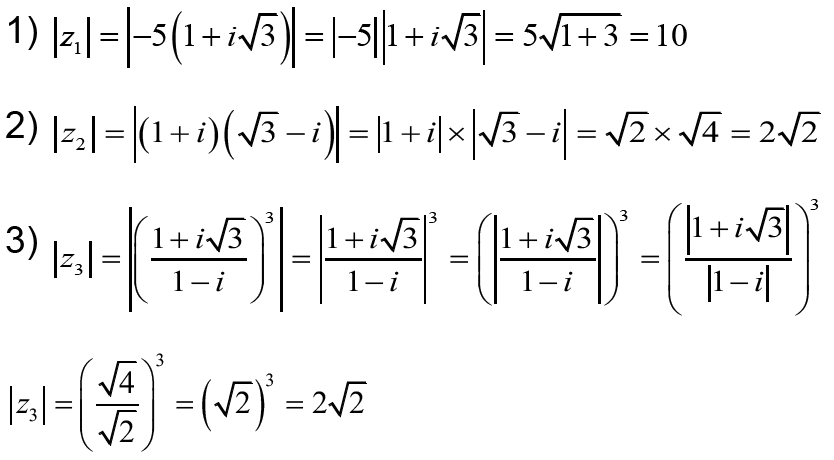
3- Déterminer l’ensemble des points M d’affixe z tels que :
Déterminer l’ensemble des points M d’affixe z tels que :
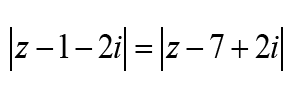
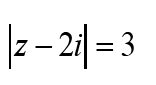
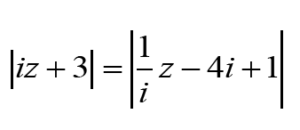
Déterminer l’ensemble des points M d’affixe z tels que :
1- 

2-

3-
I- Donner la forme trigonométrique du nombre complexe 𝑧 dans les cas suivants :
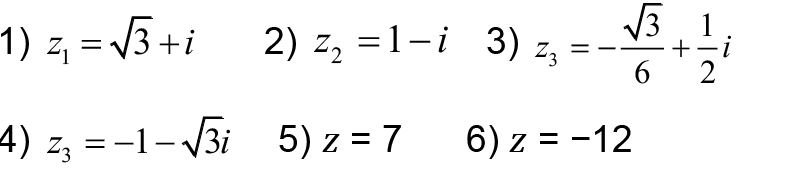
II- Donner la forme trigonométrique du nombre complexe 𝑧 dans les cas suivants avec θ∈]-π , π[ -{0}
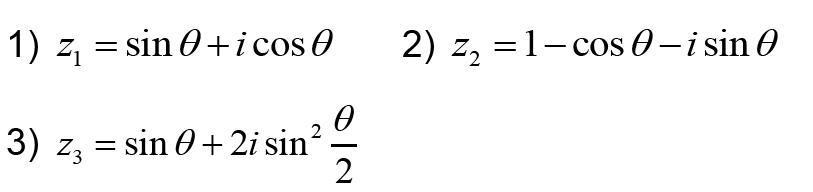
I- Donner la forme trigonométrique du nombre complexe 𝑧 dans les cas suivants :
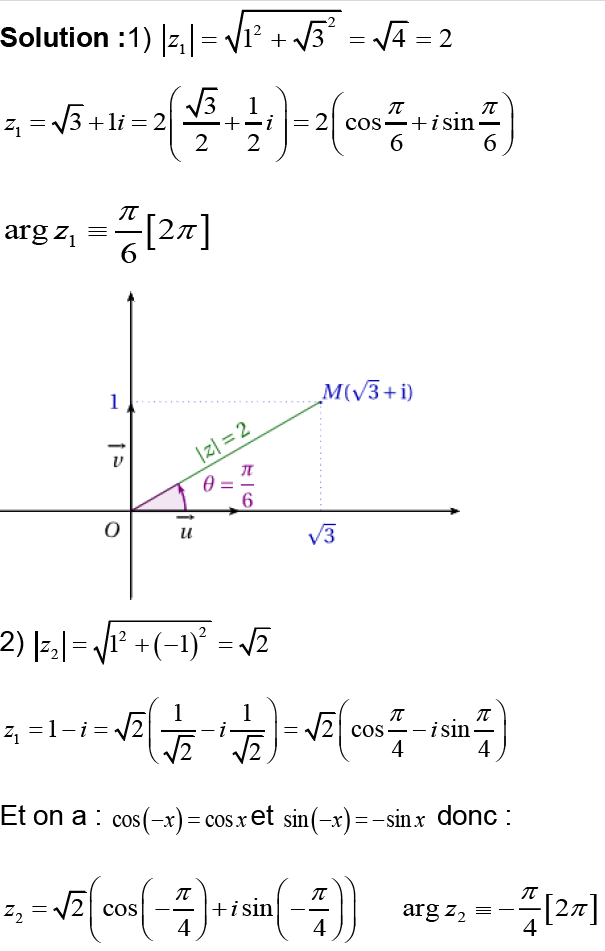
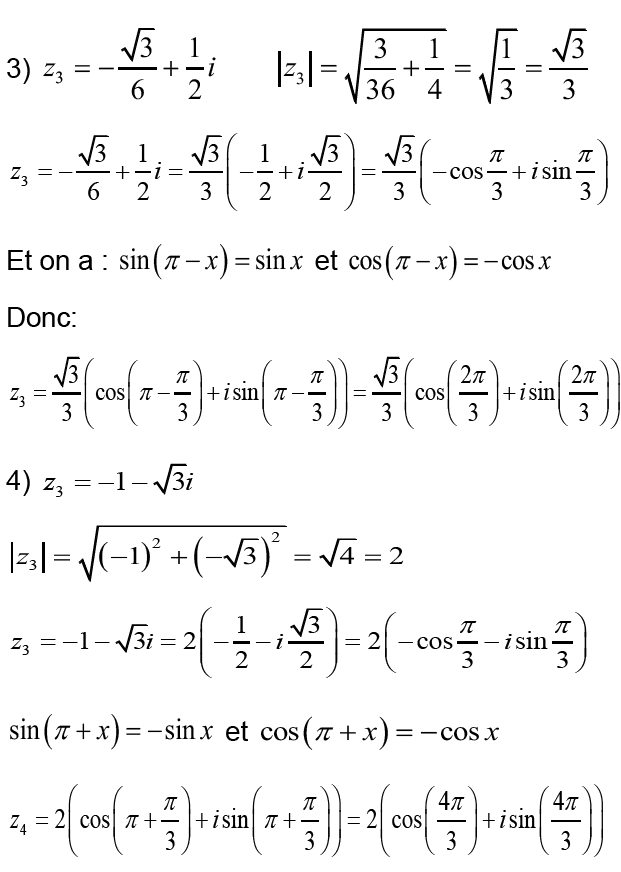
II- Donner la forme trigonométrique du nombre complexe 𝑧 dans les cas suivants avec θ∈]-π , π[ -{0}




1- Ecrire le complexe Z Sous sa forme algébrique
2- Déterminer les racines carrées de Z:
1- Ecrire le complexe Z Sous sa forme algébrique

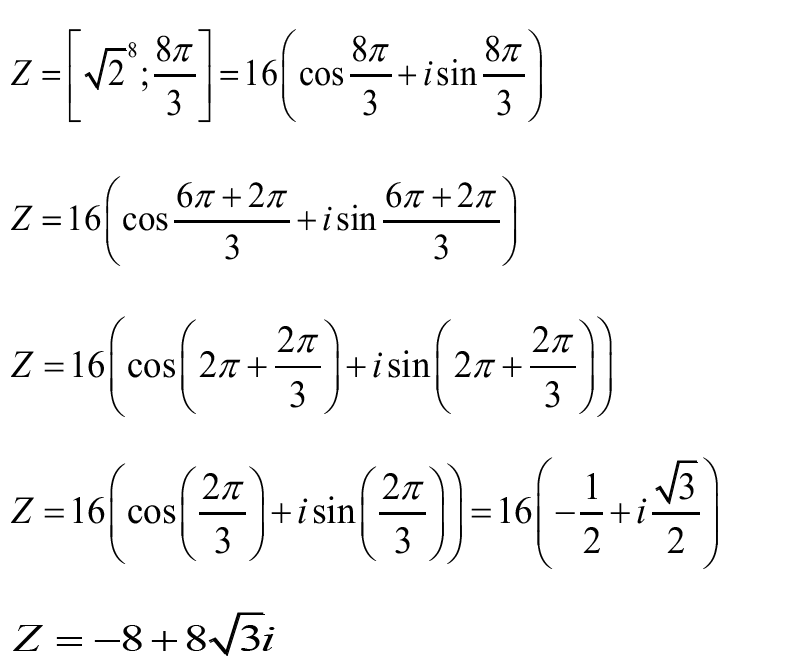
2- Déterminer les racines carrées de Z:
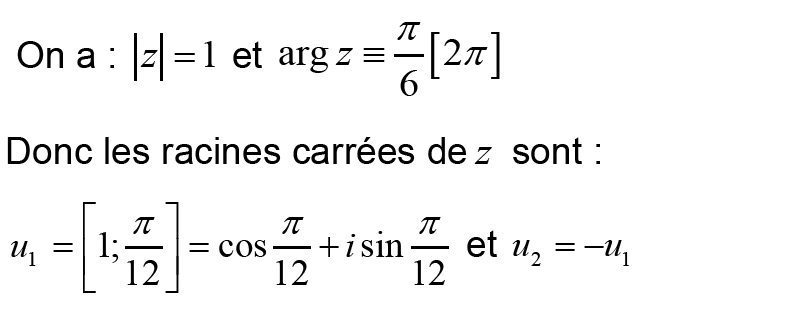
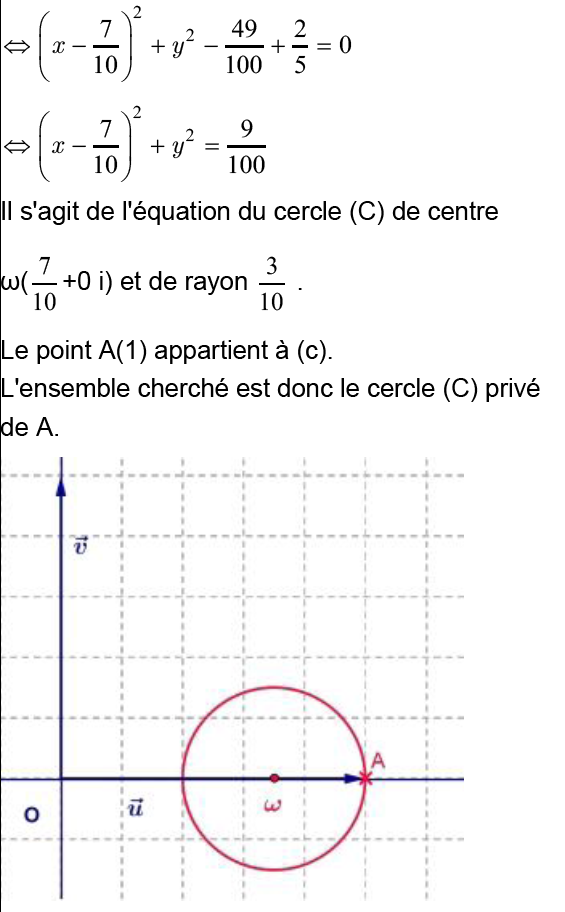
1- Dans le plan complexe, déterminer l’ensemble des points M d’affixe z tel que Z Soit un imaginaire pur.
2- Déterminer l’ensemble des points M d’affixe z tels que :
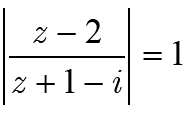
1- Dans le plan complexe, déterminer l’ensemble des points M d’affixe z tel que Z Soit un imaginaire pur.

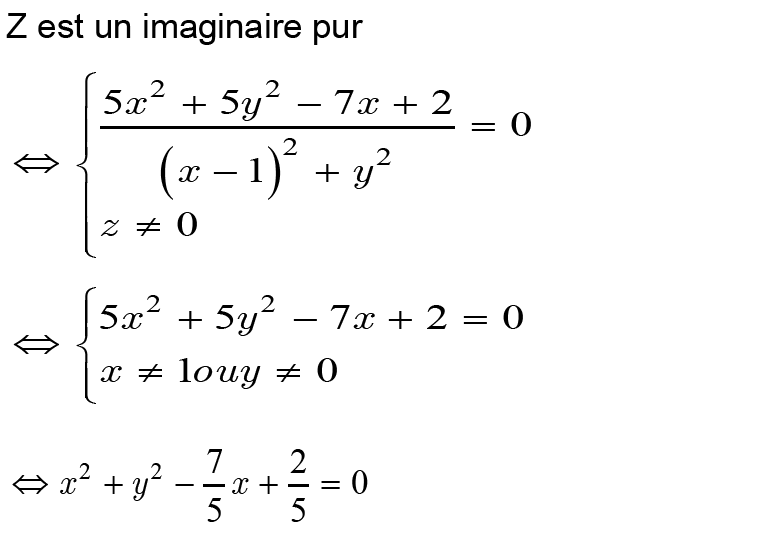
2- Déterminer l’ensemble des points M d’affixe z tels que :