Nombres relatifs : Multiplication et division

Nombres relatifs : Multiplication et division

I- Produit de deux nombres décimaux relatifs

1) Produit de deux nombres décimaux relatifs

Règle ( Règle des signes )

* Le produit de deux nombres relatifs de même signe, est un nombre positif.

* Le produit de deux nombres relatifs signes contraires, est un nombre négatif.

Exemples :

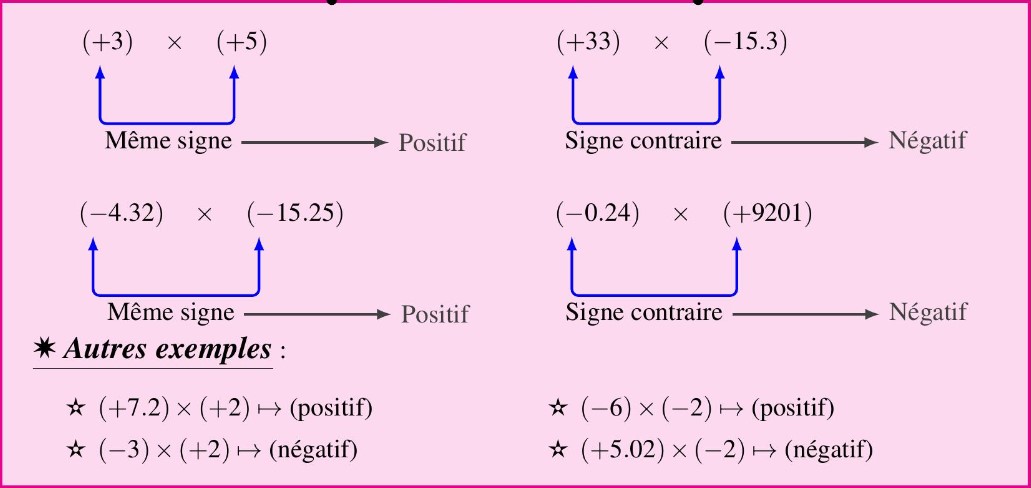
Règle

Pour multiplier deux nombres relatifs

• On détermine le signe du produit avec la règle des signes

• On effectue le produit des distance à zéro

Exemples :

* $(+3) \times(+5)=+15$

* $(+7) \times(+2)=+14$

* $(-6.1) \times(-2)=+12.2$

* $(-4) \times(-4)=+16$

* $(-3) \times(+2)=-6$

* $(+5.5) \times(-2.3)=-12.65$

* $(+13) \times(-4)=-52$

* $(-10) \times(+12)=-120$

Remarque

On peut supprimer le signe ‘ $\times$ ‘ devant un nombre relatif désigné par une lettre ( $a$ par exemple).

Par ailleurs, $a \times b$ s’écrit : $a b$ et $a \times 9$ s’écrit de préfférence : $9 a$

On écrit aussi $-5 x$ au lieu d’écrire : $(-5) \times x$ ou $5 \times(-x)$

* Cas particulier : Pour tout nombre relatifs $a$ :

$1 \times a=a \times 1=a$

$(-1) \times a=a \times(-1)=-a$

$0 \times a=a \times 0=0$

2) Produit de plusieurs nombres relatifs

Règle

$\star$ Le produit de plusieurs nombres relatifs est positif s’il comporte un nombre pair de facteurs négatifs.

$\star$ Le produit de plusieurs nombres relatifs est négatif s’il comporte un nombre impair de facteurs négatifs.

Exemples :

$\star: A=(-5) \times(-2) \times(+1) \times(-4)$

On a le produit $A$ comporte 3 facteurs négatifs et 3 est nombre impair, donc $A$ est négatif

$\star: B=(-3) \times(+6) \times(+7) \times(-2) \times(-9) \times(-5)$

On a le produit $B$ comporte 4 facteurs négatifs et 4 est nombre pair, donc $A$ est positif

Exemple :

Pratiquement :

Calculons: $(-20) \times(-3) \times(+13) \times(+6) \times(+8) \times(-5)$

(1) On détermine le signe du produit :

Il y a 3 ( nombre ompair ) facteurs négatif, donc, le produit est négatif

(2) On multiplie les distance à zéro :

$20 \times 3 \times 13 \times 6 \times 8 \times 5=60 \times 78 \times 40=60 \times 40 \times 78=2400 \times 78=187200$

(3) conclusion du produit :

$(-20) \times(-3) \times(+13) \times(+6) \times(+8) \times(-5)=(-187200)$

II- Quotient de deux nombres relatifs

1) Quotient de deux nombres

Définition

Soient $a$ et $b$ deux nombres décimaux relatifs tel que $b \neq 0$

Le nombre décimal relatif $c$ qui vérifie : $a=b \times c$ s’appelle le quotient de $a$ par $b$

Et on écrit : $\frac{a}{b}=c$ ou $a \div b=c$ ou encore (moins utilisé) $a: b=c$

Exemples :

$ (-10) \div 5=\frac{-10}{5}=(-2), \mathrm{car}-10=5 \times(-2) $

$ (-21) \div(-7)=\frac{-21}{-7}=3, \mathrm{car}-21=(-7) \times 3 $

$ 63 \div(-7)=\frac{63}{-7}=9, \mathrm{car}-10=5 \times(-2)$

Quotient particuliers :

Soit $a$ un nombre décimal relatif non nul

$\left.\frac{a}{1}=a \quad ;  \quad \frac{a}{a}=1 \quad  ;  \quad \frac{0}{a}=0 \quad  ; \quad \frac{a}{0} \text { (n’a pas de sens }\right)$

2) Signe d’un quotient

Règle (Règle des signes )

Soient $a$ et $b$ deux nombre décimaux relatif

$\star$ Si $a$ et $b$ sont de même signe, alors $\frac{a}{b}$ est positif

$\star$ Si $a$ et $b$ sont de signes contraires, alors $\frac{a}{b}$ est négatif

Exemples :

* $\frac{-10}{7}=-\frac{10}{7} $

*$ \frac{-35}{-11}=\frac{35}{11}$

*$ \frac{111}{-37}=\frac{-111}{37}=-\frac{111}{37}$

Remarque

Soient $a$ et $b$ deux nombres décimaux relatifs tel que $b \neq 0$

$\frac{a}{-b}=\frac{-a}{b}=-\frac{a}{b}$

3) Division de deux nombres relatifs

Règle

Pour diviser deux nombres relatifs non nuls, on divise les distances à zéro et on applique la règle des signes

Exemples :

* $A=(-60) \div(-5)=+15$

* $B=(-30) \div(+4)=(-7.5)$

* $C=(+100) \div(+20)=+5$

* $D=(+55) \div(-11)=(-5)$

4) Valeur approchée d’un quotient

Exemples :

On veut calculer le quotient de $13 $ par $-7$, ce quotient est négatif

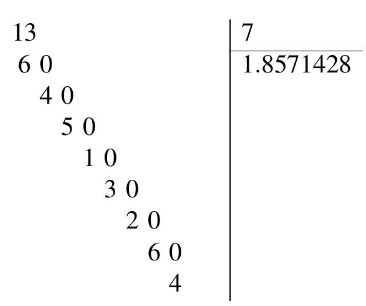
• -1.9 est une valeur approchée au dixième par défaut de $\frac{13}{-7}$

• -1.8 est une valeur approchée au dixième par excès de $\frac{13}{-7}$

• $-1.9<\frac{13}{-7}<-1.8$ est un encadrement au dixième de $\frac{13}{-7}$

Application

Calculer :

* $A=45 \div(-5)$

* $B=(-56) \div(-8)$

* $C=(-59) \div(10)$

* $D=\frac{10}{(-2)}$

* $E=\frac{(-60)}{(-4)}$

* $F=\frac{(+5)}{(+2)}$

Solution

*$ A=45 \div(-5)=-9$

* $B=(-56) \div(-8)=7 $

* $C=(-59) \div(10)= -5.9$

* $D=\frac{10}{(-2)}=-5 $

* $E=\frac{(-60)}{(-4)}=15 $

* $F=\frac{(+5)}{(+2)}=2.5$