Parallélogramme et quadrilatères particuliers
Exercice 1:
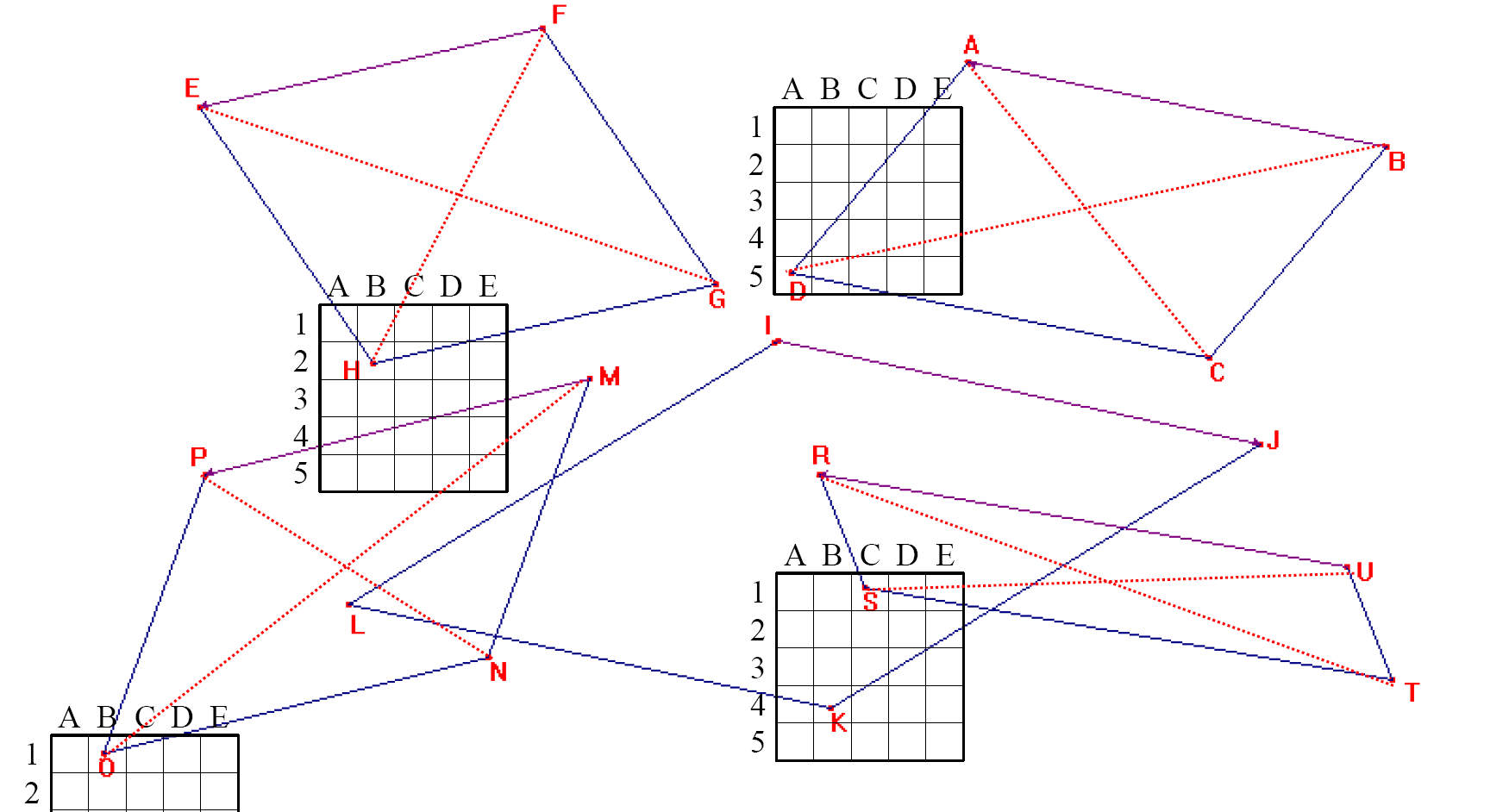
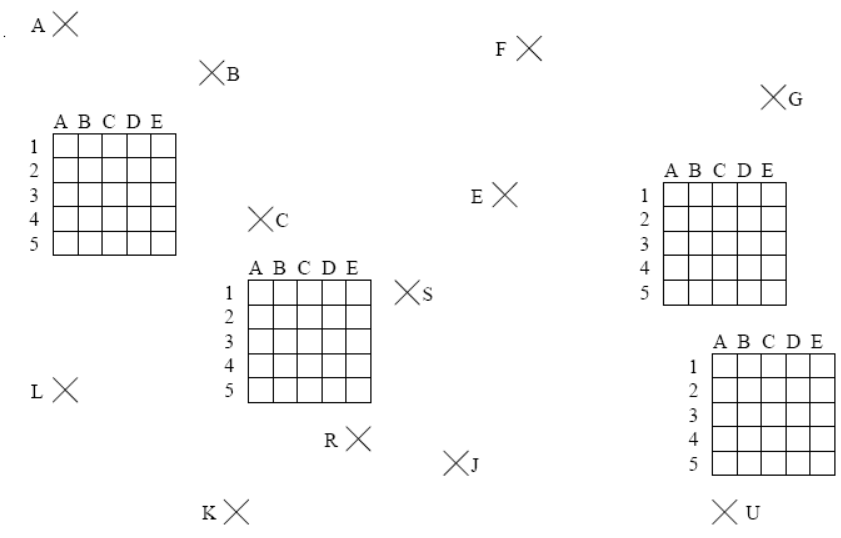
Tracer à la règle et l’équerre les ces parallélogrammes : $ABCD $ ; $EFGH$ ; $IJKL$ ; $RSTU$
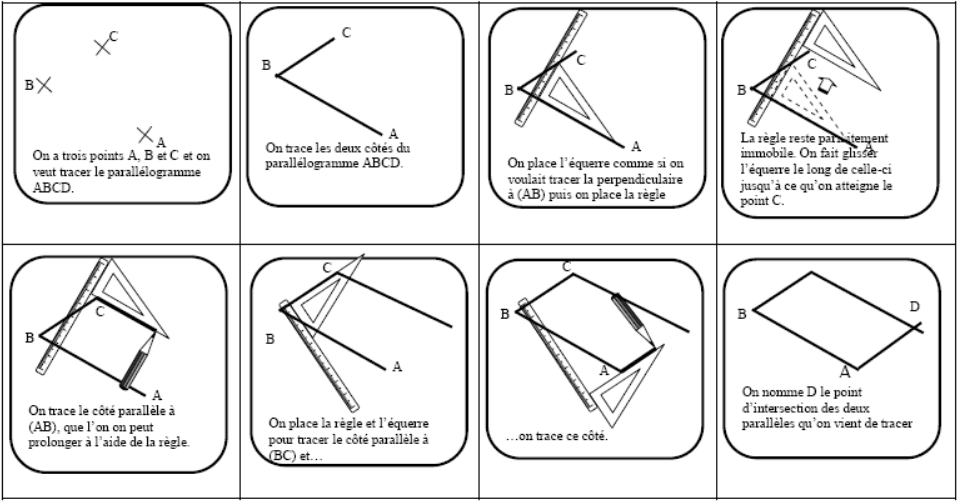
Méthode
Exercice 2:
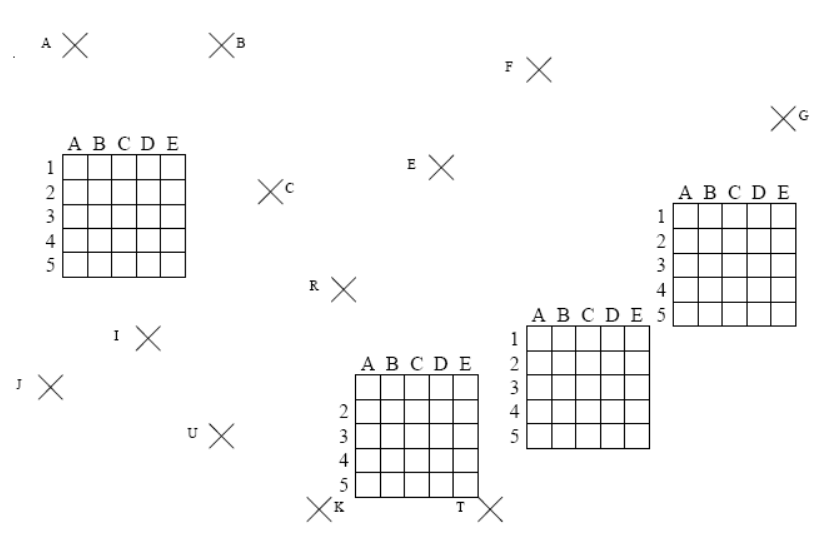
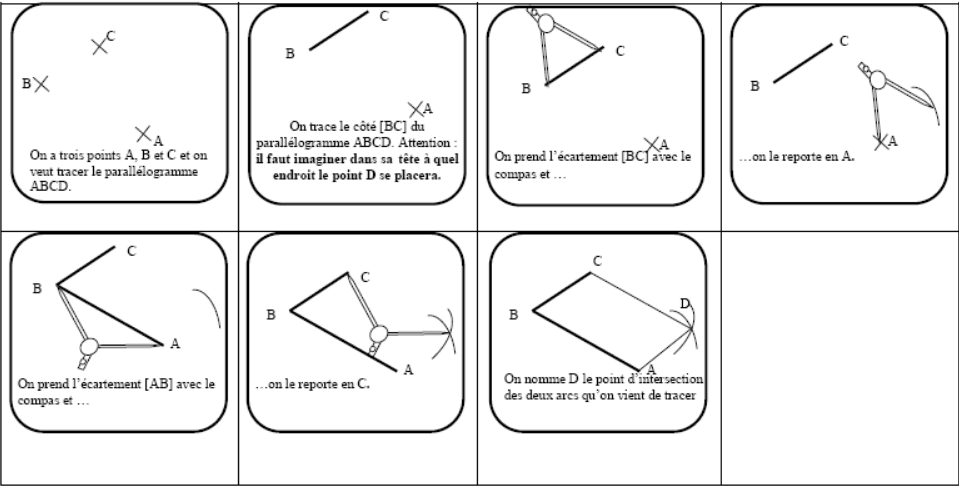
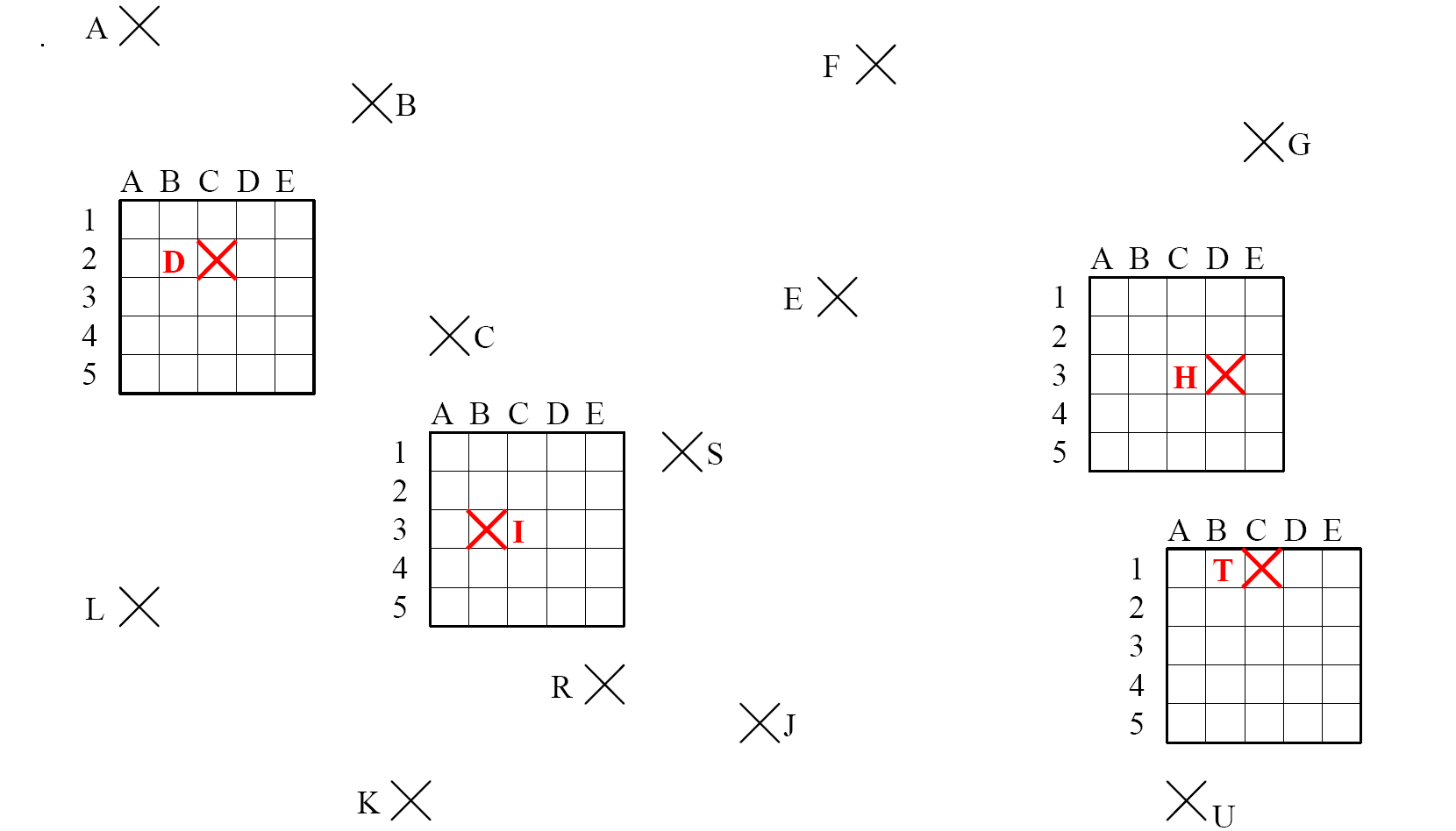
Tracer à l’aide du compas les ces parallélogrammes : $ABCD $ ; $EFGH$ ; $IJKL$ ; $RSTU$
Méthode
Exercice 3:
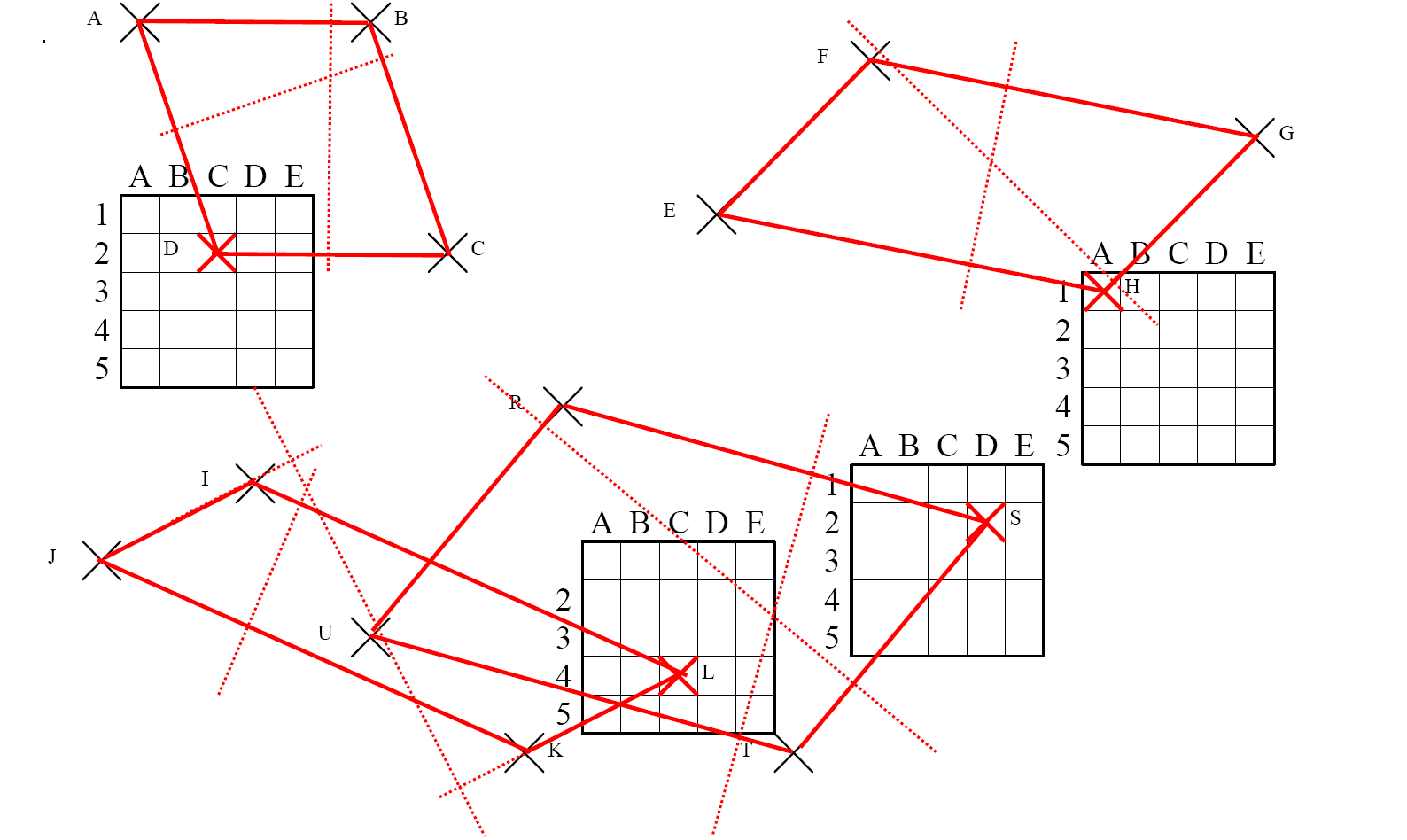
Tracer à l’aide des diagonales les ces parallélogrammes : $ABCD $ ; $EFGH$ ; $IJKL$ ; $RSTU$
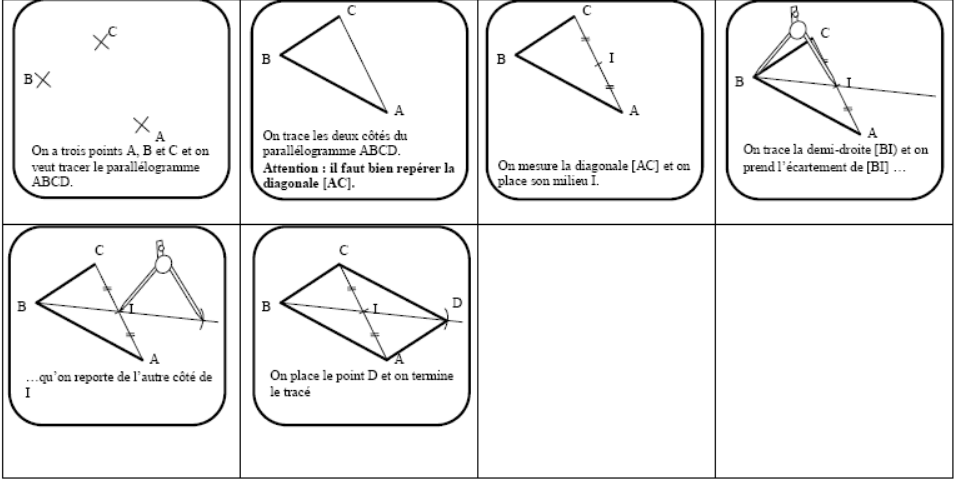
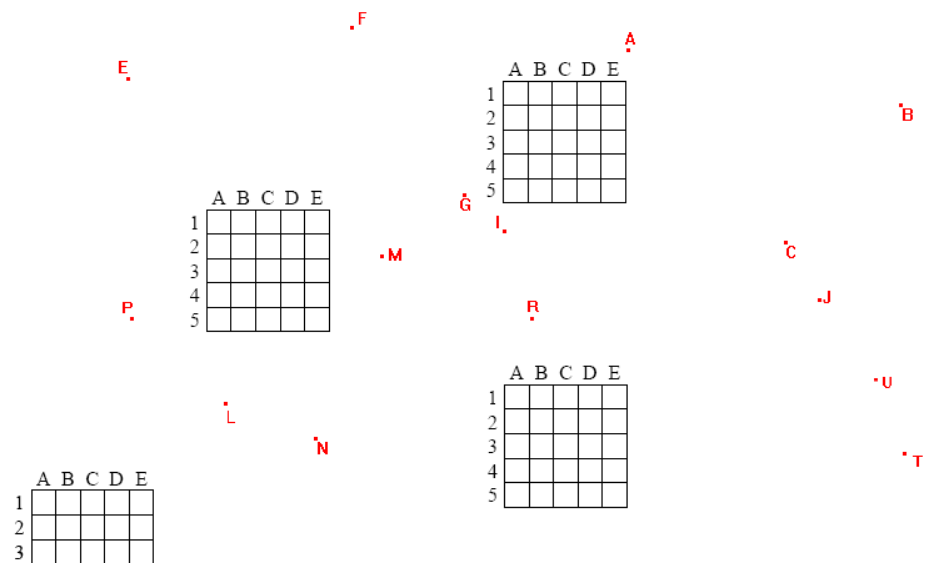
Exercice 4:
Trouver l’emplacement exact du centre de symétrie des figures suivantes (s’il y en a un) :
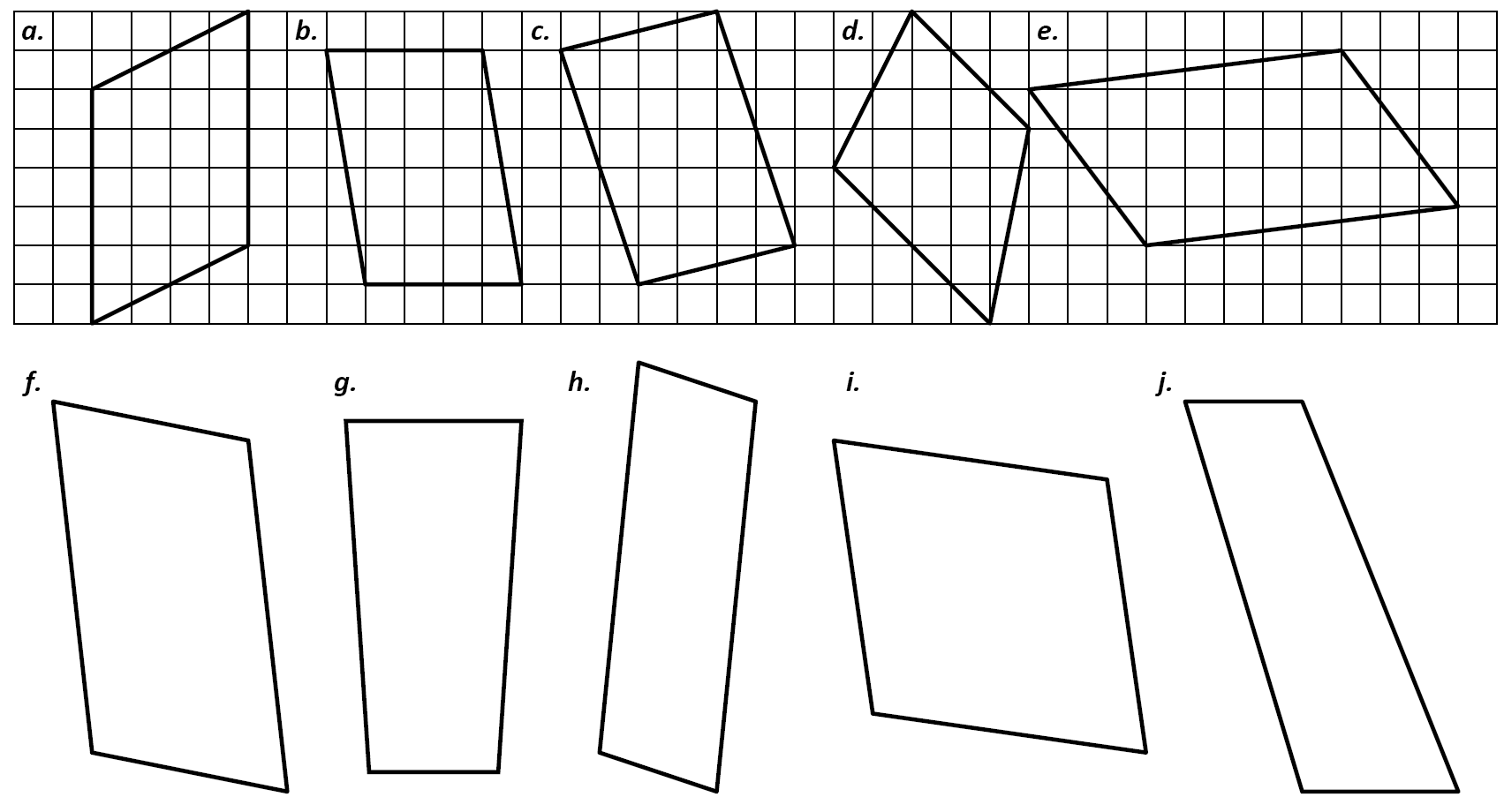
Exercice 5:
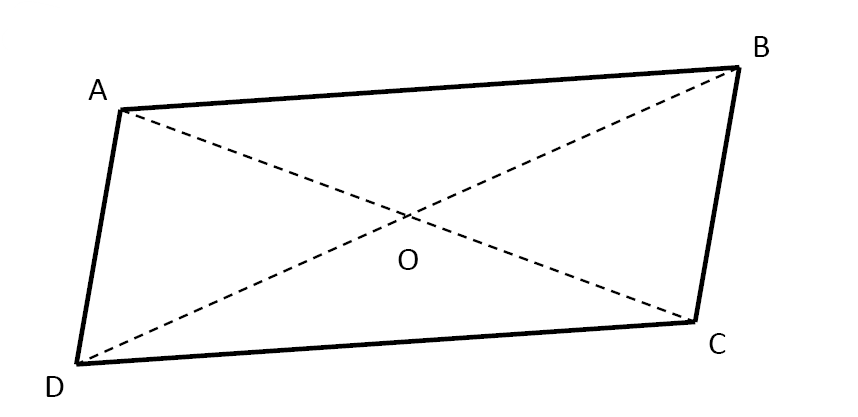
$1)$ Le quadrilatère $ABCD$ est un parallélogramme.
Coder sur cette figure les segments de même longueur.
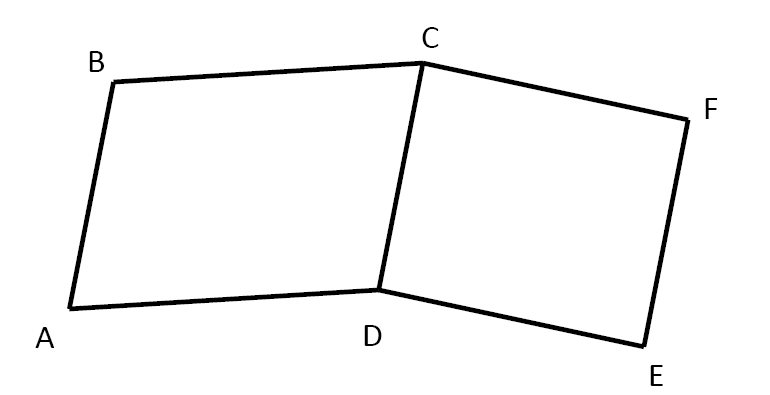
$2)$ $ABCD$ et $CDEF$ sont deux parallélogrammes.
Coder sur cette figure les angles égaux.
$3)$ Construire, en utilisant uniquement la règle, les symétriques $M’$ et $N’$ de $M$ et $N$ par rapport à $O$.
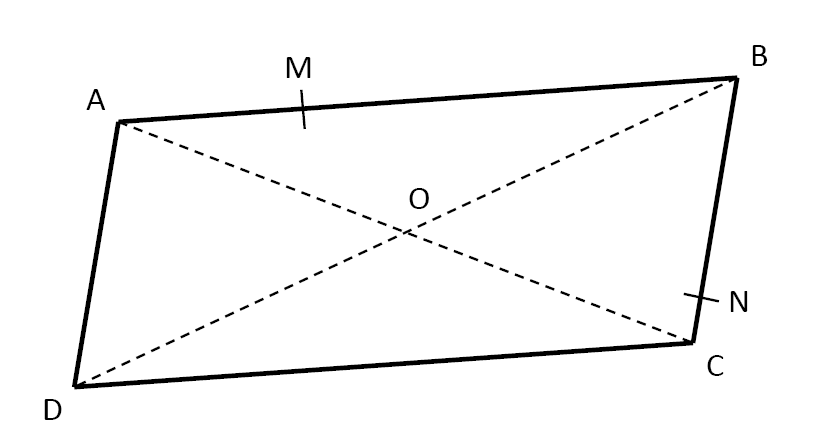
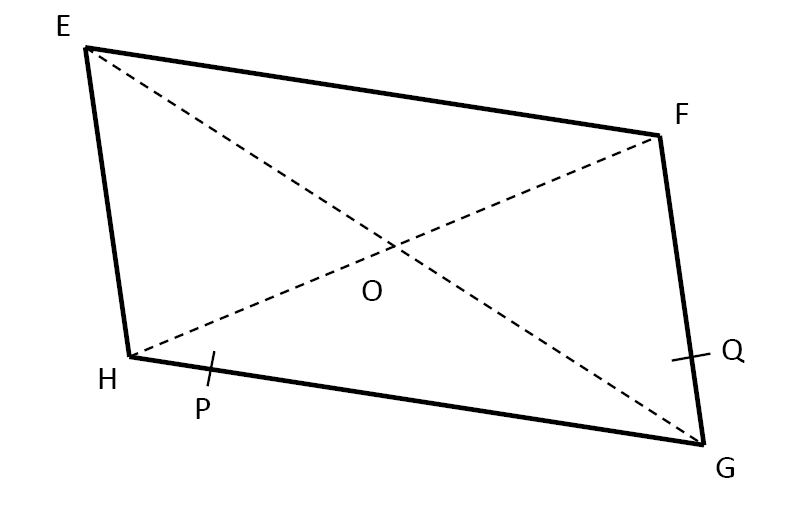
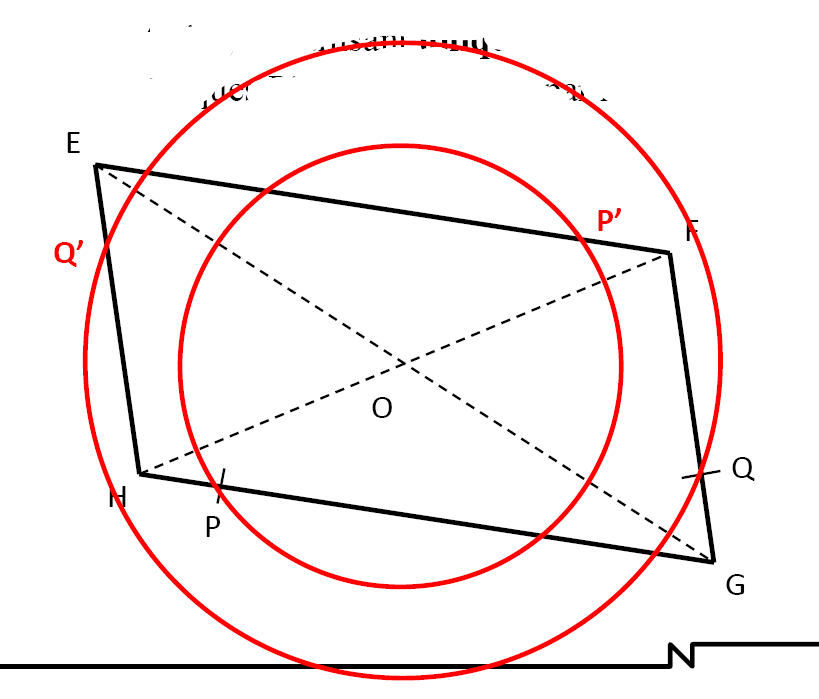
$4)$ Construire, en utilisant uniquement le compas, les symétriques $P’$ et $Q’$ de $P$ et $Q$ par rapport à $O$.
$1)$ 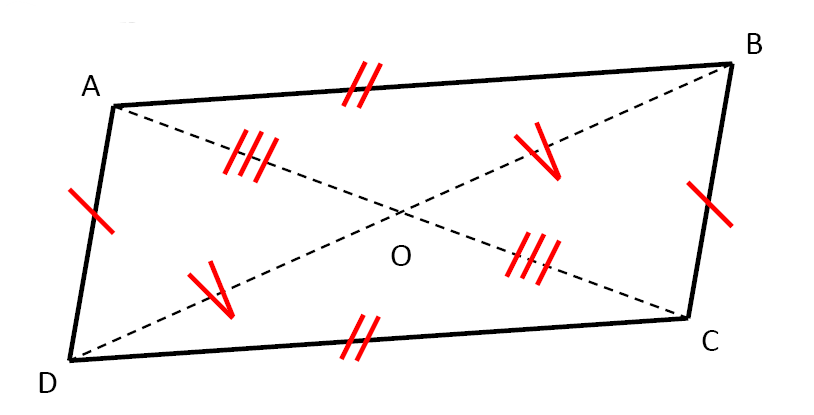
$2)$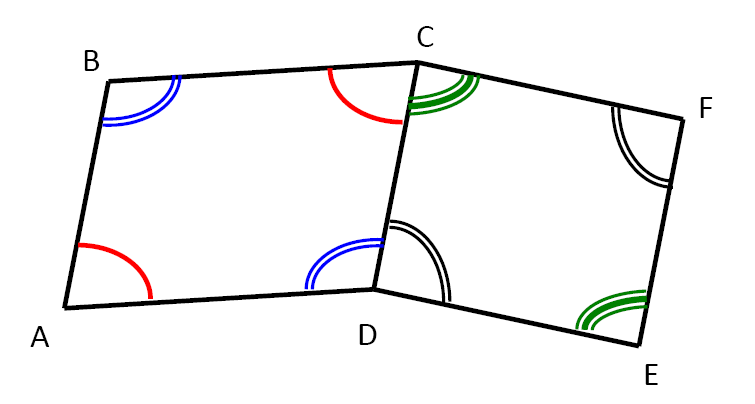
$3)$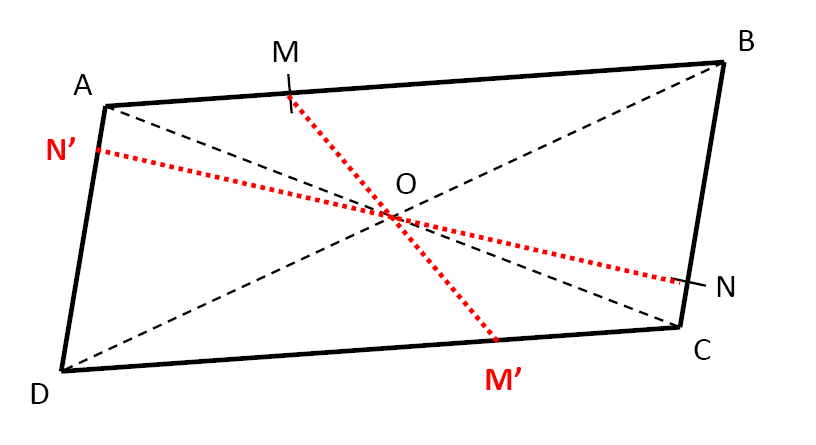
$4)$
Exercice 6:
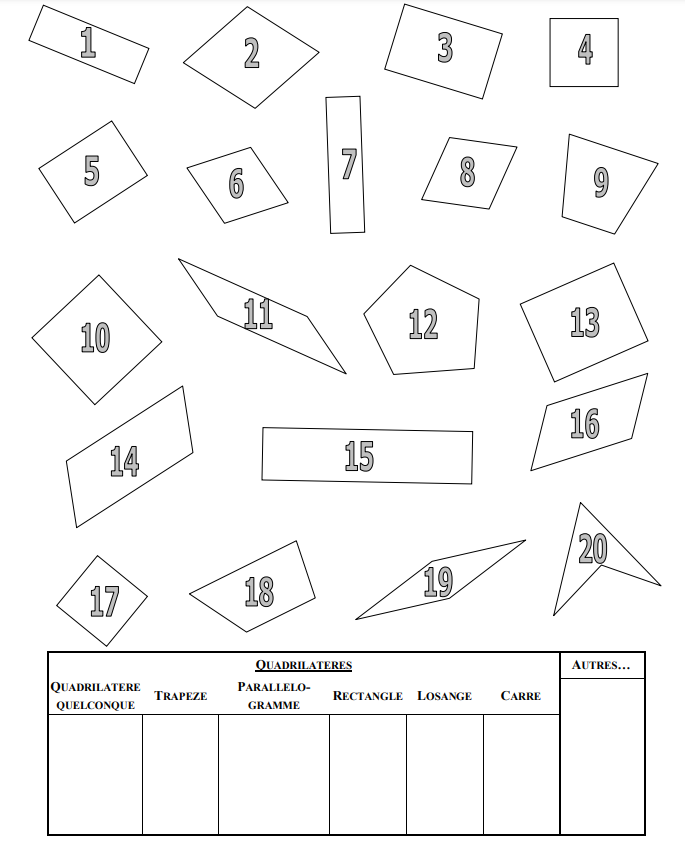
Reconnaître les quadrilatères suivants puis les classer dans le tableau :
Exercice 7:
Compléter les pointillés par les mots :
quadrilatère- quelconque- rectangle -losange- carré -trapèze- parallélogramme- carré
a. Un quadrilatère qui a 4 angles droits est un …………………………………………………..
b. Un quadrilatère qui a 2 côtés égaux est un …………………………………………………..
c. Un quadrilatère qui a 3 angles droits est un …………………………………………………..
d. Un quadrilatère qui a ses côtés opposés parallèles 2 à 2 est un ……………………………………………….
e. Un quadrilatère qui a 2 angles droits et 2 côtés égaux est un …………………………………………………..
f. Un quadrilatère qui a 4 côtés égaux est un …………………………………………………..
g. Un quadrilatère qui a 2 angles droits est un …………………………………………………..
h. Un quadrilatère qui a 2 côtés opposés parallèles est un …………………………………………………..
i. Un quadrilatère qui a 4 angles droits et 4 côtés égaux est un …………………………………………………..
j. Un quadrilatère qui a 3 côtés égaux et 2 côtés opposés parallèles est un ……………..………………………
a. Un quadrilatère qui a 4 angles droits est un rectangle
b. Un quadrilatère qui a 2 côtés égaux est un quadrilatère quelconque
c. Un quadrilatère qui a 3 angles droits est un rectangle
d. Un quadrilatère qui a ses côtés opposés parallèles 2 à 2 est un parallélogramme
e. Un quadrilatère qui a 2 angles droits et 2 côtés égaux est un quadrilatère quelconque
f. Un quadrilatère qui a 4 côtés égaux est un losange
g. Un quadrilatère qui a 2 angles droits est un quadrilatère quelconque
h. Un quadrilatère qui a 2 côtés opposés parallèles est un trapèze
i. Un quadrilatère qui a 4 angles droits et 4 côtés égaux est un carré
j. Un quadrilatère qui a 3 côtés égaux et 2 côtés opposés parallèles est un trapèze
Exercice 8:
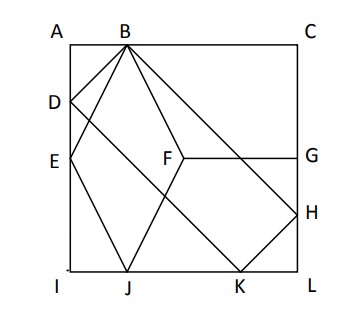
$1)$ Dans cette figure se cache…
a. … un rectangle. Quel est son nom ? …………….
b. … un losange. Quel est son nom ? …………….
c. … deux trapèzes. Quels sont leurs noms ? …………….
$2)$ Quelle est la nature…
a. … du quadrilatère $EGLI$ ? …………………………………………………..
b. … du quadrilatère $BDIC $? …………………………………………………..
c. … du quadrilatère $FGKJ$ ? …………………………………………………..
d. … du quadrilatère $CDJH$ ? …………………………………………………..
e. … du quadrilatère $BEJG$ ? …………………………………………………..
$1)$
a. $BHKD$.$
b. $EBFJ$
c. $BCGF$ et $FGLJ$
$2)$
a. C’est un rectangle.
b. C’est un trapèze.
c. C’est un trapèze.
d. C’est un quadrilatère quelconque.
e. C’est un quadrilatère quelconque / un cerf volant.
Exercice 9:
$1)$ Les deux quadrilatères ci-dessous sont-ils des rectangles ? Justifier la réponse.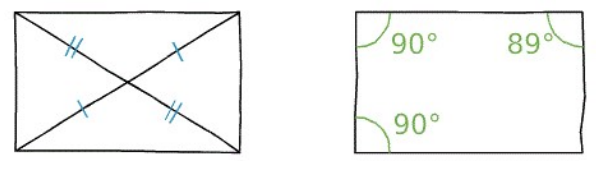
$2)$
$a)$ Montrer que le quadrilatère $RSTU$ est un parallélogramme.
$b)$ Peut-on être plus précis sur la nature du quadrilatère $RSTU$ ? Justifier la réponse.

$1)$
Figure 1 : Les diagonales du quadrilatère n’ont pas la même longueur donc ce n’est pas un rectangle.
Figure 2 : Les angles du quadrilatère n’ont pas la même mesure $( 90°)$ donc ce n’est pas un rectangle.
$2)$
$a)$ Les diagonales du quadrilatère $RSTU$ se coupent en leur milieu donc $RSTU$ est un parallélogramme.
$b)$ $RÛT = 90°$ Un parallélogramme qui a un angle droit est un rectangle.
Donc $RSTU$ est un rectangle.
Exercice 10:
Tracer les figures suivantes en respectant les mesures indiquées :
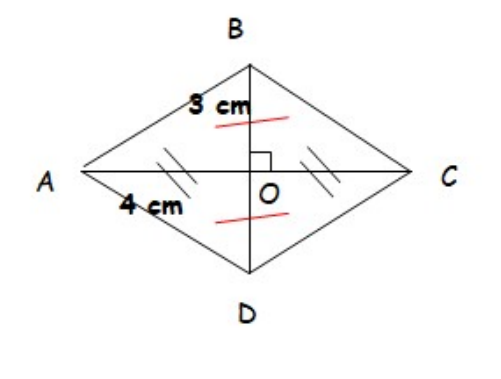
$1)$ Construire le losange $ABCD$ de centre $O$ tel que $OA = 4 cm$ et $OB = 3 cm$.
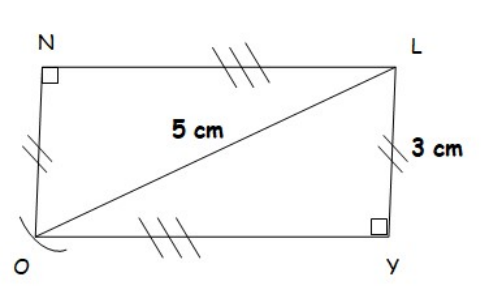
$2)$ Construire le rectangle $LYON$ tel que $LY = 3 cm, LO = 5 cm$.
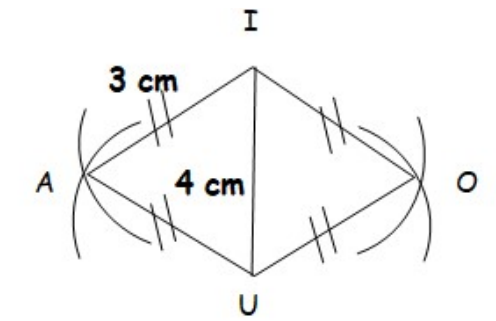
$3)$ Construire le losange $AIOU$ tel que $AI = 3 cm$ et $AO = 4 cm$.
$1)$
$2)$
$3)$
Exercice 11:
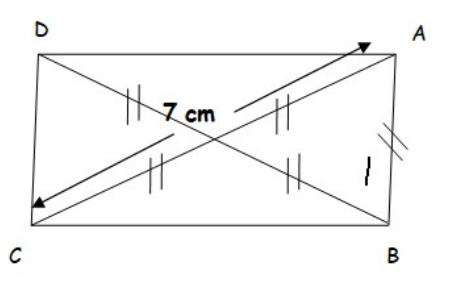
$1)$ Construire un rectangle $ABCD$ tel que $AC = 7 cm$.
$2)$ Construire un carré $EFGH$ tel que $FH = 4 cm$.
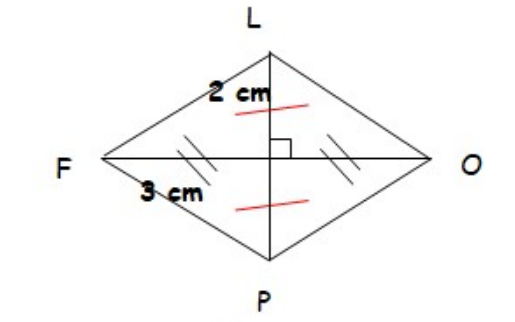
$3)$ Construire le losange $FLOP$ tel que $FO = 6 cm$ et $LP = 4 cm$.
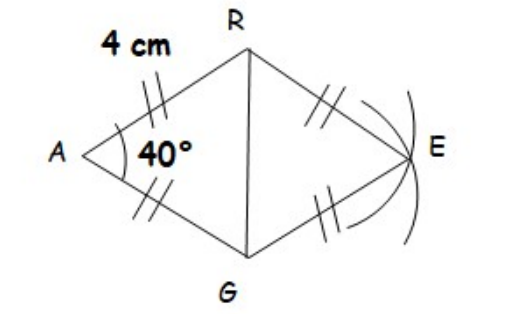
$4)$ Construire le losange $RAGE$ tel que $RA = 4 cm$ et$ RÂG = 40°$.
$1)$
$2)$

$3)$
$4)$
Exercice 12:
Pour chacune des figures suivantes, indiquer les numéros des propriétés qu’elle possède :
Parallélogramme : _________________
Rectangle : ______________________
Losange : _______________________
Carré : __________________________
$1)$ Les côtés opposés sont parallèles
$2)$ Les côtés opposés ont la même longueur
$3)$ Les angles opposés sont de même mesure
$4)$ Les quatre angles sont droits
$5)$ Les diagonales ont le même milieu
$6)$ Les diagonales ont la même longueur
$7)$ Les diagonales sont perpendiculaires*
$8)$ Les quatre côtés ont la même longueur
Pour chacune des figures suivantes, indiquer les numéros des propriétés qu’elle possède :
Parallélogramme : $1) 2) 3) 5)$
Rectangle : $1) 2) 3) 4) 5) 6)$
Losange : $1) 2) 3) 5) 7) 8)$
Carré : $1) 2) 3) 4) 5) 6) 7) 8)$
Exercice 13:
$AB=BR ; EB=BC$ ; les angles $ADC, DCB$ et $BAD$ sont droits.
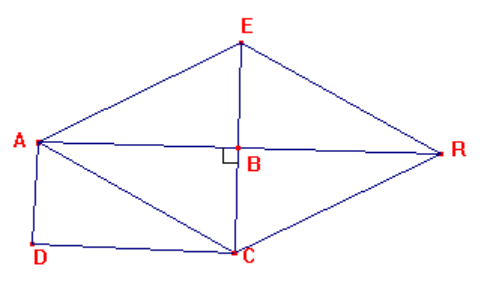
$1)$ Quelle est la nature du quadrilatère $ABCD$ ?
$2)$ Que peux tu dire des droites $(AR)$ et $(EC)$ ?
$3)$ Que représentent $[AR]$ et $[EC]$ pour le quadrilatère $AERC$ ?
$4)$ Donne la nature du quadrilatère $AERC$.
$1)$ Le quadrilatère $ABCD$ a $4$ angles droits donc c’est un rectangle.
$2)$ Les droites $(AR)$ et $(EC)$ sont perpendiculaires (voir figure).
$3)$ $[AR]$ et $[EC]$ sont les diagonales du quadrilatère $AERC$.
$4)$ $AERC$ est un quadrilatère dont les diagonales sont perpendiculaires et se coupent en leur milieu.
Conclusion :
$AERC$ est losange. La figure est facultative, cependant elle permet de résoudre rapidement l’exercice.
Exercice 14:
$1)$ Trace un rectangle $ABCD$ dont les diagonales se coupent en $E$. Puis le parallélogramme $AEBF$. $(EF)$ et $(AB)$ se coupent en $I$.
Trace le parallélogramme $EIBJ$.
$2)$ Quelle est la nature de $AEBF$ ? Justifie ta réponse.
$3)$ Que peux-tu dire des deux droites $(EF)$ et $(AB)$ ? Justifie ta réponse.
$4)$ Quelle est la nature de $EIBJ$ ? Justifie ta réponse.
$1)$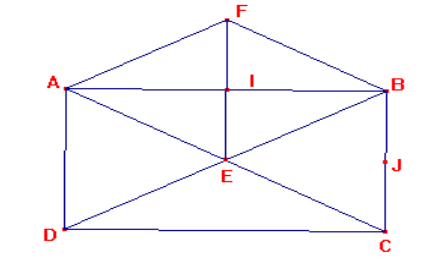
$2)$ Le quadrilatère $AEBF$ est un losange car C’est un parallélogramme qui a deux côtés consécutifs $[AE]$ et $[EB]$ de même longueur.
$3)$ les droites $(EF)$ et $(AB)$ sont perpendiculaires car elles sont les diagonales du losange $AEBF$.
$4)$ $IBJE$ est un rectangle. $(EI) //(BJ)$, $(IB)//(EJ)$ et l’angle $IBJ$ est un angle droit donc c’est un parallélogramme qui a un angle droit.
Parallélogramme et quadrilatères particuliers