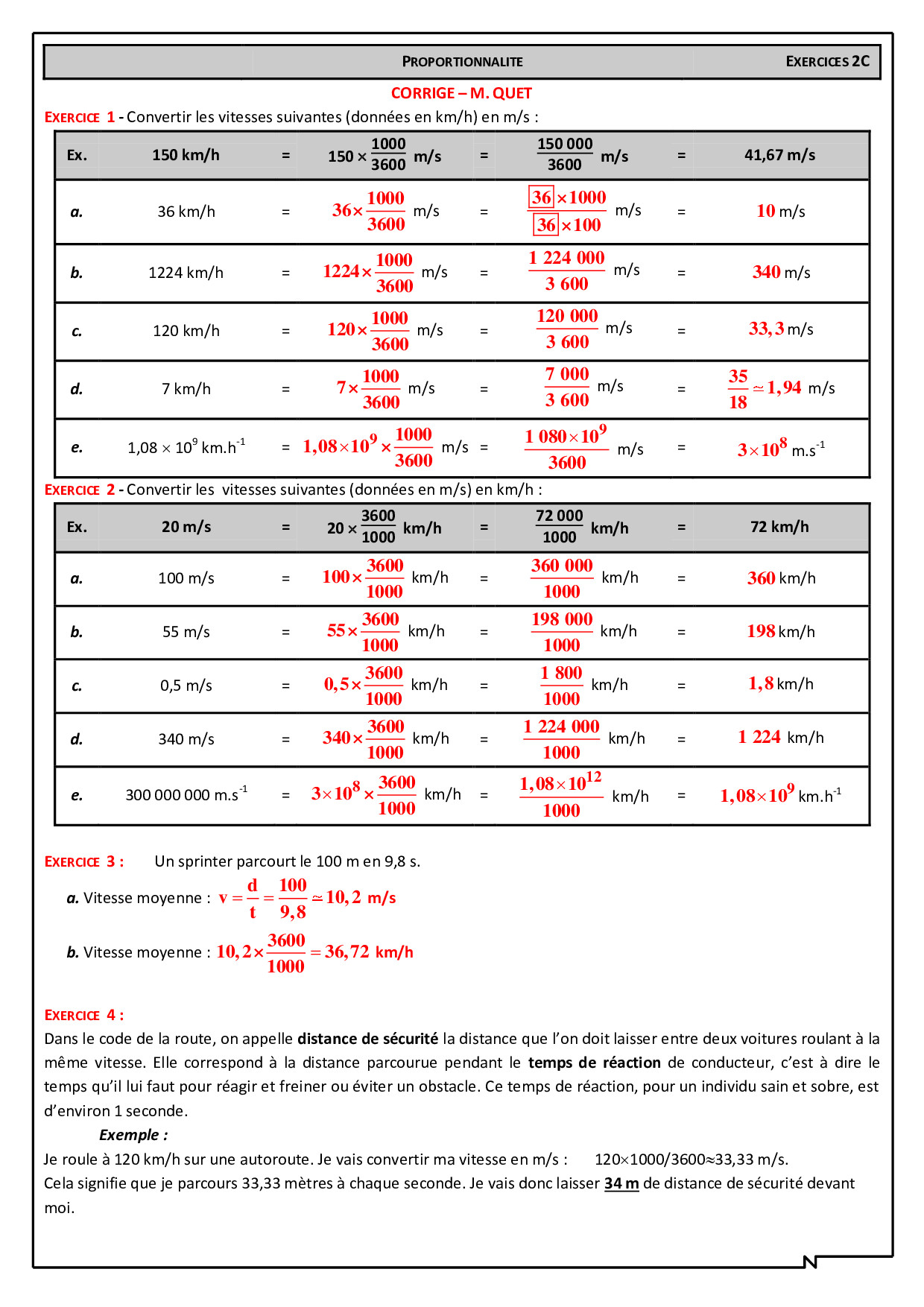
Cours
Exercices corrigés
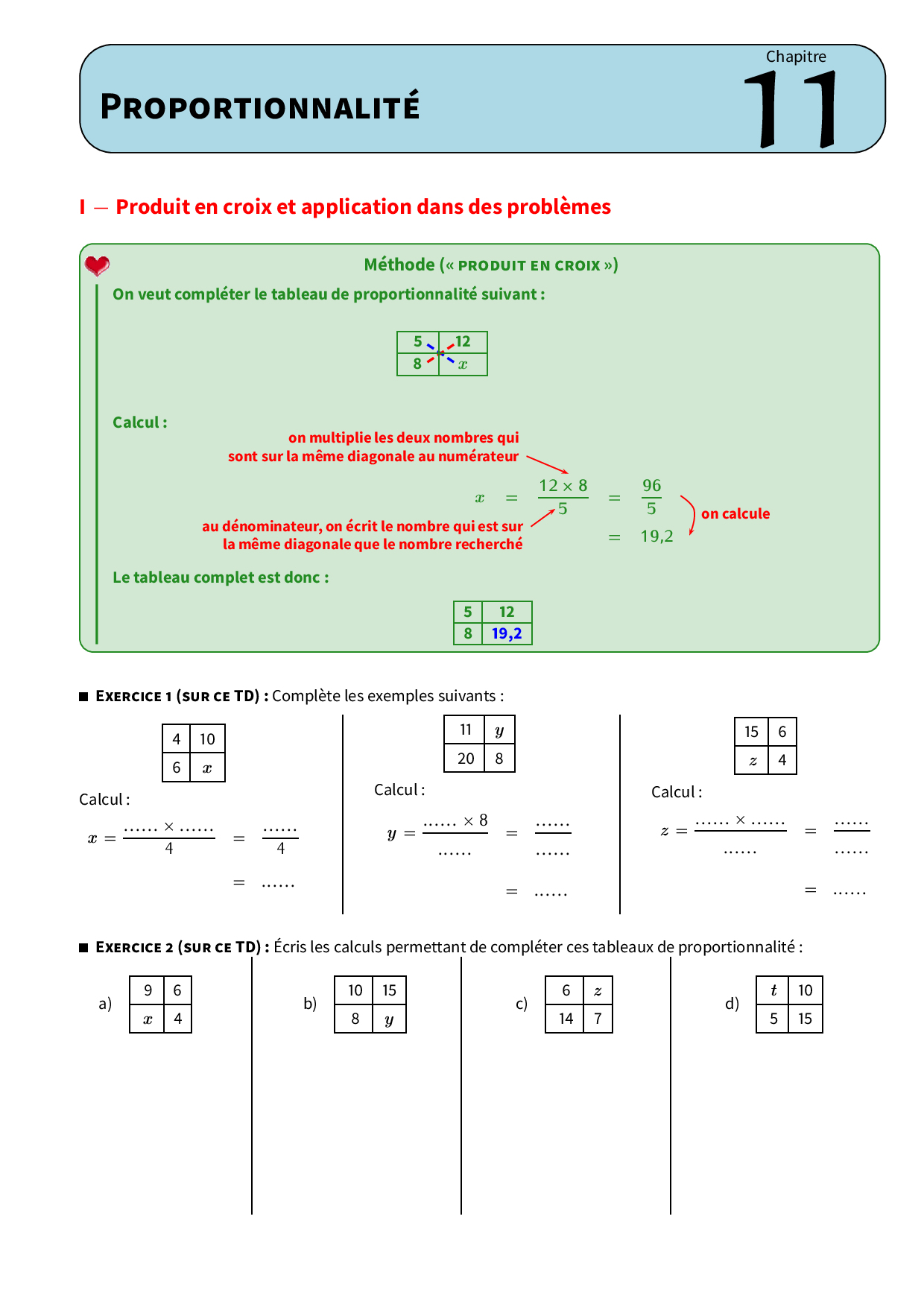
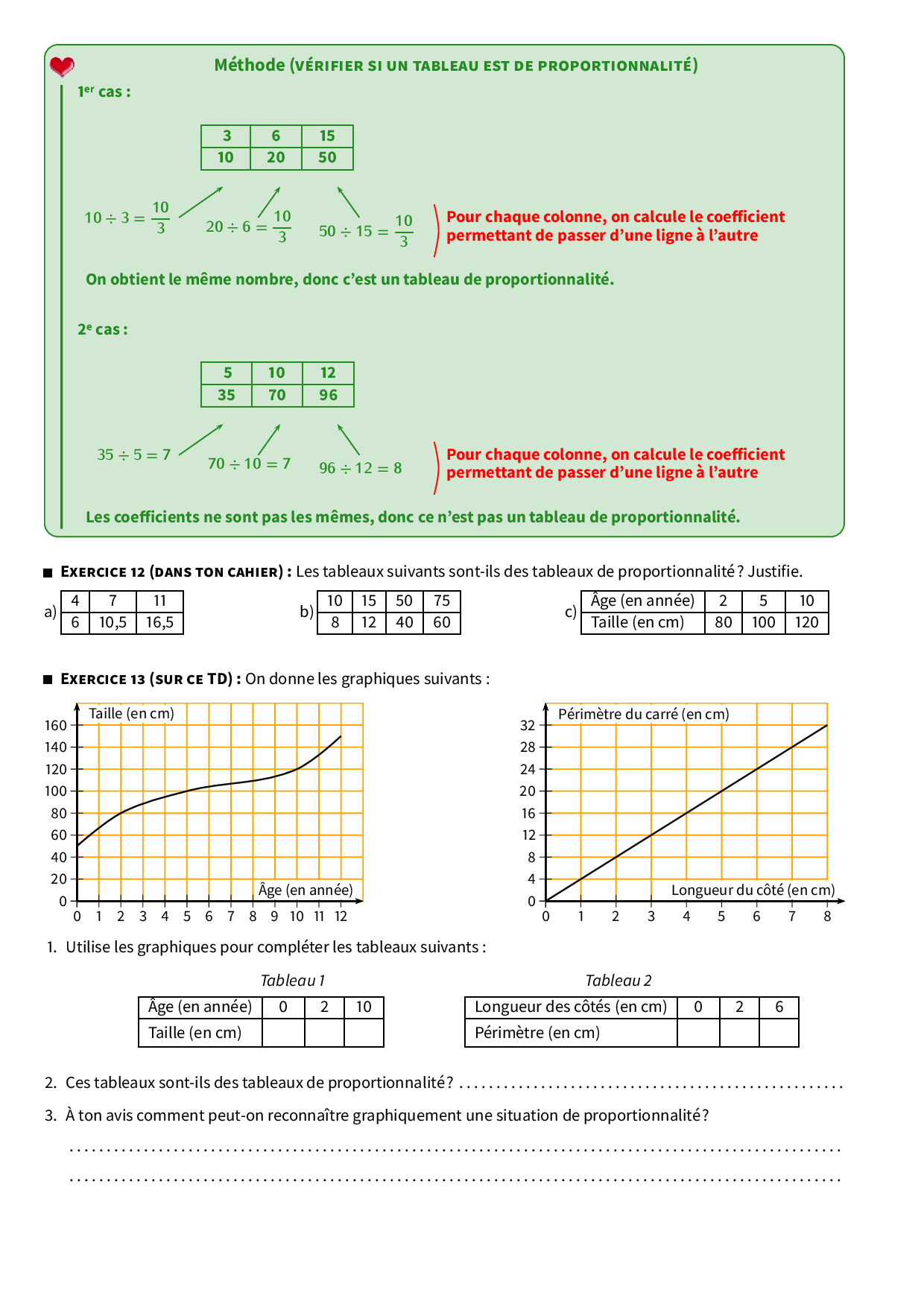
Tableaux de proportionnalité
Calculs de pourcentages
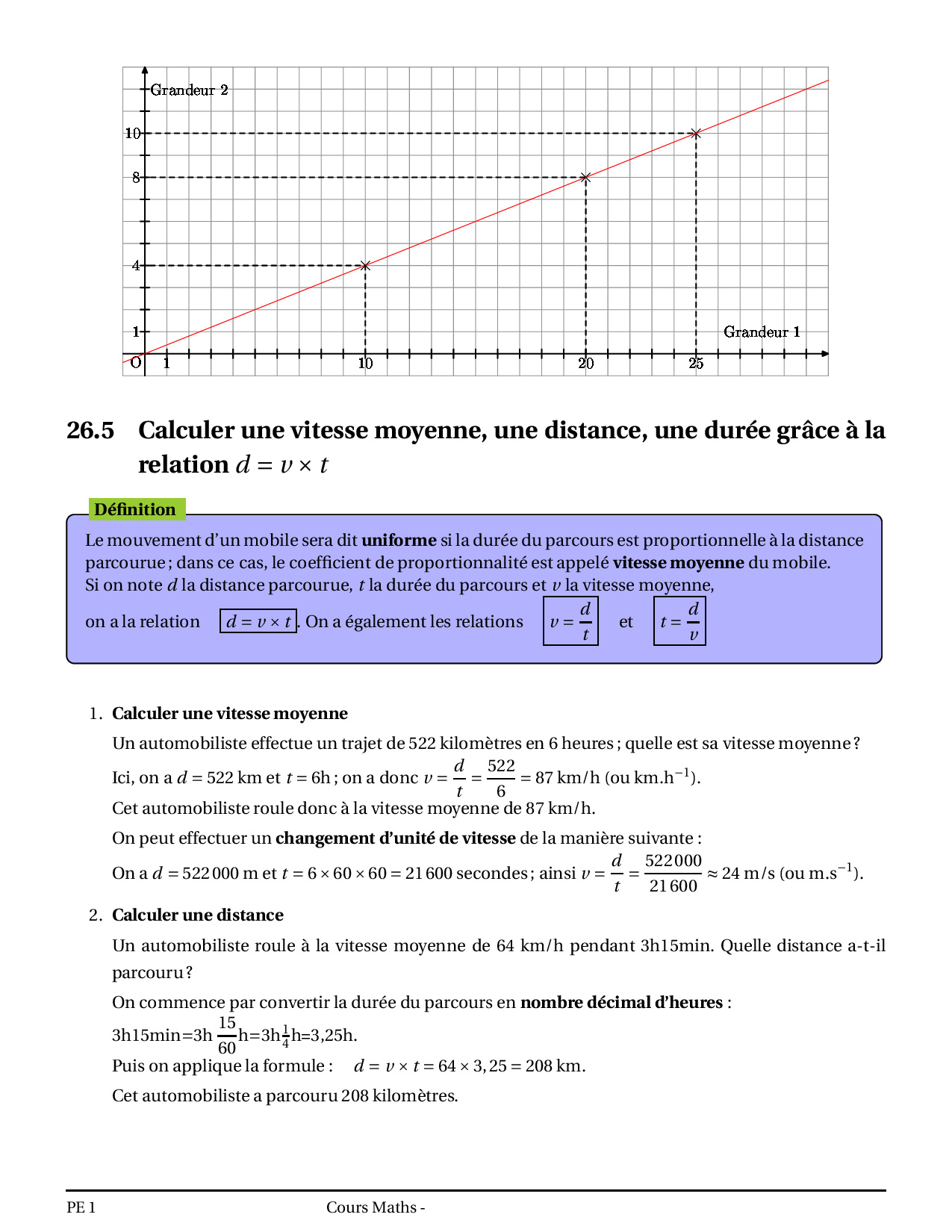
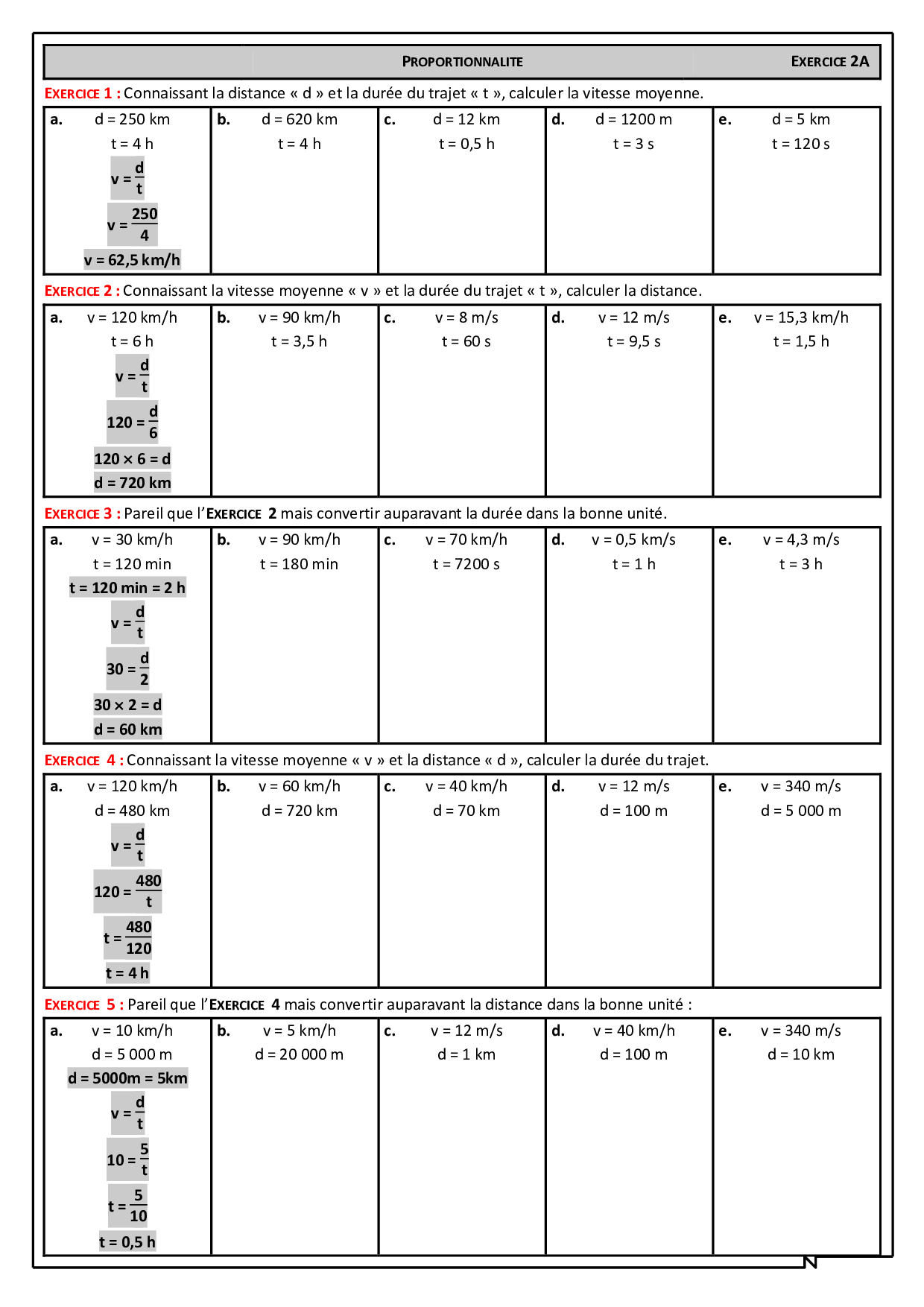
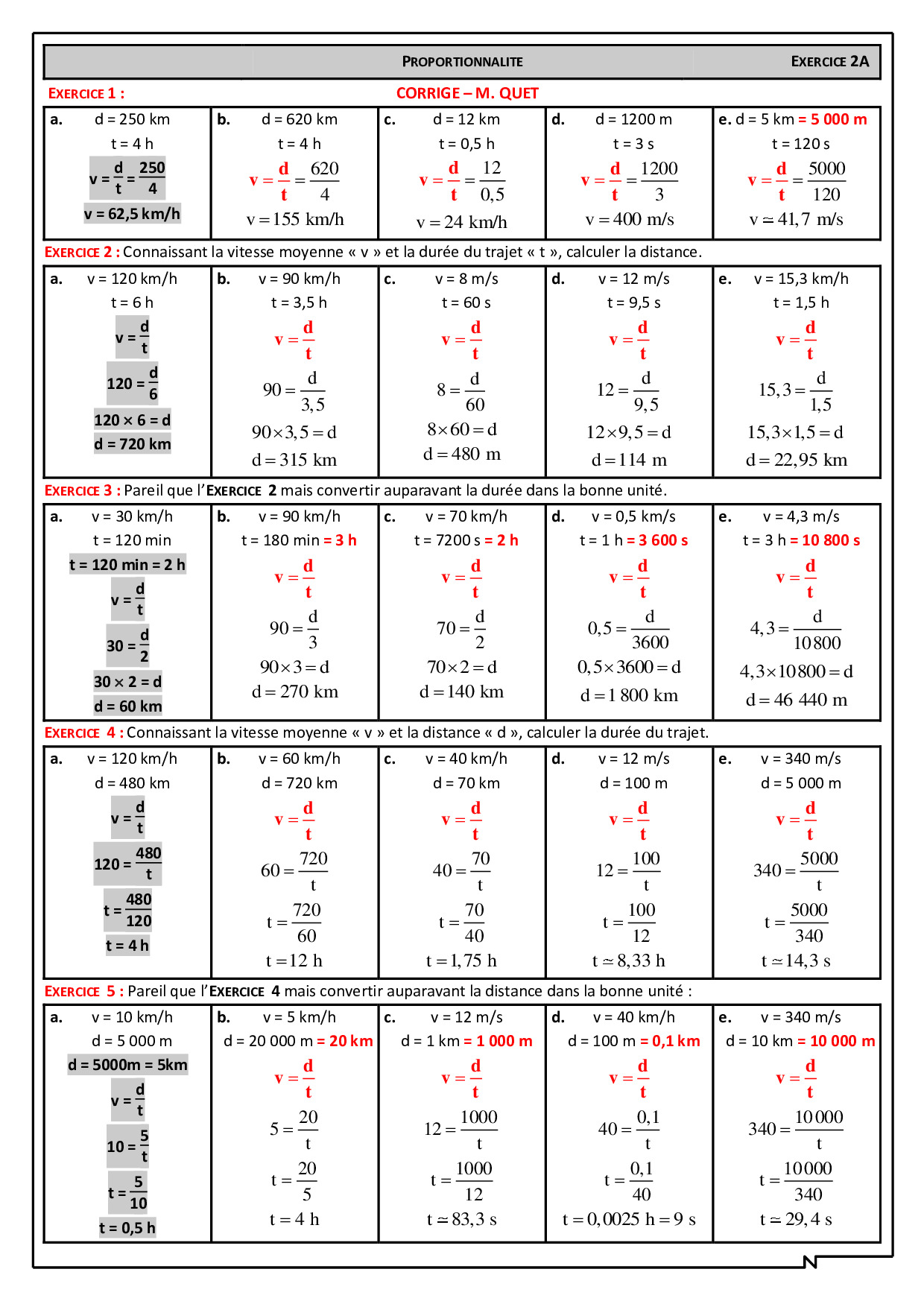
Vitesse moyenne
Vitesse moyenne -Problemes
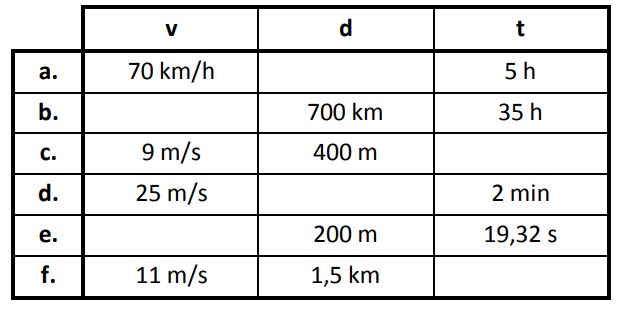
EXERCICES 1: Compléter les cases vides du tableau :
EXERCICE 2 : « MARIE-JO »
Marie-Jo parcourt le 400 m en 50 secondes.
a. Quelle est sa vitesse moyenne (en m.s-1) sur cette distance ?
b. On s’est rendu compte que la vitesse moyenne sur les 200 derniers mètres était de 9 m.s-1
. Quel temps lui faut-il pour parcourir ces 200 mètres ?
c. A quelle vitesse moyenne l’athlète parcourt-elle les
200 premiers mètres ?
EXERCICE 3 : « 24 H DU MANS »
a. La BMW V12 LMR a gagné en 1999 en parcourant 4967,991 km.
Quelle a été sa vitesse moyenne ?
b. En 1978, le Renault-Alpine A 442B l’a emporté à une vitesse moyenne de 210,188 km/h.
Quelle distance a-t-elle parcouru ?
c. En 1978, le circuit mesurait 13,634 km, alors qu’en 1999, il mesurait 13,611 km.
Combien de tours de circuits ont été nécessaires aux deux voitures pour l’emporter ?
EXERCICE 4 : « ALLER-RETOUR »
Un automobiliste effectue un aller-retour entre son travail et son domicile, séparés de 60 km. A l’aller, il roule à 100 km/h ; au retour, il roule à 40 km/h.
a. Quel temps a-t-il mis à l’aller ?
b. Quel temps a-t-il mis au retour ?
c. Quelle a été sa vitesse moyenne sur l’ensemble du trajet aller-retour ?
EXERCICE 5 : TRANSATLANTIQUE
Un avion décolle de Paris et arrive à Chicago 7h plus tard. Au retour, il mettra 1h de plus.
Sachant qu’entre les deux villes l’avion parcourt 6 900 km,
quelle est sa vitesse moyenne sur l’aller-retour ?
EXERCICE 6 :On peut partager les coureurs cyclistes en 3 catégories : Les « grimpeurs », les « rouleurs » et les « sprinteurs ». On a récapitulé leurs vitesses moyennes en fonction du type de terrain dans ce tableau :
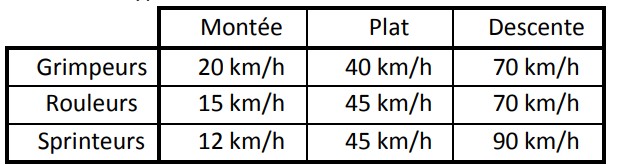
Calculer le temps que réalisera chaque type de coureur sur cette étape :