Proportionnalité et fonctions linéaires

1)  Situation de proportionnalité

a) Suites proportionnelles :

Deux suites de nombres x et y sont proportionnelles, si on obtient tous les nombres de la suite y en multipliant tous les nombres de la suite x par un même nombre k.

b) Tableau de proportionnalité :

On a donc : y = k * x.
-Le nombre k s’appelle le coefficient de proportionnalité de la suite x vers la suite y.
– On a aussi : x = a/100 et k = y/ x .

c) Graphique :

Propriété1 : Le graphique d’une situation de proportionnalité, (ou représentant un tableau de proportionnalité), est constitué de points alignés avec l’origine.
Propriété2 : Si les points d’une représentation graphique sont alignés avec l’origine, le graphique représente une situation de proportionnalité.

d) Exemples :

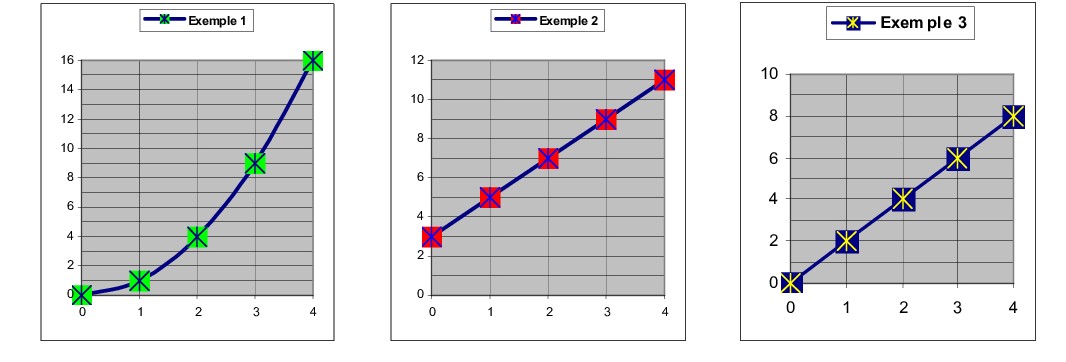
Les points de ce graphique                                                    Les points de ce graphique                                                        Les points de ce graphique
ne sont pas alignés.                                                                 sont alignés mais pas avec                                                        sont alignés, avec l’origine.
Ce n’est pas une situation                                                         l’origine. Ce n’est pas une situation                                      C’est une situation de
de proportionnalité.                                                                  de proportionnalité.                                                                proportionnalité.

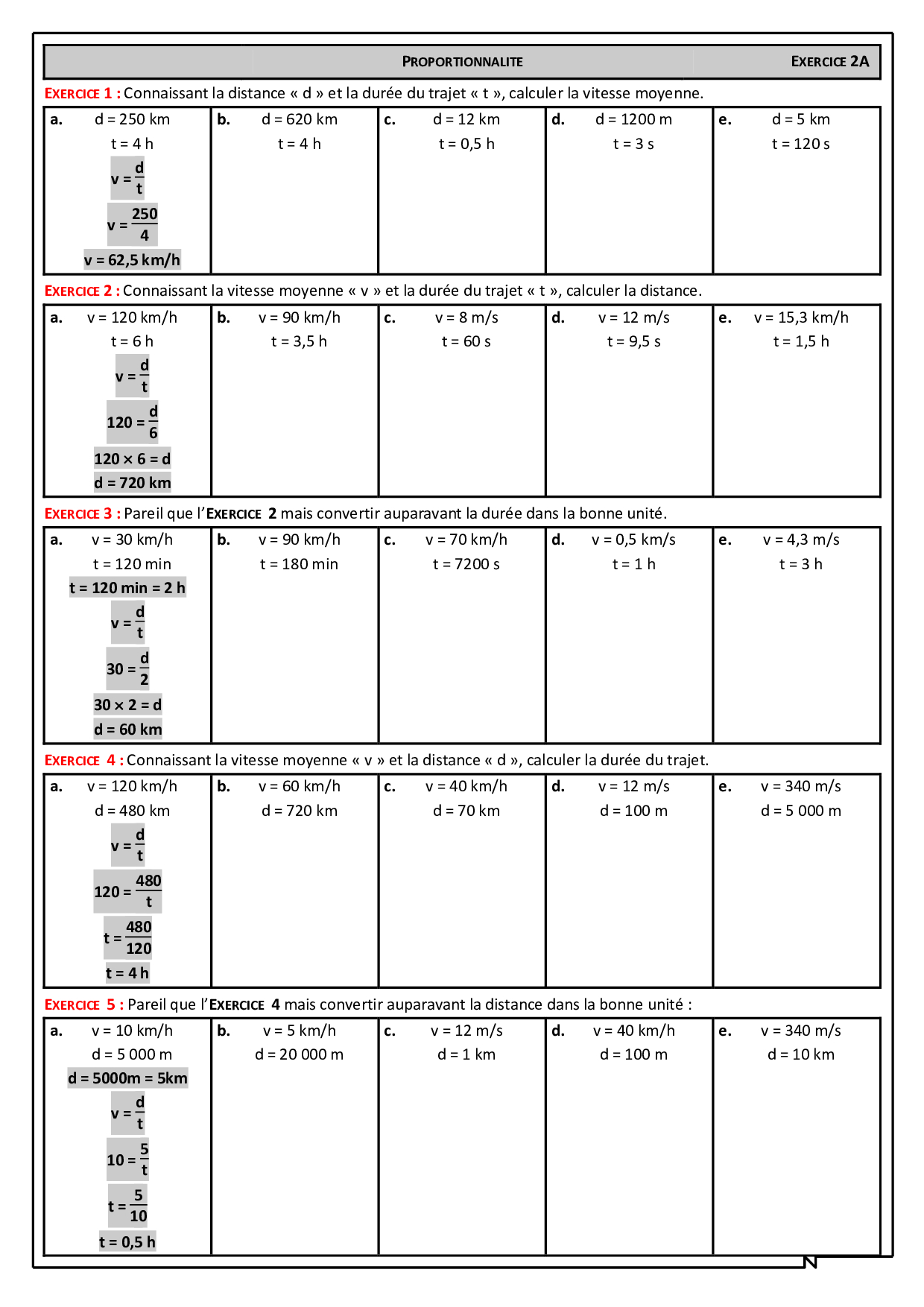
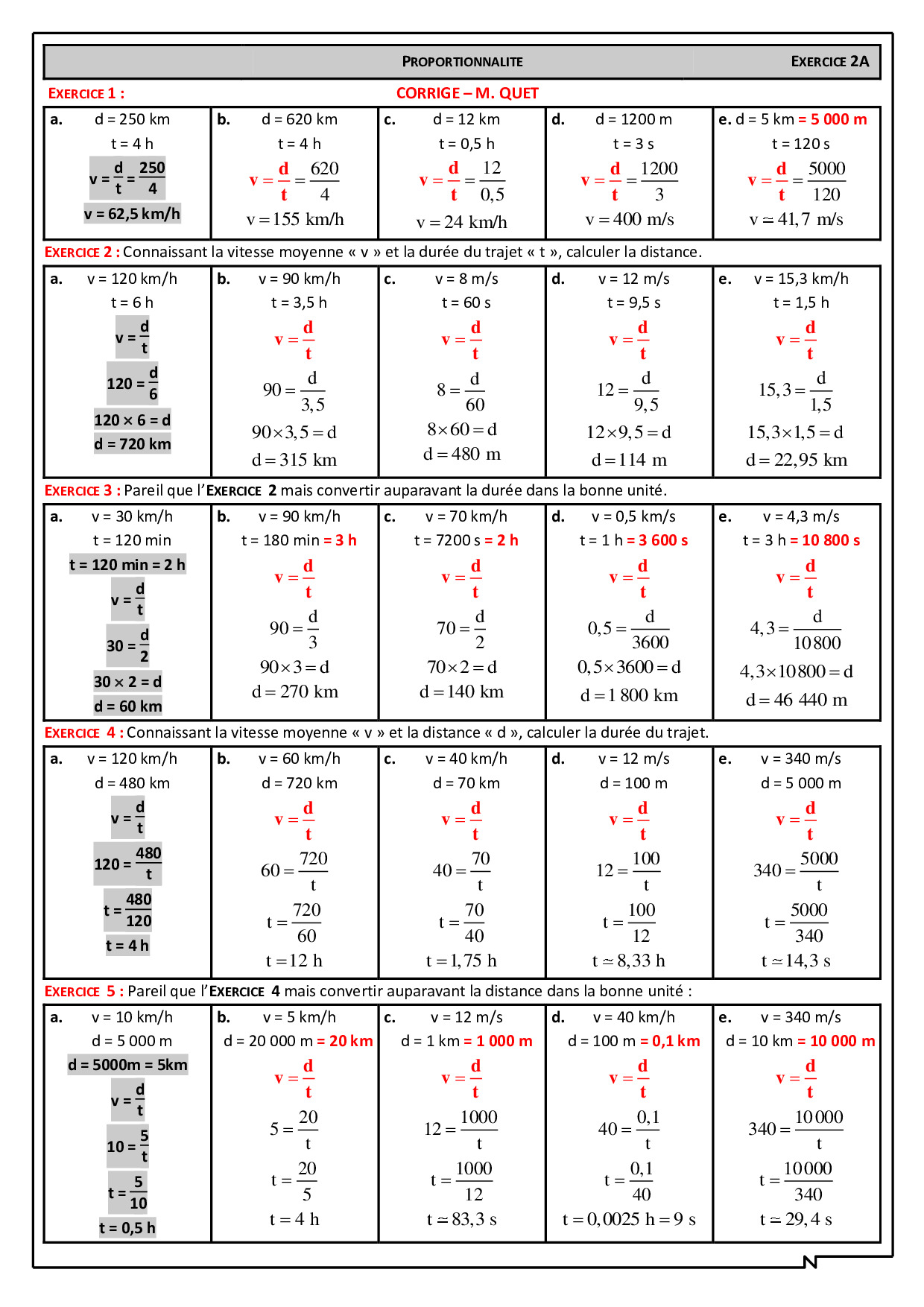
2) Vitesse moyenne

a) Formule :

D: est la distance parcourue
T: est la durée ou le temps de parcours
V: est la vitesse
Alors, à vitesse constante, les distances sont proportionnelles aux durées, et le coefficient de proportionnalité entre les temps et distances est la vitesse.

V =D/T       ; D=V*T                 et  T=D/V

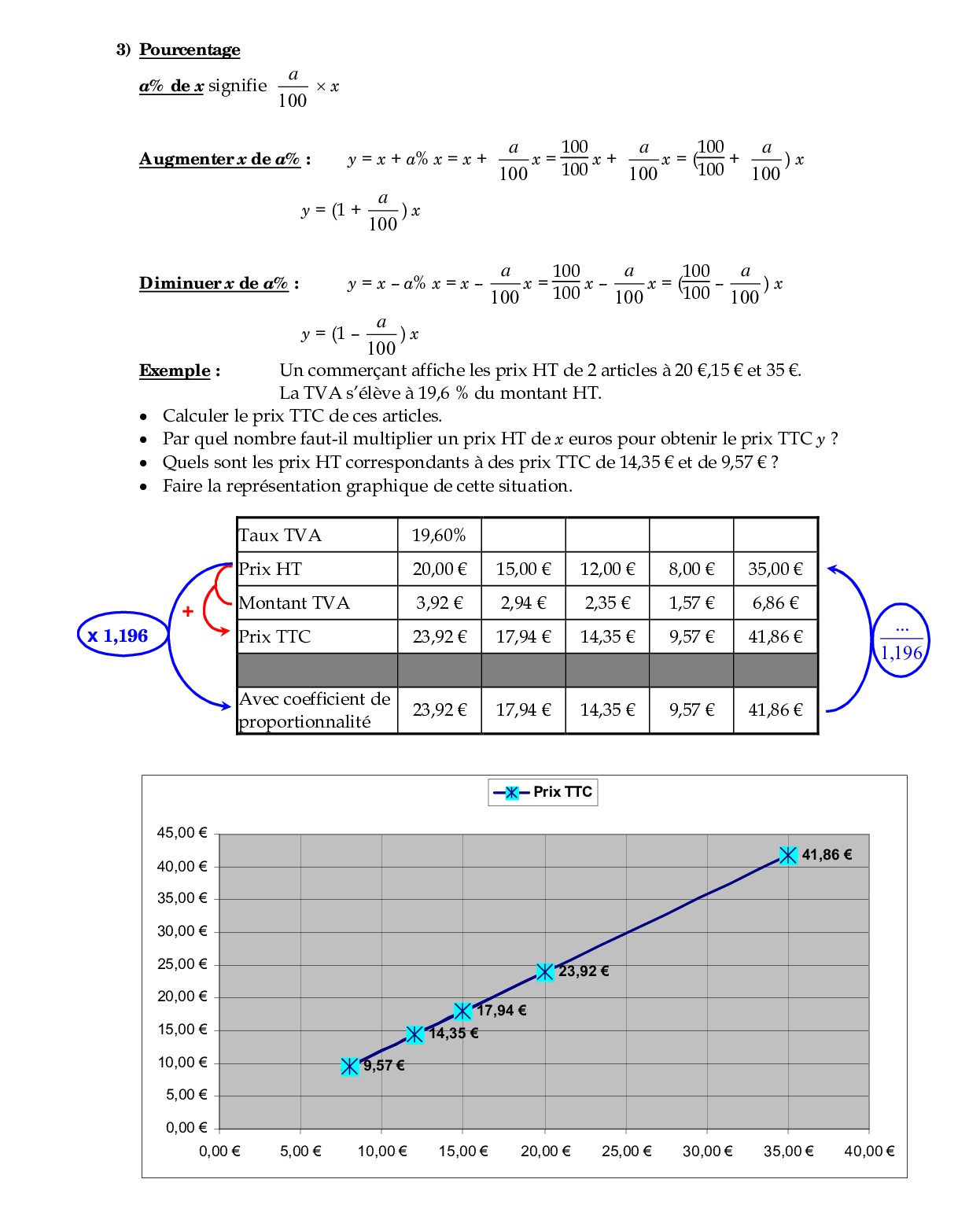
b) Exemple :

Un automobiliste parcourt 120 km en 1h30, en roulant É vitesse constante.
-Calculer sa vitesse.
-Quelle distance parcourt il en 36 min ? en 2h06 ?
– Quel temps met-il pour parcourir 16 km ? 64 km ?
– Tracer le graphique représentant toutes les valeurs de cette situation.
– Que constatez vous ?

Solution :
1h30 =3/2 h =1.5h . Donc V=120/1.5 =80km/h
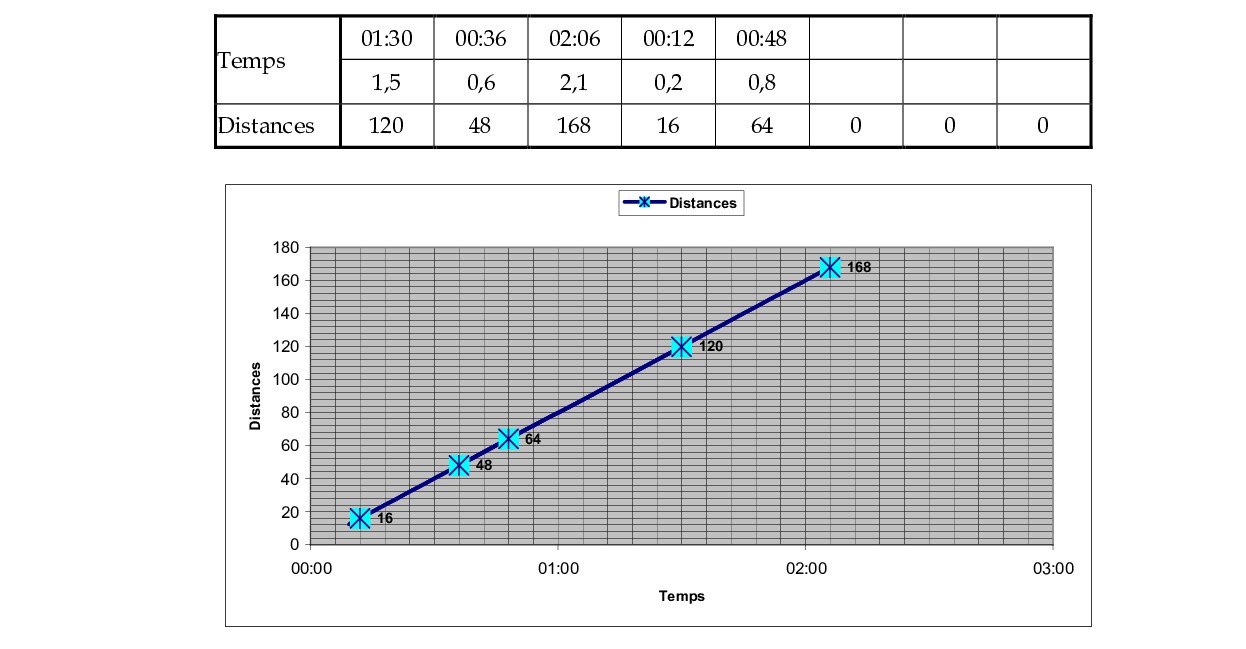
– Pour les 2ème et 3ème questions, on peut répondre sur un tableau de proportionnalité.
 -On trace alors le graphique, avec en abscisses les temps (6 cm pour 1 h), et en ordonnées les distances (1 cm pour 20 km)
– On constate que les points sont alignés avec l’origine.