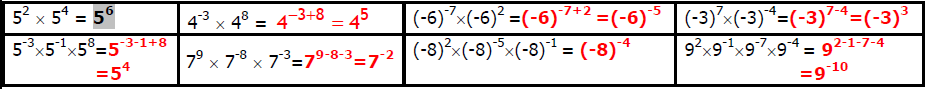Puissances exercices corrigés 1AC
Puissances exercices corrigés 2AC
Exercice 1:
Calculer :
$(-4)^{3}=$
$5^{4}=$
$(-6)^{3}=$
$2^{6}=$
$(-10)^{3}=$
$2^{8}=$
$(-3)^{4}=$
$(0,1)^{3}=$
$(-5)^{5}=$
$(-100)^{5}=$
$(-4)^{3}=(-4) \times(-4) \times(-4)=-64$
$5^{4}=5 \times 5 \times 5 \times 5=625$
$(-6)^{3}=(-6) \times(-6) \times(-6)=-216$
$2^{6}=2 \times 2 \times 2 \times 2 \times 2 \times 2=64$
$(-10)^{3}=(-10) \times(-10) \times(-10)=-1000$
$2^{8}=2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2=256$
$(-3)^{4}=(-3) \times(-3) \times(-3) \times(-3)=81$
$(0,1)^{3}=0,1 \times 0,1 \times 0,1=0,001$
$(-5)^{5}=(-5) \times(-5) \times(-5) \times(-5) \times(-5)=-3125$
$(-100)^{5}=(-100) \times(-100) \times(-100) \times(-100) \times(-100)=-10000000000$
Exercice 2:
Dans les exemples suivants, déterminer ce qui doit être répété lorsqu’on développe la puissance.
• (-2)3 = ? Est-ce que 2 est répété 3 fois ?
Est-ce que le signe – est répété 3 fois ?
Quelle est la base ?
• -35 = ? Est-ce que 3 est répété 5 fois ?
Est-ce que le signe – est répété 5 fois ?
Quelle est la base ?
• -(5)4 = ? Est-ce que 5 est répété 4 fois ?
Est-ce que le signe – est répété 4 fois ?
Quelle est la base ?
• (-73) = ? Est-ce que 7 est répété 3 fois ?
Est-ce que le signe – est répété 3 fois ?
Quelle est la base ?
• ((-3)2) = ? Est-ce que 3 est répété 2 fois ?
Est-ce que le signe – est répété 2 fois ?
Quelle est la base ?
• -(43) = ? Est-ce que 4 est répété 3 fois ?
Est-ce que le signe – est répété 3 fois ?
Quelle est la base ?
• (-(6)3) = ? Est-ce que 6 est répété 3 fois ?
Est-ce que le signe – est répété 3 fois ?
Quelle est la base ?
• -24 = ? Est-ce que 2 est répété 4 fois ?
Est-ce que le signe – est répété 4 fois ?
Quelle est la base ?
• (-2)3 = ? Est-ce que 2 est répété 3 fois ? OUI
Est-ce que le signe – est répété 3 fois ? OUI
Quelle est la base ? -2
• -35 = ? Est-ce que 3 est répété 5 fois ? OUI
Est-ce que le signe – est répété 5 fois ? NON
Quelle est la base ? 3
• -(5)4 = ? Est-ce que 5 est répété 4 fois ? OUI
Est-ce que le signe – est répété 4 fois ? NON
Quelle est la base ? 5
• (-73) = ? Est-ce que 7 est répété 3 fois ? OUI
Est-ce que le signe – est répété 3 fois ? NON
Quelle est la base ? 7
• ((-3)2) = ? Est-ce que 3 est répété 2 fois ? OUI
Est-ce que le signe – est répété 2 fois ? OUI
Quelle est la base ?-3
• -(43) = ? Est-ce que 4 est répété 3 fois ? OUI
Est-ce que le signe – est répété 3 fois ? NON
Quelle est la base ? 4
• (-(6)3) = ? Est-ce que 6 est répété 3 fois ? OUI
Est-ce que le signe – est répété 3 fois ? NON
Quelle est la base ? 6
• -24 = ? Est-ce que 2 est répété 4 fois ? OUI
Est-ce que le signe – est répété 4 fois ? NON
Quelle est la base ? 2
Exercice 3:
$1)$ Compléter le tableau suivant :
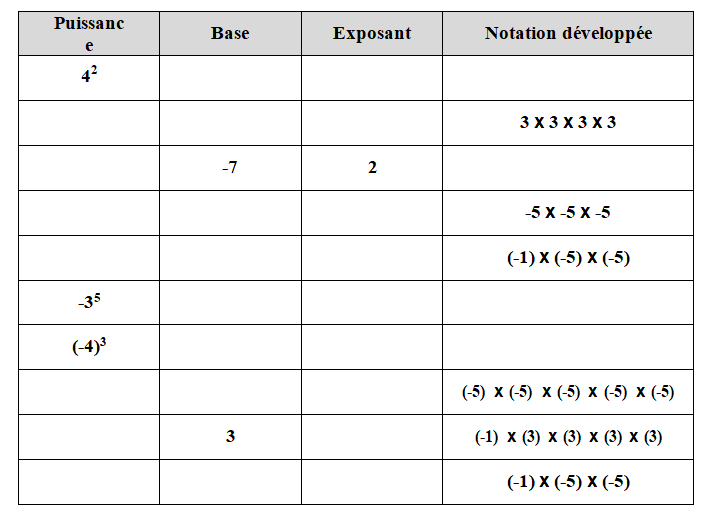
$2)$ Déterminer le signe de :
$a. $23^{42}$
b. $(-15)^{20}$
c. $(-35)^{17}$
d. $(19)^{32}$
e. $(-51)^{13}$
f. $(-27)^{20}$
g. $-(18)^{12}$
h. $-19^{32}$
$1)$
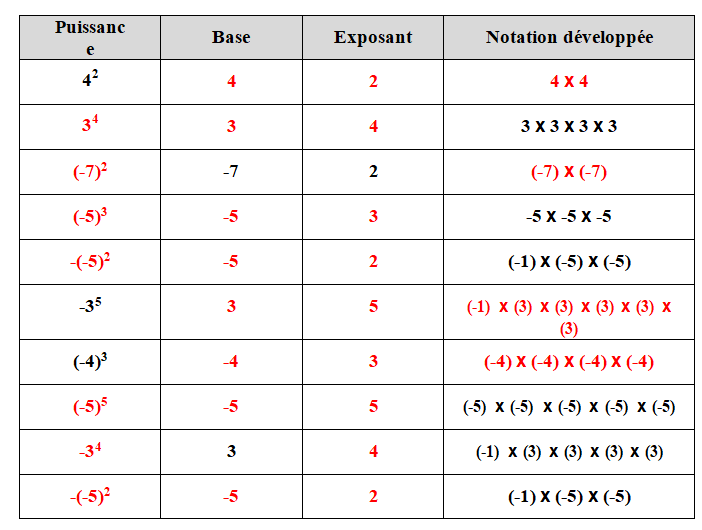
$2)$ Déterminer le signe de :
$a. $23^{42}$ Positif
b. $(-15)^{20}$ Positif
c. $(-35)^{17}$ Négatif
d. $(19)^{32}$ Positif
e. $(-51)^{13}$ Négatif
f. $(-27)^{20}$ Positif
g. $-(18)^{12}$ Négatif
h. $-19^{32}$ Négatif
Exercice 4:
Compléter par un nombre de la forme $a^{n}$ avec $a$ et $n$ entiers :
1. $\left(10^{4}\right)^{9}=$
2. $\frac{2^{10}}{2^{7}}=$
3. $\left(9^{10}\right)^{9}=$
4. $\frac{6^{11}}{6^{3}}=$
5. $7^{10} \times 7^{11}=$
6. $5^{6} \times 4^{6}=$
7. $11^{3} \times 2^{3}=$
8. $10^{2} \times 10^{9}=$
1. $\left(10^{4}\right)^{9}=10^{36}$
2. $\frac{2^{10}}{2^{7}}=2^{3}$
3. $\left(9^{10}\right)^{9}=9^{90}$
4. $\frac{6^{11}}{6^{3}}=6^{8}$
5. $7^{10} \times 7^{11}=7^{21}$
6. $5^{6} \times 4^{6}=20^{6}$
7. $11^{3} \times 2^{3}=22^{3}$
8. $10^{2} \times 10^{9}=10^{11}$
Exercice 5:
Compléter par un nombre de la forme $a^{n}$ avec $a$ et $n$ entiers :
1. $3^{5} \times 7^{5}=$
2. $\left(9^{8}\right)^{11}=$
3. $\frac{10^{11}}{10^{4}}=$
4. $\left(11^{3}\right)^{6}=$
5. $10^{9} \times 10^{2}=$
6. $3^{5} \times 2^{5}=$
7. $\frac{9^{8}}{9^{2}}=$
8. $2^{7} \times 2^{10}=$
1. $3^{5} \times 7^{5}=21^{5}$
2. $\left(9^{8}\right)^{11}=9^{88}$
3. $\frac{10^{11}}{10^{4}}=10^{7}$
4. $\left(11^{3}\right)^{6}=11^{18}$
5. $10^{9} \times 10^{2}=10^{11}$
6. $3^{5} \times 2^{5}=6^{5}$
7. $\frac{9^{8}}{9^{2}}=9^{6}$
8. $2^{7} \times 2^{10}=2^{17}$
Exercice 6:
Donner le résultat des calculs suivants sous la forme « $a^{n}$ » :
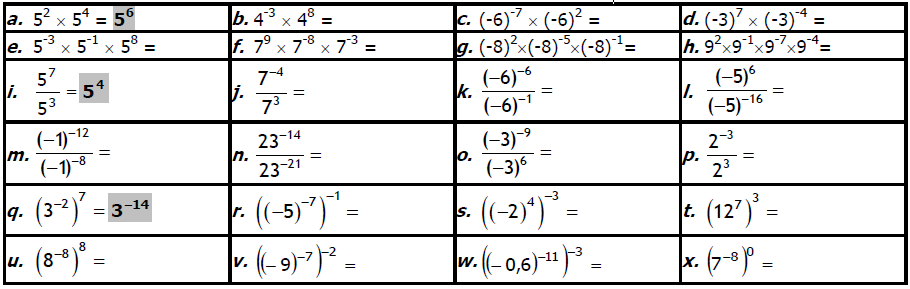
Exercice 7:
$1)$ Calculer mentalement :
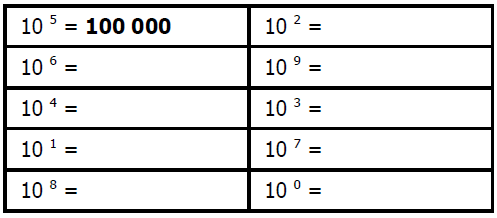
$2)$ Compléter les pointillés :

$1)$ Calculer mentalement :
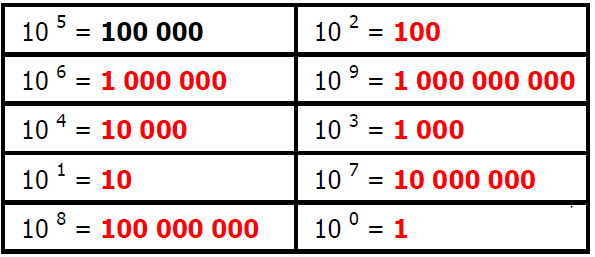
$1)$ Compléter les pointillés :
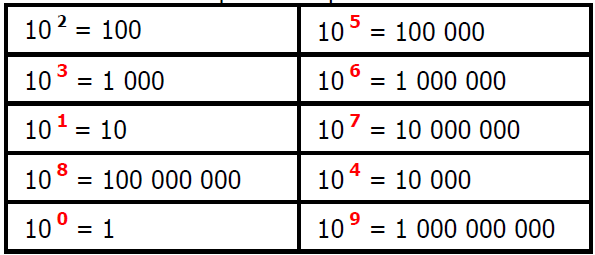
Exercice 8:
$1)$ Calculer mentalement :
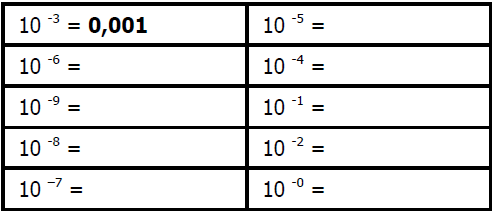
$2)$ Compléter les pointillés :

$1)$ Calculer mentalement :
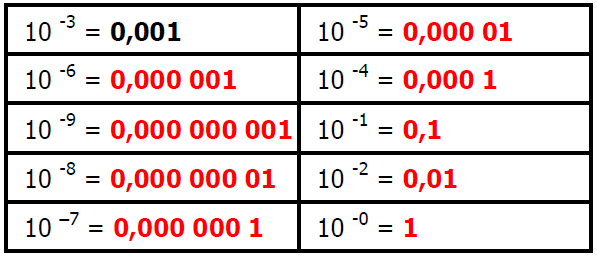
$2)$ Compléter les pointillés :
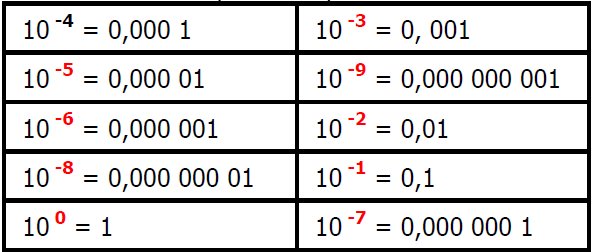
Exercice 9:
$1)$ Calculer mentalement :
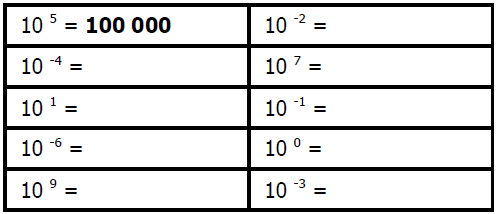
$2)$ Compléter les pointillés :
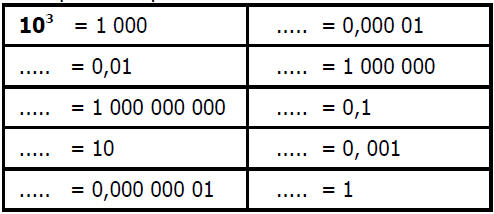
$1)$ Calculer mentalement :
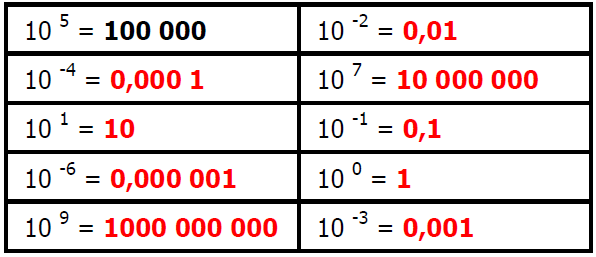
$2)$ Compléter les pointillés :

Exercice 10:
Donner le résultat des calculs suivants sous la forme « 10ª » :
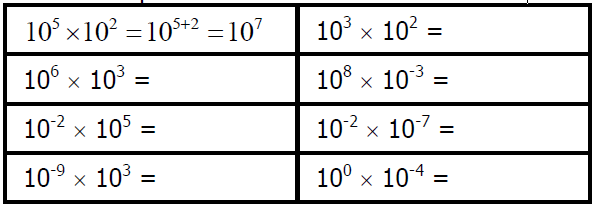

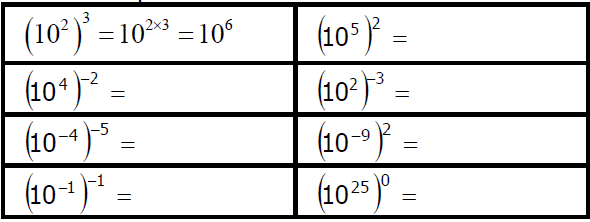
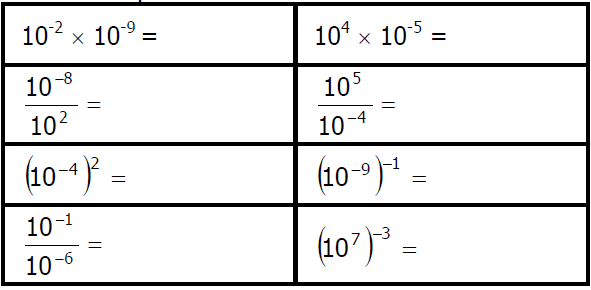
Donner le résultat des calculs suivants sous la forme « 10ª » :


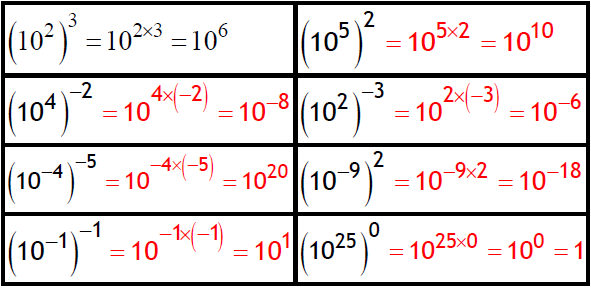
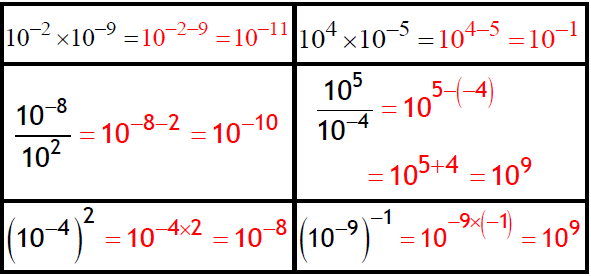
Exercice 11:
Parmi les nombres suivants, entourer ceux qui sont en écriture scientifique :
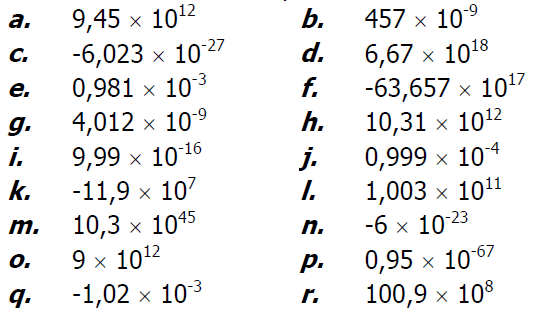
Exercice 12:
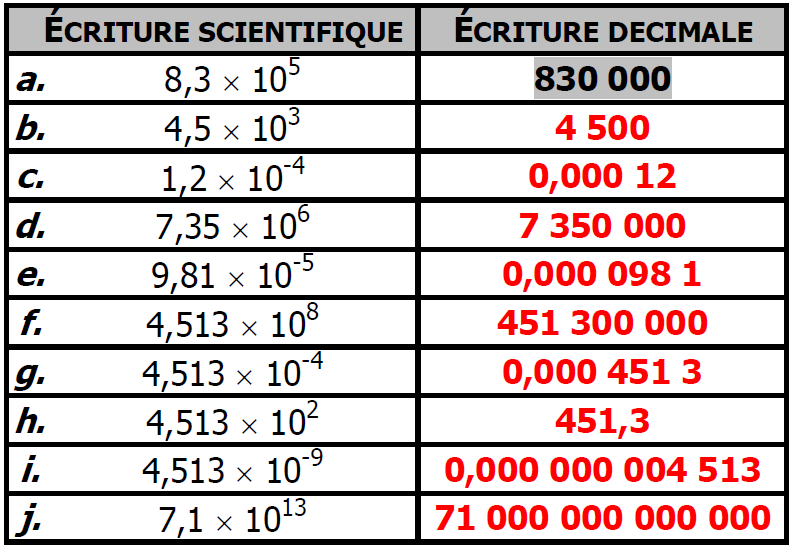
Compléter le tableau :
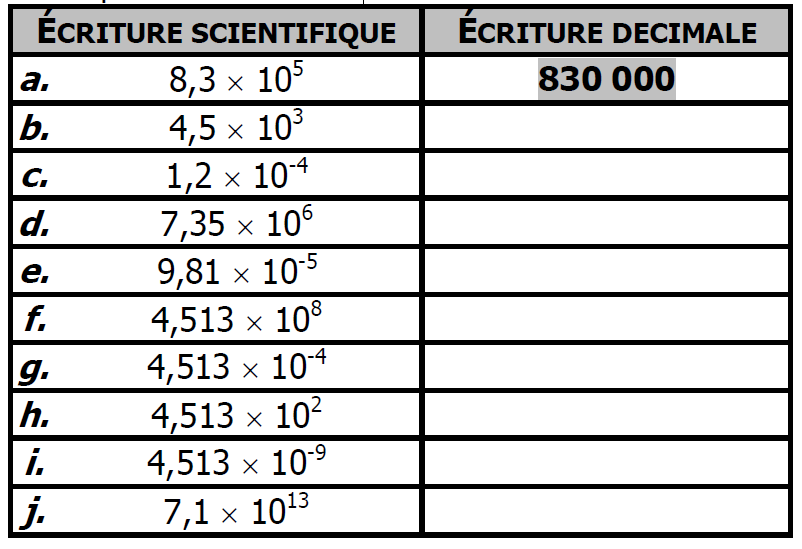
Exercice 13:
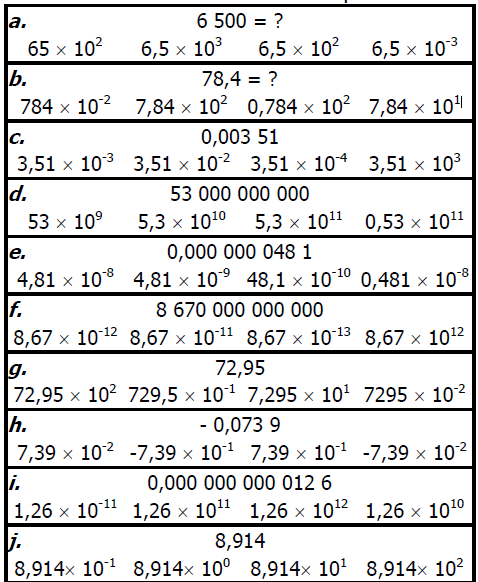
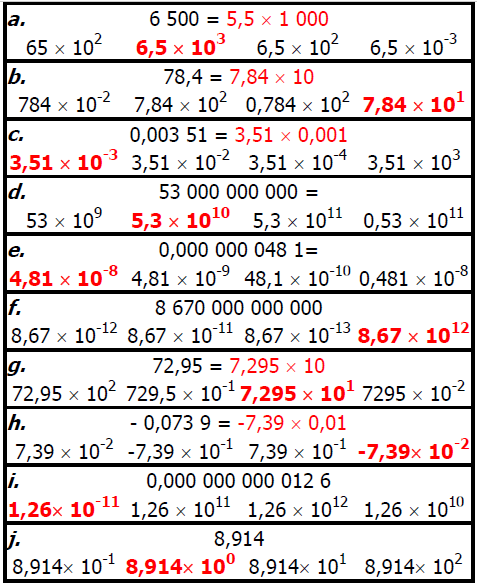
Retrouver la bonne écriture scientifique :
Exercice 14:
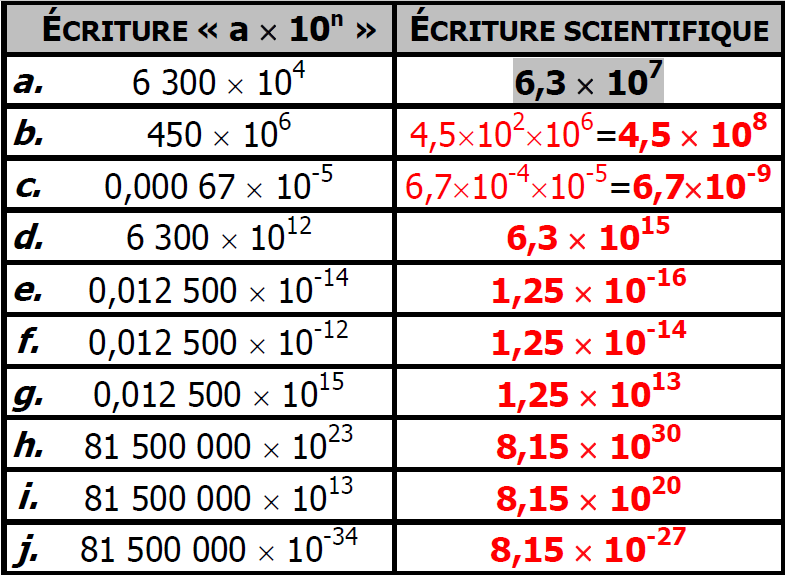
$1)$ Compléter le tableau :
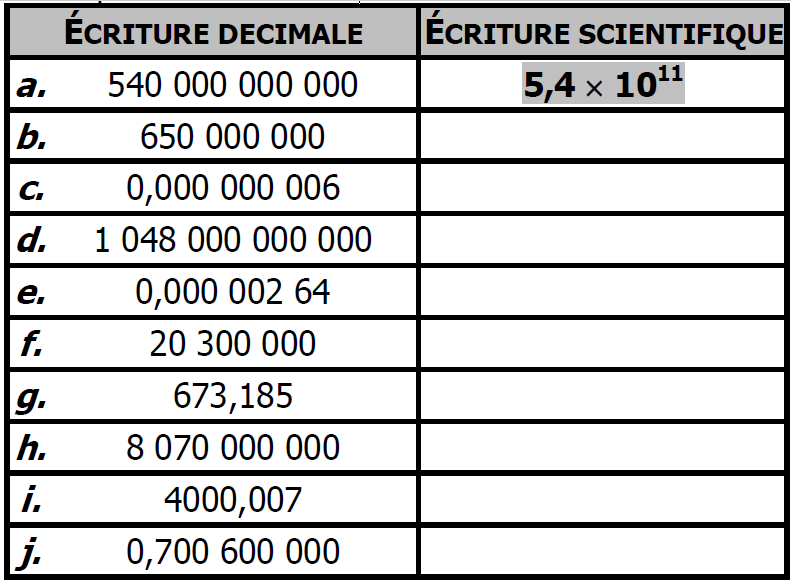
$2)$ Compléter le tableau :
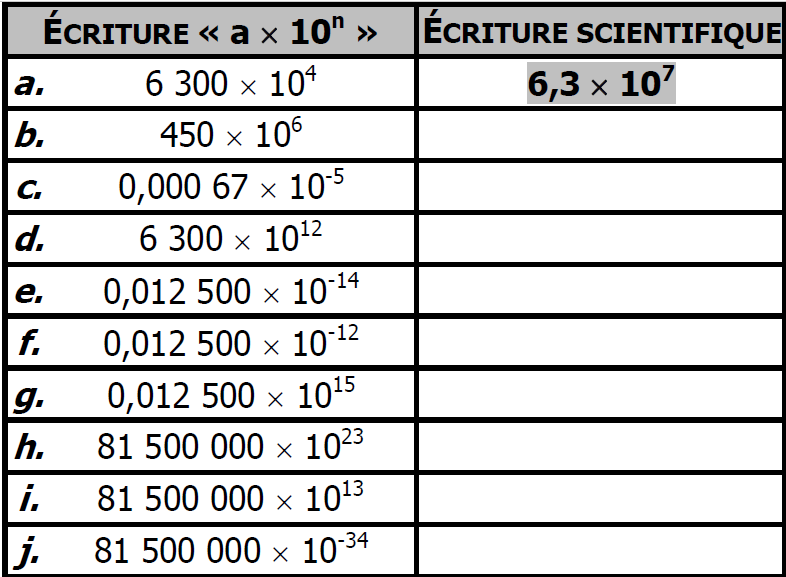
$1)$ Compléter le tableau :
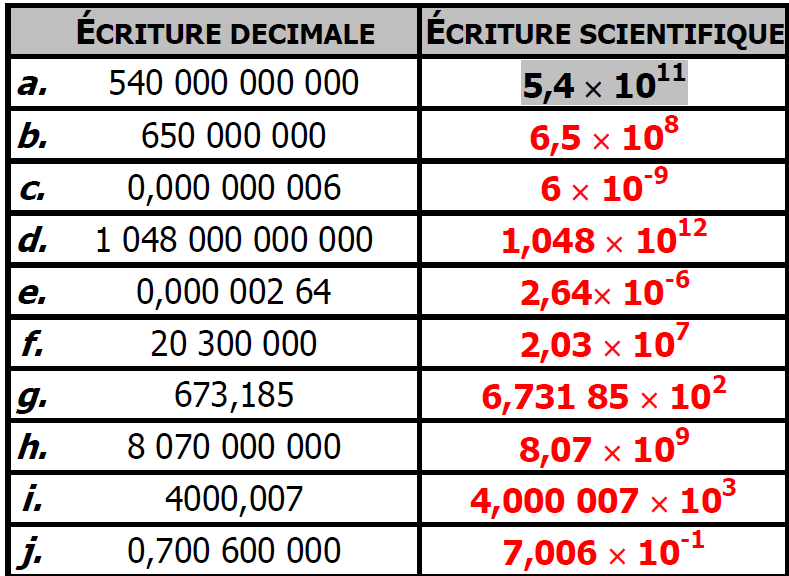
$2)$ Compléter le tableau :
Exercice 15:
$1)$ Comparer ces nombres en écriture scientifique :
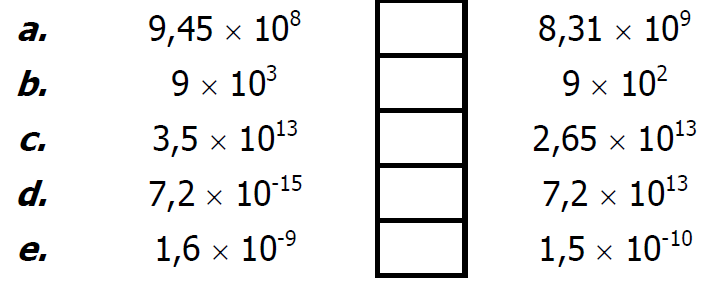
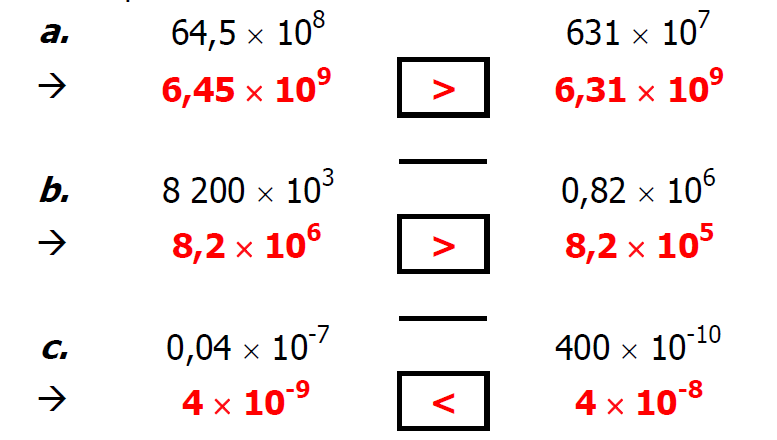
$2)$ Donner l’écriture scientifique des deux nombres puis les comparer :
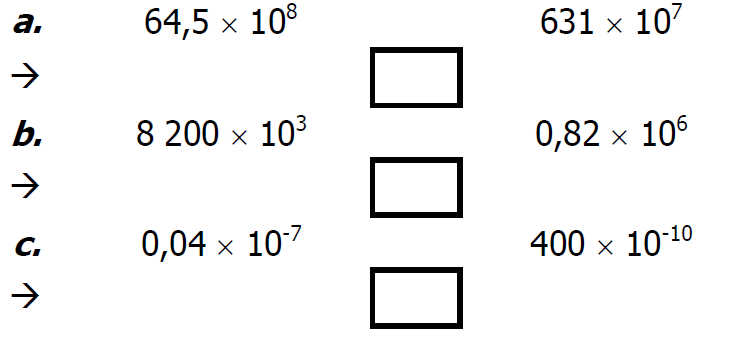
$1)$ Comparer ces nombres en écriture scientifique :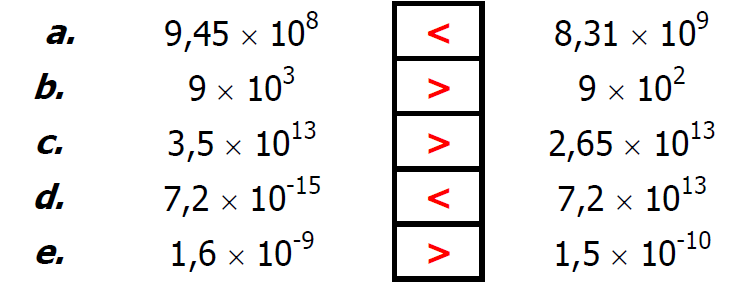
$2)$ Donner l’écriture scientifique des deux nombres puis les comparer :
Puissances exercices corrigés 1AC