La réciproque du théorème de Thalès est une propriété géométrique qui permet de déduire la parallélisme de deux droites à partir d’une condition de rapport de longueurs de segments. Cette propriété est souvent utilisée dans des problèmes de géométrie où l’on doit déterminer si certaines droites sont parallèles.
Voici comment la réciproque du théorème de Thalès peut être énoncée de manière plus détaillée :
1- Réciproque de Thalès :
La réciproque du théorème de Thalès, également connue sous le nom de théorème de la réciproque de Thalès, présente les propriétés suivantes :

2. Résumé de la réciproque de Thalès
La réciproque du théorème de Thalès énonce que si dans un triangle, une droite parallèle à l’un des côtés coupe les deux autres côtés en des points tels que les rapports des longueurs des segments de part et d’autre de la droite parallèle sont égaux.
Alors cette droite est parallèle au côté initial. En d’autres termes, si les rapports des longueurs des segments sont égaux, les droites sont parallèles.
Cela se base sur la similarité des triangles formés et la conservation des angles correspondants.
C’est un outil clé pour prouver la parallélisme des droites dans des problèmes géométriques.
3. Exemple:
voici un exemple concret de la réciproque du théorème de Thalès :
Considérons un triangle ABC, où AB est la base et AC est un côté incliné. Soit D un point sur AB et E un point sur AC tels que la droite DE soit parallèle à BC.
Selon la réciproque du théorème de Thalès, si les rapports des longueurs des segments AD/DB et AE/EC sont égaux, alors la droite DE est parallèle à BC.
Données :
– Triangle ABC où A, B et C sont les sommets.
– La droite DE est parallèle à BC.
– D est un point sur AB et E est un point sur AC.À prouver :
La droite DE est parallèle à BC.
Conditions :
- Si AD/DB = AE/EC
Démonstration :
Par la réciproque de Thalès, les rapports égaux AD/DB et AE/EC impliquent que les triangles ADE et BDE sont semblables, ainsi que les triangles AED et CED.
En conséquence des triangles semblables, les angles correspondants sont égaux : ∠ADE = ∠BDE et ∠AED = ∠CED.
Étant donné que DE est une ligne droite, les angles ∠ADE et ∠AED sont complémentaires (leur somme vaut 180 degrés).
De même, les angles ∠BDE et ∠CED sont complémentaires.
Puisque les angles ∠ADE et ∠BDE sont égaux et que les angles ∠ADE et ∠AED sont complémentaires, il s’ensuit que les angles ∠BDE et ∠AED sont complémentaires.
Cependant, deux angles complémentaires ne peuvent pas être égaux. Par conséquent, ∠BDE ≠ ∠AED.
Cette contradiction indique que les hypothèses sont fausses, c’est-à-dire que AD/DB ≠ AE/EC.
Par conséquent, la seule possibilité est que DE est effectivement parallèle à BC.
Ainsi, cet exemple illustre comment la réciproque du théorème de Thalès peut être utilisée pour prouver la parallélisme d’une droite à l’aide de conditions de rapports de longueurs dans un triangle.
Sur la figure ci-contre, on donne ZN = 4,4 cm, ZR = 14,4 cm, ZJ = 9,9 cm et NB = 2 cm. 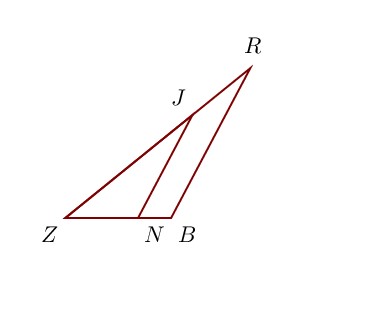
Démontrer que les droites (BR) et (NJ) sont parallèles
Sur la figure ci-contre, on donne CW = 9,1 cm, CX = 5,2 cm, ZX = 2 cm et CQ = 5,6 cm. 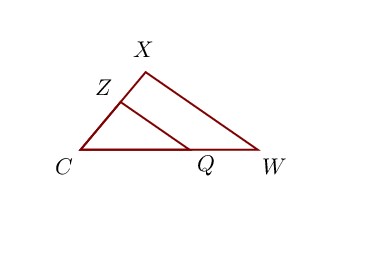
Démontrer que les droites (W X) et (QZ) sont parallèles.
Sur la figure ci-contre, on donne UE = 2,5 cm, BV = 14,7 cm, UV = 11,2 cm et UH = 8 cm. 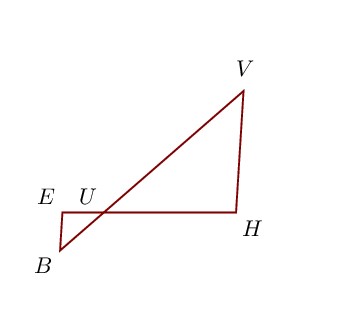
Démontrer que les droites (HV ) et (EB) sont parallèles.
Sur la figure ci-contre, on donne IK = 15,2 cm, W K = 10,4 cm, W L = 3,9 cm et W S = 1,8 cm. 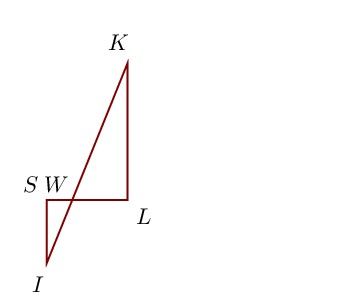
Démontrer que les droites (LK) et (SI) sont parallèles.
Sur la figure ci-contre, on donne QS = 1 cm, W I = 1,8 cm, W N = 3 cm et W S = 2,5 cm. 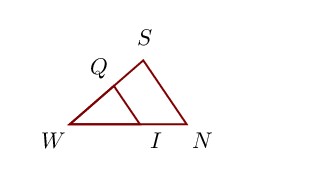
Démontrer que les droites (NS) et (IQ) sont parallèles.





