Repère dans le plan exercices corrigés
Exercice 1:
$1)$ Lire dans ce repère les coordonnées des points $A , B, C, D, E$ et $F $:
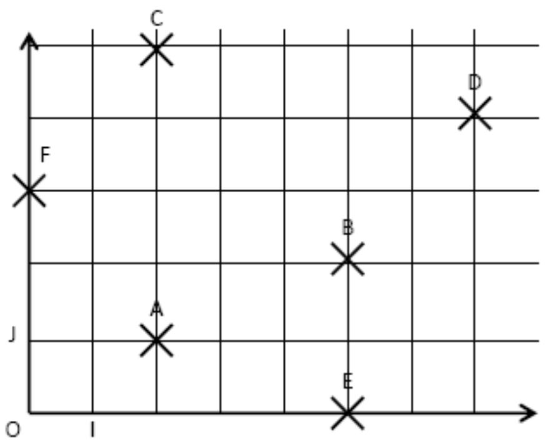
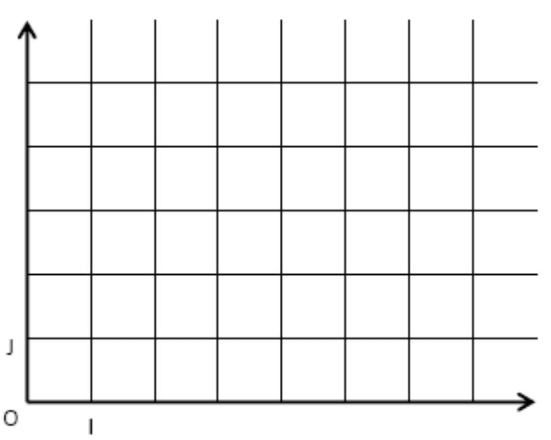
$2)$ Placer dans ce repère les points suivants : $A(3;1)$ ; $B(5 ; 2)$ ; $C(1 ; 3)$ ; $D(7 ; 5)$ ; $E(4 ; 0)$ ; $F(0; 5)$
$1)$
$A(2 ; 1)$
$B(5 ; 2)$
$C(2 ; 5)$
$D(7 ; 4)$
$E(5 ; 0)$
$F(0 ; 3)$
$2)$
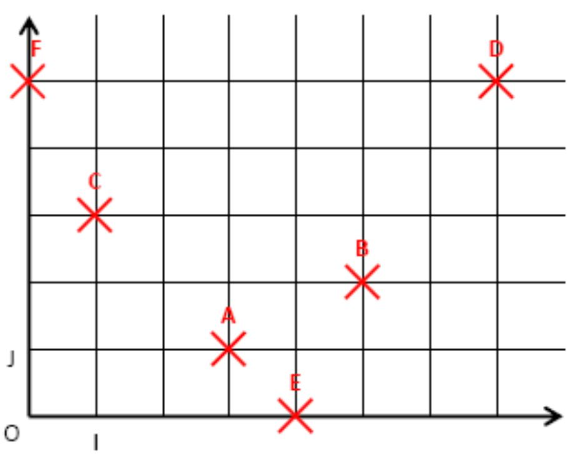
Exercice 2:
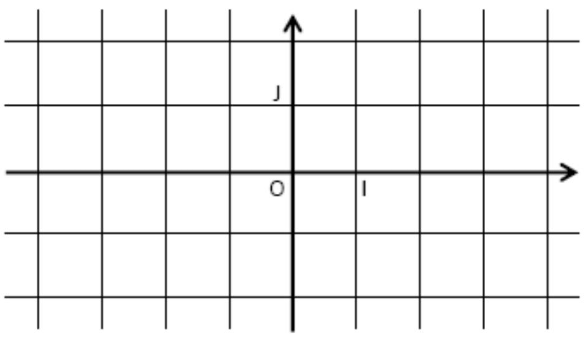
$1)$ Lire dans ce repère les coordonnées des points $G, H, I, J, K$ et $L$:
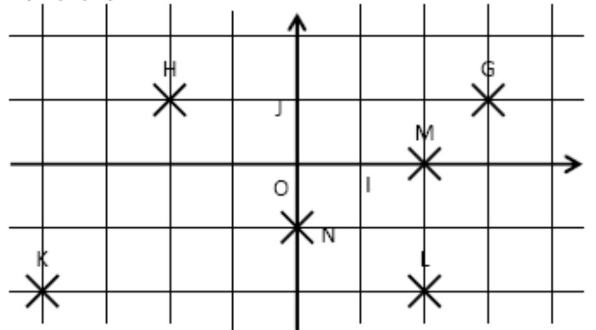
$2)$ Placer dans ce repère les points suivants : $G(3 ; 1)$ ; $H( -2 ; 1 )$ ; $K(-4 ;-2)$ ; $L(0 ;-2)$ ; $M(3 ; 0) $ ; $ N(1,5 ;-2,5)$
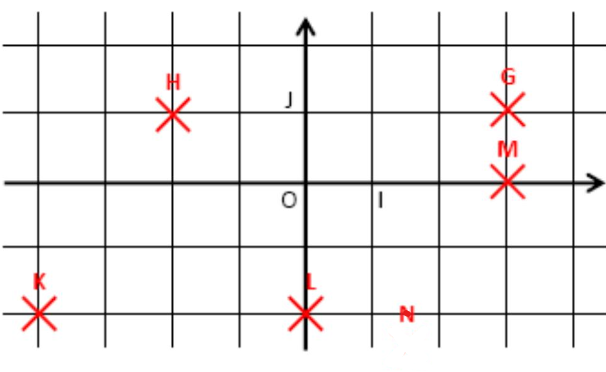
$1)$
$G(3 ; 1)$
$H(-2 ;1)$
$K(-4 ;-2)$
$L(2; -2)$
$M(2 ; 0)$
$N(0 ;-1)$
$2)$
Exercice 3:
Déterminer les coordonnées du point $I$ milieu du segment $[AB]$ dans les cas suivants :
$ 1)$ $ A(1 ;-5) \text { et } B(3 ;-9) $
$ 2)$ $A(-2 ; 1) \text { et } B(2 ; 0)$
$ 3)$ $A(-3 ; \sqrt{2}) \text { et } B(2 ;-\sqrt{2}) $
$ 4)$ $A(1 ;-3) \text { et } B(-1 ; 3)$
$1)$ $x_{I}=\frac{1+3}{2}=2$ et $y_{I}=\frac{-5-9}{2}=-7$
Donc $I(2 ;-7)$
$2)$ $x_{I}=\frac{-2+2}{2}=0$ et $y_{I}=\frac{1+0}{2}=\frac{1}{2}$
Donc $I\left(0 ; \frac{1}{2}\right)$
$3)$ $x_{I}=\frac{-3+2}{2}=-\frac{1}{2}$ et $y_{I}=\frac{\sqrt{2}-\sqrt{2}}{2}=0$.
Donc $I\left(-\frac{1}{2} ; 0\right)$.
$4)$ $x_{I}=\frac{1-1}{2}=0$ et $y_{I}=\frac{-3+3}{2}=0$.
Donc $I(0 ; 0)$ est l’origine du repère.
Exercice 4:
Dans un repère orthonormé $(O,I,J)$ , $OI=OJ=1cm$ on considère les points : $A(-2;-3)$ ; $B(-4;4) $; $C(3 ; 6)$.
• Calculer les coordonnées des vecteurs : $\overrightarrow{AB} $ ; $\overrightarrow{BC} $ et $\overrightarrow{AC} $
$\overrightarrow{A B}\left(x_{B}-x_{A} ; y_{B}-y_{A}\right)$
$\overrightarrow{A B}(-4+2 ; 4+3)$
$\overrightarrow{A B}(-2 ; 7)$
$\overrightarrow{B C}\left(x_{C}-x_{B} ; y_{C}-y_{B}\right)$
$\overrightarrow{B C}(3+4 ; 6+3)$
$\overrightarrow{B C}(7 ; 9)$
$\overrightarrow{A C}\left(x_{C}-x_{A} ; y_{C}-y_{A}\right)$
$\overrightarrow{A C}(3+2 ; 6+3)$
$\overrightarrow{A C}(5 ; 9)$
Exercice 5:
Le repère est orthonormé.
Déterminer dans chacun des cas les distances $ AB, AC$ et $ BC$ . Le triangle $ABC$ est-il rectangle?
$1)$ $ A(3;0), B(−1;0), C(−1;3)$
$2)$ $ A(−2;3), B(3;2), C(0;0)$
$3)$ $ A(0;5), B(3;6), C(5;-2)$
$1)$ $A B^{2}=\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}=(-1-3)^{2}+(0-0)^{2}=16$
$A B=\sqrt{16}=4$
$A C^{2}=(-1-3)^{2}+(3-0)^{2}=(-4)^{2}+3^{2}=25$
$A C=\sqrt{25}=5$
$B C^{2}=(-1+1)^{2}+(3-0)^{2}=0^{2}+3^{2}=9$
$B C=\sqrt{9}=3$
Dans le triangle $A B C$, le plus grand côté est $[A C]$.
D’une part $A C^{2}=25$
D’autre part $A B^{2}+B C^{2}=9+16=25$
Par conséquent $A C^{2}=A B^{2}+B C^{2}$
D’après la réciproque du théorème de Pythagore, le triangle $A B C$ est rectangle en $B$.
$2)$$A B^{2}=\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}=(3+2)^{2}+(2-3)^{2}=5^{2}+(-1)^{2}=25+1=26$
$A B=\sqrt{26}$
$A C^{2}=(0+2)^{2}+(0-3)^{2}=2^{2}+(-3)^{2}=4+9=13$
$A C=\sqrt{13}$
$B C^{2}=(0-3)^{2}+(0-2)^{2}=(-3)^{2}+(-2)^{2}=9+4=13$
$B C=\sqrt{13}$
Dans le triangle $A B C$, le plus grand côté est $[A B]$.
D’une part $A B^{2}=26$
D’autre part $A C^{2}+B C^{2}=13+13$.
Par conséquent $A B^{2}=A C^{2}+B C^{2}$.
D’après la réciproque du théorème de Pythagore, le triangle $A B C$ est rectangle en $C$. De plus $A C=B C$.
Le triangle est donc rectangle isocèle en $C$.
$3)$ $A B^{2}=\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}=(3+2)^{2}+(2-3)^{2}=(3-0)^{2}+(6-5)^{2} $
$=3^{2}+1^{2}=10 $
$A B=\sqrt{10} $
$A C^{2}=(5-0)^{2}+(-2-5)^{2}=5^{2}+(-7)^{2}=25+49=74 $
$A C=\sqrt{74} $
$B C^{2}=(5-3)^{2}+(-2-6)^{2}=2^{2}+(-8)^{2}=4+64=68 $
$B C=\sqrt{68}$
Dans le triangle $A B C$ le plus grand côté est $[A C]$.
D’une part $A C^{2}=74$
D’autre part $A B^{2}+B C^{2}=10+68=78$
Par conséquent $A C^{2} \neq A B^{2}+B C^{2}$.
D’après la contraposée du théorème de Pythagore, le triangle $A B C$ n’est pas rectangle.
Exercice 6:
Dans un repère orthonormé, on donne les points $A(3;7), B(−3;1)$ et $C(1;−3)$.
• Démontrer que le triangle $ABC$ est un triangle rectangle. Est-il isocèle? Justifier.
$ A B^{2}=\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}=(-3-3)^{2}+(1-7)^{2}=(-6)^{2}+(-6)^{2}=72 $
$ A C^{2}=(1-3)^{2}+(-3-7)^{2}=(-2)^{2}+(-10)^{2}=104 $
$ B C^{2}=(1+3)^{2}+(-3-1)^{2}=4^{2}+(-4)^{2}=32$
Dans le triangle $A B C,[A C]$ est le plus grand côté.
D’une part $A C^{2}=104$.
D’autre part $A B^{2}+B C^{2}=72+32=104$
Par conséquent $A C^{2}=A B^{2}+B C^{2}$.
D’après la réciproque du théorème de Pythagore, le triangle $A B C$ est rectangle en $B$.
Mais $B C \neq A B$. Le triangle $A B C$ n’est donc pas isocèle.
Exercice 7:
Dans un repère du plan, on considère les points $E(3;4), F(6;6)$ et $G(4;−1)$.
• Calculer les coordonnées du point $H$ tels que $EFGH$ soit un parallélogramme.
On appelle $K$ le milieu de $[E G]$.
$\left\{\begin{array}{l}{ x _ { K } = \frac { x _ { E } + x _ { G } } { 2 } } \\ { y _ { K } = \frac { y _ { E } + y _ { G } } { 2 } }\end{array}\right.$
$\left\{\begin{array}{l}x_{K}=\frac{3+4}{2} \\ y_{K}=\frac{4+(-1)}{2}\end{array}\right.$
$\left\{\begin{array}{l}x_{K}=\frac{7}{2} \\ y_{K}=\frac{3}{2}\end{array}\right.$
Les diagonales d’un parallélogramme se coupent en leur milieu. $K$ est donc également le milieu de $[F H]$.
$\left\{\begin{array}{l}{ x _ { K } = \frac { x _ { F } + x _ { H } } { 2 } } \\ { y _ { K } = \frac { y _ { F } + y _ { H } } { 2 } }\end{array}\right.$
$\left\{\begin{array}{l}\frac{7}{2}=\frac{6+x_{H}}{2}\\ \frac{3}{2}=\frac{6+y_{H}}{2}\end{array}\right.$
On multiplie chacune des équations par 2 (les deux côtés!) afin de ne plus avoir de dénominateur:
$\left\{\begin{array}{l}7=6+x_{H} \\ 3=6+y_{H}\end{array}\right.$
Finalement $\left\{\begin{array}{l}x_{H}=1 \\ y_{H}=-3\end{array}\right.$
Donc $H(1 ;-3)$
Exercice 8:
Dans le repère orthonormé $(O;I,J)$ du plan, on considère les points $A(−2;−3)$ et $B(4;1)$.
• Les points $M(3;2)$ et $N(−2 ; \frac{5}{2})$ sont-ils sur le cercle de diamètre $[AB]$? Justifier.
Un point est sur un cercle donné si la distance le séparant du centre du cercle est égale au rayon du cercle. Déterminons dans un premier temps les coordonnées du centre $I$ du cercle. Il s’agit du milieu de $[A B]$.
$\left\{\begin{array}{l}x_{I}=\frac{x_{A}+x_{B}}{2}=\frac{-2+4}{2}=1 \\ y_{I}=\frac{y_{A}+y_{B}}{2}=\frac{-3+1}{2}=-1\end{array}\right.$
$I$ a donc pour coordonnées $(1 ;-1)$
Le rayon du cercle est $O A$.
$O A^{2}=\left(x_{A}-x_{O}\right)^{2}+\left(y_{A}-y_{O}\right)^{2}=(-2-1)^{2}+(-3+1)^{2}=(-3)^{2}+(-2)^{2}=9+4=13$
Donc $O A=\sqrt{13}$.
Calculons maintenant $O M$
$O M^{2}=(3-1)^{2}+(2+1)^{2}=2^{2}+3^{2}=4+9=13$
Donc $O M=\sqrt{13}=O A$. Le point $M$ appartient au cercle de diamètre $[A B]$
Calculons enfin $O N$
$O N^{2}=(-2-1)^{2}+\left(\frac{5}{2}+1\right)^{2}=(-3)^{2}+\left(\frac{7}{2}\right)^{2}=\frac{85}{4}$
Donc $O N=\sqrt{\frac{85}{4}} \neq O A$. Le point $N$ n’appartient pas au cercle de diamètre $[A B]$.
Exercice 9:
Dans un repère orthonormé du plan, on considère les points $A(4;1), B(0;4)$ et $C(−6;−4)$.
$1)$ Calculer $AB, AC$ et $BC$.
$2)$ En déduire que le triangle $ABC$ est rectangle.
$3)$ Trouver ensuite les coordonnées du centre du cercle circonscrit à ce triangle. Quel est son rayon?
$1)$ $A B^{2}=(0-4)^{2}+(4-1)^{2}=(-4)^{2}+3^{2}=25$.
Donc $A B=5$
$A C^{2}=(-6-4)^{2}+(-4-1)^{2}=(-10)^{2}+(-5)^{2}=125$.
Donc $A C=\sqrt{125}=5 \sqrt{5}$
$B C^{2}=(-6-0)^{2}+(-4-4)^{2}=(-6)^{2}+(-8)^{2}=100$.
Donc $B C=10$.
$2)$ Dans le triangle $A B C,[A C]$ est le plus grand côté.
D’une part $A C^{2}=125$
D’autre part $A B^{2}+B C^{2}=25+100=125$
Donc $A C^{2}=A B^{2}+B C^{2}$.
D’après la réciproque du théorème de Pythagore, le triangle $A B C$ est rectangle en $B$.
$3)$ Le centre $I$ du cercle circonscrit est donc le milieu de l’hypoténuse $[A C]$.
On a ainsi $\left\{\begin{array}{l}x_{I}=\frac{x_{A}+x_{C}}{2}=\frac{4-6}{2}=-1 \\ y_{I}=\frac{y_{A}+y_{C}}{2}=\frac{1-4}{2}=-\frac{3}{2}\end{array}\right.$
Par conséquent $I\left(-1 ;-\frac{3}{2}\right)$
Le rayon du cercle est donc $\frac{A C}{2}=\frac{5 \sqrt{5}}{2}$
Exercice 10:
Dans le plan muni d’un repère orthonormé $(O;I,J)$ on considère les points $A(−3;0), B(2;1), C(4;3)$ et $D(−1;2)$.
$1)$ Placer les points $A, B, C$ et $D$.
$2)$ Démontrer que les segments $[AC]$ et $[BD]$ ont le même milieu $K$.
$3)$ Montrer que le triangle $OBD$ est rectangle est isocèle.
$4)$ On considère le point $E$ du plan tel que $BODE$ soit un parallélogramme.
Quelles sont les coordonnées de $E$.
$5)$ Calculer $AE$.
$1)$
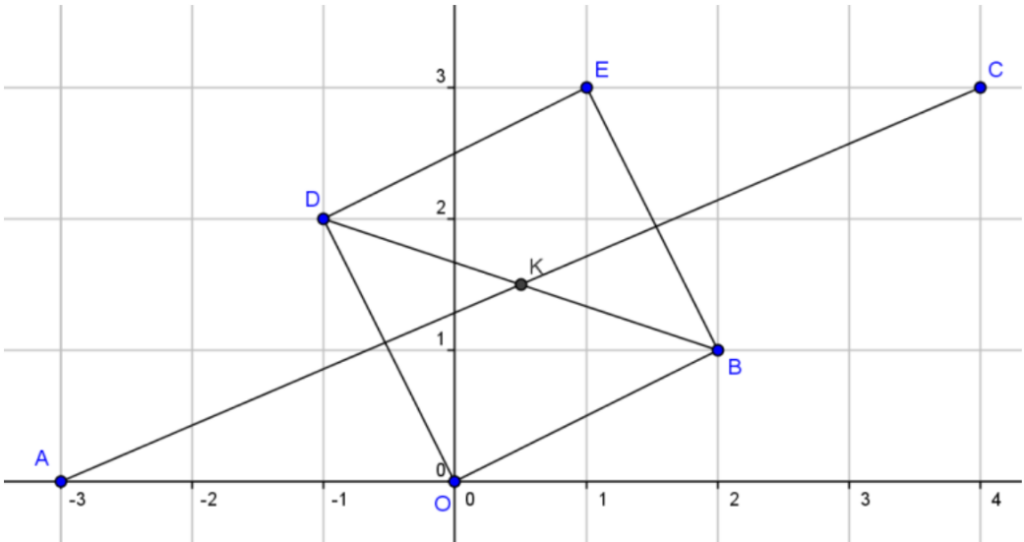
$2)$ Soit $K$ le milieu de $[A C]$.
On a ainsi $\left\{\begin{array}{l}x_{K}=\frac{-3+4}{2}=\frac{1}{2} \\ y_{K}=\frac{0+3}{2}=\frac{3}{2}\end{array}\right.$
Soit $K^{\prime}$ le milieu de $[B D]$.
On a ainsi $\left\{\begin{array}{l}x_{K^{\prime}}=\frac{2-1}{2}=\frac{1}{2} \\ y_{K^{\prime}}=\frac{1+2}{2}=\frac{3}{2}\end{array}\right.$
Par conséquent $K$ et $K^{\prime}$ sont ayant les mêmes coordonnées sont confondus et les segments $[A C]$ et $[B D]$ ont le même milieu.
$3)$ Calculons les longueurs $O B, O D$ et $B D$.
$O B^{2}=(2-0)^{+}(1-0)=5$ donc $O B=\sqrt{5}$
$O D^{2}=(-1-0)^{2}+(2-0)^{2}=5$
Donc $O D=\sqrt{5}$. Le triangle $O B D$ est donc isocèle en $O$.
$B D^{2}=(-1-2)^{2}+(2-1)^{2}=(-3)^{2}+1^{2}=10$
Donc $B D=\sqrt{10}$.
Dans le triangle $O B D$, le plus grand côté est $[B D]$.
D’une part $B D^{2}=10$
D’autre part $O B^{2}+O D^{2}=5+5=10$
Par conséquent $B D^{2}=O B^{2}+O D^{2}$ et d’après la réciproque du théorème de Pythagore, le triangle $O B D$ est également rectangle en $O$.
$4)$ $B O D E$ est un parallélogramme, par conséquent ses diagonales $[B D]$ et $[O E]$ se coupent en leur milieu $K$.
On obtient ainsi :
$\left\{\begin{array}{l}{ x _ { K } = \frac { x _ { O } + x _ { E } } { 2 } } \\ { y _ { K } = \frac { y _ { O } + y _ { E } } { 2 } }\end{array}\right.$
$\left\{\begin{array}{l}\frac{1}{2}=\frac{0+x_{E}}{2} \\ \frac{3}{2}=\frac{0+y_{E}}{2}\end{array}\right.$
Finalement $E(1 ; 3)$.
$5)$ $A E^{2}=(1+3)^{2}+(3-0)^{2}=4^{2}+3^{2}=25$ donc $A E=5$.
Exercice 11:
Dans un repère orthonormé $(O;I,J)$ on considère les points $A(1;−1), B(−2;0)$ et $C(−1;3)$.
$1)$ Quelle est la nature du triangle $ABC$? Justifier.
$2)$ Déterminer les coordonnées du point $D$ symétrique du point $B$ par rapport au point $A$.
$3)$ Déterminer les coordonnées du point $E$ tel que $ECAB$ soit un parallélogramme.
$1)$ On calcule les longueurs des trois côtés du triangle.
$A B=\sqrt{(-2-1)^{2}+(0+1)^{2}}=\sqrt{10}$
$B C=\sqrt{(-1+2)^{2}+(3-0)^{2}}=\sqrt{10}$
$A C=\sqrt{(-1-1)^{2}+(3+1)^{2}}=\sqrt{20}$
On constate que $A B=B C$. Le triangle $A B C$ est donc isocèle en $B$.
On constate également que $A B^{2}+B C^{2}=10+10=20=A C^{2}$.
D’après la réciproque du théorème de Pythagore, le triangle $A B C$ est également rectangle en $B$.
$2)$ Le point $A$ est donc le milieu du segment $[B D]$
Ainsi $x_{A}=\frac{x_{B}+x_{D}}{2} \Leftrightarrow 1=\frac{-2+x_{D}}{2} \Leftrightarrow 2=x D-2 \Leftrightarrow x_{D}=4$
et $y_{A}=\frac{y_{B}+y_{D}}{2} \Leftrightarrow-1=\frac{0+y_{D}}{2} \Leftrightarrow-2=y D$
Par conséquent $D(4 ;-2)$.
$3)$ On appelle $M$ le milieu du segment $[B C]$
Ainsi $x_{M}=\frac{-2-1}{2}=-\frac{3}{2}$ et $y_{M}=\frac{0+3}{2}=\frac{3}{2}$.
$E C A B$ est un parallélogramme. Ses diagonales se coupent donc en leur milieu. $M$ est donc également le milieu du segment $[E A]$.
Par conséquent :
$-\frac{3}{2}=\frac{x_{E}+1}{2} \Leftrightarrow-3=x_{E}+1 \Leftrightarrow x_{E}=-4$
$\frac{3}{2}=\frac{y_{E}-1}{2} \Leftrightarrow 3=y_{E}-1 \Leftrightarrow y_{E}=4$.
Ainsi $E(-4 ; 4)$.
Exercice 12:
$1)$ Déterminer les coordonnées des points $A, B, C, O, I$ et $J$
$2)$ Déterminer les coordonnées de $\overrightarrow{O I}$ et $\overrightarrow{O J}$, et calculer $O I$ et $\boldsymbol{O J}$
$3)$ Montrer que le point $O(0 ; \mathbf{0})$ est milieu du segment $[AC]$
$4)$ Déterminer les coordonnées de $\boldsymbol{D}$ symétrique de $\boldsymbol{B}$ par rapport à $\boldsymbol{O}$
$5)$ Déterminer la nature de quadrilatère $A B C D$
$6)$ Déterminer les coordonnées de $M$ l’image de $C$ par le déplacement dont le vecteur $\overrightarrow{O B}$
$7)$ Montrer que le quadrilatère $BMCO$ est un parallélogramme.
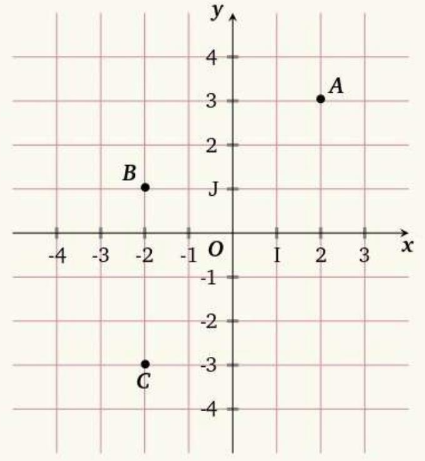
$1)$ Déterminer les coordonnées des points $A, B, C, O, I$ et $J$.
$O(0 ; 0) \quad I(1 ; 0) \quad J(0 ; 1) A(2 ; 3) \quad B(-2 ; 1) \quad C(-2 ;-3)$
$2)$ Déterminer les coordonnées des vecteurs $\overrightarrow{O I}$ et $\overrightarrow{O J}$, et calculer $O I$ et $O J$
On a :$ \overrightarrow{O I}\left(x_{I}-x_{0} ; y_{I}-y_{o}\right) \text { et } \overrightarrow{O J}\left(x_{J}-x_{O} ; y_{J}-y_{o}\right) $
$\overrightarrow{O I}(1-0 ; 0-0) \text { et } \overrightarrow{O J}(0-0 ; 1-0) $
$\overrightarrow{O I}(1 ; 0) \text { et } \overrightarrow{O J}(0 ; 1)$
Donc :
$ O I=\sqrt{1^{2}+0^{2}}=\sqrt{1}=1 $
$ O J=\sqrt{0^{2}+1^{2}}=\sqrt{1}=1$

$3)$ Montrer que $\mathbf{O}(\mathbf{0} ; \mathbf{0})$ est le milieu du segment [AC]
On a : $\quad x_{O}=\frac{x_{A}+x_{C}}{2}=\frac{2+(-2)}{2}=0$ et $y_{O}=\frac{y_{A}+y_{C}}{2}=\frac{3+(-3)}{2}=0$
Donc $\mathbf{O}(\mathbf{0} ; \mathbf{0})$ est le milieu du segment [ $A C$ ]
$4)$ Déterminer les coordonnées du point $D$ symétrique de $B$ par rapport au point $O$.
$D$ symétrique de $\boldsymbol{B}$ par rapport au point $\boldsymbol{O}$ alors $\boldsymbol{O}$ est le milieu du segment $[BD]$
On a $\quad x_{O}=\frac{x_{B}+x_{D}}{2}$ et $y_{O}=\frac{y_{B}+y_{D}}{2}$
$2 x_{O}=x_{B}+x_{D} \text { et } 2 y_{O}=y_{B}+y_{D}$
$2 \times 0=-2+x_{D} \text { et } 2 \times 0=1+y_{D} $
$0+2=x_{D} \text { et } 0-1=y_{D} $
$x_{D}=2 \text { et } y_{D}=-1$
Donc $\quad {D(2 ;-1)}$
Exercice 13:
Dans un repère orthonormé $(\mathrm{O}, \mathrm{I}, \mathrm{J}) \mathrm{OI}=\mathrm{OJ}=1 \mathrm{~cm}$ on considère les points : $\mathrm{A}(-2 ;-3) ; \mathrm{B}(-4 ; 4) ; \mathrm{C}(3 ; 6)$.
$1)$ Faire un figure que l’on complêtera tout au long du problème.
$2)$ Calculer les coordonnées des vecteurs $\overrightarrow{A B} \quad \overrightarrow{B C} \quad \overrightarrow{A C}$
$3)$ Calculer $AB ; BC ; AC$ , Quelle est la nature du triangle $ABC$ ? Pourquoi?
$4)$ Soit $D$ le point tel que $A B C D$ soit un parallélogramme. Calculer les coordonnées de $D$ .
• Quelle est la nature de $ABCD$ ? Pourquoi ?
$5)$ Montrez que le triangle est inscrit dans un cercle dont on précisera le centre et le rayon.
$6)$ Montrez que $D$ appartient au cercle.
$7)$ Soit $E$ l’image de $C$ par la translation de vecteur $\overrightarrow{A B}$
• Calculer les coordonnées de $E$
$8)$ Quelle est la nature du quadrilatère $ABEC $? Pourquoi?
$9)$ Calculez l’aire de $ABEC$ ?
$1)$

$2)$
$\overrightarrow{A B}\left(x_{B}-x_{A} ; y_{B}-y_{A}\right)$
$\overrightarrow{A B}(-4+2 ; 4+3)$
$\overrightarrow{A B}(-2 ; 7)$
$\overrightarrow{B C}\left(x_{C}-x_{B} ; y_{C}-y_{B}\right)$
$\overrightarrow{B C}(3+4 ; 6+3)$
$\overrightarrow{B C}(7 ; 9)$
$\overrightarrow{A C}\left(x_{C}-x_{A} ; y_{C}-y_{A}\right)$
$\overrightarrow{A C}(3+2 ; 6+3)$
$\overrightarrow{A C}(5 ; 9)$
$3)$ $A B=\sqrt{(-2)^{2}+(7)^{2}}=\sqrt{4+49}=\sqrt{53}$
$BC=\sqrt{(7)^{2}+(9)^{2}}=\sqrt{49+81}=\sqrt{130}$
$A C=\sqrt{(5)^{2}+(9)^{2}}=\sqrt{25+81}=\sqrt{106}$
Puisque : $A B≠ AC≠BC$ Alors $ABC$ est un traingle quelconque.
$4)$ Soit $\mathrm{D}(x ; y)$ tel que $ABCD$ soit un parallélogramme.
On a :$\overrightarrow{A B}=\overrightarrow{D C}$ (un parallélogramme)
Et puisque : $\overrightarrow{A B}(-2 ; 7) \quad $ et $\quad \overrightarrow{D C}\left(x_{C}-x_{D} ; y_{C}-y_{D}\right) \quad ⇒ \overrightarrow{D C}(3-x ; 6-y)$
Si deux vecteurs sont égaux alors leurs coordonnées sont égales
$3-x=-2$ et $6-y=7$
$$$ -x=-5 \text { et }-y=1 \tag{5;-1}$
$ x=5 \text { et } y=-1$
$\mathrm{D}(5 ; -1)$
• La nature de $ABCD$ .
$ABCD$ est un parallélogramme qui a un angle droit, donc ABCD est un rectangle de plus $BC = AB$.
Donc $ABCD$ est un carré .( si un rectangle a deux cotés consécutifs de meme mesure alors c’est un carré)
$5)$ $ ABC$ est un triangle rectangle en $B$ donc $ABC$ est inscrit dans le cercle de diamètre$[ AC ]$ .
Le rayon du cercle est donc $\frac{\sqrt{106}}{2}$
Le centre du cercle est $M$ le milieu de $[AC]$
Donc $M\left(\frac{x_{A}+x_{C}}{2} ; \frac{y_{A}+y_{C}}{2}\right)$
$M\left(\frac{-2+3}{2} ; \frac{-3+6}{2}\right)$
$ M\left(\frac{1}{2} ; \frac{3}{2}\right) $
$\mathrm{ABC}$ est inscrit dans le cercle de centre $M$ et re rayon $\frac{\sqrt{106}}{2}$
$6)$ Dans un carré les diagonales sont égales et se coupent en leur milieu.
Donc $M A=M D=\frac{\sqrt{106}}{2}$
Donc $\mathrm{D} \in \mathcal{P}\left(\mathrm{M} ; \frac{\sqrt{106}}{2}\right)$
$7)$ Soit $\mathrm{E}(\mathrm{x} ; \mathrm{y})$ l’image de $C $ par la translation de vecteur $\overrightarrow{A B}$
Donc $\overrightarrow{A B}=\overrightarrow{C E} $
$ \overrightarrow{A B}(-2 ; 7) \quad et \quad \overrightarrow{C E}(x-3 ; y-6)$
$\mathrm{x}-3=-2$ et $\mathrm{y}-6=7$
$ \mathrm{x}=-2+3=1$ et $\mathrm{y}=7+6=13$
$ \mathbf{E}(\mathbf{1} ; \mathbf{1 3})$
Repère dans le plan exercices corrigés
