Symétrie axiale exercices corrigés 2AC destiné aux élèves de la deuxième année collège 2AC biof,pour progresser en maths et doper votre niveau.
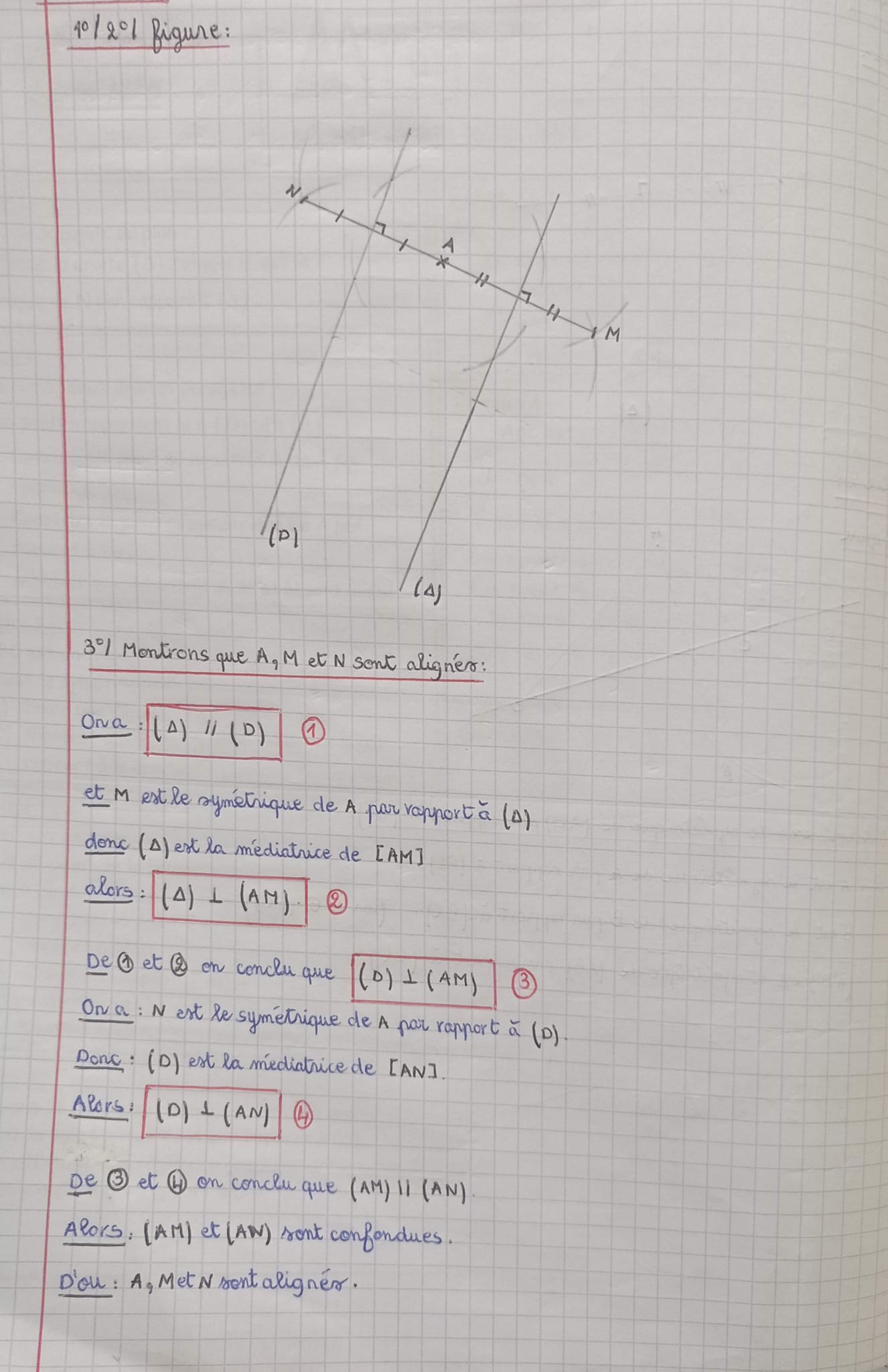
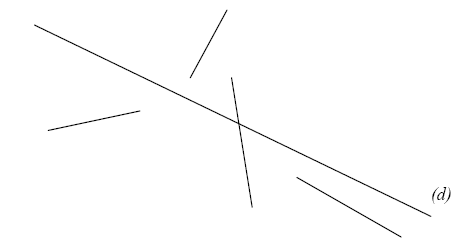
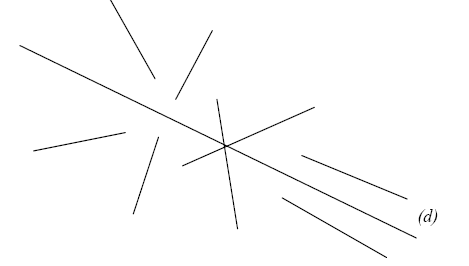
Retrouver, pour chacun de ces dessins, le ou les axes de symétrie.

Retrouver, pour chacun de ces dessins, le ou les axes de symétrie.

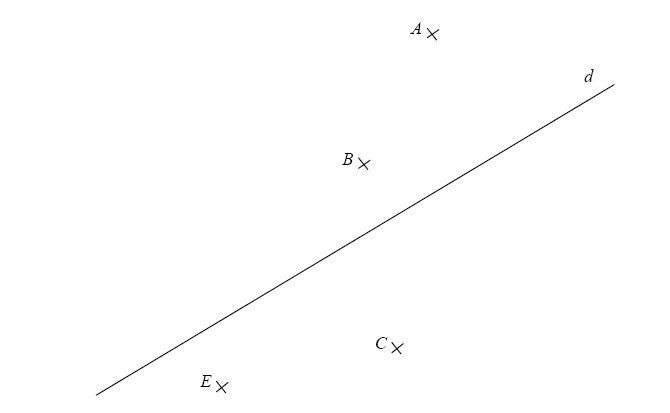
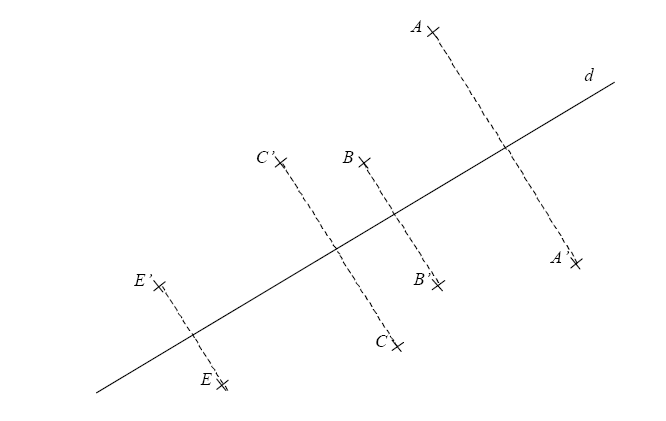
1- Construire avec l’équerre graduée les symétriques des points A, B, C et E par rapport à la droite d.
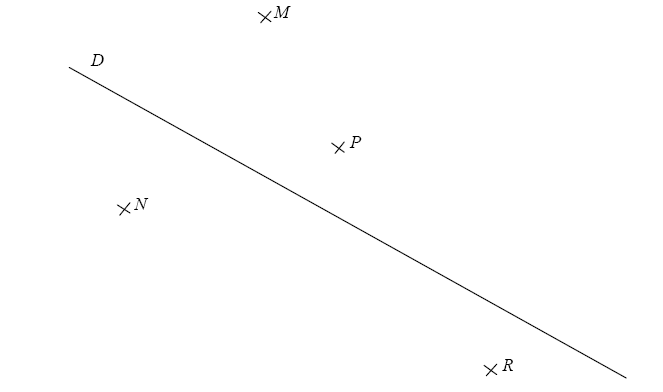
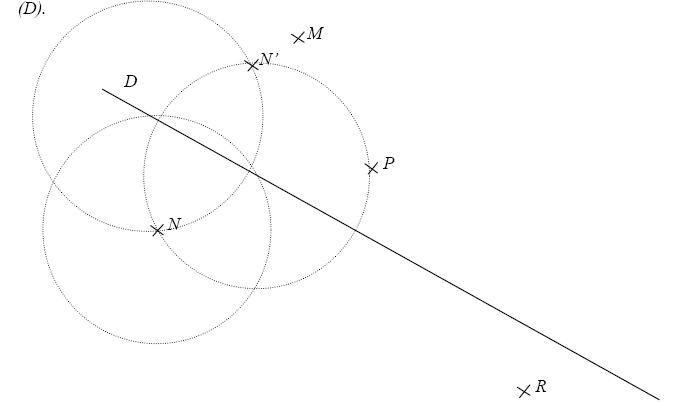
2-Construire avec le compas les symétriques des points M, N , P et R par rapport à la droite (D).
1- Construire avec l’équerre graduée les symétriques des points A, B, C et E par rapport à la droite d.
2-Construire avec le compas les symétriques des points M, N , P et R par rapport à la droite (D).
Construire au compas les symétriques des segments suivants en plaçant les symétriques de leurs extrémités.
Construire au compas les symétriques des segments suivants en plaçant les symétriques de leurs extrémités.
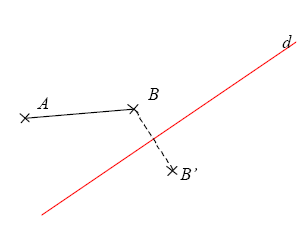
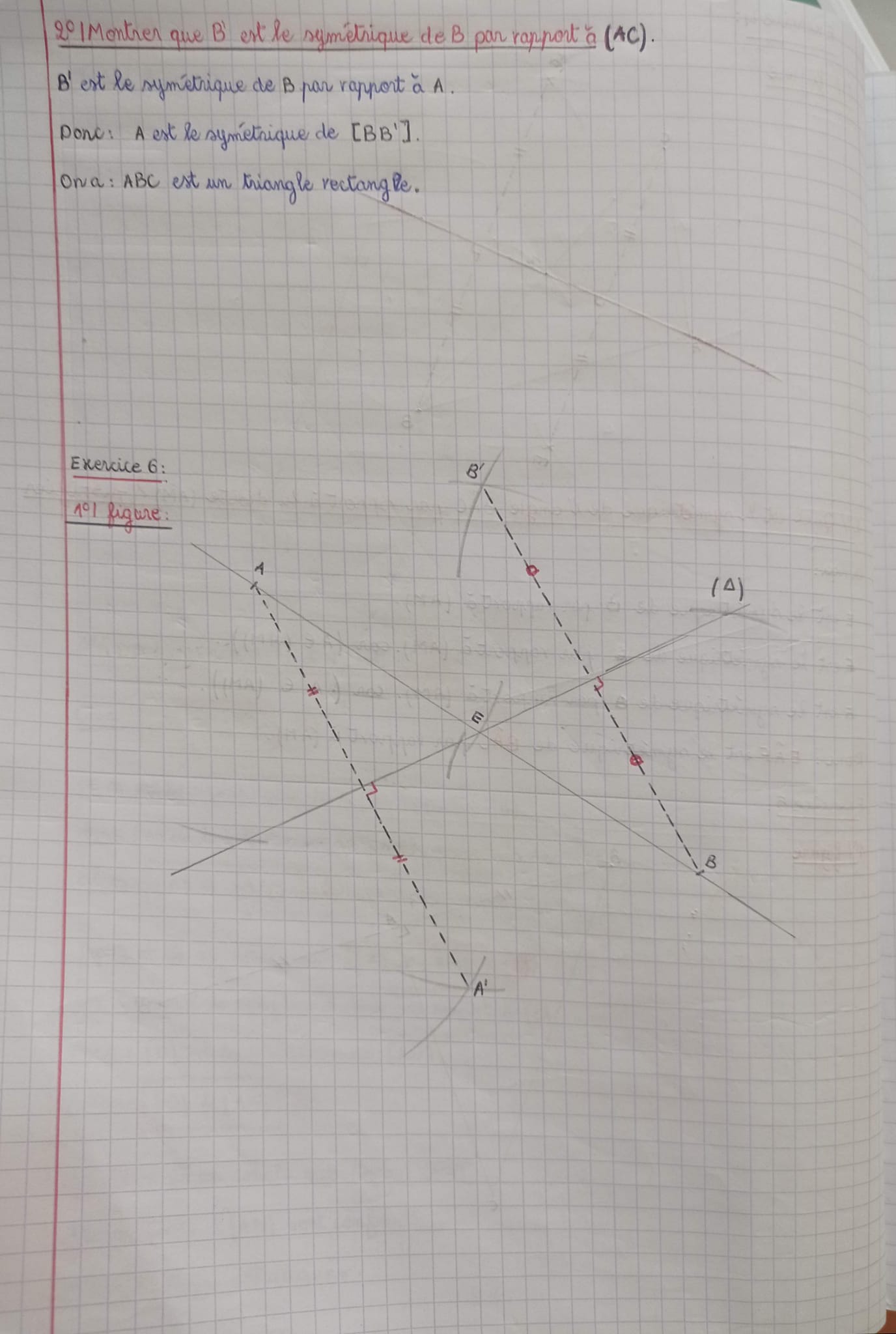
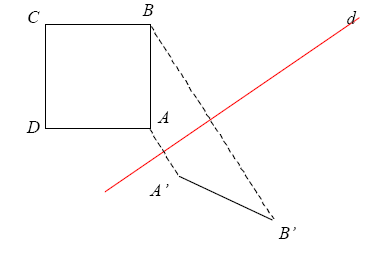
On sait que B et B’ sont symétriques par rapport à d.
On veut construire le symétrique de A en n’utilisant que la règle non graduée et le compas.
Terminer la construction et compléter le texte suivant :
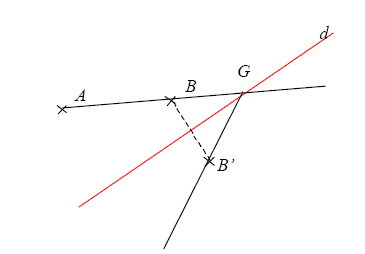
La droite (AB) coupe d en G.
G est son propre symétrique car …………………………………………………………………
La symétrique de (BG) est …………… , car ………………………………………………………
A est un point de (BG), donc A’ est un point de ………, car ……………………………………
……………………………………………………………………………………………………………
Le cercle de centre B’ et de rayon ……… coupe (B’G) en deux points M et N.
A’ est l’un de ces deux points car …………………………………………………………………
On sait que B et B’ sont symétriques par rapport à d.
On veut construire le symétrique de A en n’utilisant que la règle non graduée et le compas.
Terminer la construction et compléter le texte suivant :
La droite (AB) coupe d en G.
G est son propre symétrique car C’est le cas de tout point sur l’axe.
La symétrique de (BG) est (B’G) , car la symétrie conserve l’alignement.
A est un point de (BG), donc A’ est un point de (B’G), car la symétrie conserve l’alignement,
c’est à dire que si un point est sur une droite , son symétrique est sur la symétrique de cette
droite.
Le cercle de centre B’ et de rayon BA coupe (B’G) en deux points M et N.
A’ est l’un de ces deux points car la symétrie conserve les longueurs, et donc la longueur
B’A’ est la même que la longueur AB.
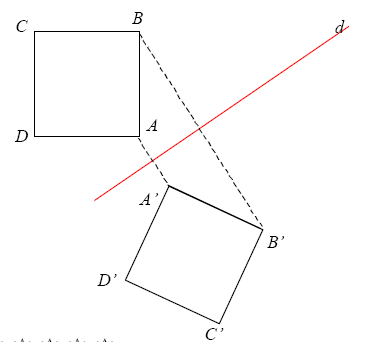
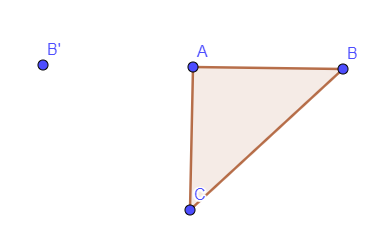
Montrer comment on peut utiliser les propriétés de conservation pour terminer la construction du symétrique d’un carré dès que l’on connaît le symétrique de l’un des côtés.
Pour terminer la construction du symétrique d’un carré .
On sait que (AD) ^ (AB) , la symétrie conserve l’orthogonalité, donc (A’D’) ⊥ (A’B’).
De plus, la symétrie conserve les distances, donc A’D’ = AD.
Pour placer D’, il suffit donc de tracer un segment perpendiculaire et de même longueur que
A’B’.
Et de la même manière, on place C’.
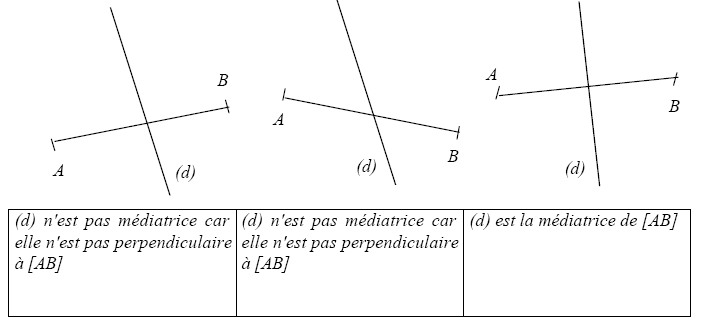
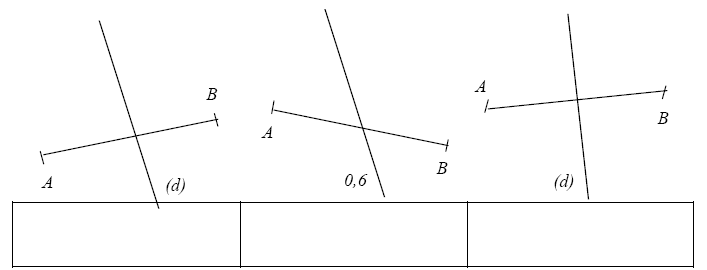
Indiquer dans chaque cas si la droite (d) est la médiatrice du segment [AB] et en donner les raisons. Tracer en rouge la médiatrice lorsque ce n’est pas (d).
1- Tracer deux cercles de même rayon qui se coupent en M et en N.
2-Tracer le segment qui joint les centres A et B de ces deux cercles.
3-Tracer la droite (MN).
4-Que semble représenter la droite (MN) pour le segment [AB]?
5-Que semble représenter la droite (AB) pour le segment [MN]?
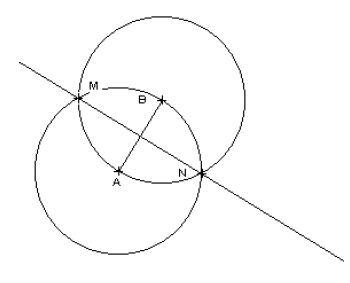
4- (MN) est la médiatrice de [AB].
5-(AB) est la médiatrice de [MN].
1- Tracer un segment [AB] puis sa médiatrice (d).
2-Quel est le symétrique de A par rapport à (d)?
3-Quel est le symétrique de B par rapport à (d)?
4-Placer un point K sur (d) et n’appartenant pas à [AB]. Quel est le symétrique de K par
rapport à (d)?
5-Que peut-on dire des longueurs KA et KB ?
6-Que peut-on dire du triangle BAK?
1-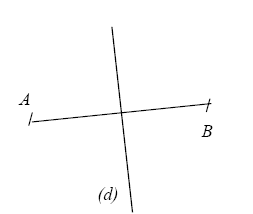
2-Le symétrique de A par rapport à (d) est B.
3-Le symétrique de B par rapport à (d) est A.
4-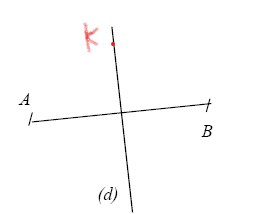
K est son propre symétrique par rapport à (d) (car K appartient à l’axe de symétrie).
5- KA=KB
6-Le triangle BAK est isocèle car AK = BK (longueurs de segments symétriques)
1-Tracer un cercle de centre O et de rayon 4 cm.
2-Tracer un diamètre [AB] de ce cercle.
3-Tracer la médiatrice (D) de [OA], puis tracer le symétrique B’ de B par rapport à (D).
Quelle est la longueur de [BB’]?
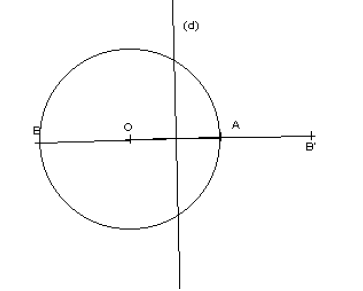
Si I est le milieu de [OA], on a :
OI = IA = 2 cm. et BI = IB’ = 6 cm.
Donc BB’ = 12 cm.
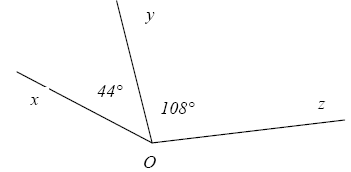
La figure ci-contre est approximative. La reproduire en respectant les mesures qui y sont indiquées.
1- Construire la bissectrice (d) de l’angle ,xôy et la bissectrice (d’) de ,yôz.
2- Mesurer l’angle formé par les droites (d) et (d’)
3- Calculer la moyenne des deux nombres 44 et 108. Conclure.
Les bissectrices de deux angle adjacents forment un angle égal à la moyenne des deux angles initiaux.

2- 76°
3- (44+108)/2 = 76
Refaire le dessin ci-dessous sachant que: ,BÊD = 84 ° et , ,AÊC = 38° La demi-droite [EB) est la bissectrice de l’angle AÊC
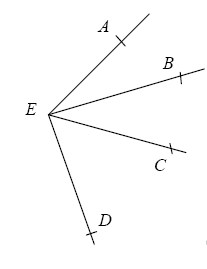
Calculer les mesures en degrés des angles ,CÊD et ,AÊD
BÊC = 38 : 2 = 19°, donc
CÊD = 84 – 19 = 65° ,
AÊD = 84 + 19 = 103°
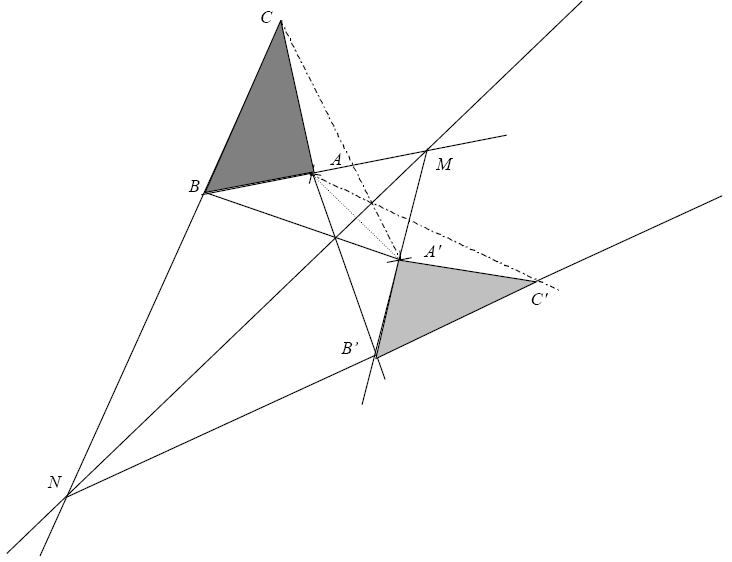
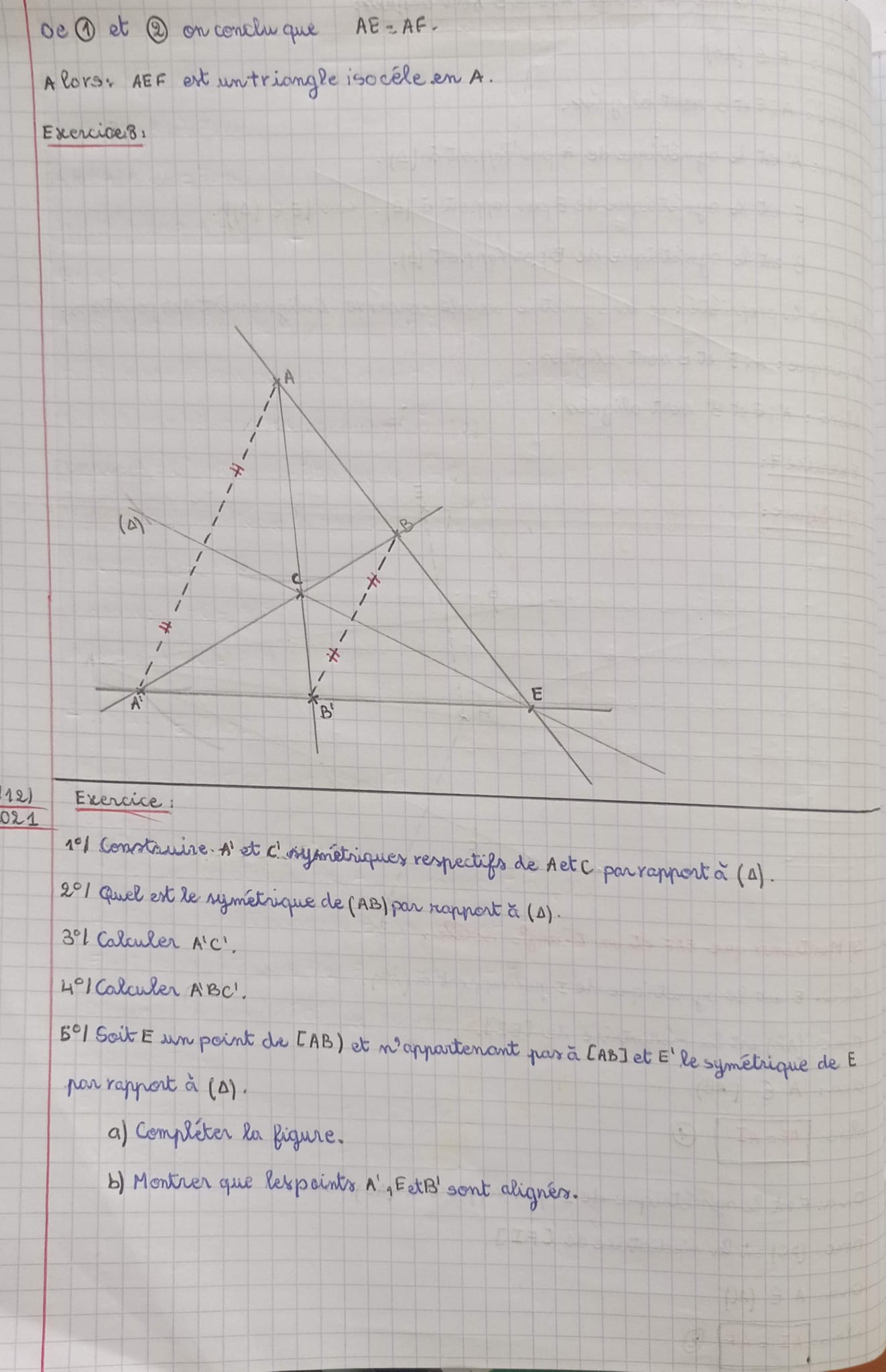
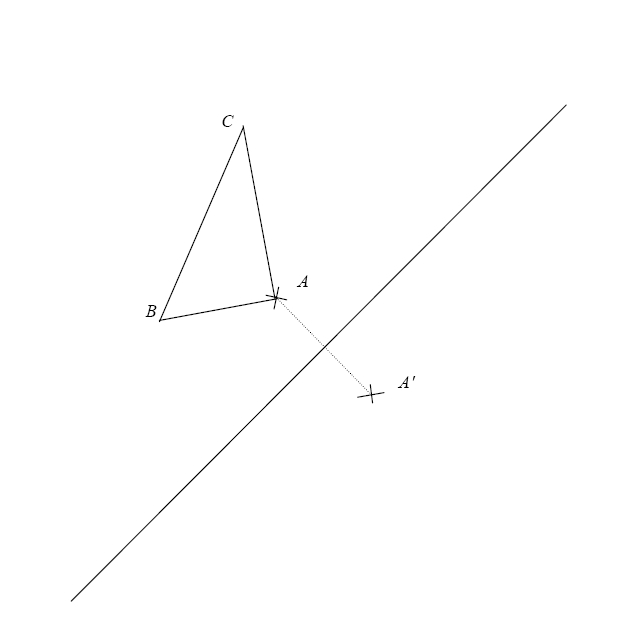
Les deux points A et A’ sont symétriques par rapport à l’axe. Le but est de construire le
symétrique B’ ,C’ de B,C en n’utilisant que la règle non graduée.(c’est à dire que l’on peut
seulement tracer des droites).
On ne peut donc ni mesurer, ni tracer de perpendiculaires.
Les deux constructions des symétriques (à l’équerre, ou au compas) sont ici inopérantes.
On utilise la propriété des droites symétriques sécantes : Si deux droites sont symétriques
et sont sécantes, alors elles se coupent sur l’axe de symétrie.
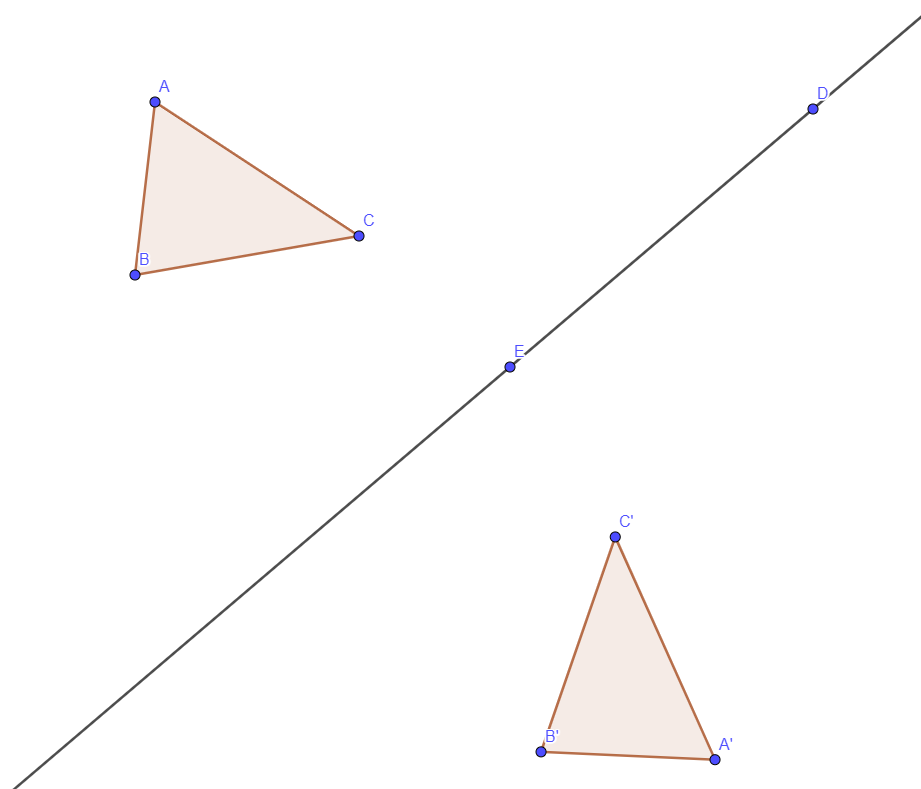
On considère le triangle ABC tel que AB = 4,5 cm, AC = 6 cm et BC = 4 cm. et (d) une droite quelconque :
1- Construire ce triangle.
2-Tracer les symétriques A’ ,B’ et C’ de A ,B et C par rapport à (d).
3- Construire le triangle A’B’C’.
4- Que peut-on dire des segments [AC] et [A’C’] ? Justifier.
5- Quel angle a la même mesure que l’angle BAC ? Justifier.
4-AC=A’C’ car A’,C’ est les symétriques de A et C par rapport à (d)
5- B’A’C’=BAC car A’,B’ et C’ est les symétriques de A,B et C par rapport à (d)
ABC est un triangle rectangle en A tel que : AB= 5 cm et ABC=50°
Soit B’ le symétrique de B par rapport à A.
1- Faire une figure
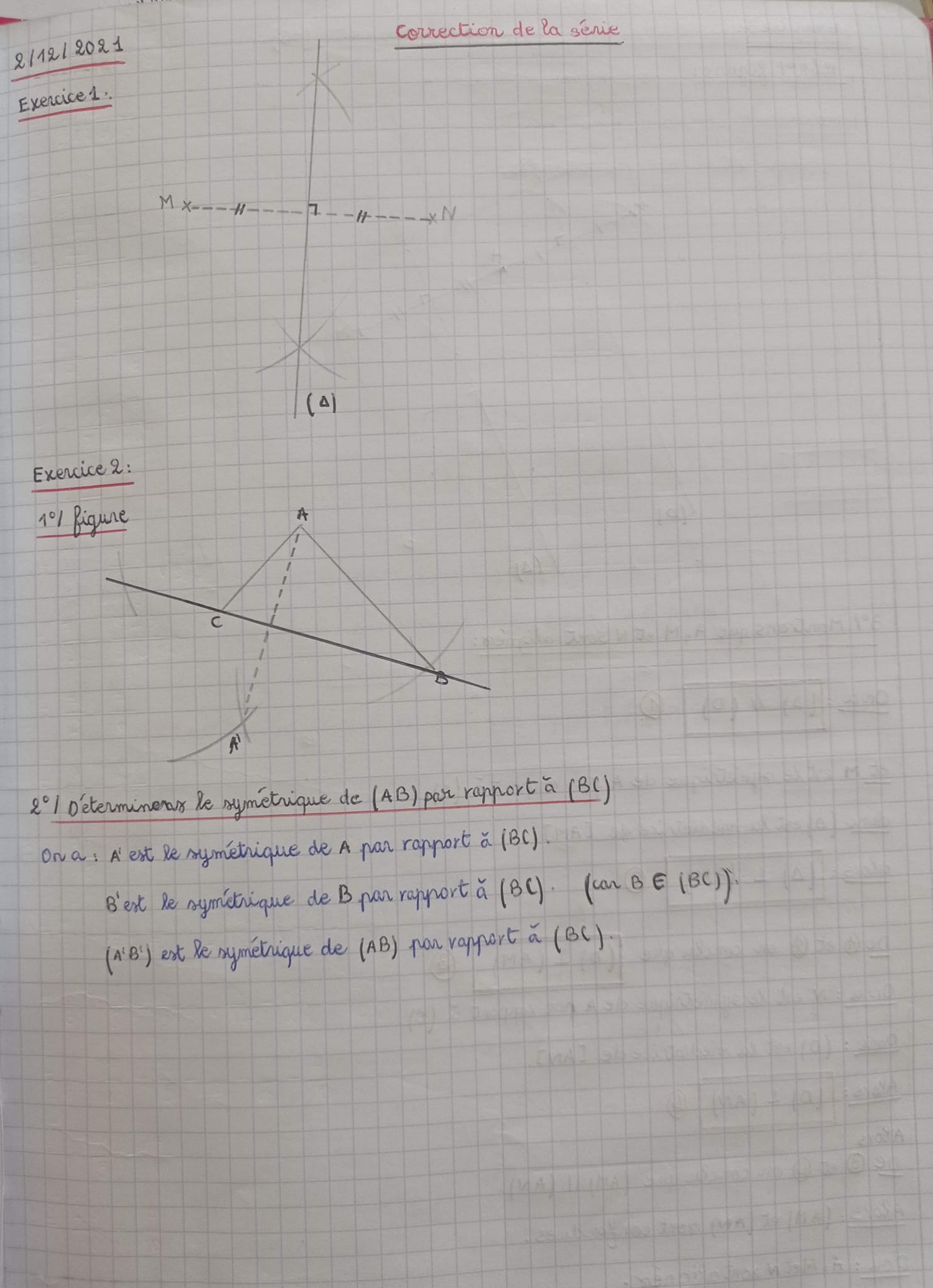
2- Montrer que B’ est le symétrique de B par rapport à (AC).
3- En déduire la mesure de l’angle CB’B
Soit D un point de BC (D≠ B et D ≠ C)
4- Construire D’ le symétrique de D par rapport à la droite (AC)
5-Montrer que : BD=B’D’
6- Montrer que les points D’, B’ et C sont alignés.
1-
2- B’ est le symétrique de B par rapport à A, et A∈ (AC) ,donc B’ est le symétrique de B par rapport à (AC).
3- CB’B = ABC = 50°
car la symétrie conserve la mesure des angles.
4- 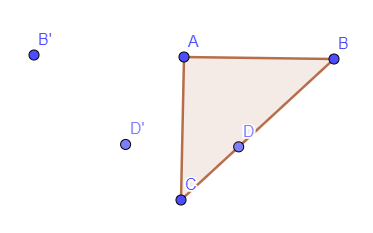
5- B’ est le symétrique de B par rapport à (AC) et D’ est le symétrique de D par rapport à (AC),alors BD=B’D’
6- B’ est le symétrique de B par rapport à (AC)
D’ est le symétrique de D par rapport à (AC)
C est le symétrique de C par rapport à (AC)
tel que les points B,D et C sont alignés alors B’,D’ et C sont aussi alignés.