Symétrie centrale exercices corrigés
📍Exercice 1 :
📐Compléter chaque phrase
Symétrie centrale : Utiliser la figure ci-dessous

1) … est le symétrique de A par rapport à O
2) … est le symétrique de G par rapport à E
3) … est le symétrique de T par rapport à K
4) Q est le symétrique de … par rapport à P
5) O est le symétrique de … par rapport à L
6) B est le symétrique de … par rapport à M
7) C est le symétrique de Q par rapport à …
8) E est le symétrique de A par rapport à …
9) X est le symétrique de H par rapport à …
10) W est le symétrique de A par rapport à …
1) \(S\) est le symétrique de A par rapport à O
2) \(C\) est le symétrique de G par rapport à E
3) \(H\) est le symétrique de T par rapport à K
4) Q est le symétrique de \(A\) par rapport à P
5) O est le symétrique de \(I\) par rapport à L
6) B est le symétrique de \(V\) par rapport à M
7) C est le symétrique de Q par rapport à \(O\)
8) E est le symétrique de A par rapport à \(C\)
9) X est le symétrique de H par rapport à \(I\)
10) W est le symétrique de A par rapport à \(M\)
📍Exercice 2 :
1️⃣Symétriques par rapport au point O
On considère dans tout cet exercice la symétrie qui a pour centre le point \(O\).
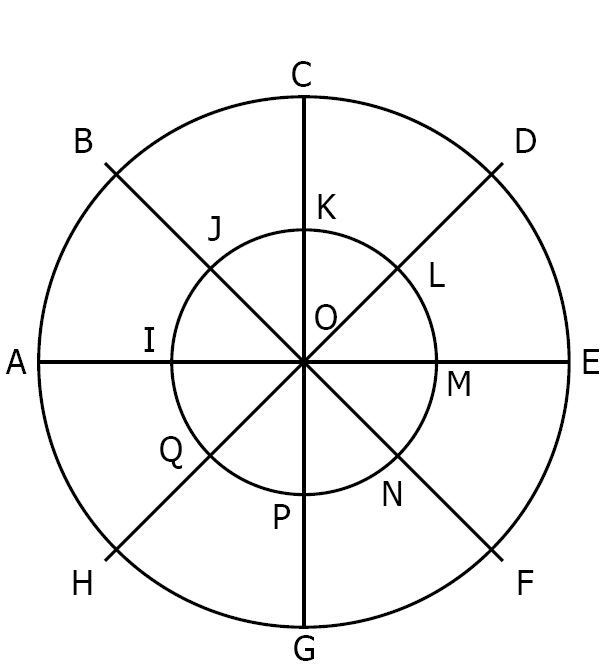
Par cette symétrie, quels sont les symétriques :
de \(A\) ?
de \(B\) ?
de \(M\) ?
de \(D\) ?
de \(E\) ?
de \(P\) ?
de \(G\) ?
de \(L\) ?
de \(O\) ?
2️⃣Compléter les phrases suivantes
Utiliser la définition de la symétrie centrale
a) \(M’\) est le symétrique de \(M\) par rapport à \(O\) signifie que \(O\) est le milieu du segment \([MM’]\).
b) \(B\) est le symétrique de A par rapport à \(O\) signifie que est le milieu du segment \([\)….\(]\).
c) \(F\) est le symétrique de E par rapport à A signifie que est le milieu du segment \([\)….\(]\).
d) \(M’\) est le symétrique de \(M\) par rapport à \(I\) signifie que est le milieu du segment \([\)….\(]\).
e) \(A_2\) est le symétrique de \(A_1\) par rapport à \(M\) signifie que est le milieu du segment \([\)….\(]\).
f) …. est le symétrique de par rapport à signifie que \(A\) est le milieu du segment \([BC]\).
g) …. est le symétrique de par rapport à signifie que \(O\) est le milieu du segment \([MN]\).
h) …. est le symétrique de par rapport à signifie que \(T\) est le milieu du segment \([AA’]\).
📍Exercice 3 :
📏Construction géométrique
Consigne : Construire dans chaque cadre le symétrique du segment par rapport au centre \(O\)
Méthode recommandée :
- Pour chaque segment, déterminer les symétriques de ses extrémités par rapport à \(O\)
- Utiliser la propriété : « Le symétrique d’un segment est un segment de même longueur »
- Tracer le segment entre les deux points symétriques obtenus
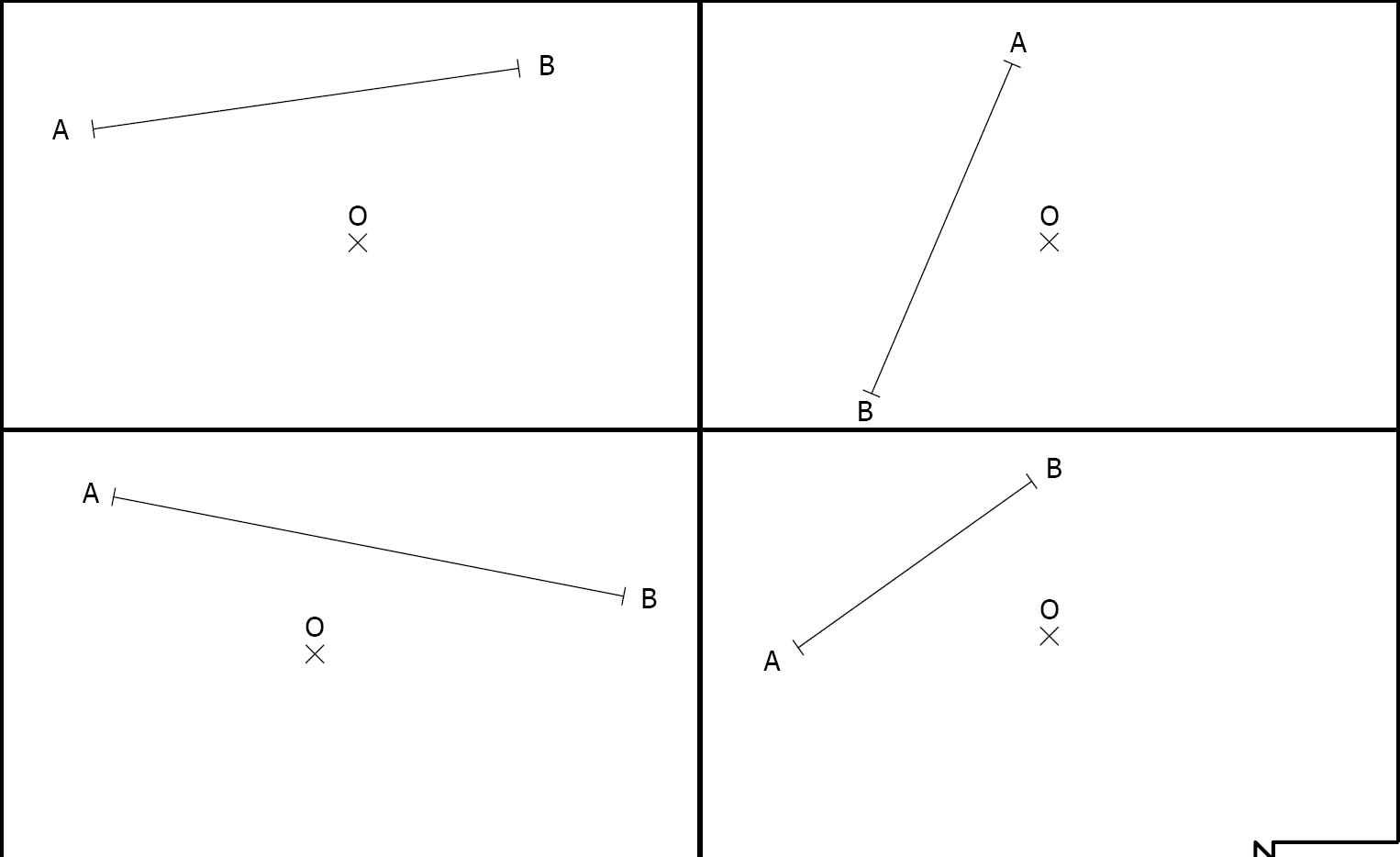
Figure à reproduire et compléter avec les constructions géométriques
💡Astuce
: Pour vérifier votre construction, mesurez la distance entre le centre O et chaque extrémité du segment, puis reportez la même distance de l’autre côté de O.
📍Exercice 4 :
📐Construction géométrique
Consigne : Construire dans chaque cadre le symétrique de la droite \((d)\), puis du point \(M\), par rapport au centre \(O\)
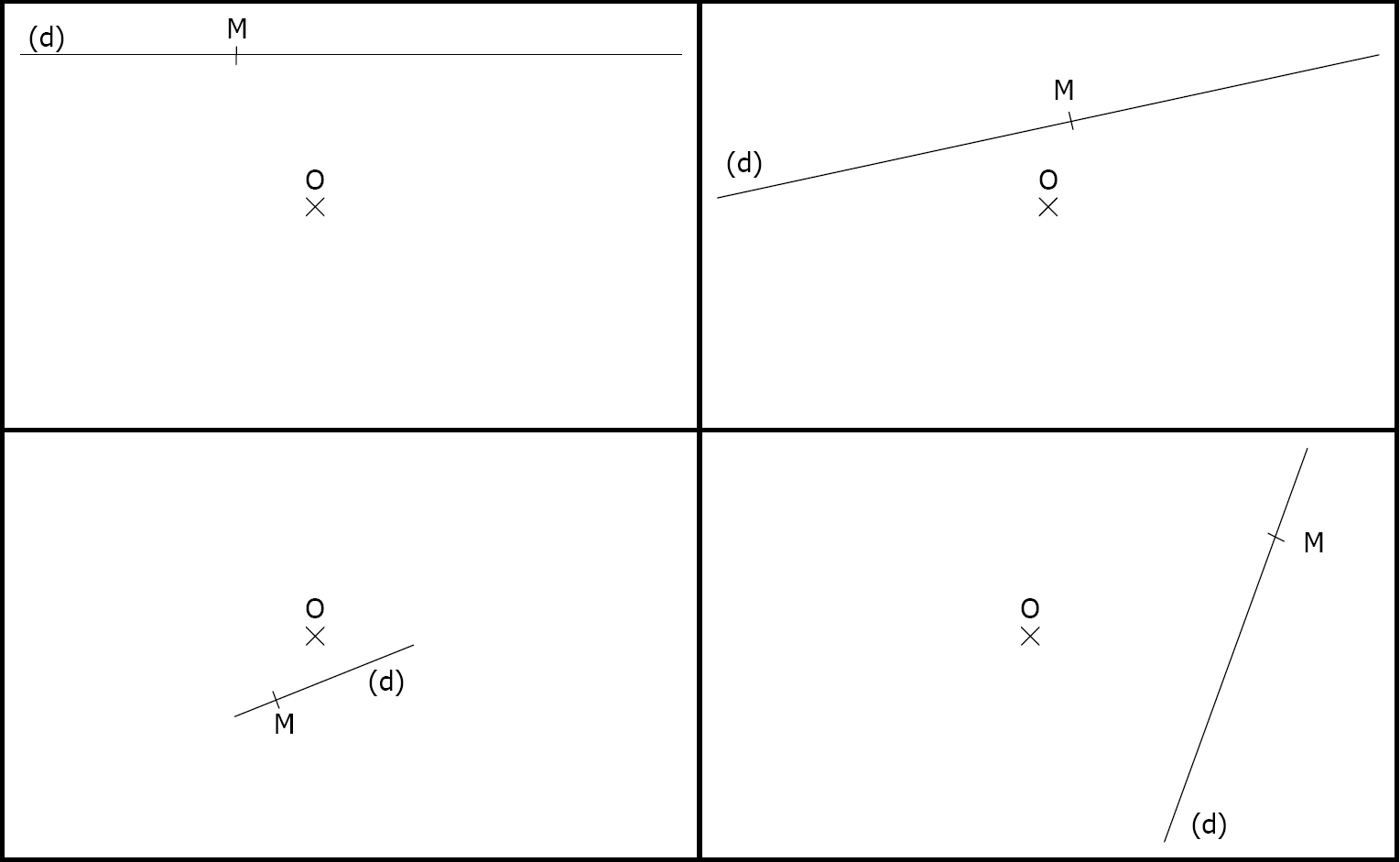
Figure à reproduire et compléter avec les constructions géométriques
📍Exercice 5 :
📐Construction géométrique
Consigne : Construire dans chaque cadre le symétrique de la demi-droite \([Ax)\) par rapport au centre \(O\)

Figure à reproduire et compléter avec les constructions géométriques
📍Exercice 6 :
📐Construction géométrique – Angles
Consigne : Construire le symétrique des angles par rapport au centre \(O\)
🖼️Angles à construire :
Angle 1

Angle 2
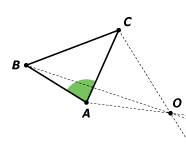
Angle 3
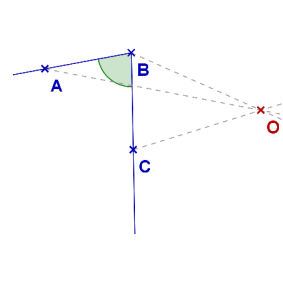
💡Conseils pour la construction :
Pour les sommets :
- Identifier le sommet de chaque angle
- Construire son symétrique par rapport à \(O\)
Pour les côtés :
- Choisir un point sur chaque côté
- Construire leurs symétriques
Vérification :
- Mesurer l’angle initial et son symétrique
- Ils doivent avoir la même mesure
⚠️Attention : Dans une symétrie centrale, l’orientation de l’angle est inversée. Un angle dans le sens horaire devient antihoraire, et vice-versa.
📍Exercice 7 :
📐Construction géométrique – Cercles
Consigne : Construire dans chaque cadre le symétrique du cercle de centre \(I\) par rapport à \(O\)
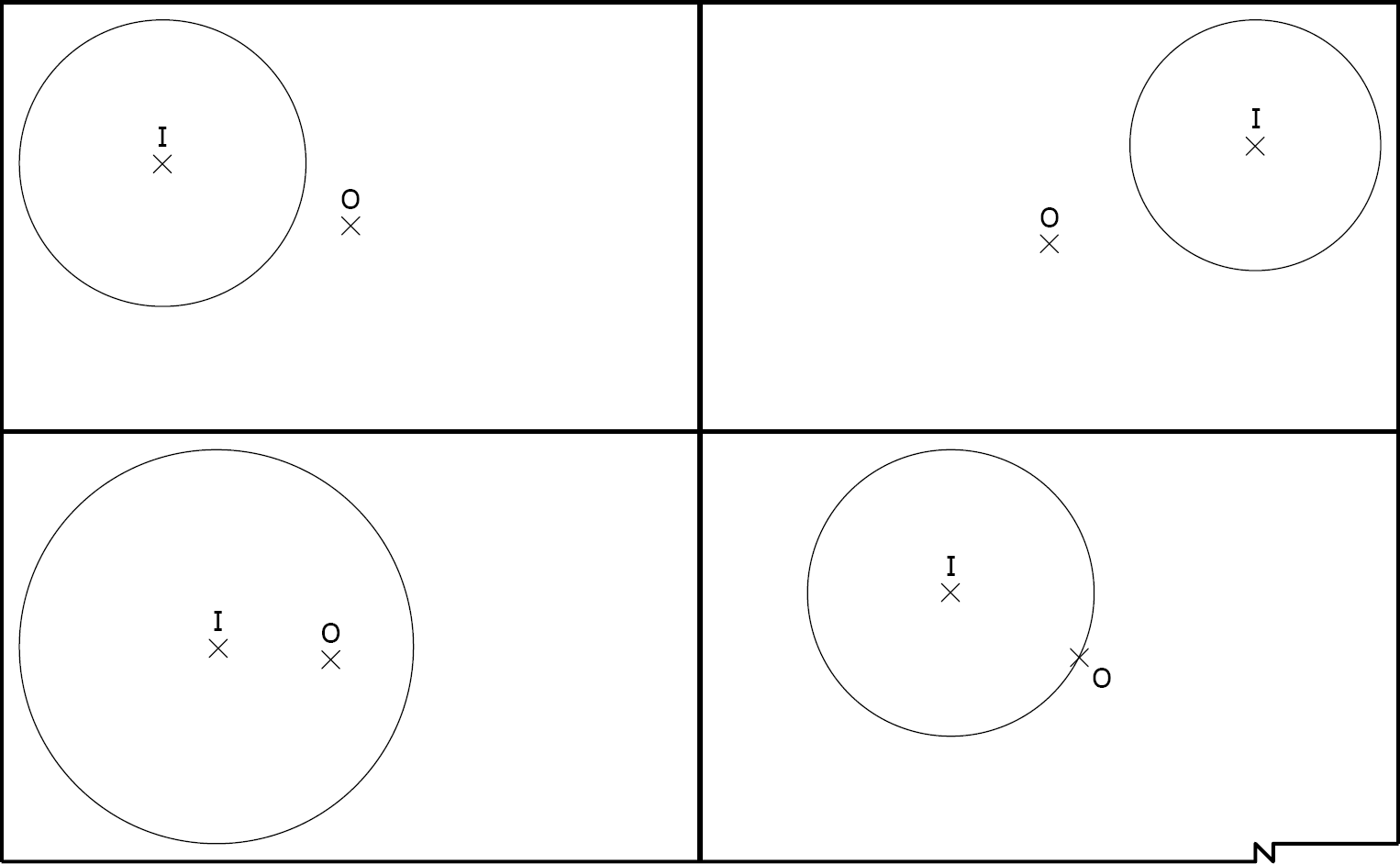
Figure à reproduire et compléter avec les constructions géométriques
💡Vérification : Après construction, mesurer les rayons des cercles initiaux et symétriques. Ils doivent être égaux. Vérifier aussi que \(O\) est bien le milieu de \([II’]\) pour chaque cercle.
📍Exercice 8 :
Consigne : On considère dans tout cet exercice la symétrie de centre \(O\). Identifier les symétriques des différents polygones.
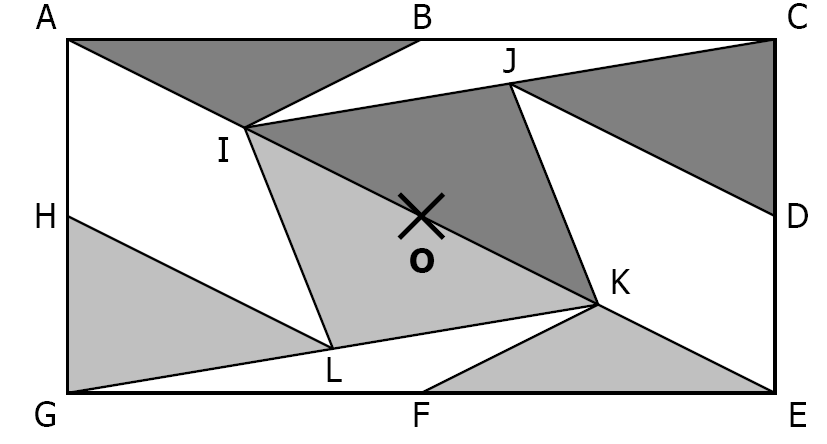
Figure géométrique avec différents triangles, quadrilatères et pentagones
❓Questions :
Triangles :
a) Symétrique du triangle \(ABI\) :
b) Symétrique du triangle \(BCI\) :
c) Symétrique du triangle \(IJK\) :
d) Symétrique du triangle \(GHL\) :
e) Symétrique du triangle \(FGK\) :
f) Symétrique du triangle \(CEI\) :
Quadrilatères et Pentagone :
g) Symétrique du quadrilatère \(DEKJ\) :
h) Symétrique du quadrilatère \(AHLI\) :
i) Symétrique du quadrilatère \(IJKL\) :
j) Symétrique du pentagone \(EFKJD\) :
📍Exercice 9 :
1️⃣Symétrique d’un quadrilatère
Consigne : Construire en rouge le symétrique \(A’B’C’D’\) du quadrilatère \(ABCD\) par rapport à \(O\)
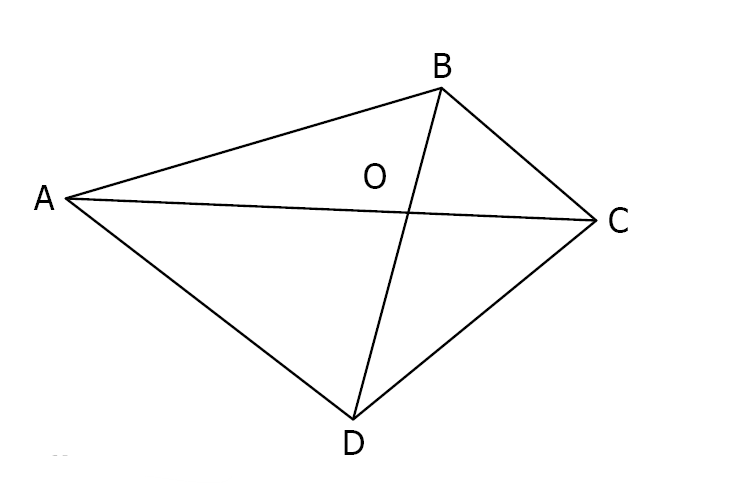
2️⃣Symétrique d’un triangle
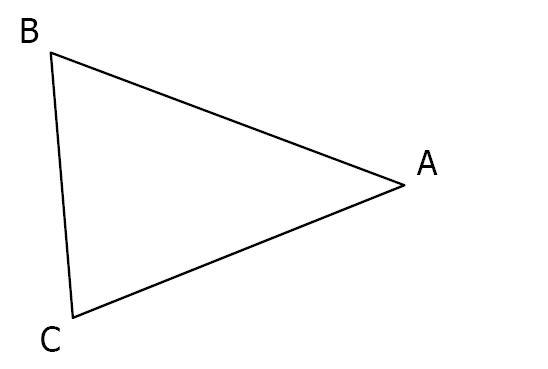
Consigne : Construire le symétrique de ce triangle par rapport au point \(A\)
3️⃣Symétriques de points
Consigne : Construire les symétriques demandés
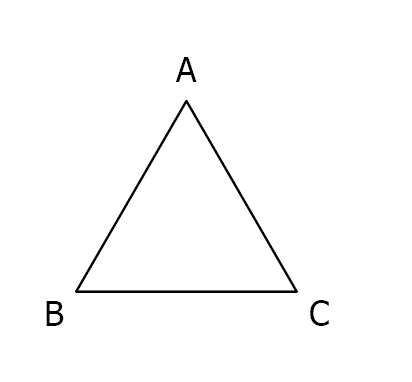
Constructions à réaliser :
a) Construire \(A’\) symétrique de \(A\) par rapport à \(B\)
b) Construire \(B’\) symétrique de \(B\) par rapport à \(C\)
c) Construire \(C’\) symétrique de \(C\) par rapport à \(A\)
📍Exercice 10 :
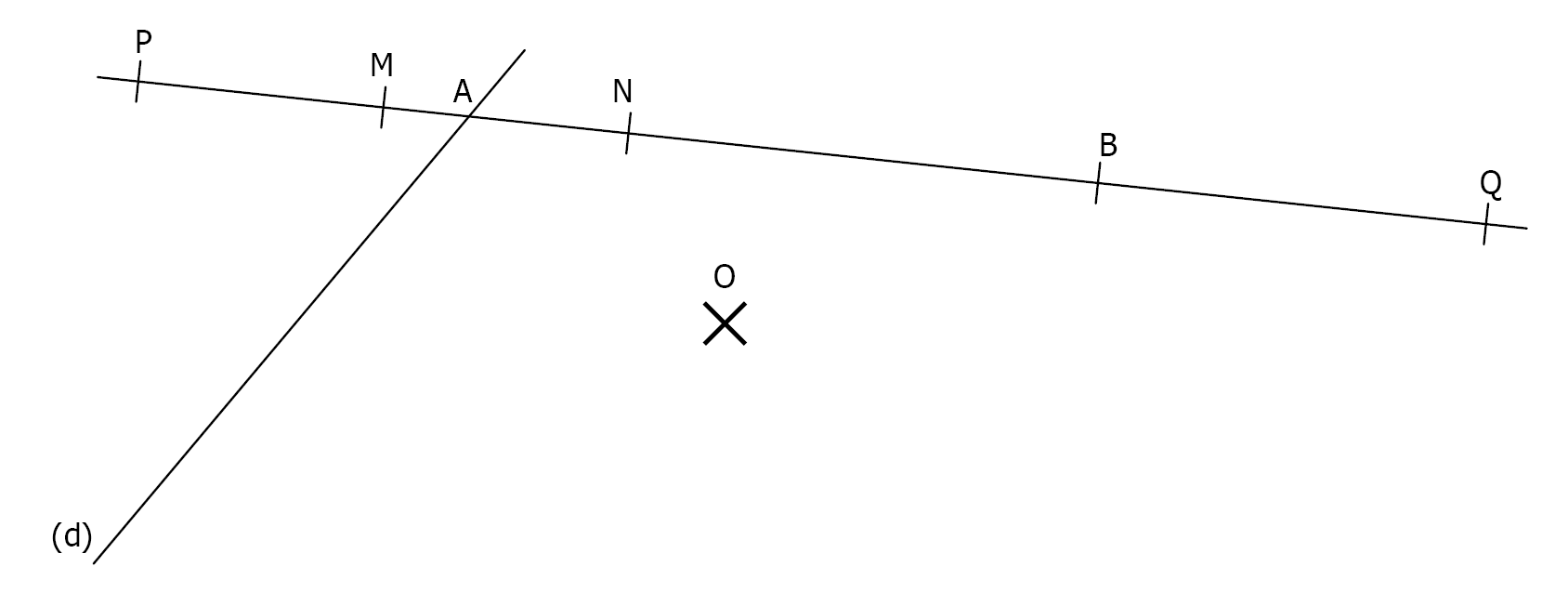
a)Construire les symétriques des droites \((d)\) et \((AB)\) par rapport à \(O\)
b)En utilisant uniquement la règle (sans sa graduation), construire les points \(A’, B’, M’, N’, P’\) et \(Q’\) symétriques des points \(A, B, M, N, P\) et \(Q\)
Méthode sans compas :
- Tracer la droite passant par le point et \(O\)
- Utiliser les propriétés des parallélogrammes pour reporter la distance
- Pour un point \(X\), placer \(X’\) tel que \(O\) soit le milieu de \([XX’]\)
c)Quelle est la nature du quadrilatère \(ABA’B’\) ?
💡Rappel : La construction sans graduation nécessite d’utiliser uniquement les propriétés géométriques (alignement, parallélisme, milieux) et non les mesures.
📍Exercice 11 :
📐On considère le triangle 𝐴𝐵𝐶 tel que :
\(AB = 4,5\ \text{cm}\)
\(AC = 6\ \text{cm}\)
\(BC = 4\ \text{cm}\)
1)Construire le triangle \(ABC\)
2)Tracer les symétriques \(A’\) et \(C’\) de \(A\) et \(C\) par rapport à \(B\)
3)Construire le triangle \(A’BC’\)
4)Que peut-on dire des segments \([AC]\) et \([A’C’]\) ? Justifier.
5) Quel angle a la même mesure que l’angle \(\widehat{BAC}\) ? Justifier.
📍Exercice 12 : Triangle équilatéral et symétrie
📐Triangle équilatéral et symétrie centrale
Objectif : Construire un triangle équilatéral et étudier son symétrique par rapport à un point extérieur
Données :
Triangle équilatéral \(ABC\) avec \(AB = 5\ \text{cm}\)
1)Construction du triangle équilatéral \(ABC\)
2)Construire un point \(O\) extérieur du triangle \(ABC\)
3)Construire les points \(A’\), \(B’\) et \(C’\) symétriques de \(A\), \(B\) et \(C\) par rapport à \(O\)
4) Quelle est la nature du triangle \(A’B’C’\) ? Justifier la réponse par une propriété du cours.
📍Exercice 13 :
Données : Soit \(ABCD\) un carré de côté \(4\ \text{cm}\)
1)Construire le point \(O\) centre de symétrie de \(ABCD\)
2)Construire les points \(E\), \(F\) et \(G\) symétriques respectifs des points \(B\), \(C\) et \(D\) par rapport à \(A\)
3)Symétrique du carré et notations
a) Symétrique du carré :
Quelle est le symétrique de \(ABCD\) par rapport à \(A\) ?
b) Compléter avec la notation \(S_A\) :
\(S_A(A) = \)
\(S_A(CD) = \)
\(S_A([AD)) = \)
4) Quelle est la nature de \(AEFG\) puis calculer son aire.
📐Exercice 14 :
🎯Énoncé du problème
Soit ABC un triangle tel que \( \widehat{ABC} = 50^\circ \) et \( \widehat{BAC} = 70^\circ \), et soit E un point tel que B est le milieu du segment [EC].
1) Construire K, M et D les symétriques de E, B et C respectivement par rapport à A.
2) Déterminer les symétriques des demi-droites [CE] et [BA] par rapport à A.
3) a- Déterminer le symétrique de l’angle \( \widehat{ACB} \) par rapport à A. b- En justifiant votre réponse, déterminer les mesures des angles \( \widehat{AMD} \) et \( \widehat{ADM} \).
📐Exercice 15:
🎯Énoncé du problème
Soit ABC un triangle isocèle en B, tel que AC = 4 cm et \( \widehat{ACB} = 50^\circ \), et soit M un autre point, et soient I, J, K les symétriques respectifs de A, B, C par rapport à M.
1) Déterminer la mesure de \( \widehat{IJK} \).
2) Montrer que IJK est un triangle isocèle.
Rappel : Dans un triangle isocèle, les angles à la base sont égaux.
De plus, la symétrie centrale conserve les longueurs et les mesures d’angles.
📐Exercice 16:
🎯Énoncé du problème
Considérons la figure ci-contre qui représente un quart d’un cercle.
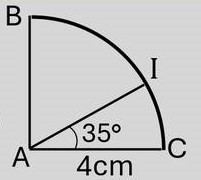
1) Reproduire la figure, puis construire le symétrique de cette figure par rapport au point I.
(Nommer M, N, P les symétriques respectifs de A, B et C par rapport à I)
2) Démontrer que \( (AB) \parallel (MN) \).
3) Déterminer la mesure de l’angle \( \widehat{IMN} \).
📐Exercice 17:
🎯Énoncé du problème
Soit EFG un triangle, et soit M le milieu de [FG], et soit O le milieu de [EM].
1) Construire A et B les symétriques respectifs de F et G par rapport à O.
2) Montrer que E est le milieu de [AB].
Rappel :
• Si O est le milieu d’un segment [XY], alors O est le centre de symétrie du segment.
• La symétrie centrale conserve les milieux.
Symétrie centrale exercices corrigés
