Systèmes de deux équations à deux inconnues exercices corrigés
Exercice 1:
Parmi ces systèmes d’équations, retrouver ceux qui ont pour solution le couple $(2 ; 1)$:
$1)$ $\left\{\begin{array}{l}x+2y=4 \\x-y=3\end{array}\right.$
$2)$ $\left\{\begin{array}{l}x-2y=0 \\3x-y=4\end{array}\right.$
$3)$ $\left\{\begin{array}{l}x+y=3 \\4x-3y=5\end{array}\right.$
$4)$ $\left\{\begin{array}{l}x-y=4 \\3x+y=7\end{array}\right.$
$1)$ $\left\{\begin{array}{l}x+2 y=4 \\ x-y=3\end{array}\right.$
$x+2 y =\underline{2}+2 \times \underline{1} =2+2 =4 \rightarrow \text { OUI }$
$x-y =\underline{2}-1 =1 \neq 3 \rightarrow \mathrm{NON}$
$(2;1)$ n’est pas une solution du système.
$2)$ $\left\{\begin{array}{l}x-2 y=0 \\ 3 x-y=4\end{array}\right.$
$x-2 y =2-2 \times 1 =0 \rightarrow \mathrm{OUI}$
$3 x-y =3 \times 2-1 =5 \rightarrow \mathrm{NON}$
$( 2 ; 1 )$ n’est pas une solution du système.
$3)$ $\left\{\begin{array}{l}x+y=3 \\ 4 x-3 y=5\end{array}\right.$
$x+y =2+1 =3 \rightarrow \mathrm{OUI}$
$4x-3y =4×2-3×1 =5 \rightarrow \mathrm{OUI}$
$(2 ; 1)$ est une solution du système.
$4)$ $\left\{\begin{array}{l}x-y=4 \\ 3 x+y=7\end{array}\right.$
$x-y =2-1 =1 \neq 4 \rightarrow \mathrm{NON}$
$( 2 ; 1 )$ n’est pas une solution du système.
Exercice 2:
$1)$ Exprimer $x$ en fonction de $y$ : 1. Exprimer x en fonction de y :
$a)$ $x+y=1 $
$ b)$ $3 y+2 x=5 $
$ c)$ $x+6 y=-2 $
$2)$ Exprimer $y$ en fonction de $x$ :
$ d)$ $x+3 y=4 $
$e)$$-x+2 y=1 $
$ f)$ $ 2 x+y=3 $
$1)$
$a)$ $x+y=1 $
$x=1-y$
$ b)$ $3 y+2 x=5 $
$2 x=5-3 y $
$x=\frac{5-3 y}{2}$
$ c)$ $x+6 y=-2 $
$x=-2-6 y$
$2)$
$ d)$ $x+3 y=4 $
$-3 y=4-x$
$y=-\frac{4-x}{3}$
$e)$ $-x+2 y=1 $
$2y=1+x$
$y=\frac{1+x}{2}$
$ f)$ $ 2 x+y=3 $
$y=3-2x$
Exercice 3:
Résoudre ce système par substitution : $\quad\left\{\begin{array}{l}x+y=3 \\ x-y=1 \end{array}\right.$
$\quad\left\{\begin{array}{l}\underline{x}+y=3 \quad (1) \\ x-y=1 \quad (2)\end{array}\right.$
On remplace x par ${ }^{(*)}$ dans (2) :
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\3-y-y=1 \quad (2)\end{array}\right.$
On réduit le membre de gauche de $(2)$
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\3-2 y=1 \quad (2)\end{array}\right.$
On isole $y$ dans $(2)$ :
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\-2 y=1-3 \quad (2)\end{array}\right.$
On calcule le membre de droite de $(2)$
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\-2 y=-2 \quad (2)\end{array}\right.$
On divise les 2 membres de $(2)$ par le coefficient de $y$ :
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\\frac{-2 y}{-2}=\frac{-2}{-2} \quad (2)\end{array}\right.$
On calcule et on obtient y :
$\quad\left\{\begin{array}{l}x=3-y \quad (1) \\y=1 \quad (2)\end{array}\right.$
On remplace $y$ par sa valeur dans la première équation
$\quad\left\{\begin{array}{l}x=3-1=2 \quad (1) \\y=1 \quad (2)\end{array}\right.$
Donc : $\quad\left\{\begin{array}{l}x=2 \\y=1 \end{array}\right.$
Exercice 4:
Résoudre ces systèmes par substitution :
$1)$ $\left\{\begin{array}{l}x+y=5 \\ x-y=1\end{array} \right.$
$2)$ $\left\{\begin{array}{l}x+y=15 \\ 2 x+y=21\end{array}\right.$
$3)$ $\left\{\begin{array}{l}3 x+4 y=24 \\ x+5 y=19\end{array}\right.$
$1)$
$\left\{\begin{array}{l}x+y=5 \\ x-y=1\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\ 5-y-y=1\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\5-2 y=1\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\ -2 y=1-5\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\ -2 y=-4\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\\frac{-2 y}{-2}=\frac{-4}{-2}\end{array} \right.$
$\left\{\begin{array}{l}x=5-y \\y=2\end{array} \right.$
$\left\{\begin{array}{l}x=5-2 \\ y=2\end{array} \right.$
$\left\{\begin{array}{l}x=3 \\ y=2\end{array} \right.$
$2)$
$\left\{\begin{array}{l}x+y=15 \\ 2 x+y=21\end{array}\right.$
$\left\{\begin{array}{l}x=15-y \\ 2(15-y)+y=21\end{array} \right.$
$\left\{\begin{array}{l}x=15-y\\30-2 y+y=21\end{array} \right.$
$\left\{\begin{array}{l}x=15-y \\ – y=21-30\end{array} \right.$
$\left\{\begin{array}{l}x=15-y \\ – y=-9\end{array} \right.$
$\left\{\begin{array}{l}x=15-y \\y=9\end{array} \right.$
$\left\{\begin{array}{l}x=15-9 \\y=9\end{array} \right.$
$\left\{\begin{array}{l}x=6 \\ y=9\end{array} \right.$
$3)$
$\left\{\begin{array}{l}3 x+4 y=24 \\ x+5 y=19\end{array}\right.$
$\left\{\begin{array}{l}3 x+4 y=24\\ x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}3(19-5 y)+4 y=24\\ x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}57-15 y+4 y=24\\ x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}-11y=24-57 \\ x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}-11y=-33 \\x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}y=3 \\x=19-5 y\end{array} \right.$
$\left\{\begin{array}{l}y=3 \\ x=19-5×3\end{array} \right.$
$\left\{\begin{array}{l}y=3 \\ x=4\end{array} \right.$
Exercice 5:
Multiplier chaque équation par le nombre indiqué, puis additionner ou soustraire pour éliminer l’une des deux inconnues, et enfin trouver $x$ 0u $y$ :
$1)$ $\left \{\begin{array}{l}2 \times (2x+3y=5) \\3 \times (5x-2y=3)\end{array} \right.$
$2)$ $\left \{\begin{array}{l}5 \times (2x+3y=4) \\-2 \times (5x-y=7)\end{array} \right.$
$1)$ $\left \{\begin{array}{l}2 \times (2x+3y=5) \\3 \times (5x-2y=3)\end{array} \right.$
$\left \{\begin{array}{l}4x+6y=10 \\15x-6y=9\end{array} \right.$
$(4x+6y)+(15x-6y)=10+9$
$4x+15x+6y-6y=19$
$19x=19$
$x=1$
$2)$ $\left \{\begin{array}{l}5 \times (2x+3y=4) \\-2 \times (5x-y=7)\end{array} \right.$
$\left \{\begin{array}{l}10x+15y=20 \\-10x+2y=-14\end{array} \right.$
$10x+15y-10x+2y=20-14$
$17y=6$
$y=\frac{6}{17}$
Exercice 6:
Résoudre ces systèmes par combinaison :
$1)$ $\left\{\begin{array}{l}3x+4y=9 \\ 5x+6y=14\end{array} \right.$
$2)$ $\left\{\begin{array}{l}2x+3y=-11 \\ 3x-5y=12\end{array} \right.$
$3)$ $\left\{\begin{array}{l}6x-5y=2 \\ -7x+3y=1\end{array} \right.$
$\rightarrow$ repérez les plus petits coefficients !
$1)$ $\left\{\begin{array}{l} 5 \times (3x+4y=9) \\ -3 \times(5x+6y=14)\end{array} \right.$
$\left\{\begin{array}{l} 15x+20y=45 \\ -15x-18y=-42\end{array} \right.$
$(15x+20y)+ (-15x-18y)= 45-42$
$15x+20y-15x-18y= 3$
$2y= 3$
$y= \frac{3}{2}$
On utilise alors la ligne de son choix dans le système, de préférence celle ayant les plus petits coefficients.
On a : $3x+4y=9$
$3x+4\times\frac{3}{2}=9$
$3x+6=9$
$3x=9-6$
$3x=3$
$x=1$
La solution du système est donc le couple $(1 ; \frac{3}{2})$
$2)$ $\left\{\begin{array}{l}3 \times(2x+3y=-11) \\ -2 \times(3x-5y=12)\end{array} \right.$
$\left\{\begin{array}{l}6x+9y=-33 \\ -6x+10y=-24\end{array} \right.$
$6x-6x+9y+10y=-33-24$
$19y=-57$
$y= \frac{-57}{19}$
$y=-3$
Calculons $x$ :
On a : $2x+3y=-11$
$2x+3(-3)=-11$
$2x-9=-11$
$2x=-11+9$
$2x=-2$
$x=-1$
La solution du système est donc le couple $(-1 ; -3)$
$3)$ $\left\{\begin{array}{l}3 \times(6x-5y=2) \\ 5 \times(-7x+3y=1)\end{array} \right.$
$\left\{\begin{array}{l}18x-15y=6 \\ -35x+15y=5\end{array} \right.$
$18x-35x-15y+15y=6+5$
$-17x=11$
$x=-\frac{11}{17}$
Calculons $y$ :
On a : $-7x+3y=1$
$-7×(-\frac{11}{17})+3y=1$
$\frac{77}{17}+3y=1$
$3y=1-\frac{77}{17}$
$3y=-\frac{60}{17}$
$y=-\frac{60}{3×17}=-\frac{20}{17}$
La solution du système est donc le couple $(-\frac{11}{17} ; -\frac{20}{17})$
Exercice 7:
$1)$ Résoudre graphiquement le système suivant :
$\quad\left\{\begin{array}{l}5x+4y=16 \quad (1) \\3x+6y=15 \quad (2)\end{array}\right.$
$2)$ Résoudre graphiquement le système suivant pour $0 ≤ x ≤ 20$
$\quad\left\{\begin{array}{l}x+y=29 \quad (1) \\x-y=5 \quad (2)\end{array}\right.$
$3)$ Résoudre graphiquement le système suivant pour $-5 ≤ x ≤ 5$
$\quad\left\{\begin{array}{l}2x-y=1 \quad (1) \\3x+5y=21 \quad (2)\end{array}\right.$
$4)$ Résoudre graphiquement le système suivant pour $-5 ≤ x ≤ 5$
$\quad\left\{\begin{array}{l}4x-y=18 \quad (1) \\x+9y=-14 \quad (2)\end{array}\right.$
$1)$ Résoudre graphiquement le système suivant :
$\quad\left\{\begin{array}{l}5x+4y=16 \quad (1) \\3x+6y=15 \quad (2)\end{array}\right.$
1er étape :
Tracer les deux droites ayant équations les deux équations $(1)$ et $(2)$ du système.
• Tracé de la droite ${D}_{1}$ correspondant à l’équation $ (1) : 5x+4y=16$ :
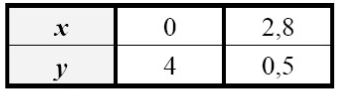
• Tracé de la droite ${D}_{2}$ correspondant à l’équation $ (2) : 3x+6y=15$ :

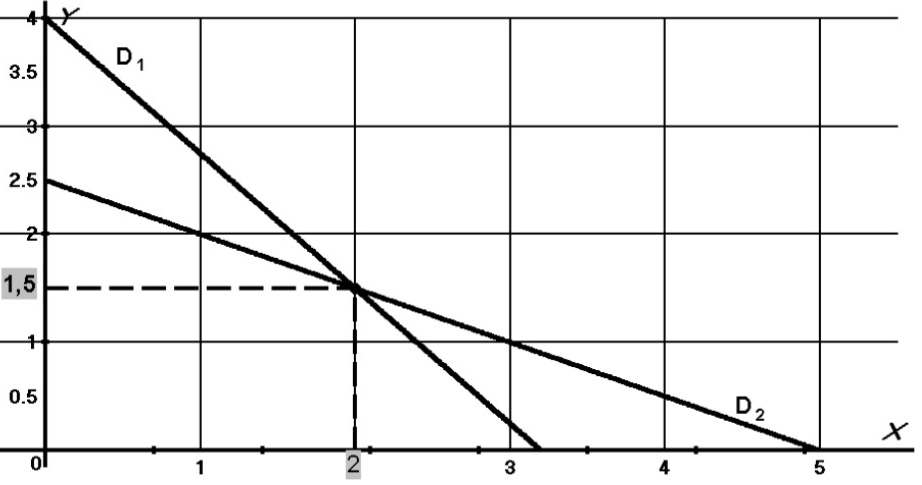
• Lire et écrire les coordonnées du points d’intersection.
2ème étape :
• Donner la solution du système.
Le couple $(x;y)$ solution du système est égal à $(2;1,5)$
$2)$ Résoudre graphiquement le système suivant pour $0 ≤ x ≤ 20$
$\quad\left\{\begin{array}{l}x+y=29 \quad (1) \\x-y=5 \quad (2)\end{array}\right.$
• Tracé de la droite ${D}_{1}$ correspondant à l’équation $ (1) : x+y=29$ :

• Tracé de la droite ${D}_{2}$ correspondant à l’équation $ (2) : x-y=5$ :
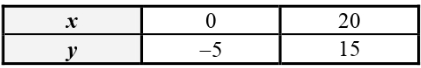
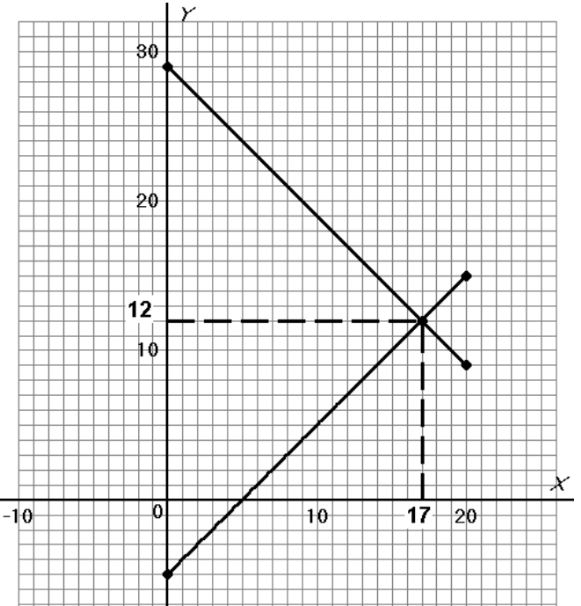
Le couple $(x;y)$ solution du système est égal à $(17;12)$
$3)$ Résoudre graphiquement le système suivant pour $-5 ≤ x ≤ 5$
$\quad\left\{\begin{array}{l}2x-y=1 \quad (1) \\3x+5y=21 \quad (2)\end{array}\right.$
• Tracé de la droite ${D}_{1}$ correspondant à l’équation $ (1) : 2x-y=1$ :
• Tracé de la droite ${D}_{2}$ correspondant à l’équation $ (2) : 3x+5y=21$ :

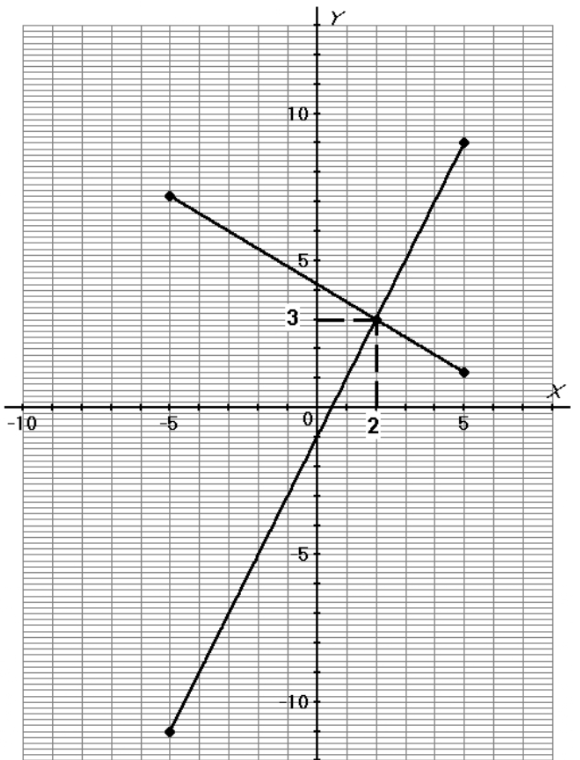
Le couple $(x;y)$ solution du système est égal à $(2;3)$
$4)$ Résoudre graphiquement le système suivant pour $-5 ≤ x ≤ 5$
$\quad\left\{\begin{array}{l}4x-y=18 \quad (1) \\x+9y=-14 \quad (2)\end{array}\right.$
• Tracé de la droite ${D}_{1}$ correspondant à l’équation $ (1) : 4x-y=18 $ :

• Tracé de la droite ${D}_{2}$ correspondant à l’équation $ (2) : x+9y=-14 $ :
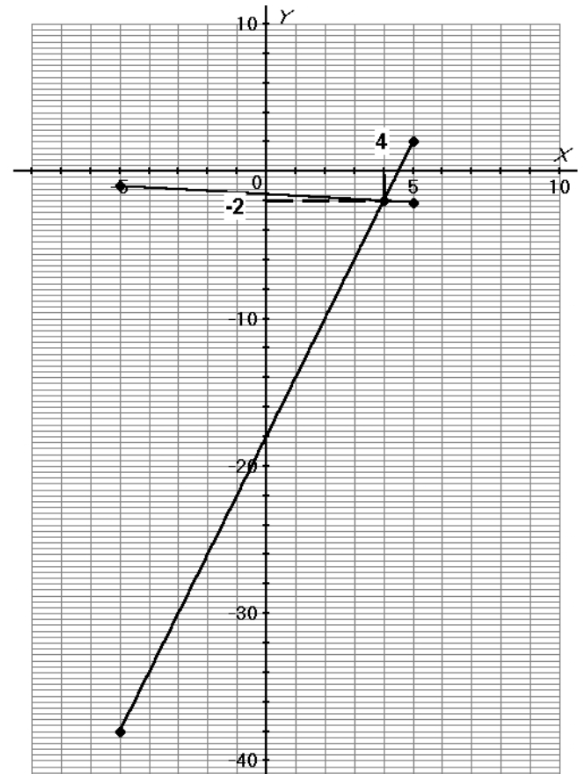
Le couple $(x;y)$ solution du système est égal à $(4;-2)$
Exercice 8:
$1)$ Résoudre le système d’équations: $\left\{\begin{array}{l}3 x+1 y=15,5 \\2 x+3 y=20,60 \end{array}\right.$
$2)$ Un client achète $3$ baguettes et $1$ pain, il paie $15,50 \mathrm{DH}$.
Un autre client achète $2$ baguettes et $3$ pains et paie $20,60 \mathrm{DH}$.
• Expliquer pourquoi la solution est celle du système résolu en $1)$,et quel est le prix d’une baguette et quel est le prix d’un pain ?
$1)$ Résolution du système : (Par substitution)
$ \left\{\begin{array} { l }{ 3 x + 1 y = 1 5 , 5 } \\{ 2 x + 3 y = 2 0 , 6 0 }
\end{array}\right.$
$ \left\{\begin{array} { l }{ y = 1 5 , 5 – 3 x } \\ { 2 x + 3 ( 1 5 , 5 – 3 x ) = 2 0 , 6 } \end{array} \right.$
$\left\{\begin{array}{l}y=15,5-3 x \\2 x+46,5-9 x=20,6 \end{array}\right.$
$\left\{\begin{array} { l }{ y = 1 5 , 5 – 3 x } \\
{ 2 5 , 9 = 7 x }\end{array} \right.$
$\left\{\begin{array}{l}y=15,5-3 \times 3,7=4,4 \\x=3,7
\end{array}\right.$
Le couple $(x;y)$ solution du système est égal à $(3,7;4,4)$
$2)$ Un client achète $3$ baguettes et $1$ pain, il paie $15,50 \mathrm{DH}$.
Un autre client achète $2$ baguettes et $3$ pains et paie $20,60 \mathrm{DH}$.
• Expliquer pourquoi la solution est celle du système résolu en $1)$,et quel est le prix d’une baguette et quel est le prix d’un pain ?
En nommant $x$ le prix d’une baguette de pain et $y$ le prix d’un pain, on obtient le même système d’équations qu’en $1)$.
Donc le prix d’une baguette est $3,70 \mathrm{DH}$ et le prix d’un pain est $4,40 \mathrm{DH}$. (Faire la vérification)
Exercice 9:
$1)$ Résoudre le système d’équations : $ \left\{\begin{array} { l }{ x + y = 31 } \\{ 2 x + 5 y = 113}\end{array}\right.$
$2)$ On dispose d’une somme de $11300 \mathrm{DH}$ constituée de $31$ billets, les uns de $200 \mathrm{DH}$, les autres de $500 \mathrm{DH}$.
On cherche le nombre de billets de $200 \mathrm{DH}$ et le nombre de billets de $500 \mathrm{DH}$.
• Ecrire le système de deux équations à deux inconnues correspondant au problème, et expliquer pourquoi ce système se ramène au système résolu en $1)$.
• Indiquer alors le nombre de billets de $200 \mathrm{DH}$ et de $500 \mathrm{DH}$.
$1)$ $ \left\{\begin{array} { l }{ x + 1y = 31 } \\{ 2 x + 5 y = 113}\end{array}\right.$
$\left\{\begin{array}{l}x=31-y \\ 2(31-y)+5 y=113\end{array}\right.$
$\left\{\begin{array} { l }{ x = 3 1 – y } \\{ 6 2 – 2 y + 5 y = 1 1 3 }
\end{array}\right.$
$\left\{\begin{array} { l }{ x = 3 1 – y } \\{ 3 y = 1 1 3 – 6 2 }
\end{array}\right.$
$\left\{\begin{array}{l}x=14 \\y=\frac{51}{3}=17
\end{array}\right.$
Le couple $(x;y)$ solution du système est égal à $(14;\frac{51}{3})$
$2)$
En nommant $x$ le nombre de billets de $200 \mathrm{DH}$ et $y$ le nombre de billets de $500 \mathrm{DH}$, l’énoncé permet d’écrire deux équations:
$\left\{\begin{array}{l}x+y=31 \\20 x+50 y=1130\end{array}\right.$
En divisant par $10$ les membres de la deuxième équation du système on obtient le système résolu en $1)$ , qui a donc la même solution.
La somme de $11300 \mathrm{DH}$ est donc constituée de $x=14$ billets de $200 \mathrm{DH}$ et de $y=17$ billets de $500 \mathrm{DH}$.
Exercice 10:
$1)$ Résoudre le système : $ \left\{\begin{array} { l }{ 2 x+3 y=18 } \\{ x+4 y=19}\end{array}\right.$
$2)$ Dans un concours hippique un cavalier est pénalisé:
• Quand le cheval refuse de sauter un obstacle,
• Quand le cheval fait tomber la barre.
Le cheval de Pierre a fait $2$ refus et a fait tomber $3$ barres pour un total de $18$ points de pénalité.
Le cheval de Jean a fait $1$ refus et a fait tomber $4$ barres pour un total de $19$ points.
– Combien de points coûte un refus? ….
– Combien de points coûte la chute d’une barre? …..
$1)$ $ \left\{\begin{array} { l }{ 2 x+3 y=18 } \\{ x+4 y=19}\end{array}\right.$
$ \left\{\begin{array} { l }{ -1(2 x+3 y=18) } \\{ 2(x+4 y=19)}\end{array}\right.$
$ \left\{\begin{array} { l }{ -2 x-3 y=-18 } \\{ 2x+8 y=38}\end{array}\right.$
$-2 x-3 y+2x+8 y=38-18$
$5 y=20$
$y=\frac{20}{5}=4$
Calculons $x$:
On a : $x+4 y=19$
$x+4×4=19$
$x+16=19$
$x=19-16=3$
Le couple $(x;y)$ solution du système est égal à $(3;4)$
$2)$ En nommant $x$ le coût d’un refus et $y$ le coût de la chute d’une barre, le problème a pour solution le système d’équations en $2)$, donc un refus coûte $3$ points et une chute de barre coûte $4$ points.
Exercice 11:
Mourad a acheté $3$ DVD et $4$ CD pour $990 \mathrm{DH}$.
Sa sœur Fatiha a payé $680 \mathrm{DH}$ pour $2$ DVD et $3$ CD.
On désignera par $x$ le prix de chaque DVD et par $y$ le prix de chaque CD.
• Mettre le problème en équation puis calculer le prix d’un DVD et celui d’un CD.
Le système d’équation est : $ \left\{\begin{array} { l }{ 3 x+4 y=990 } \\{ 2 x+3 y=680}\end{array}\right.$
$ \left\{\begin{array} { l }{ -2(3 x+4 y=990) } \\{ 3(2 x+3 y=680)}\end{array}\right.$
$ \left\{\begin{array} { l }{ -6 x-8 y=-1980) } \\{ 6 x+9 y=2040)}\end{array}\right.$
Par combinaison, on supprime la variable $x$:
$-6 x-8 y+ 6 x+9 y=-1980+2040$
$y=60$
Calculons la variable $x$ :
On a : $ 2 x+3 y=680$
$ 2 x+3×60=680$
$ 2 x+180=680$
$ 2 x=680-180$
$ 2 x=500$
$ x=250$
Le prix x d’un DVD est $250 \mathrm{DH}$ et le prix y d’un CD est $60 \mathrm{DH}$.
Exercice 12:
Amine a acheté cinq tee-shirts et deux jeans : il a payé $680 \mathrm{DH}$ .
Tarik a acheté quatre tee-shirts, un jean et un blouson qui coûte $600 \mathrm{DH}$ : il a payé $1060 \mathrm{DH}$.
• Quel est le prix d’un tee-shirt ? Quel est le prix d’un jean ?
En notant $x$ le prix d’un tee-shirt et $y$ celui d’un jean, on obtient :
$\left\{\begin{array} { l }{ 5 x + 2 y = 6 8 0 } \\{ 4 x + y + 6 0 0 = 1 0 6 0 }
\end{array}\right. $
Donc $ \left\{\begin{array} { l }{ 5 x + 2 y = 6 8 0 } \\{ 4 x + y = 1 0 6 0 – 6 0 0 }
\end{array} \right.$
Donc $ \left\{\begin{array}{l}5 x+2 y=680 \\4 x+y=460 \end{array}\right.$
Par substitution, en isolant $y$ dans la deuxième équation, on obtient :
On a: $\left\{\begin{array}{l}5 x+2 y=680 \\ y=460-4 x\end{array}\right.$
Donc, $\left\{\begin{array}{l}5 x+2(460-4 x)=680 \\ y=460-4 x\end{array}\right.$
Donc : $\left\{\begin{array}{l}5 x+920-8 x=680 \\ y=460-4 x\end{array}\right.$
Donc, $\left\{\begin{array}{c}-3 x=680-920 \\ y=460-4 x\end{array}\right.$
Donc : $\left\{\begin{array}{c}-3 x=-240 \\y=460-4 x\end{array}\right.$
Donc : $\left\{\begin{array}{l}x=-240:(-3) \\y=460-4 x\end{array}\right.$
Donc, $\left\{\begin{array}{l}x=80 \\ y=460-4 x\end{array}\right.$
Donc, $\left\{\begin{array}{l}x=80 \\ y=460-4 \times 80\end{array}\right.$
Donc, $\left\{\begin{array}{l}x=80 \\ y=140\end{array}\right.$
Le système admet une seule solution : le couple $( 80 ; 140)$.
Le prix d’un tee-shirt est $80 \mathrm{DH}$ et y celui d’un jean $140 \mathrm{DH}$
Exercice 13:
Un premier bouquet de fleur est composé de $3$ iris et $4$ roses jaunes, il coûte $48 \mathrm{DH}$.
Un second bouquet est composé de $5$ iris et de $6$ roses jaunes, il coûte $75 \mathrm{DH}$.
On appelle $x$ le prix en $ \mathrm{DH}$ d’un iris et $y$ le prix en $ \mathrm{DH}$ d’une rose jaune.
• Ecrire un système d’équations traduisant les données de ce problème et calculer le prix d’un iris et celui d’une rose jaune.
$x$ est le prix en $ \mathrm{DH}$ d’un iris et $y$ le prix en $ \mathrm{DH}$ d’une rose jaune.
Mise en équations du problème :
$\left\{\begin{array}{l}3 x+4 y=48 \\ 5 x+6 y=75\end{array} \rightarrow \quad\left\{\begin{array}{ll}3 x+4 y=48 & \times(-3) \\ 5 x+6 y=75 & \times 2\end{array}\rightarrow\left\{\begin{array}{l}-9 x-12 y=-144 \\ 10 x+12 y=150\end{array}\right.\right.\right.$
Additionnons les deux égalités membre à membre on obtient :
$-9 x-12 y+ 10 x+12 y=-144+150$
$x=6$.
Comme : $3 x+4 y=48 \quad$
On a : $3 \times 6+4 y=48 $
$ 4 y=48-18=30 $
$ y=7,5$
Donc le prix d’un iris est de $6 \mathrm{DH}$ et celui d’une rose jaune de $7 , 5 \mathrm{DH}$.
Systèmes de deux équations à deux inconnues exercices corrigés
