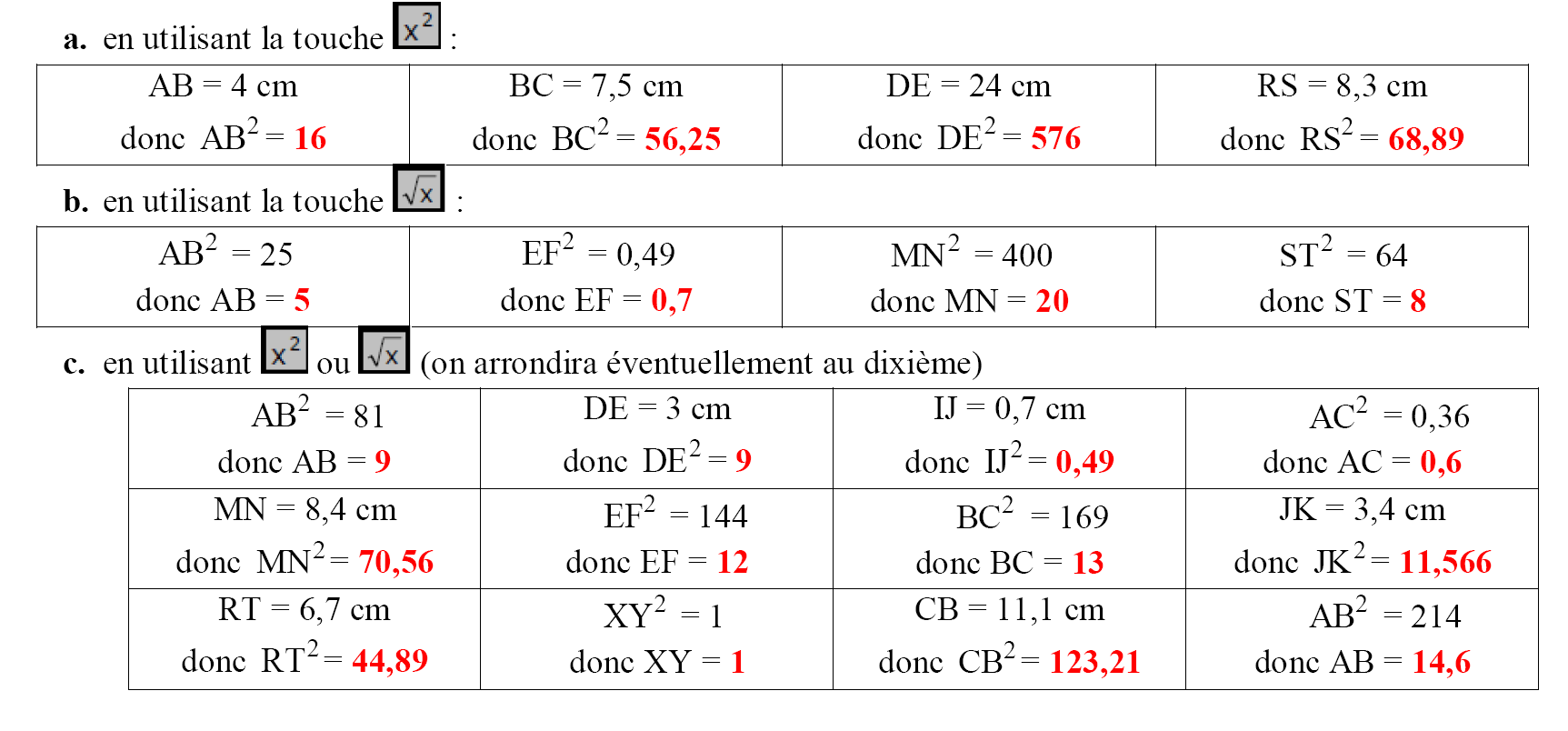
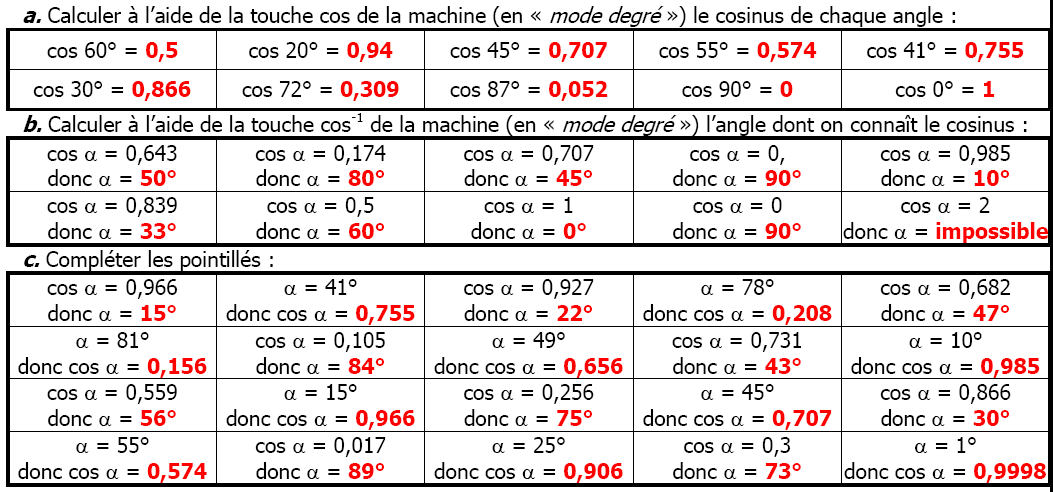
Théorème de Pythagore et cosinus d’un angle aigu exercices corrigés
Exercice 1:

Exercice 2:
Exercice 3:
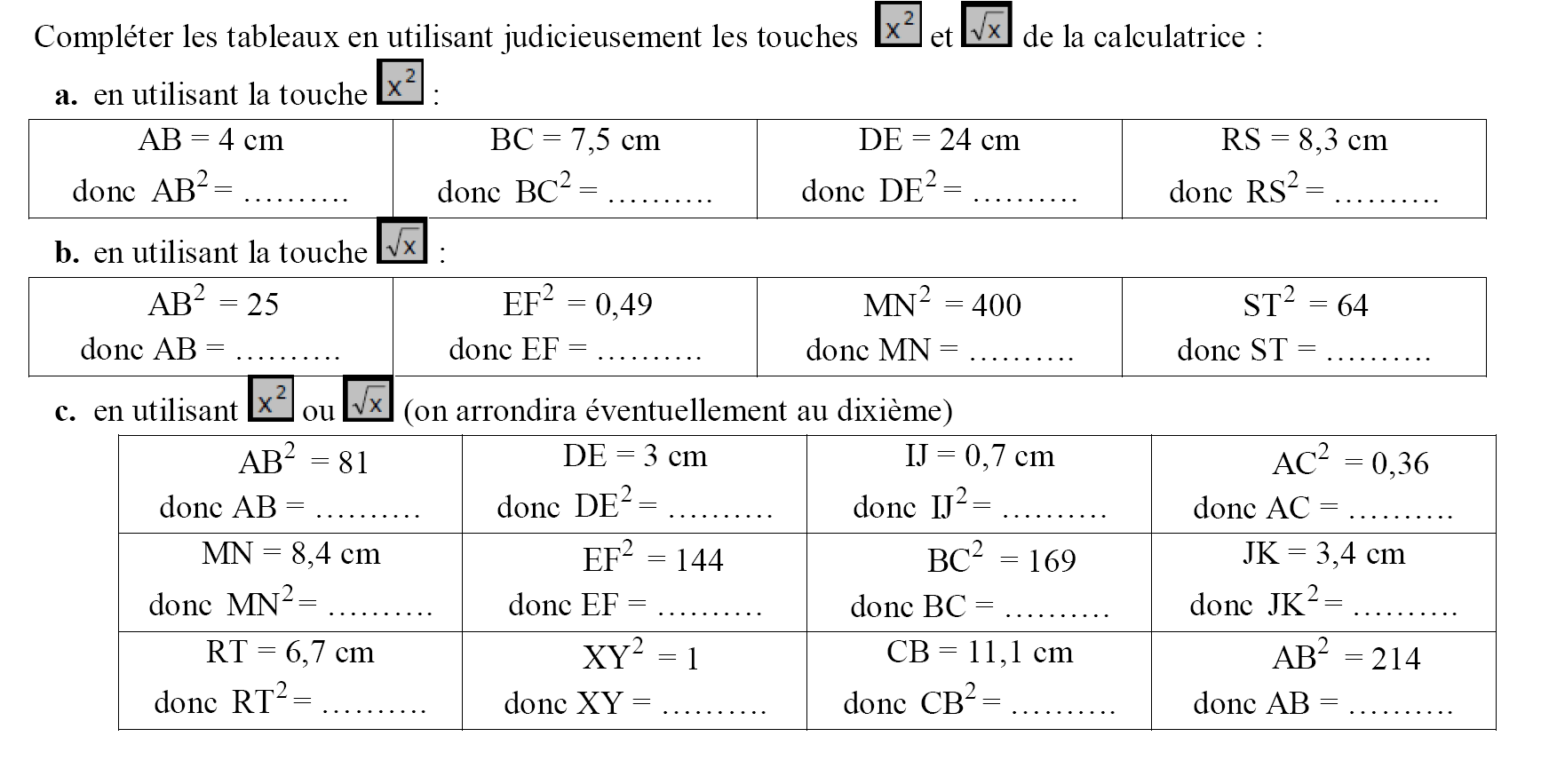
Exercice 4:
$1)$ $ABC$ est un triangle rectangle en $A$ tel que : $AB = 12 cm$ ; $AC = 16 cm$
• Calculer la longueur $BC$.
$2)$ ABC est un triangle tel que : $AB = 4,5 cm$ ; $AC = 2,7 cm$ ; $BC = 3,6 cm$
• Démontrer que $ABC$ est un triangle rectangle.
$3)$ $ LMN$ est un triangle rectangle en $L$ tel que : $LM = 6,8 cm$ ; $ MN = 6,89 cm$
• Calculer la longueur $LN$.
$4)$ $DEF$ est un triangle tel que : $DE = 15,3 cm$ ; $DF = 10,7 cm$ ; $EF = 18,2 cm$
• Ce triangle est-il rectangle ?
$5)$ $ABC$ est un triangle rectangle en $A$ tel que : $AB = 7,2 cm$ ; $BC = 15,3 cm$
• Calculer la longueur $ AC$.
$1)$ $A B C$ est un triangle rectangle en $A$ donc d’après le théorème de Pythagore:
$\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2}=12^{2}+16^{2}=144+256=400$
$\mathrm{BC}=\sqrt{400}=20 \mathrm{~cm}$
$2)$ Le plus grand côté est $[A B]$ : $A B^{2}=4,5^{2}=20,25$
$\mathrm{AC}^{2}+\mathrm{BC}^{2}=2,7^{2}+3,6^{2}=7,29+12,96=20,25$
Ainsi: $\mathrm{AB}^{2}=\mathrm{AC}^{2}+\mathrm{BC}^{2}$
D’après la réciproque du théorème de Pythagore : le triangle $A B C$ est rectangle en $C$.
$3)$ LMN est un triangle rectangle en $L$ donc d’après le théorème de Pythagore :
$\mathrm{MN}^{2}=\mathrm{LM}^{2}+\mathrm{LN}^{2} $ $\Leftrightarrow 6,89^{2}=6,8^{2}+\mathrm{LN}^{2} $
$ \Leftrightarrow 6,89^{2}-6,8^{2}=\mathrm{LN}^{2} $
$ \Leftrightarrow 1,2321=\mathrm{LN}^{2} $
$ \Leftrightarrow \mathrm{LN}=\sqrt{1,2321}=1,11$
$4)$ Le plus grand côté est $[EF]$ :
$\mathrm{EF}^{2}=18,2^{2}=331,24$ $\mathrm{DE}^{2}+\mathrm{DF}^{2}=15,3^{2}+10,7^{2}=234,09+114,49=348,58$
Ainsi : $\mathrm{EF}^{2} \neq \mathrm{DE}^{2}+\mathrm{DF}^{2}$
La réciproque du théorème de Pythagore ne $s^{\prime}$ applique pas : le triangle DEF n’est pas rectangle.
$5)$
$A B C$ est un triangle rectangle en $A$ donc d’après le théorème de Pythagore :
$\mathrm{BC}^{2}=\mathrm{AB}^{2}+\mathrm{AC}^{2} $$ $\Leftrightarrow 15,3^{2}=7,2^{2}+\mathrm{AC}^{2} $
$ \Leftrightarrow 15,3^{2}-7,2^{2}=\mathrm{AC}^{2} $
$ \Leftrightarrow 182,25=\mathrm{AC}^{2} $
$ \Leftrightarrow \mathrm{AC}=\sqrt{182,25}=13,5 \mathrm{~cm}$
Exercice 5:
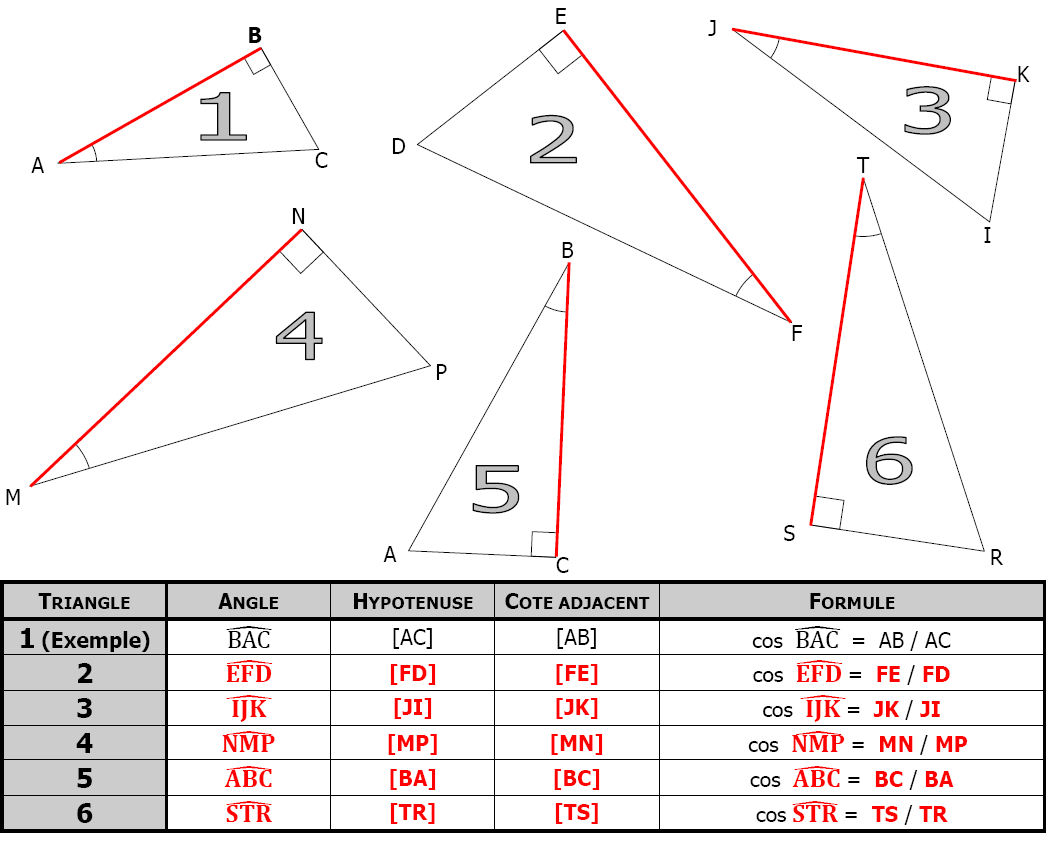
Identifier pour chaque triangle le coté adjacent à l’angle marqué d’un arc puis compléter le tableau.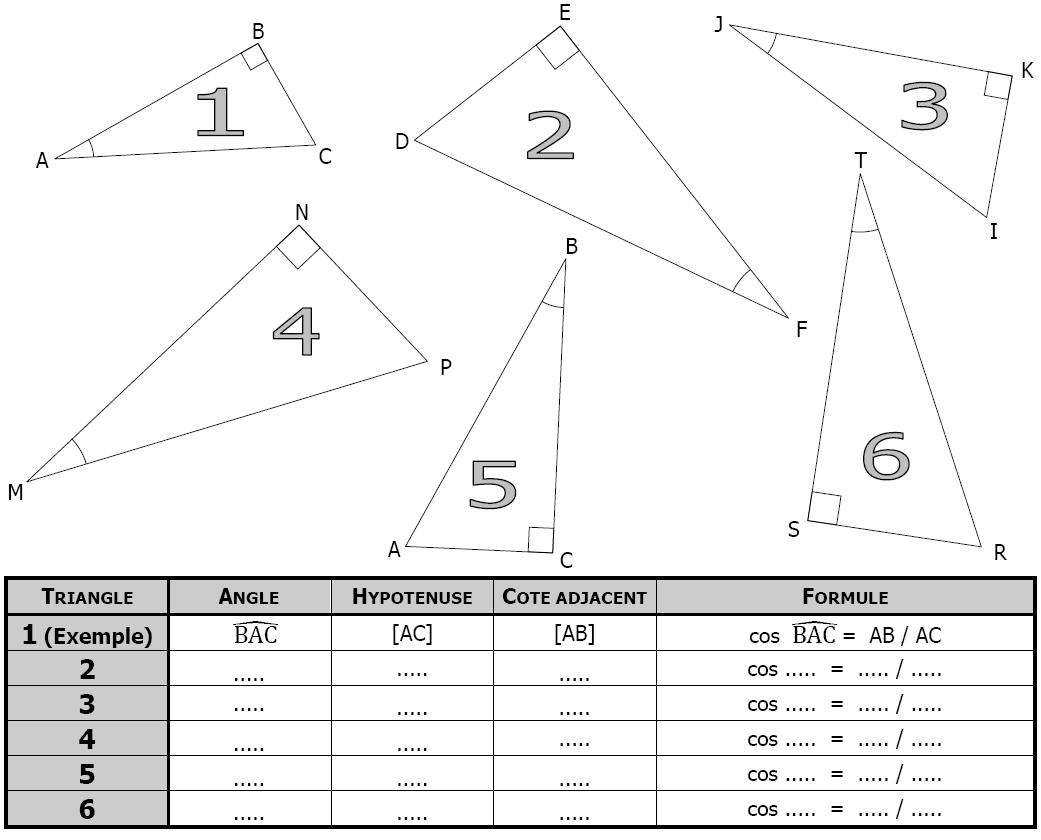
Exercice 6:
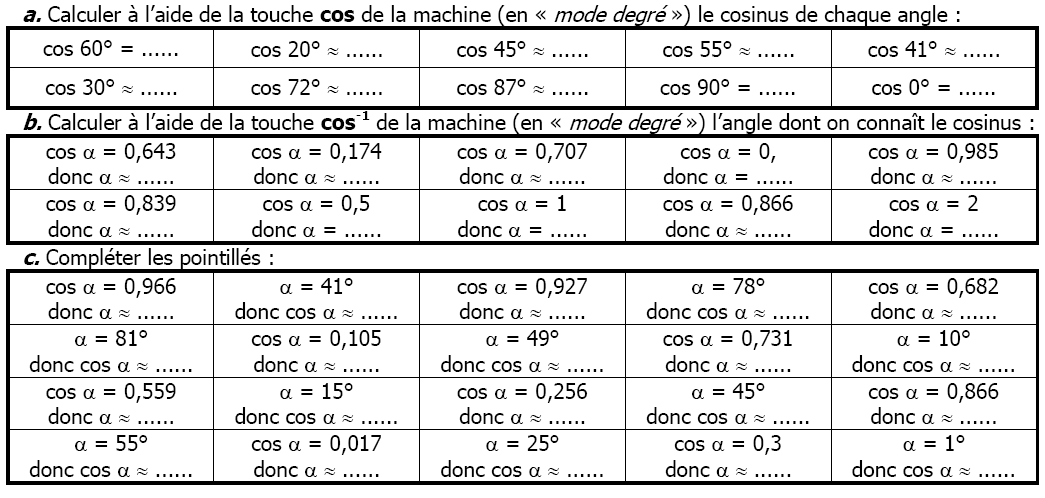
Exercice 7:
$1)$ $A B C$ est un triangle rectangle en $A$ tel que $A B=6 \mathrm{~cm}$ et $B C=7 \mathrm{~cm}$.
Calculer la mesure de l’angle $\widehat{A B C}$
$2)$ $IJK$ est un triangle rectangle en $I$ tel que $\mathrm{JK}=10 \mathrm{~cm}$ et $\widehat{\mathrm{IJK}}=55^{\circ}$.
Calculer la longueur de $[IJ]$
$3)$ $PQR$ est un triangle rectangle en $R$ tel que $\mathrm{PR}=45 \mathrm{~cm}$ et $\widehat{\mathrm{QPR}}=53^{\circ}$
Calculer la longueur de $[PQ]$
$1)$
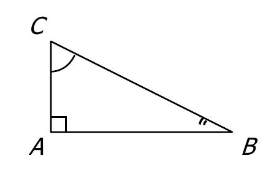
$ \cos \widehat{\mathrm{ABC}}=\frac{\mathrm{BA}}{\mathrm{BC}} $
$ \cos \widehat{\mathrm{ABC}}=\frac{6}{7} $
$ \cos \widehat{\mathrm{ABC}}=0,857$
$\widehat{\mathrm{ABC}} \approx 31^{\circ}$
$2)$
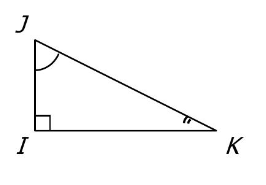
$\cos \sqrt{\mathrm{JK}}=\frac{\mathrm{JI}}{\mathrm{JK}}$
$\cos 55=\frac{\mathrm{JI}}{10}$
$0,574=\frac{\mathrm{JI}}{10}$
$0,574 \times 10=\mathrm{JI}$
$\mathrm{JI} \approx 5,7 \mathrm{~cm}$
$3)$
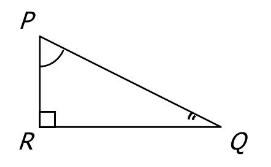
$\cos \widehat{\mathrm{QPR}}=\frac{\mathrm{PR}}{\mathrm{PQ}}$
$\cos 53=\frac{45}{P Q}$
$0,602=\frac{45}{P Q}$
$P Q=\frac{45}{0,602} \approx 74,8 \mathrm{~cm}$
Exercice 8:
$ABC$ est un triangle rectangle en $A$.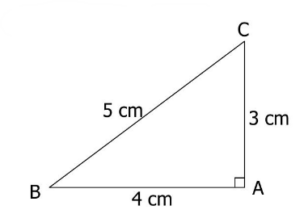
Calculer les mesures des angles $\widehat{A B C}$ et $\widehat{A C B}$ arrondies au degré prés.
$A B C$ est un triangle rectangle en $A$.
Calcul des mesures des angles $\widehat{A B C}$ et $\widehat{A C B}$
Calcul de l’angle $\widehat{A B C}$ :
$\cos \widehat{\mathrm{ABC}}=\frac{\mathrm{BA}}{\mathrm{BC}}$
$\cos \widehat{\mathrm{ABC}}=\frac{4}{5}$
$\cos \widehat{\mathrm{ABC}}=0,8$
$\widehat{\mathrm{ABC}} \approx 37^{\circ}$
Calcul de l’angle $\widehat{A C B}$ :
$ \cos \widehat{\mathrm{ACB}}=\frac{\mathrm{CA}}{\mathrm{BC}} $
$ \cos \widehat{\mathrm{ACB}}=\frac{3}{5}$
$ \cos \widehat{\mathrm{ACB}}=0,6 $
$ \widehat{\mathrm{ACB}} \approx 53^{\circ}$
Ou bien : on utilise la propriété: «La somme des angles d’un triangle vaut $180$‥”
$\widehat{\mathrm{ACB}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{CAB}}=180 $
$ \overline{\mathrm{ACB}}+37+90=180 $
$ \overline{\mathrm{ACB}}=180-90-37 $
$ \overline{\mathrm{ACB}}=53^{\circ}$
Exercice 9:
Calculer les mesures des $3$ angles de ce triangle :
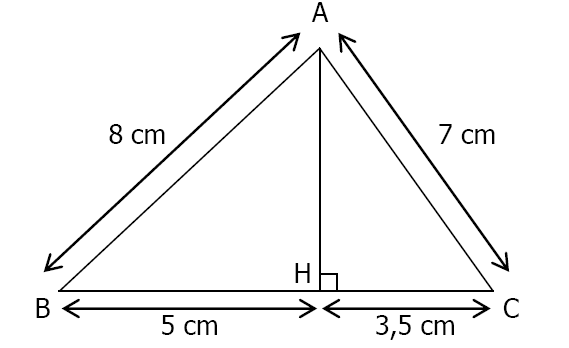
Calcul de l’angle $\widehat{A B C}$ :
Dans le triangle $A B H$, rectangle en $H$ , on a :
$ \cos \widehat{\mathrm{ABH}}=\frac{\mathrm{BH}}{\mathrm{BA}} $
$ \cos \widehat{\mathrm{ABH}}=\frac{5}{8} $
$ \cos \widehat{\mathrm{ABH}}=0,625 $
$ \widehat{\mathrm{ABH}} \approx 51^{\circ}$
Donc $\widehat{\mathrm{ABC}} \approx 51^{\circ}$
Calcul de l’angle $\widehat{A C B}$ :
Dans le triangle $ACH$ , rectangle en $H$ , on a :
$\cos \widehat{\mathrm{ACH}}=\frac{\mathrm{CH}}{\mathrm{CA}} $
$\cos \widehat{\mathrm{ACH}}=\frac{3,5}{6} $
$\cos \widehat{\mathrm{ACH}}=0,583 $
$\widehat{\mathrm{ACH}} \approx 54^{\circ} $
Donc : $ \overline{\mathrm{ACB}} \approx 54^{\circ}$
Calcul de l’angle $\widehat{B A C}$ :
D’après la propriété: < La somme des angles d’un triangle vaut $180^{\circ}$ », dans le triangle $A B C$, on a :
$\widehat{\mathrm{ACB}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{CAB}}=180 $
$ 54+51+\widehat{\mathrm{CAB}}=180 $
$ \widehat{\mathrm{CAB}}=180-54-51 $
$ \overline{\mathrm{CAB}}=75^{\circ}$
Exercice 10:
Calcul de la longueur de la diagonale $[AC]$ de ce losange: 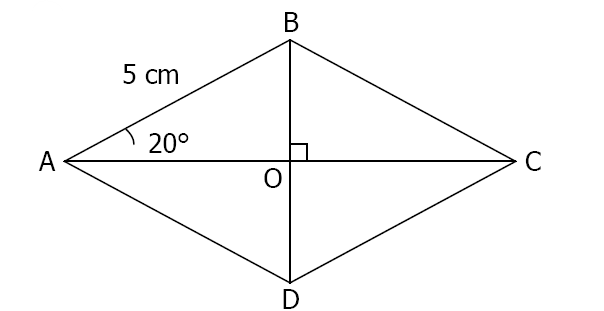
Calcul de la longueur de la diagonale $[AC]$ de ce losange:
$ABCD$ est un losange donc ses diagonales se coupent en leur milieu.}
Donc $0$ est le milieu de $[AC]$.
Autrement dit: $AC=2×AO$
Calcul de la longueur du segment $[AO]$:
Dans le triangle $ABO$, rectangle en $O$, on a :
$\cos \widehat{\mathrm{BAO}}=\frac{\mathrm{AO}}{\mathbf{A B}}$
$\cos 20=\frac{A O}{5}$
$0,94=\frac{\mathrm{AO}}{5}$
$0,94 \times 5=A O$
$A O \approx 4,7 \mathrm{~cm}$
• $A C =2 \times A O $
$\approx 2 \times 4,7$
$ \approx 9,4 \mathrm{~cm}$
Exercice 11:
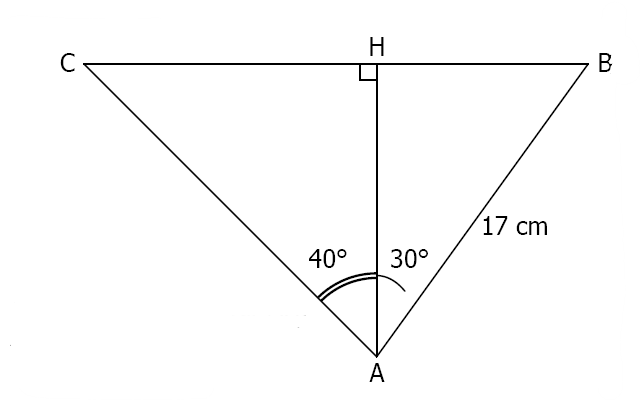
$1)$ Calculer la longueur $AH$
$2)$ Calculer la longueur $BH$
$3)$Calculer la longueur $AC$
$4)$Calculer la longueur $CH$.
[On arrondira les longueurs au $mm$]
$1)$ Calcul de la longueur $AH$.
Dans le triangle $A B H$, rectangle en $H$ , on a :
$\cos \widehat{\mathrm{HAB}}=\frac{\mathrm{AH}}{\mathbf{A B}}$
$\cos 30=\frac{\mathrm{AH}}{17}$
$0,866=\frac{\mathrm{AH}}{17}$
$0,866 \times 17=A H$
$A H \approx 14,7 \mathrm{~cm}$
$2)$ Calcul de la longueur $BH$ .
Dans le triangle $A B H$, rectangle en $H$, on a :
$\widehat{\mathrm{ABH}}=180-90-\mathbf{3 0}$
$\widehat{\mathrm{ABH}}=60^{\circ}$
$\cos \widehat{\mathrm{ABH}}=\frac{\mathrm{BH}}{\mathrm{BA}}$
$\cos 60=\frac{\mathrm{BH}}{17}$
$0,5=\frac{B H}{17}$
$0,5 \times 17=\mathrm{BH}$
$B H \approx 8,5 \mathrm{~cm}$
$3)$ Calculer la longueur $AC$.
Dans le triangle $ACH$ , rectangle en $H$ , on a :
$\cos \widehat{\mathrm{CAH}}=\frac{\mathrm{AH}}{\mathrm{AC}}$
$\cos 40=\frac{14,7}{A C}$
$0,766=\frac{14,7}{A C}$
$A C=\frac{14,7}{0,766} \approx 19,2 \mathrm{~cm}$
$4)$Calculer la longueur $CH$ .
Dans le triangle $ACH$ , rectangle en$ H$ , on a :
$\widehat{\mathrm{ACH}}=180-90-40$
$\widehat{\mathrm{ACH}}=50^{\circ}$
$\cos \widehat{\mathrm{ACH}}=\frac{\mathbf{C H}}{\mathbf{C A}}$
$\cos 50=\frac{C H}{19,2}$
$0,643=\frac{\mathrm{CH}}{19,2}$
$0,643 \times 19,2=\mathrm{CH}$
$C H \approx 12,3 \mathrm{~cm}$
Exercice 12:
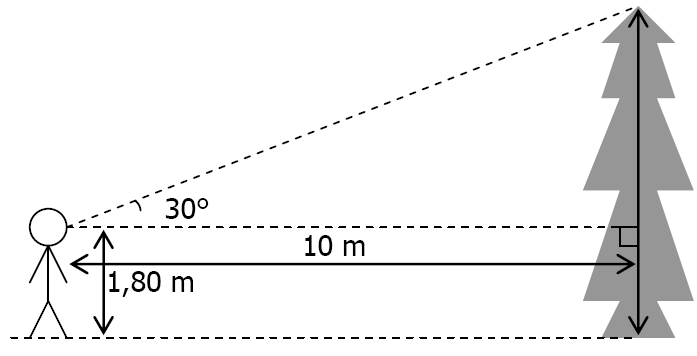
Un personnage mesurant $1,80 m$ se trouve à $10 m$ du pied d’un arbre. Alors qu’il regarde la cime, son regard fait un angle de $30°$ avec l’horizontale.
• Quelle est la hauteur de l’arbre (arrondie au $dm$)?
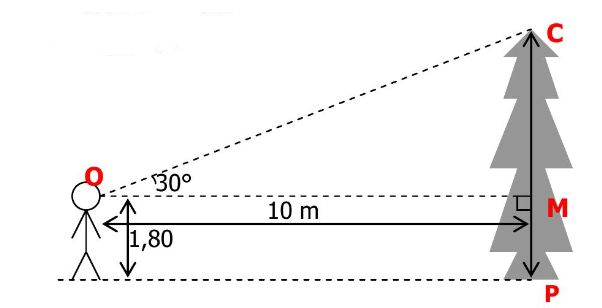
La hauteur de l’arbre est égale à la longueur $CP$.
$C P=C M+M P$
On sait que $M P=1,80 \mathrm{~m}$.
Calculons la longueur $CM$:
Dans le triangle $CMO$ rectangle en $M$ , on a :
$\cos \widehat{\mathrm{MCO}}=\frac{\mathbf{C M}}{\mathbf{C O}}$
$\widehat{M C O}=180-90-\widehat{\text { COM }}$
$\widehat{M C O}=180-90-30$
$\widehat{\mathrm{MCO}}=60^{\circ}$
D’où : $\quad \cos 60=\frac{C M}{C O}$
Pour calculer ainsi la longueur $CM$, on a donc besoin de connaître la longueur de l’hypoténuse, $CO$.
Calcul de $CO$ :
$\cos \widehat{\mathrm{MOC}}=\frac{\mathrm{OM}}{\mathrm{OC}}$
$\cos 30=\frac{10}{0 C}$
$0,866=\frac{10}{0 C}$
$O C=\frac{10}{0,866}$
$O C \approx 11,5 \mathrm{~m}$
On reprend alors le calcul de $CM$ :
$\cos 60=\frac{C M}{11,5}$
$0,5=\frac{C M}{11,5}$
$0,5 \times 11,5=C M$
$C M \approx 5,8 \mathrm{~m}$
Finalement : $C P \approx 5,8+1,8=\underline{7,6}$ mètres.
Théorème de Pythagore et cosinus d’un angle aigu exercices corrigés