Triangle rectangle et cercle des exercices corrigés
📐Exercice 1 :
Théorèmes du cercle circonscrit : Propriétés des triangles rectangles inscrits
$1)$ Si un triangle $ABC$ est rectangle en $A$ Alors $ABC$ est inscrit dans un demi-cercle de diamètre $[BC]$
Compléter les propriétés suivantes :
$a)$ Si un triangle $ABC$ est rectangle en $B$ Alors ……… est inscrit dans un demi-cercle de diamètre $[……]$
$b)$ Si un triangle $DEF$ est rectangle en $F$ Alors ……… est inscrit dans un demi-cercle de diamètre $[……]$
$2)$ Si $ABC$ est un triangle inscrit dans un demi-cercle de diamètre $[BC]$ Alors $ABC$ est rectangle en $A$
Compléter les propriétés suivantes :
$a)$ Si $ABC$ est un triangle inscrit dans un demi-cercle de diamètre $[AB]$ Alors ……. est rectangle en ….
$b)$ Si $DEF$ est un triangle inscrit dans un demi-cercle de diamètre $[DE]$ Alors ……. est rectangle en ….
$3)$ Si l’angle $BMC$ est droit Alors le point $M$ appartient au cercle de diamètre $[BC]$
Compléter les propriétés suivantes :
$a)$ Si l’angle $ABC$ est droit Alors le point ….. appartient au cercle de diamètre [……….]
$b)$ Si l’angle $EMF$ est droit Alors le point ….. appartient au cercle de diamètre [……….]
$4)$ Si un point $M$ appartient au cercle de diamètre $[BC]$ Alors l’angle $BMC$ est droit
Compléter les propriétés suivantes :
$a)$ Si un point $A$ appartient au cercle de diamètre $[IJ]$ Alors l’angle ………. est droit
$b)$ Si un point $C$ appartient au cercle de diamètre $[AB]$ Alors l’angle ………. est droit
$1)$ Si un triangle $ABC$ est rectangle en $A$ Alors $ABC$ est inscrit dans un demi-cercle de diamètre $[BC]$
Compléter les propriétés suivantes :
$a)$ Si un triangle $ABC$ est rectangle en $B$ Alors $ABC$ est inscrit dans un demi-cercle de diamètre $[AC]$
$b)$ Si un triangle $DEF$ est rectangle en $F$ Alors $DEF$ est inscrit dans un demi-cercle de diamètre $[DE]$
$2)$ Si $ABC$ est un triangle inscrit dans un demi-cercle de diamètre $[BC]$ Alors $ABC$ est rectangle en $A$
Compléter les propriétés suivantes :
$a)$ Si $ABC$ est un triangle inscrit dans un demi-cercle de diamètre $[AB]$ Alors $ABC$ est rectangle en $C$
$b)$ Si $DEF$ est un triangle inscrit dans un demi-cercle de diamètre $[DE]$ Alors $DEF$ est rectangle en $F$
$3)$ Si l’angle $BMC$ est droit Alors le point $M$ appartient au cercle de diamètre $[BC]$
Compléter les propriétés suivantes :
$a)$ Si l’angle $ABC$ est droit Alors le point $B$ appartient au cercle de diamètre $[AC]$
$b)$ Si l’angle $EMF$ est droit Alors le point $M$ appartient au cercle de diamètre $[EF]$
$4)$ Si un point $M$ appartient au cercle de diamètre $[BC]$ Alors l’angle $BMC$ est droit
Compléter les propriétés suivantes :
$a)$ Si un point $A$ appartient au cercle de diamètre $[IJ]$ Alors l’angle $IAJ$ est droit
$b)$ Si un point $C$ appartient au cercle de diamètre $[AB]$ Alors l’angle $ACB$ est droit
📐Exercice 2 :
🔍Construction et reconnaissance de triangles rectangles
$1)$ Sans tracer les médiatrices de ces $3$ triangles, construire leur cercle circonscrit :
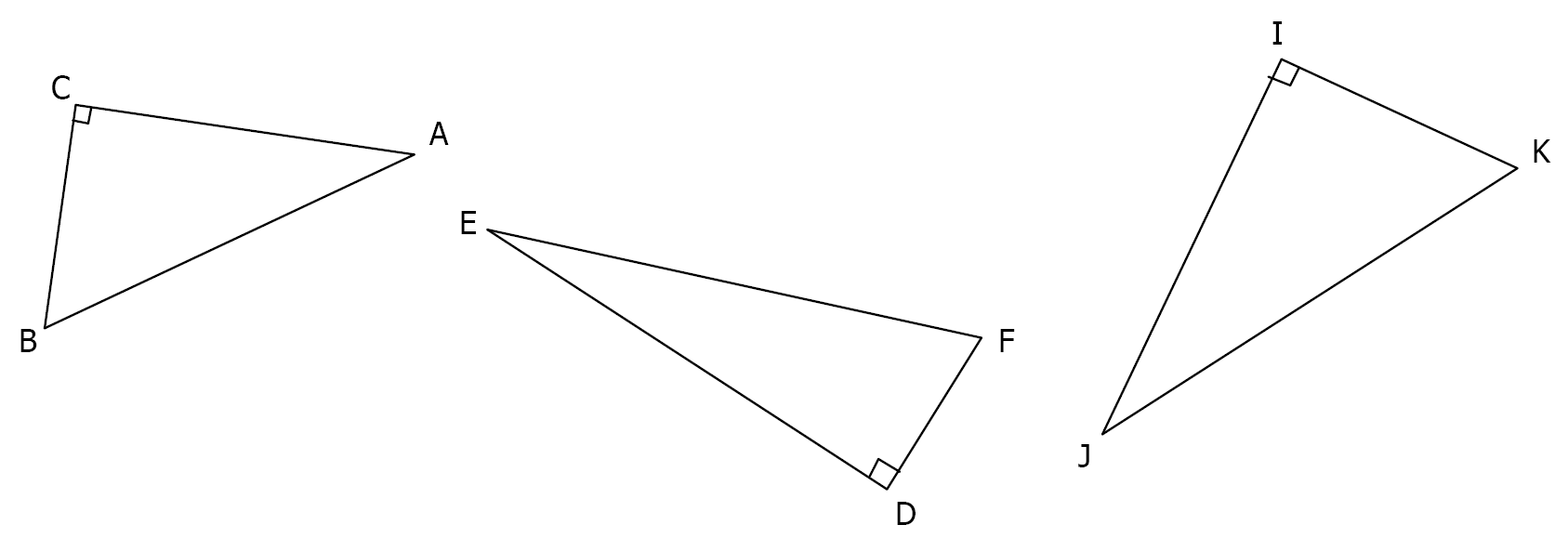
$2)$ Sans utiliser le moindre instrument de géométrie, les triangles suivants sont ils rectangles ?
($O$ est le centre du cercle).
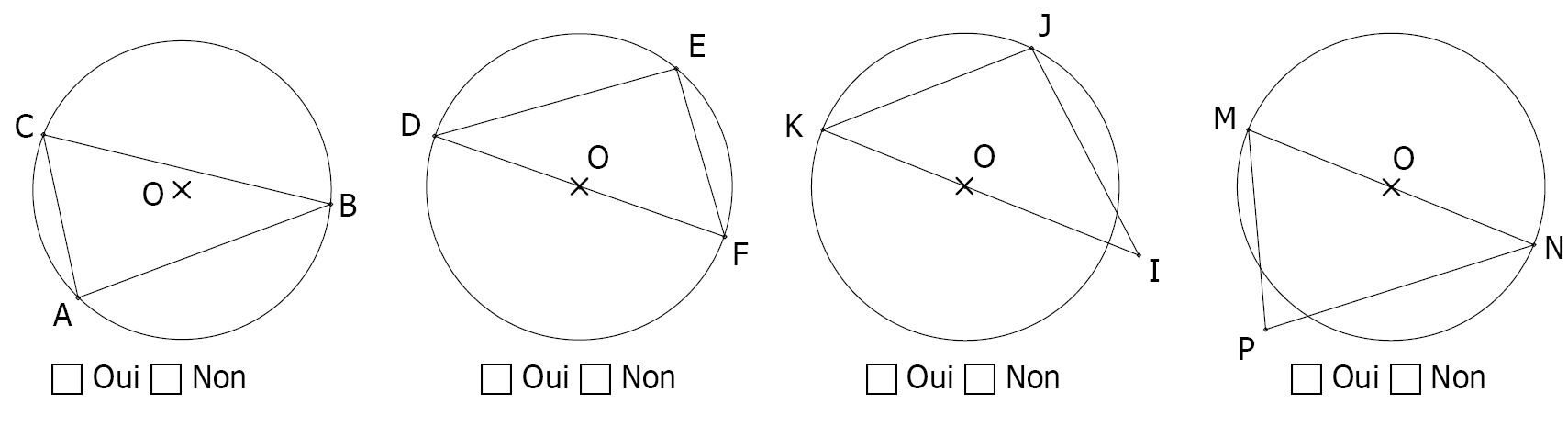
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 3 :
✏️Construction de triangles rectangles sans équerre
Sans utiliser l’équerre
$1)$ Construire un triangle $ABC$ rectangle en $C$ tel que $AB = 3 cm$.
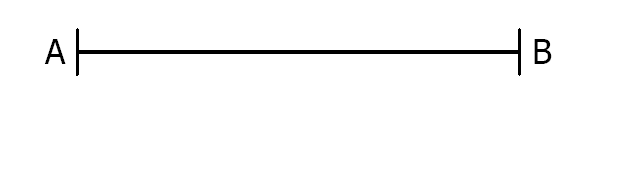
$2)$ Construire un triangle $DEF$ rectangle en $E$ tel que $\widehat{FDE}=45°$.
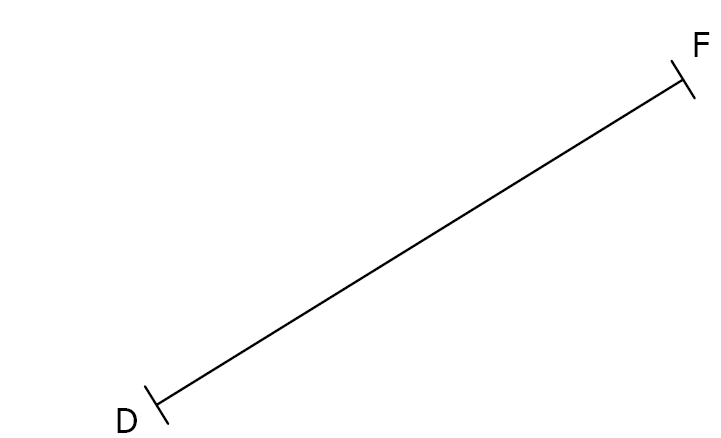
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 4 :
🎯Construction de points pour triangles rectangles multiples
Sans utiliser l’équerre…
$1)$ Construire le point $M$ tel que les triangles $ABM$ et $BCM$ soient rectangles en $M$.
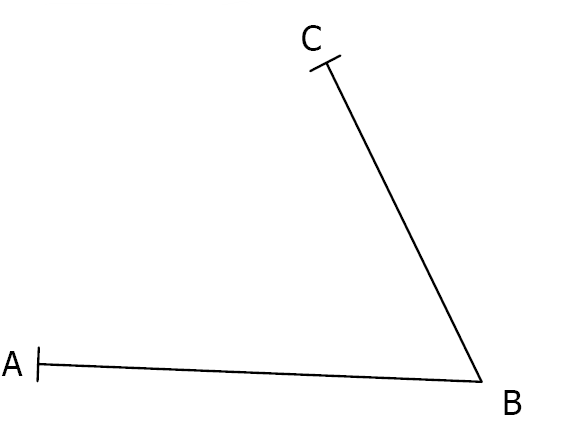
$2)$ Construire un point $M$ tel que les triangles $ABM$ et $CDM$ soient rectangles en $M$.
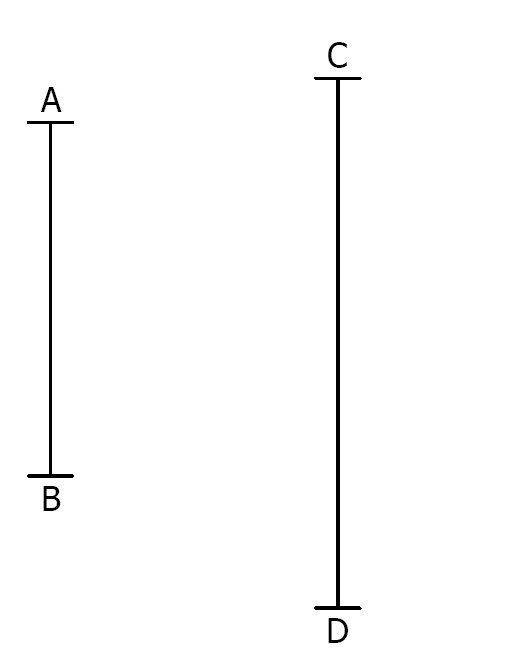
$3)$ Construire deux points $M$ et $N$ tels que les triangles $ABM, ABN, CDM$ et $CDN$ soient rectangles en $M$ et $N$.
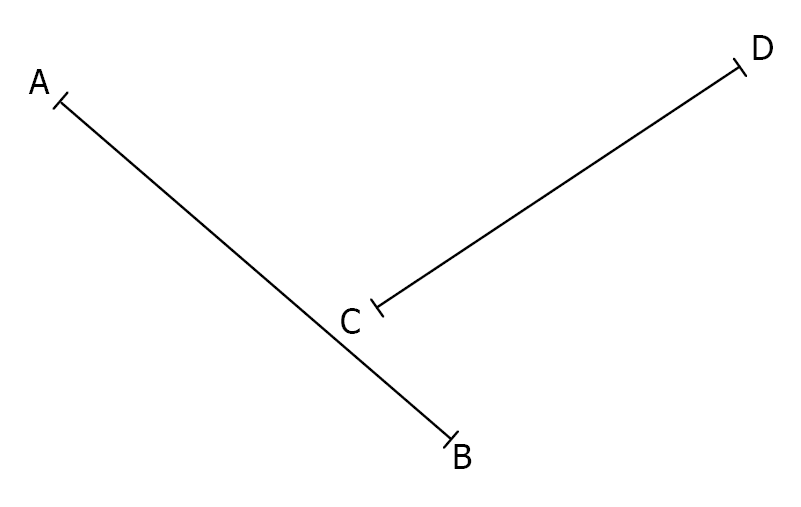
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 5 :
🔢Triangle rectangle et cercle circonscrit – Propriétés des longueurs
$ABC$ est un triangle rectangle en $A$, tel que $BC = 5 cm$. $O$ est le milieu de $[BC]$.

$1)$ Quel est le centre du cercle circonscrit à ce triangle (citer la propriété) ?
PUISQUE ………………………………………………………
ALORS …………………………………………………………
$2)$ En déduire l’égalité de $3$ longueurs :
……… = ……… = ………
$3)$ Combien mesure le segment $[AO]$ ? Expliquer.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 6 :
📏Triangle rectangle et propriété de la médiane
\(DEF\) est un triangle rectangle en \(E\). Le point \(I\) est le milieu de l’hypoténuse. La médiane \([EI]\) mesure \(5 cm\).
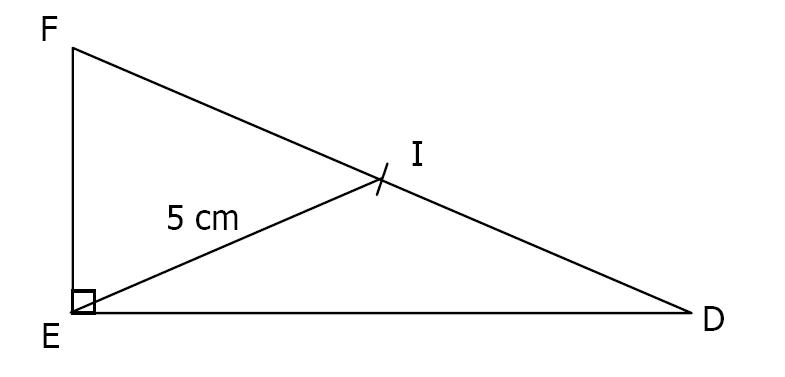
Combien mesure l’hypoténuse ? Expliquer.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 7 :
🔍Démonstration géométrique d’un triangle rectangle
\(O\) milieu de \([IJ]\) et \(K\) est tel que \(OK = OJ\).
Montrons que le triangle \(IJK\) est rectangle en \(K\).
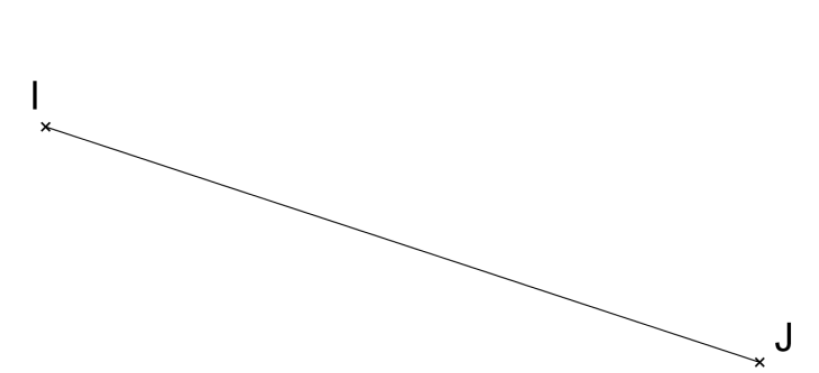
\(1)\) Placer les points \(O\) et \(K\).
\(2)\) Pourquoi les points \(I\), \(J\) et \(K\) appartiennent-ils au même cercle ?
\(3)\) Citer la caractérisation d’un triangle rectangle appliquée à cet énoncé.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 8 :
🧩Démonstration géométrique avec triangle isocèle et symétrie
\(DEF\) est un triangle isocèle en \(D\). \(E’\) est le symétrique de \(E\) par rapport à \(D\).
Démontrer que le triangle \(EFE’\) est rectangle en \(F\).
Conseil : Faire un schéma pour visualiser la situation. Penser aux propriétés de la symétrie centrale et des triangles isocèles.
📝 Démonstration à compléter :
Faire un schéma de la situation :
Énoncer les propriétés connues :
Développer le raisonnement :
Conclusion :
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 9 :
🎯Géométrie du cercle et triangles rectangles
\((C)\) est un cercle de centre \(O\). \(A\) et \(M\) sont deux points de \((C)\) non diamétralement opposés. La perpendiculaire en \(M\) à \((AM)\) recoupe \((C)\) en \(B\).
\(1)\) Faire une figure.
\(2)\) Démontrer que \(O\) est le milieu de \([AB]\).
\(3)\) \(N\) est un autre point du cercle \((C)\).
Démontrer que \(ANB\) est un triangle rectangle.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 10:
🎯Énoncé du problème
Considérons la figure ci-contre :
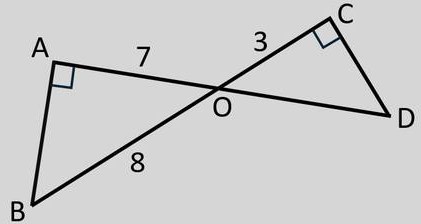
1) Calculer \( \cos \widehat{AOB} \)
2) Calculer OD.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 11:
🎯Énoncé du problème
Soit ABC un triangle équilatéral, et soit I le milieu de [BC].
1) Montrer que (AI) est la médiatrice de [BC].
2) En déduire la valeur de \( \cos 60^\circ \).
Rappel :
• Dans un triangle équilatéral, tous les côtés sont égaux et tous les angles mesurent \( 60^\circ \).
• La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 12:
🎯Énoncé du problème
Soit ABCD un parallélogramme de centre O. La droite qui passe par O et perpendiculaire à (AD) coupe (AD) et (BC) en I et J respectivement.
1) Construire une figure.
2) Montrer que \( \widehat{ODI} = \widehat{OBJ} \).
3) Montrer que \( BJ = DI \).
Rappel :
• Dans un parallélogramme, les diagonales se coupent en leur milieu.
• Les côtés opposés d’un parallélogramme sont parallèles et de même longueur.
🔒 Abonnez-vous pour accéder à la correction détaillée en texte et en vidéo.
📐Exercice 13:
🎯Énoncé du problème
Soit ABC un triangle rectangle en A, et soit H le projeté orthogonal de A sur (BC).
Montrer que \( AC^2 = CH \times BC \).
Rappel :
• Dans un triangle rectangle, le carré de la hauteur issue de l’angle droit est égal au produit des segments qu’elle détermine sur l’hypoténuse.
• Le projeté orthogonal d’un point sur une droite est le pied de la perpendiculaire menée de ce point à cette droite.
Triangle rectangle et cercle des exercices corrigés
