Triangles exercices corrigés 1AC
Exercice 1:
Compléter chacun des emplacements en pointillés.
$1)$ Si $BUS$ est un triangle isocèle en $U$ alors les deux côtés $[………]$ et $[………]$ issus du sommet $……………………..$ $U$ sont de même $……………………..$ et les deux angles $…………………….$ à sa base $[………]$ ont même $…………………..$ .
$2)$ Si un triangle $CAR$ est rectangle en $C$ alors le côté opposé à l’angle droit $[………]$ s’appelle $…………$ et les deux angles $……..$ et $……..$ sont $……………..$ .
$1)$ Si $BUS$ est un triangle isocèle en $U$ alors les deux côtés [$UB$] et [$US$] issus du sommet principal $U$ sont de même longueur et les deux angles adjacents à sa base [$BS$] ont même mesure.
$2)$ Si un triangle $CAR$ est rectangle en $C$ alors le côté opposé à l’angle droit [$AR$] s’appelle l’hypoténuse et les deux angles $\widehat{CAR}$ et $\widehat{CRA}$ sont complémentaires.
Exercice 2:
$1)$ Peut-on construire un triangle avec pour longueurs des côtés $7 cm, 11 cm$ et $2 cm$ ?
$2)$ $RS = 3 cm, ST = 4 cm$ et $RT = 7 cm$. Que peut-on dire des points $R, S$ et $T$ ?
Exercice 3:
Peut-on construire un triangle $DEF$ dans les cas suivants (en $cm$)?
$\begin{array} {|r|r|}\hline DE & DF & EF & Oui & Non \\ \hline 7 & 8 & 9 & & \\ \hline 3 & 2 & 6 & & \\ \hline 4,5 & 9,2 & 4,8 & & \\ \hline \end{array}$
Exercice 4:
Dans chacun des cas suivants, indiquer si les points $A, B$ et $C$ sont alignés.
Si $A, B$ et $C$ sont trois points tels que $𝑨𝑩 + 𝑩𝑪 = 𝐴𝐶$, alors le point $B$ appartient au segment $[AC]$. Autrement : les points$ A, B$ et $C$ sont alignés.
$\begin{array} {|r|r|}\hline AB & BC & CA & Alignés & Non \quad alignés \\ \hline 5 & 4 & 9 & & \\ \hline 3 & 4 & 1 & & \\ \hline 0,5 & 0,7 & 1,3 & & \\ \hline \end{array}$
Exercice 5:
Existe-t-il un triangle $ABC$ dont les angles sont les suivants ?
$\begin{array} {|r|r|}\hline \widehat{A} & \widehat{B} & \widehat{C} & Oui & Non \\ \hline 30^{\circ} & 60^{\circ} & 90^{\circ} & & \\ \hline 29^{\circ} & 41^{\circ} & 114^{\circ} & & \\ \hline 61^{\circ} & 79^{\circ} & 50^{\circ} & & \\ \hline \end{array}$
Exercice 6:
$1)$ $ABC$ est un triangle quelconque.
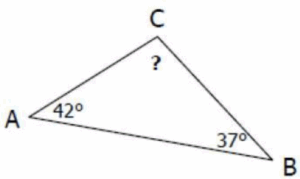
$a.$ Écrire l’égalité de la somme de ses $3$ angles.
$b.$ Remplacer dans cette égalité les angles qu’on connaît par leur valeur pour obtenir une équation.
$c.$ Résoudre l’équation pour obtenir la mesure de l’angle qui manquait.
$2)$ Calculer la mesure de l’angle $\widehat{F}$
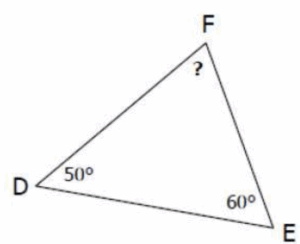
Exercice 7:
Retrouver mentalement la mesure de l’angle manquant de chaque triangle :
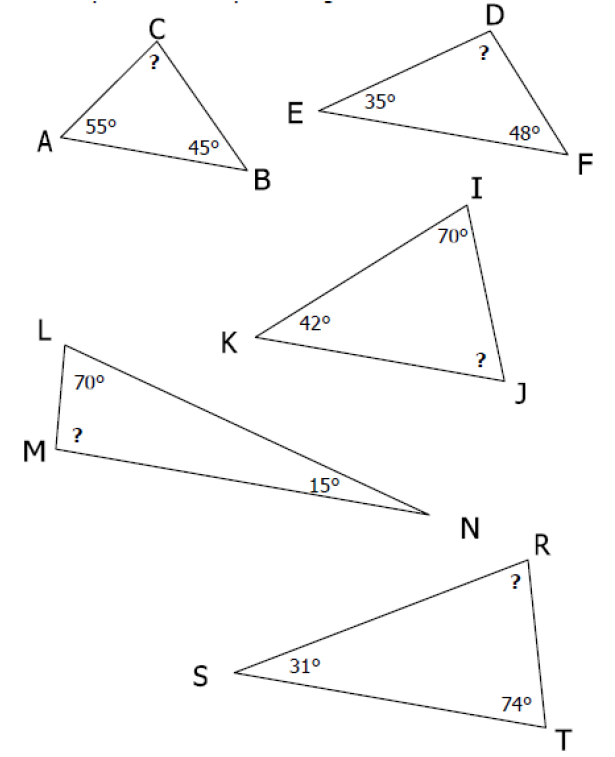
Exercice 8:
Construire un triangle $ABC$ répondant aux critères suivants :
$1)$ $AB = 7 cm, BC = 5 cm, AC = 10 cm$
$2)$ $AB = 9 cm, BC = 8,6 cm, AC = 7,5 cm$
$3)$ $AB = 3 cm, BC = 4 cm, AC = 7,5 cm$
$4)$ $ABC$ isocèle en $A$, $AB = 5 cm, BC = 7 cm$
$5)$ $ABC$ équilatéral, $BC = 6,5 cm$
Exercice 9:
Construire un triangle $DEF$ répondant aux critères suivants :
$1)$ $\widehat{D}= 50° $, $DE = 6 cm , DF = 9 cm$
$2)$ $\widehat{D}= 115°$ , $DE = 7,5 cm , DF = 10 cm$
$3)$ $\widehat{E}= 40° $, $DE = EF = 6 cm$
$4)$ $\widehat{F}= 90°$ , $FE = 4 cm , FD = 7 cm$
$5)$ $DEF$ est rectangle en $D$, $DE = 3 cm, DF = 4 cm$
Exercice 10:
$1)$ $\widehat{\mathrm{I}}=40^{\circ}, \widehat{\mathrm{J}}=70^{\circ}, \mathrm{IJ}=5 \mathrm{~cm}$
$2)$$\widehat{\mathrm{I}}=120^{\circ}, \quad \widehat{\mathrm{J}}=20^{\circ}, \quad \mathrm{IJ}=6 \mathrm{~cm}$
$3)$ $IJK$ est isocèle en $I$, $\widehat{\mathrm{J}}=40^{\circ}, \mathrm{IJ}=6 \mathrm{~cm}$
$4)$ $IJK$ est isocèle en $I$ , $\widehat{\mathrm{J}}=55^{\circ}, \quad \mathrm{JK}=10 \mathrm{~cm}$
$5)$ $IJK$ est isocèle en $I$, $\widehat{\mathrm{I}}=68^{\circ}, \mathrm{JK}=5 \mathrm{~cm}$
Exercice 11:
Retrouver mentalement la mesure de l’angle manquant de chaque triangle :
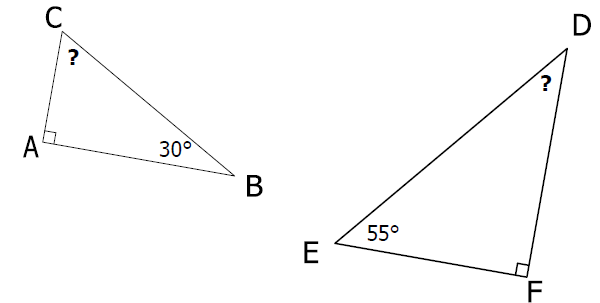
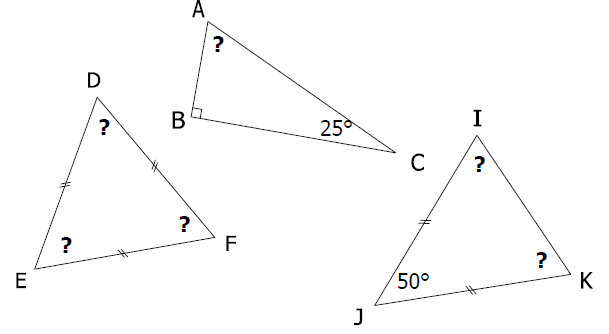
Exercice 12:
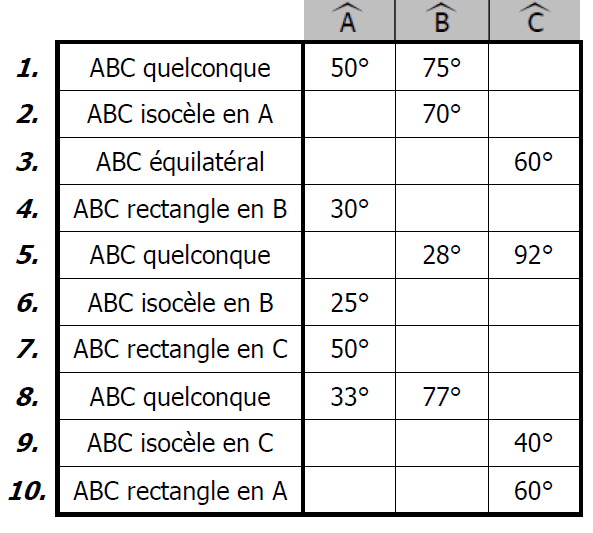
Retrouver les angles manquants de chaque triangle $ABC$.
Triangles exercices corrigés 1AC
