Trigonométrie
Exercice 1:
$1)$ Donner la mesure en radians de l’angle de mesure $30^{\circ}$.
$2)$ Donner la mesure en degrés de l’angle de mesure $\frac{3 \pi}{8} \mathrm{rad}$.
$3)$ Donner la mesure en radians de l’angle de mesure $135^{\circ}$.
$4)$ Donner la mesure en degrés de l’angle de mesure 1 rad
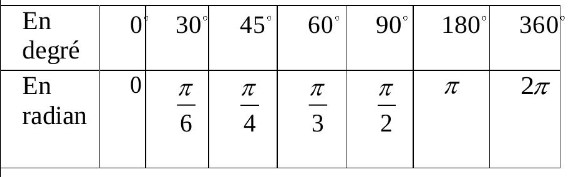
$5)$ Convertir en radians les mesures suivantes :
$0^{\circ} ; 30^{\circ} ; 45^{\circ} ; 60^{\circ} ; 90^{\circ} ; 180^{\circ} ; 360^{\circ}$
$1)$ $\frac{\alpha}{\pi}=\frac{\beta}{180}$ implique $\frac{\alpha}{\pi}=\frac{30}{180}$
C’est-à-dire : $\alpha=30 \times \frac{\pi}{180}=\frac{\pi}{6} \mathrm{rad}$.
$2)$ $\frac{\alpha}{\pi}=\frac{\beta}{180}$ implique $\frac{\alpha}{\pi}=\frac{\beta}{180}$
C’est-à-dire : $\alpha \times 180=\beta \times \pi$
$\beta=\frac{\alpha \times 180}{\pi}=\frac{3 \pi}{8} \times \frac{180}{\pi}=67,5^{\circ}$
$3)$ On a : $\frac{\alpha}{\pi}=\frac{\beta}{180}$ équivalent à : $\frac{\alpha}{\pi}=\frac{135}{180}$
Équivalent à : $\alpha=135 \times \frac{\pi}{180}=\frac{3 \pi}{4}$ rad.
$4)$ $\frac{\alpha}{\pi}=\frac{\beta}{180}$ équivalent à : $\frac{\alpha}{\pi}=\frac{\beta}{180}$
C’est-à-dire : $\alpha \times 180=\beta \times \pi$
$\beta=\frac{1 \times 180}{\pi}=\frac{180}{\pi}=57,29579143 \ldots \mathrm{deg} \simeq 57,2^{\circ}$
$5)$ De la même manière (on appliquant: $\frac{\alpha}{\pi}=\frac{\beta}{180}$ )
Nous obtenons les mesures remarquables que Résume le tableau suivant :
Exercice 2:
$1)$ Calculer la longueur L de l’arc $A B$ d’un cercle ( $C$ ) de rayon $R=3 \mathrm{~cm}$ et tel que : $\alpha=(\overline{A O B})=\frac{\pi}{3} \mathrm{rad}$
$2)$ Calculer la longueur L de l’arc $A B$ d’un cercle ( $C$ ) de rayon $R=60 \mathrm{~cm}$ et tel que : $\alpha=(\overline{A O B})=70 \mathrm{gr}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 3:
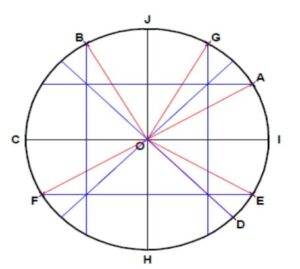
$1)$ Sur le cercle trigonométrique ci-contre, déterminer les abscisses curvilignes associés aux points : $A ; B ; C ; D ; E ; F ; G ; H ; I ; J$
$2)$ Déterminer l’abscisse curviligne principale de chacune des abscisses suivantes :
$7 \pi, \frac{110 \pi}{3}, \frac{19 \pi}{4},-\frac{131 \pi}{3},-\frac{217 \pi}{6}$
$3)$ Placer sur le cercle trigonométrique les points :
$A(0) ; B\left(\frac{\pi}{2}\right) ; C\left(\frac{\pi}{4}\right) ; D\left(\frac{\pi}{3}\right) ; E\left(\frac{\pi}{6}\right) ; M\left(\frac{7 \pi}{2}\right)$
$H\left(-\frac{\pi}{4}\right) ; G\left(-\frac{\pi}{2}\right) ; F\left(\frac{5 \pi}{6}\right) ; I_{I}\left(\frac{2007 \pi}{4}\right) ; N\left(\frac{3 \pi}{2}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 4:
Déterminer l’abscisse curviligne principale de chacune des points suivants:
$M_{0}\left(\frac{9 \pi}{2}\right) ; M_{1}\left(\frac{11 \pi}{3}\right) ; M_{2}\left(\frac{67 \pi}{4}\right) ; M_{3}\left(\frac{19 \pi}{3}\right)$;
$M_{4}\left(\frac{181 \pi}{6}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 5:
$1)$ Dans chacun des cas suivant, donner trois autres réels associés au même point sur le cercle trigonométrique :
$a)$ $A(-\pi)$
$b)$ $B\left(\frac{3 \pi}{2}\right)$
$c)$ $C(10 \pi)$
$d)$ $D\left(-\frac{\pi}{4}\right)$
$2)$ Parmi les mesures suivantes, indiquer celles qui sont associés au même point que : $M\left(-\frac{\pi}{12}\right)$ sur le cercle trigonométrique :
$\frac{47 \pi}{12} ; \frac{-49 \pi}{12} ; \frac{11 \pi}{12} ; \frac{-241 \pi}{12} ; \frac{-37 \pi}{12} ;-\frac{313 \pi}{12}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 6:
Soit sur un cercle trigonométrique d’origine $I$ les points $A ; B ; C ; D$ d’abscisses curvilignes respectifs : $\frac{85 \pi}{3} ; \frac{-139 \pi}{6} ; \frac{7 \pi}{4} ; \frac{11 \pi}{6}$.
$1)$ Placer sur le cercle trigonométrique ces points.
$2)$ En déduire les mesures des angles orientés : $(\overrightarrow{O I} ; \overrightarrow{O A}) ;(\overrightarrow{O I} ; \overrightarrow{O B}) ;(\overrightarrow{O A} ; \overrightarrow{O B}) ;(\overrightarrow{O I} ; \overrightarrow{O C})$; $(\overrightarrow{O I} ; \overrightarrow{O D})$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 7:
$A B C$ est un triangle rectangle en $A$ direct, tel que $(\overline{\overrightarrow{B A} ; \overrightarrow{B C}}) \equiv-\frac{\pi}{6}[2 \pi]$ et $A C D$ est un triangle équilatéral direct.
$1)$ Faire une figure.
$2)$ Déterminer la mesure principale des angles suivant :
$(\overrightarrow{A D} ; \overrightarrow{A B}) ;(\overrightarrow{D C} ; \overrightarrow{A C}) ;(\overrightarrow{D C} ; \overrightarrow{B A}) ;(\overrightarrow{C A} ; \overrightarrow{C B})$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 8:
Sachant que : $(\overline{\vec{u} ; \vec{v}}) \equiv-\frac{3 \pi}{4}[2 \pi]$
déterminer la mesure principale de : $(2 \vec{u} ; \vec{v}) ;(-\vec{v} ; 2 \vec{u}) ;(3 \vec{v} ;-2 \vec{u})$;
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 9:
Calculer les rapports trigonométriques des nombre réel suivants :
$7 \pi, \frac{5 \pi}{6}, \frac{7 \pi}{6}, \frac{3 \pi}{4},-\frac{4 \pi}{3} ;-\frac{35 \pi}{4}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 10:
Soit $-\pi<x<\pi$; calculer :
$A=\sin \left(\frac{6 \pi-x}{6}\right)+\sin \left(\frac{12 \pi+2 x}{12}\right) $
$B=\cos \left(\frac{5 \pi}{6}\right)+\sin \left(\frac{2 \pi}{3}\right)$
$C=\cos \left(\frac{14 \pi}{3}\right)+\sin \left(\frac{23 \pi}{6}\right)-2 \sin \left(\frac{9 \pi}{2}\right)$
$D=\cos \left(\frac{3 \pi}{4}\right) \times \sin \left(\frac{4 \pi}{3}\right) \times \cos \left(\frac{7 \pi}{6}\right) \times \sin \left(\frac{5 \pi}{4}\right) ;$
$E=\tan \left(\frac{2 \pi}{3}\right) \times \tan \left(\frac{5 \pi}{4}\right) \times \tan \left(\frac{5 \pi}{6}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 11:
Soit $-\pi<x<\pi$; calculer :
$\cos \frac{10 \pi}{3} ; \sin \frac{53 \pi}{6} ; \cos \frac{34 \pi}{3} ; \cos \frac{13 \pi}{6} ; \tan \frac{37 \pi}{4}$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 12:
$1)$ Montrer que : $1+\tan ^{2} x=\frac{1}{\cos ^{2} x}$ Si $: x \neq \frac{\pi}{2}+k \pi$
$2)$ On a : $\tan x=\frac{1}{3}$ et $\frac{\pi}{2}<x<\pi$
Calculer : $\cos x$ et $\sin x$
$3)$ On a : $\sin x=-\frac{4}{5}$ et $-\frac{\pi}{2}<x<\frac{\pi}{2}$
Calculer : $\cos x$ et $\tan x$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 13:
$1)$ Simplifier l’expression suivante :
$A(x)=\sin ^{2}\left(\frac{\pi}{2}-x\right)-\cos (-x+6 \pi)+\cos (3 \pi+x)+\sin \left(x-\frac{7 \pi}{2}\right)$
$2)$ Calculer $A\left(\frac{3 \pi}{4}\right)$ et $A\left(-\frac{10 \pi}{3}\right)$
$3)$$a)$ Calculer en fonction de $\sin x$ le nombre :
$A=\frac{\cos \left(\frac{3 \pi}{2}-x\right) \cos (4 \pi-x)}{\tan \left(\frac{3 \pi}{2}-x\right)}$
$b)$ En déduire la valeur de $A$ si $\tan x=3$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 14:
Simplifier les expressions suivantes :
$A=\sin (\pi-x) \times \cos \left(\frac{\pi}{2}-x\right)-\sin \left(\frac{\pi}{2}-x\right) \times \cos (\pi-x)$
$B=\frac{\sin x+\sin (\pi-x)}{\cos (\pi-x)}$
$C=\cos \left(\frac{5 \pi}{6}\right)+\sin \left(\frac{5 \pi}{6}\right)-\tan \left(\frac{5 \pi}{6}\right)$
$D=\sin (11 \pi-x)+\cos (5 \pi+x)+\cos (14 \pi-x)$
$E=\tan (\pi-x)+\tan (\pi+x)$
$F=\cos ^{2}\left(\frac{\pi}{5}\right)+\cos ^{2}\left(\frac{3 \pi}{10}\right)$
$G=\cos \left(\frac{\pi}{7}\right)+\cos \left(\frac{2 \pi}{7}\right)+\cos \left(\frac{3 \pi}{7}\right)+\cos \left(\frac{4 \pi}{7}\right)+\cos \left(\frac{5 \pi}{7}\right)+\cos \left(\frac{6 \pi}{7}\right)$
$H=\sin ^{2}\left(\frac{\pi}{8}\right)+\sin ^{2}\left(\frac{3 \pi}{8}\right)+\sin ^{2}\left(\frac{5 \pi}{8}\right)+\sin ^{2}\left(\frac{7 \pi}{8}\right)$
$K=\cos ^{2}\left(\frac{\pi}{10}\right)+\cos ^{2}\left(\frac{2 \pi}{10}\right)+\cos ^{2}\left(\frac{3 \pi}{10}\right)+\cos ^{2}\left(\frac{4 \pi}{10}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 15:
Simplifier et calculer les expressions suivantes:
$A=\cos (0)+\cos \left(\frac{\pi}{4}\right)+\cos \left(\frac{\pi}{2}\right)+\cos \left(3 \frac{\pi}{4}\right)+\cos (\pi)$
$B=\sin \left(\frac{\pi}{6}\right)+\sin \left(\frac{\pi}{3}\right)+\sin \left(\frac{\pi}{2}\right)+\sin \left(\frac{2 \pi}{3}\right)+\sin \left(\frac{5 \pi}{6}\right)+\sin (\pi)$
$C=\sin \left(\frac{11 \pi}{30}\right)-\sin \left(\frac{19 \pi}{30}\right)+\sin \left(\frac{11 \pi}{60}\right)-\cos \left(\frac{19 \pi}{60}\right)+\cos \left(\frac{11 \pi}{60}\right)-\sin \left(\frac{19 \pi}{60}\right)$
$D=\tan \left(\frac{\pi}{5}\right)+\tan \left(\frac{2 \pi}{5}\right)+\tan \left(\frac{3 \pi}{5}\right)+\tan \left(\frac{4 \pi}{5}\right)$
$E=\cos \left(\frac{\pi}{14}\right)+\cos \left(\frac{3 \pi}{14}\right)+\cos \left(\frac{5 \pi}{14}\right)+\cos \left(\frac{7 \pi}{14}\right)+\cos \left(\frac{9 \pi}{14}\right)+\cos \left(\frac{11 \pi}{14}\right)+\cos \left(\frac{13 \pi}{14}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Exercice 16:
Simplifier les expressions suivantes:
$A=\cos ^{2} \frac{\pi}{8}+\cos ^{2} \frac{3 \pi}{8}+\cos ^{2} \frac{7 \pi}{8}+\cos ^{2} \frac{5 \pi}{8}$
$B=\sin ^{2}\left(\frac{\pi}{12}\right)+\sin ^{2}\left(\frac{3 \pi}{12}\right)+\sin ^{2}\left(\frac{5 \pi}{12}\right)+\sin ^{2}\left(\frac{7 \pi}{12}\right)+\sin ^{2}\left(\frac{9 \pi}{12}\right)+\sin ^{2}\left(\frac{11 \pi}{12}\right)$
🔒 Abonnez-vous pour accéder à la correction détaillée en texte .
Trigonométrie
